Интегрирование произведения функций. Решение интегралов онлайн
В этой теме мы подробно поговорим вычислении неопределённых интегралов с помощью так называемой "формулы интегрирования по частям". Нам понадобится таблица неопределенных интегралов и таблица производных . В первой части будут разобраны стандартные примеры, которые большей частью встречаются в типовых расчётах и контрольных работах. Более сложные примеры разобраны во второй части .
Постановка задачи в стандартном случае следующая. Допустим, под интегралом у нас расположены две функции разной природы : многочлен и тригонометрическая функция, многочлен и логарифм, многочлен и обратная тригонометрическая функция и так далее. В этой ситуации выгодно отделить одну функцию от другой. Грубо говоря, имеет смысл разбить подынтегральное выражение на части, - и разобраться с каждой частью по отдельности. Отсюда и название: "интегрирование по частям". Применение этого метода основано на следующей теореме:
Пусть функции $u(x)$ и $v(x)$ дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл $\int v \; du$. Тогда на этом же промежутке существует и интеграл $\int u \; dv$, при этом верно следущее равенство:
\begin{equation} \int u \; dv=u\cdot v-\int v\; du \end{equation}
Формулу (1) и называют "формулой интегрирования по частям". Иногда, применяя вышеуказанную теорему, говорят о использовании "метода интегрирования по частям". Нам будет важна суть этого метода, которую и рассмотрим на примерах. Существует несколько стандартных случаев, в которых явно применима формула (1). Именно эти случаи и станут темой данной страницы. Пусть $P_n(x)$ - многочлен n-й степени. Введём два правила:
Правило №1
Для интегралов вида $\int P_n(x) \ln x \;dx$, $\int P_n(x) \arcsin x \;dx$, $\int P_n(x) \arccos x \;dx$, $\int P_n(x)\arctg x \;dx$, $\int P_n(x) \arcctg x \;dx$ принимаем $dv=P_n(x)dx$.
Правило №2
Для интегралов вида $\int P_n(x) a^x \;dx$ ($a$ - некоторое положительное число), $\int P_n(x) \sin x \;dx$, $\int P_n(x) \cos x \;dx$, $\int P_n(x)ch x \;dx$, $\int P_n(x) sh x \;dx$ принимаем $u=P_n(x)$.
Сразу отмечу, что указанные выше записи не нужно воспринимать буквально. Например, в интегралах вида $\int P_n(x) \ln x \;dx$ не обязательно будет стоять именно $\ln x$. Там могут быть расположены и $\ln 5x$, и $\ln (10x^2+14x-5)$. Т.е. запись $\ln x$ нужно воспринимать как своего рода обобщение.
Ещё один момент. Бывает, что формулу интегрирования по частям приходится применять несколько раз. Об этом поговорим подробнее в примерах №4 и №5. Теперь перейдём непосредственно к решению типичных задач. Решение задач, уровень которых чуть выше стандартных, разбирается во второй части .
Пример №1
Найти $\int (3x+4) \cos (2x-1) \; dx$.
Под интегралом расположен многочлен $3x+4$ и тригонометрическая функция $\cos (2x-1)$. Это классический случай для применения формулы , поэтому возьмём заданный интеграл по частям. Формула требует, чтобы интеграл $\int (3x+4) \cos (2x-1) \; dx$ был представлен в форме $\int u \; dv$. Нам нужно выбрать выражения для $u$ и для $dv$. Можно в качестве $u$ принять $3x+4$, тогда $dv=\cos (2x-1)dx$. Можно взять $u=\cos (2x-1)$, тогда $dv=(3x+4)dx$. Чтобы сделать правильный выбор обратимся к . Заданный интеграл $\int (3x+4) \cos (2x-1) \; dx$ подпадает под вид $\int P_n(x) \cos x \;dx$ (многочлен $P_n(x)$ в нашем интеграле имеет вид $3x+4$). Согласно нужно выбрать $u=P_n(x)$, т.е. в нашем случае $u=3x+4$. Так как $u=3x+4$, то $dv=\cos(2x-1)dx$.
Однако недостаточно просто выбрать $u$ и $dv$. Нам еще понадобятся значения $du$ и $v$. Так как $u=3x+4$, то:
$$ du=d(3x+4)=(3x+4)"dx=3dx.$$
Теперь разберёмся с функцией $v$. Так как $dv=\cos(2x-1)dx$, то согласно определению неопределённого интеграла имеем: $ v=\int \cos(2x-1)\; dx$. Чтобы найти нужный интеграл применим внесение под знак дифференциала :
$$ v=\int \cos(2x-1)\; dx=\frac{1}{2}\cdot \int \cos(2x-1)d(2x-1)=\frac{1}{2}\cdot \sin(2x-1)+C=\frac{\sin(2x-1)}{2}+C. $$
Однако нам нужно не всё бесконечное множество функций $v$, которое описывает формула $\frac{\sin(2x-1)}{2}+C$. Нам нужна какая-то одна функция из этого множества. Чтобы получить искомую функцию нужно вместо $C$ подставить какое-либо число. Проще всего, разумеется, подставить $C=0$, получив при этом $v=\frac{\sin(2x-1)}{2}$.
Итак, соберём всё вышеизложенное воедино. Мы имеем: $u=3x+4$, $du=3dx$, $dv=\cos(2x-1)dx$, $v=\frac{\sin(2x-1)}{2}$. Подставляя всё это в правую часть формулы будем иметь:
$$ \int (3x+4) \cos (2x-1) \; dx=(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx. $$
Осталось, по сути, только найти $\int\frac{\sin(2x-1)}{2}\cdot 3dx$. Вынося константу (т.е. $\frac{3}{2}$) за знак интеграла и применяя метод внесения под знак дифференциала , получим:
$$ (3x+4)\cdot \frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx= \\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\int \sin(2x-1) \;d(2x-1)= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C=\\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C. $$
Итак, $\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C$. В сокращенном виде процесс решения записывают так:
$$ \int (3x+4) \cos (2x-1) \; dx=\left | \begin{aligned} & u=3x+4; \; du=3xdx.\\ & dv=\cos(2x-1)dx; \; v=\frac{\sin(2x-1)}{2}. \end{aligned} \right |=\\ =(3x+4)\cdot\frac{\sin(2x-1)}{2}-\int \frac{\sin(2x-1)}{2}\cdot 3dx= \frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{2}\int \sin(2x-1) \;dx=\\ =\frac{(3x+4)\cdot\sin(2x-1)}{2}-\frac{3}{4}\cdot (-\cos (2x-1))+C= \frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C. $$
Неопределённый интеграл по частям найден, осталось лишь записать ответ.
Ответ : $\int (3x+4) \cos (2x-1) \; dx=\frac{(3x+4)\cdot\sin(2x-1)}{2}+\frac{3}{4}\cdot \cos (2x-1)+C$.
Полагаю, здесь не обойдётся без вопроса, поэтому попробую сформулировать его и дать ответ.
Почему мы приняли именно $u=3x+4$ и $dv=\cos(2x-1)dx$? Да, интеграл был решён. Но, может быть, если бы мы взяли $u=\cos (2x-1)$ и $dv=(3x+4)dx$ интеграл тоже был бы найден!
Нет, если принять $u=\cos (2x-1)$ и $dv=(3x+4)dx$, то ничего хорошего с этого не выйдет, - интеграл не упростится. Судите сами: если $u=\cos(2x-1)$, то $du=(\cos(2x-1))"dx=-2\sin(2x-1)dx$. Кроме того, так как $dv=(3x+4)dx$, то:
$$ v=\int (3x+4) \; dx=\frac{3x^2}{2}+4x+C.$$
Приняв $C=0$, получим $v=\frac{3x^2}{2}+4x$. Подставим теперь в формулу найденные значения $u$, $du$, $v$ и $dv$:
$$ \int (3x+4) \cos (2x-1) \; dx=\cos (2x-1)\cdot \left(\frac{3x^2}{2}+4x \right) - \int \left(\frac{3x^2}{2}+4x \right) \cdot (-2\sin(2x-1)dx)=\\ =\cos (2x-1)\cdot \left(\frac{3x^2}{2}+4x \right) +2\cdot\int \left(\frac{3x^2}{2}+4x \right) \sin(2x-1)\;dx $$
И к чему мы пришли? Мы пришли к интегралу $\int \left(\frac{3x^2}{2}+4x \right) \sin(2x-1)\;dx$, который явно сложнее нежели исходный интеграл $\int (3x+4) \cos (2x-1) \; dx$. Это говорит о том, что выбор $u$ и $dv$ был сделан неудачно. После применения формулы интегрирования по частям полученный интеграл должен быть проще исходного. Находя неопределенный интеграл по частям мы должны упрощать его, а не усложнять, поэтому если после применения формулы (1) интеграл усложнился, то выбор $u$ и $dv$ осуществлён некорректно.
Пример №2
Найти $\int (3x^4+4x-1) \ln 5x \; dx$.
Под интегралом расположен многочлен (т.е. $3x^4+4x-1$) и $\ln 5x$. Этот случай подпадает под , поэтому возьмём интеграл по частям. Заданный интеграл имеет такую же структуру, как и интеграл $\int P_n(x) \ln x\; dx$. Вновь, как и в примере №1, нам нужно выбрать какую-то часть подынтегрального выражения $(3x^4+4x-1) \ln 5x \; dx$ в качестве $u$, а какую-то часть - в качестве $dv$. Согласно , нужно выбрать $dv=P_n(x)dx$, т.е. в нашем случае $dv=(3x^4+4x-1)dx$. Если из выражения $(3x^4+4x-1) \ln 5x \; dx$ "изьять" $dv=(3x^4+4x-1)dx$, то останется $\ln 5x$ - это и будет функция $u$. Итак, $dv=(3x^4+4x-1)dx$, $u=\ln 5x$. Для применения формулы нам понадобятся также $du$ и $v$. Так как $u=\ln 5x$, то:
$$ du=d(\ln 5x)=(\ln 5x)"dx=\frac{1}{5x}\cdot 5 dx=\frac{1}{x}dx. $$
Теперь найдём функцию $v$. Так как $dv=(3x^4+4x-1)dx$, то:
$$ v=\int(3x^4+4x-1)\; dx=\frac{3x^5}{5}+2x^2-x+C. $$
Из всего найденного бесконечного множества функций $\frac{3x^5}{5}+2x^2-x+C$ нам нужно выбрать одну. А проще всего это сделать приняв $C=0$, т.е. $v=\frac{3x^5}{5}+2x^2-x$. Для применения формулы всё готово. Подставим в правую часть указанной формулы значения $u=\ln 5x$, $du=\frac{1}{x}dx$, $v=\frac{3x^5}{5}+2x^2-x$ и $dv=(3x^4+4x-1)dx$ будем иметь:
$$ \int (3x^4+4x-1) \ln 5x \; dx=\left | \begin{aligned} & u=\ln 5x; \; du=\frac{1}{x}dx.\\ & dv=(3x^4+4x-1)dx; \; v=\frac{3x^5}{5}+2x^2-x. \end{aligned} \right |=\\ =\ln 5x \cdot \left (\frac{3x^5}{5}+2x^2-x \right)-\int \left (\frac{3x^5}{5}+2x^2-x \right)\cdot \frac{1}{x}dx=\\ =\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x -\int \left (\frac{3x^4}{5}+2x-1 \right)dx=\\ =\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x - \left (\frac{3x^5}{25}+x^2-x \right)+C=\\ =\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x - \frac{3x^5}{25}-x^2+x+C. $$
Ответ : $\int (3x^4+4x-1) \ln 5x \; dx=\left (\frac{3x^5}{5}+2x^2-x \right)\cdot\ln 5x - \frac{3x^5}{25}-x^2+x+C$.
Пример №3
Найти $\int \arccos x \; dx$.
Этот интеграл имеет структуру $\int P_n(x) \arccos x \;dx$, подпадающую под . Понимаю, что сразу возникнет резонный вопрос: "а где в заданном интеграле $\int\arccos x \; dx$ спрятали многочлен $P_n(x)$? Там же нет никакого многочлена, только арккосинус и всё!". Однако на самом деле под интегралом расположен не только арккосинус. Я представлю интеграл $\int arccos x \; dx$ в таком виде: $\int 1\cdot\arccos x \; dx$. Согласитесь, что от домножения на единицу подынтегральное выражение не изменится. Вот эта единица и есть $P_n(x)$. Т.е. $dv=1\cdot dx=dx$. А в качестве $u$ (согласно ) принимаем $\arccos x$, т.е. $u=\arccos x$. Значения $du$ и $v$, кои учавствуют в формуле , найдём так же, как и в предыдущих примерах:
$$ du=(\arccos x)"dx=-\frac{1}{\sqrt{1-x^2}}dx;\\ v=\int 1\; dx=x+C. $$
Как и в предыдущих примерах, полагая $C=0$ получим $v=x$. Подставляя все найденные параметры в формулу , будем иметь следующее:
$$ \int \arccos x \; dx=\left | \begin{aligned} & u=\arccos x; \; du=-\frac{1}{\sqrt{1-x^2}}dx.\\ & dv=dx; \; v=x. \end{aligned} \right |=\\ =\arccos x \cdot x-\int x\cdot \left(-\frac{1}{\sqrt{1-x^2}}dx \right)= \arccos x \cdot x+\int \frac{xdx}{\sqrt{1-x^2}}=\\ =x\cdot\arccos x-\frac{1}{2}\cdot\int (1-x^2)^{-\frac{1}{2}}d(1-x^2)= =x\cdot\arccos x-\frac{1}{2}\cdot\frac{(1-x^2)^{\frac{1}{2}}}{\frac{1}{2}}+C=\\ =x\cdot\arccos x-\sqrt{1-x^2}+C. $$
Ответ : $\int\arccos x \; dx=x\cdot\arccos x-\sqrt{1-x^2}+C$.
Пример №4
Найти $\int (3x^2+x) e^{7x} \; dx$.
В этом примере формулу интегрирования по частям придётся применять два раза. Интеграл $\int (3x^2+x) e^{7x} \; dx$ имеет структуру $\int P_n(x) a^x \;dx$. В нашем случае $P_n(x)=3x^2+x$, $a=e$. Согласно имеем: $u=3x^2+x$. Соответственно, $dv=e^{7x}dx$.
$$ du=(3x^2+x)"=(6x+1)dx;\\ v=\int e^{7x}\;dx=\frac{1}{7}\cdot \int e^{7x}\;d(7x)=\frac{1}{7}\cdot e^{7x}+C=\frac{e^{7x}}{7}+C. $$
Опять-таки, как и в предыдущих примерах, полагая $C=0$, имеем: $v=\frac{e^{7x}}{7}$.
$$ \int (3x^2+x) e^{7x} \; dx=\left | \begin{aligned} & u=3x^2+x; \; du=(6x+1)dx.\\ & dv=e^{7x}dx; \; v=\frac{e^{7x}}{7}. \end{aligned} \right |=\\ =(3x^2+x)\cdot\frac{e^{7x}}{7}-\int \frac{e^{7x}}{7}\cdot (6x+1)dx= \frac{(3x^2+x)e^{7x}}{7}-\frac{1}{7}\cdot \int (6x+1) e^{7x}\;dx. $$
Мы пришли к интегралу $\int (6x+1) e^{7x}\;dx$, который вновь необходимо брать по частям. Приняв $u=6x+1$ и $dv=e^{7x}dx$ будем иметь:
$$ \frac{(3x^2+x)e^{7x}}{7}-\frac{1}{7}\cdot \int (6x+1) e^{7x}\;dx=\left | \begin{aligned} & u=6x+1; \; du=6dx.\\ & dv=e^{7x}dx; \; v=\frac{e^{7x}}{7}. \end{aligned} \right |=\\ =\frac{(3x^2+x)e^{7x}}{7}-\frac{1}{7}\cdot \left ((6x+1)\cdot\frac{e^{7x}}{7} - \int\frac{e^{7x}}{7}\cdot 6\;dx \right)=\\ =\frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6}{49}\cdot\int\ e^{7x}\;dx=\\ =\frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6}{49}\cdot\frac{e^{7x}}{7}+C=\\ =\frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6\; e^{7x}}{343}+C. $$
Полученный ответ можно и упростить, раскрыв скобки и перегруппировав слагаемые:
$$ \frac{(3x^2+x)e^{7x}}{7} -\frac{(6x+1)e^{7x}}{49} +\frac{6\; e^{7x}}{343}+C=e^{7x}\cdot \left(\frac{3x^2}{7}+\frac{x}{49}-\frac{1}{343} \right)+C. $$
Ответ : $\int (3x^2+x) e^{7x} \; dx=e^{7x}\cdot \left(\frac{3x^2}{7}+\frac{x}{49}-\frac{1}{343} \right)+C$.
Пример №5
Найти $\int (x^2+5)\sin(3x+1) \; dx$.
Здесь, как и в предыдущем примере, интегрирование по частям применяется дважды. Подробные пояснения были даны ранее, поэтому приведу только решение:
$$ \int (x^2+5)\sin(3x+1) \; dx=\left | \begin{aligned} & u=x^2+5; \; du=2xdx.\\ & dv=\sin(3x+1)dx; \; v=-\frac{\cos(3x+1)}{3}. \end{aligned} \right |=\\ =(x^2+5)\cdot \left(-\frac{\cos(3x+1)}{3} \right)-\int\left(-\frac{\cos(3x+1)}{3} \right)\cdot 2xdx=\\ = -\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2}{3}\int x\cos(3x+1)dx= \left | \begin{aligned} & u=x; \; du=dx.\\ & dv=\cos(3x+1)dx; \; v=\frac{\sin(3x+1)}{3}. \end{aligned} \right |=\\ =-\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2}{3}\cdot \left(x\cdot\frac{\sin(3x+1)}{3}-\int\frac{\sin(3x+1)}{3}dx \right)=\\ =-\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{2}{9}\cdot\int\sin(3x+1)dx=\\ =-\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{2}{9}\cdot \left(-\frac{\cos(3x+1)}{3}\right)+C=\\ = -\frac{(x^2+5)\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}+\frac{2\cos(3x+1)}{27}+C=\\ =-\frac{x^2\cdot\cos(3x+1)}{3}-\frac{5\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}+\frac{2\cos(3x+1)}{27}+C=\\ =-\frac{x^2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C. $$
Ответ : $\int (x^2+5)\sin(3x+1) \; dx=-\frac{x^2\cdot\cos(3x+1)}{3} +\frac{2x\sin(3x+1)}{9}-\frac{43\cos(3x+1)}{27}+C$.
Применение метода интегрирования по частям в несколько нестандартных случаях, не подпадающих под действие правил №1 и №2, будет дано во
Примеры интегрирования по частям подобного состава задают студентам 1, 2 курсов. Данные задания задавали на контрольной работе в ЛНУ им. И. Франка. Чтобы формулы в задачах и ответах не повторялись же задачи описывать не будем. По условию заданий нужно или "Найти интеграл", или "Вычислить интеграл".
Пример 8.
Интеграл находим по правилу интегрирования частями int(u*dv)=u*v-int(v*du).
Здесь главное правильно выбрать функции под правило. (Для себя запомните что за dv
если возможно выбирают периодические функции или такие, которые при дифференцировании с точностью до множителя дают сами себя - экспонента). В этом интеграле нужно синус внести под дифференциал
Дальнейшее интегрирование достаточно простое и на деталях останавливаться не будем.
Пример 9.
Снова нужно применять правило интегрирования по частям u*dv
. Здесь имеем произведение периодической функции на экспоненту, поэтому что лучше вносить под дифференциал выбирать Вам. Можно как экспоненту, так и косинус (в каждом варианте получим рекуррентную формулу). 
Применяем интегрирование по частям повторно
Пришли к рекуррентной формуле. Если записать интеграл который искали и результат вычислений то получим два подобные слагаемые
Группируем их и находим искомый интеграл
Пример 10.
Имеем готовую запись интеграла под правило u*dv.
Находим du
и выполняем интегрирование 
![]()
Сводим второй интеграл под табличную формулу и вычисляем его
Пример 11.
Обозначим за новую переменную cos(ln(x))=u
і найдем du
, затем внесением под дифференциал
![]()
К интегралу повторно применяем правило интегрирования по частям
Пришли к рекуррентной формуле
с которой и вычисляем неизвестный интеграл
Пример 12.
Для нахождения интеграла выделим в знаменателе полный квадрат. Далее сведя знаменатель к известной формуле интегрирования получим арктангенс

Хорошо запомните порядок чередования множителей. Единица разделена на корень из свободного члена фигурирует перед арктангенсом, также этот множитель присутствует в арктангенс перед переменной.
Пример 13.
Дело имеем с подобным интегралом, только в знаменателе квадратичная зависимость находится под корнем. Выделяем полный квадрат и сводим под формулу интегрирования, которая дает логарифм![]()
Вот такие бывают примеры на контрольной или тестах. Хорошо запомните основные схемы интегрирования.
Если не можете решить интеграл сами, тогда обращайтесь за помощью.
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) - F (a )).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
![]() (38)
(38)
Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
![]() (39)
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому

Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b , далее - значение нижнего предела a и вычисляется разность F(b) - F(a) . Полученное число и будет определённым интегралом. .
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
![]()
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
![]()
![]()
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
![]() (40)
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
![]()
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
![]() (41)
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
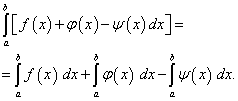 (42)
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
![]() (43)
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.
![]() (44)
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
![]() (45)
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
![]() (46)
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
![]()
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
![]() (47)
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
![]() (48)
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
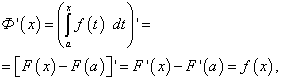
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
![]()
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна

Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.е.

Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:
F " (x) = f(x). (8.1)
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -
Если F(x) - какая-нибудь первобразная для функции f(x), то ∫ f(x)dx = F(x) + C, (8.2)
где С- произвольная постоянная.
Таблица интегралов
Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=const)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
Список табличных интегралов
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x /ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = arctg x + C
8. = arcsin x + C
10. = - ctg x + C
Замена переменной
Для интегрирования многих функций применяют метод замены переменной или подстановки, позволяющий приводить интегралы к табличной форме.
Если функция f(z) непрерывна на [α,β], функция z =g(x) имеет на непрерывную производную и α ≤ g(x) ≤ β, то
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
причем после интегрирования в правой части следует сделать подстановку z=g(x).
Для доказательства достаточно записать исходный интеграл в виде:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
Например:
Метод интегрирования по частям
Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные . Тогда, по произведения,
d(uv))= udv + vdu или udv = d(uv) - vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
∫ udv = uv - ∫ vdu (8.4.)
Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv"dx к интегрированию выражения vdu=vu"dx.
Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.
Определенный интеграл
Понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [
a,b] на n
частей точками a= x 0 < x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ
x i =x i - x i-1
. Сумма вида f(ξ i)Δ
x i называется интегральной суммой
, а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом
функции f(x) от a
до b
и обозначается:
F(ξ i)Δx i (8.5).
Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .
Для определенного интеграла справедливы следующие свойства:
4), (k = const, k∈R);
5)![]()
6)![]()
7) f(ξ)(b-a) (ξ∈).
Последнее свойство называется теоремой о среднем значении .
Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл
∫f(x)dx = F(x) + C
и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:
F(b) - F(a). (8.6)
Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox .
Несобственные интегралы
Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:
![]() (8.7)
(8.7)
Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится .
Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):
Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:
![]()
если эти пределы существуют и конечны. Обозначение:
Примеры вычисления интегралов
Пример 3.30. Вычислить ∫dx/(x+2).
Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .
Пример 3.31 . Найти ∫ tgxdx.
Решение. ∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Пример 3.32 . Найти ∫dx/sinxРешение.
Пример 3.33. Найти .
Решение. = .
Пример 3.34 . Найти ∫arctgxdx.
Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда
du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Пример 3.35 . Вычислить ∫lnxdx.
Решение.
Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Пример 3.36 . Вычислить ∫e x sinxdx.
Решение.
Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Интеграл
∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx,
du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Получили соотношение
∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, откуда 2∫e x sinx
dx = - e x cosx + e x sinx + С.
Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.
Решение. Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.
Пример 3.38 . Вычислить J = .
Решение.
Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = ![]() .
.
Пример
3.39
. Вычислить интеграл J = ![]() .
.
Решение.
Имеем: ![]() . Поэтому =
. Поэтому =
=
=.
вводится так sqrt(tan(x/2)).
А если в окне результата нажмете на Show steps в правом верхнем углу, то получите подробное решение.