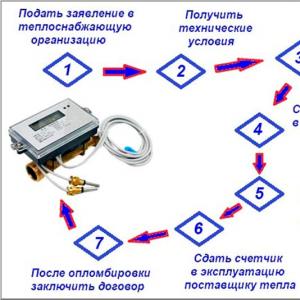
Хамгийн бага квадратын аргыг юунд ашигладаг вэ? Шугаман регресс. Хамгийн бага квадратын аргыг (LSM) ашиглах. MNC-ийн зарим хэрэглээ

• танилцуулах хичээл үнэ төлбөргүй байдаг;
• Олон тооны туршлагатай багш нар (төрөлх болон орос хэлтэй);
• Хичээлүүд тодорхой хугацаанд (сар, зургаан сар, жил) биш, харин тодорхой тооны хичээл (5, 10, 20, 50);
• 10,000 гаруй сэтгэл ханамжтай үйлчлүүлэгчид.
• Орос хэлтэй багштай нэг хичээлийн үнэ - 600 рубльээс, төрөлх хэлтэй - 1500 рубльээс

Хамгийн бага квадратын аргын мөн чанар нь зарим санамсаргүй үзэгдлийн хөгжлийн чиг хандлагыг цаг хугацаа, орон зайд хамгийн сайн дүрсэлсэн чиг хандлагын загварын параметрүүдийг олоход (трэнд гэдэг нь энэ хөгжлийн чиг хандлагыг тодорхойлсон шугам юм). Хамгийн бага квадратын аргын (OLS) даалгавар бол зөвхөн зарим чиг хандлагын загварыг олох биш, харин хамгийн сайн эсвэл оновчтой загварыг олох явдал юм. Хэрэв ажиглагдсан бодит утгууд ба холбогдох тооцоолсон чиг хандлагын утгуудын хоорондох квадрат хазайлтын нийлбэр хамгийн бага (хамгийн бага) байвал энэ загвар оновчтой байх болно.

ажиглагдсан бодит утгын хоорондох стандарт хазайлт хаана байна

болон харгалзах тооцоолсон чиг хандлагын утга,

Судалж буй үзэгдлийн бодит (ажиглагдсан) үнэ цэнэ,

Тренд загварын тооцоолсон үнэ цэнэ,

Судалж буй үзэгдлийн ажиглалтын тоо.

MNC-ийг дангаар нь ашиглах нь ховор. Дүрмээр бол энэ нь ихэвчлэн корреляцийн судалгаанд шаардлагатай арга хэрэгсэл болгон ашиглагддаг. LSM-ийн мэдээллийн үндэс нь зөвхөн найдвартай статистикийн цуврал байж болох бөгөөд ажиглалтын тоо 4-өөс багагүй байх ёстой гэдгийг санах нь зүйтэй, эс тэгвээс LSM-ийн жигдрүүлэх журам нь нийтлэг ойлголтоо алдаж болзошгүй юм.

OLS хэрэглүүрийг дараах журам болгон багасгасан.

Эхний процедур. Сонгогдсон хүчин зүйл-аргумент өөрчлөгдөхөд үр дүнгийн шинж чанарыг өөрчлөх хандлага байгаа эсэх, эсвэл өөрөөр хэлбэл " цагт "ба" X ».

Хоёр дахь журам. Энэ чиг хандлагыг аль шугам (траектор) хамгийн сайн дүрслэх эсвэл тодорхойлох чадвартай болохыг тодорхойлдог.

Гурав дахь журам.

Жишээ. Судалгаанд хамрагдаж буй фермийн наранцэцгийн дундаж ургацын талаарх мэдээлэл бидэнд байна гэж бодъё (Хүснэгт 9.1).

Хүснэгт 9.1

Ажиглалтын дугаар
Бүтээмж, ц/га

Манай улсын наранцэцгийн үйлдвэрлэлийн технологийн түвшин сүүлийн 10 гаруй жилд нэг их өөрчлөгдөөгүй тул дүн шинжилгээ хийсэн хугацаанд ургацын хэлбэлзэл нь цаг агаар, цаг уурын нөхцөл байдлын хэлбэлзлээс ихээхэн хамааралтай байсан гэсэн үг. Энэ үнэн үү?

MNC-ийн анхны процедур. Шинжилгээнд хамрагдсан 10 жилийн хугацаанд цаг агаар, цаг уурын өөрчлөлтөөс хамааран наранцэцгийн ургацын өөрчлөлтийн хандлага байгаа гэсэн таамаглалыг шалгаж байна.

Энэ жишээнд " y » наранцэцгийн ургацыг авах нь зүйтэй бөгөөд « x » нь дүн шинжилгээ хийсэн хугацаанд ажиглагдсан жилийн тоо юм. хооронд ямар нэгэн хамаарал байгаа тухай таамаглалыг шалгах нь " x "ба" y » гар аргаар болон компьютерийн программын тусламжтайгаар хоёр аргаар хийж болно. Мэдээжийн хэрэг, компьютерийн технологи бий болсноор энэ асуудал өөрөө шийдэгддэг. Гэхдээ OLS хэрэгслийн хэрэгслийг илүү сайн ойлгохын тулд "харилцан хамаарал байгаа" гэсэн таамаглалыг шалгахыг зөвлөж байна. x "ба" y » гарт зөвхөн үзэг болон энгийн тооны машин байгаа үед. Ийм тохиолдолд чиг хандлага байгаа гэсэн таамаглалыг дүн шинжилгээ хийсэн цаг хугацааны цувралын график дүрсийн байршлаар хамгийн сайн шалгадаг - корреляцийн талбар:

Бидний жишээн дэх корреляцийн талбар нь аажмаар нэмэгдэж буй шугамын эргэн тойронд байрладаг. Энэ нь өөрөө наранцэцгийн ургацын өөрчлөлтөд тодорхой чиг хандлага байгааг харуулж байна. Корреляцийн талбар нь тойрог, тойрог, хатуу босоо эсвэл хатуу хэвтээ үүл шиг харагдах эсвэл санамсаргүй тархсан цэгүүдээс бүрдэх үед л ямар нэгэн чиг хандлага байгаа талаар ярих боломжгүй юм. Бусад бүх тохиолдолд " хоорондын хамаарал байгаа гэсэн таамаглалыг батлах шаардлагатай. x "ба" y мөн судалгаагаа үргэлжлүүлнэ.

MNC-ийн хоёр дахь журам. Шинжилгээнд хамрагдсан хугацаанд наранцэцгийн ургацын өөрчлөлтийн чиг хандлагыг тодорхойлох эсвэл тодорхойлоход аль шугам (траектор) илүү сайн болохыг тодорхойлдог.

Компьютерийн технологи байгаа тул оновчтой чиг хандлагыг сонгох нь автоматаар явагддаг. "Гараар" боловсруулалт хийснээр оновчтой функцийг сонгохдоо дүрмээр бол харааны аргаар - корреляцийн талбайн байршлаар гүйцэтгэдэг. Өөрөөр хэлбэл, диаграмын төрлөөс хамааран эмпирик чиг хандлагад (бодит замнал руу) хамгийн тохиромжтой шугамын тэгшитгэлийг сонгоно.

Таны мэдэж байгаагаар байгальд маш олон янзын функциональ хамаарал байдаг тул тэдгээрийн өчүүхэн хэсгийг ч нүдээр шинжлэх нь маш хэцүү байдаг. Аз болоход эдийн засгийн бодит практикт ихэнх харилцааг парабол, гипербол, шулуун шугамаар нарийн тодорхойлж болно. Үүнтэй холбогдуулан хамгийн сайн функцийг сонгох "гарын авлагын" сонголтоор та зөвхөн эдгээр гурван загварт өөрийгөө хязгаарлаж болно.

		Гипербола:

Хоёрдахь эрэмбийн парабола: :

Бидний жишээн дээр дүн шинжилгээ хийсэн 10 жилийн хугацаанд наранцэцгийн ургацын өөрчлөлтийн чиг хандлага нь шулуун шугамаар хамгийн сайн тодорхойлогддог тул регрессийн тэгшитгэл нь шулуун шугамын тэгшитгэл байх болно гэдгийг харахад хялбар байдаг.

Гурав дахь журам. Энэ шугамыг тодорхойлсон регрессийн тэгшитгэлийн параметрүүдийг тооцоолж, өөрөөр хэлбэл хамгийн сайн чиг хандлагын загварыг тодорхойлсон аналитик томъёог тодорхойлно.

Регрессийн тэгшитгэлийн параметрүүдийн утгыг олох нь манай тохиолдолд ба параметрүүд нь LSM-ийн цөм юм. Энэ процессыг ердийн тэгшитгэлийн системийг шийдвэрлэх хүртэл багасгасан.

(9.2)

Энэ тэгшитгэлийн системийг Гауссын аргаар амархан шийддэг. Шийдлийн үр дүнд бидний жишээн дээр параметрийн утгууд олддог гэдгийг санаарай. Тиймээс олсон регрессийн тэгшитгэл нь дараах хэлбэртэй байна.

Бид функцийг 2-р зэргийн олон гишүүнтээр ойртуулна. Үүнийг хийхийн тулд бид ердийн тэгшитгэлийн системийн коэффициентийг тооцоолно.

, ,

Хамгийн бага квадратуудын ердийн системийг зохиоё, энэ нь дараах хэлбэртэй байна.

Системийн шийдлийг олоход хялбар:, , .

Ийнхүү 2-р зэргийн олон гишүүнт олдлоо: .

Онолын суурь

Хуудас руу буцах<Введение в вычислительную математику. Примеры>

Жишээ 2. Олон гишүүнтийн оновчтой зэрэглэлийг олох.

Хуудас руу буцах<Введение в вычислительную математику. Примеры>

Жишээ 3. Эмпирик хамаарлын параметрүүдийг олохын тулд хэвийн тэгшитгэлийн системийг гарган авах.

Коэффициент ба функцийг тодорхойлох тэгшитгэлийн системийг гаргаж авцгаая , энэ нь өгөгдсөн функцийн язгуурын квадратын ойролцооллыг цэгүүдийн хувьд гүйцэтгэдэг. Функц зохиох шаардлагатай экстремум нөхцөлийг бичнэ үү:

Дараа нь ердийн систем дараах хэлбэрийг авна.

Бид үл мэдэгдэх параметрүүдийн шугаман тэгшитгэлийн системийг олж авсан бөгөөд үүнийг амархан шийддэг.

Онолын суурь

Хуудас руу буцах<Введение в вычислительную математику. Примеры>

Жишээ.

Хувьсагчийн утгын туршилтын өгөгдөл Xболон цагтхүснэгтэд өгөгдсөн.

Тэдний тохируулгын үр дүнд функц

Ашиглаж байна хамгийн бага квадрат арга, эдгээр өгөгдлийг шугаман хамаарлаар ойролцоол y=ax+b(параметрүүдийг олох аболон б). Туршилтын өгөгдлүүдийг зэрэгцүүлж байгаа хоёр мөрийн аль нь илүү дээр болохыг олж мэд (хамгийн бага квадратын аргын утгаараа). Зураг зурах.

Хамгийн бага квадратын аргын мөн чанар (LSM).

Асуудал нь хоёр хувьсагчийн функцийг гүйцэтгэх шугаман хамаарлын коэффициентийг олох явдал юм аболон бхамгийн бага утгыг авдаг. Энэ нь өгөгдлийг өгсөн гэсэн үг юм аболон болсон шулуун шугамаас туршилтын өгөгдлийн квадрат хазайлтын нийлбэр хамгийн бага байх болно. Энэ бол хамгийн бага квадратын аргын бүх санаа юм.

Ийнхүү жишээний шийдэл нь хоёр хувьсагчийн функцийн экстремумыг олох хүртэл буурдаг.

Коэффициент олох томьёо гарган авах.

Хоёр үл мэдэгдэх хоёр тэгшитгэлийн системийг эмхэтгэж, шийддэг. Функцийн хэсэгчилсэн деривативуудыг олох хувьсагчаар аболон б, бид эдгээр деривативуудыг тэгтэй тэнцүүлж байна.

Бид үүссэн тэгшитгэлийн системийг ямар ч аргаар шийддэг (жишээлбэл орлуулах аргаэсвэл Крамерын арга) ба хамгийн бага квадратын арга (LSM) ашиглан коэффициентийг олох томъёог олж авна.

Өгөгдлийн хамт аболон бфункц хамгийн бага утгыг авдаг. Энэ баримтын нотолгоог хуудасны төгсгөлд байгаа текстэнд доор харуулав.

Энэ бол хамгийн бага квадратуудын бүх арга юм. Параметрийг олох томъёо анийлбэр, , , параметрийг агуулна nтуршилтын өгөгдлийн хэмжээ юм. Эдгээр дүнгийн утгыг тусад нь тооцоолохыг зөвлөж байна.

Коэффицент бтооцооны дараа олдсон а.

Анхны жишээг санах цаг болжээ.

Шийдэл.

Бидний жишээнд n=5. Шаардлагатай коэффициентүүдийн томъёонд орсон дүнг тооцоолоход хялбар болгох үүднээс бид хүснэгтийг бөглөнө.

Хүснэгтийн дөрөв дэх эгнээний утгыг тоо бүрийн 2-р эгнээний утгыг 3-р эгнээний утгуудаар үржүүлэх замаар олж авна. би.

Хүснэгтийн тав дахь эгнээний утгыг тоо тус бүрийн 2-р эгнээний утгыг квадрат болгох замаар олж авна. би.

Хүснэгтийн сүүлчийн баганын утгууд нь мөр хоорондын утгуудын нийлбэр юм.

Коэффициентийг олохын тулд бид хамгийн бага квадратын аргын томъёог ашигладаг аболон б. Бид тэдгээрт хүснэгтийн сүүлчийн баганаас харгалзах утгуудыг орлуулна.

Үүний үр дүнд, у=0,165х+2,184нь хүссэн ойролцоох шулуун шугам юм.

Аль мөрийг нь олж мэдэх л үлдлээ у=0,165х+2,184эсвэл анхны өгөгдөлд илүү ойртох, өөрөөр хэлбэл хамгийн бага квадратын аргыг ашиглан тооцоолол хийх.

Хамгийн бага квадратын аргын алдааны тооцоо.

Үүнийг хийхийн тулд та эдгээр мөрүүдээс анхны өгөгдлийн квадрат хазайлтын нийлбэрийг тооцоолох хэрэгтэй болон , жижиг утга нь хамгийн бага квадратын аргын хувьд анхны өгөгдөлд илүү сайн ойртсон шугамтай тохирч байна.

оноос хойш, дараа нь шугам у=0,165х+2,184анхны өгөгдлийг илүү ойртуулдаг.

Хамгийн бага квадратын аргын (LSM) график дүрслэл.

График дээр бүх зүйл сайхан харагдаж байна. Улаан шугам нь олсон шугам юм у=0,165х+2,184, цэнхэр шугам нь , ягаан цэгүүд нь анхны өгөгдөл юм.

Энэ нь юунд зориулагдсан бэ, энэ бүх ойролцоо тооцоолол юунд зориулагдсан бэ?

Би хувьдаа өгөгдлийг тэгшитгэх, интерполяци, экстраполяцийн асуудлыг шийдвэрлэхэд ашигладаг (анхны жишээнд танаас ажиглагдсан утгын утгыг олохыг хүсч болно. yцагт x=3эсвэл хэзээ x=6 MNC аргын дагуу). Гэхдээ бид энэ талаар дараа нь сайтын өөр хэсэгт дэлгэрэнгүй ярих болно.

Хуудасны дээд талд

Баталгаа.

Тиймээс олдсон үед аболон бфункц нь хамгийн бага утгыг авдаг тул энэ үед функцийн хоёр дахь эрэмбийн дифференциалын квадрат хэлбэрийн матриц шаардлагатай. эерэг тодорхой байсан. Үүнийг үзүүлье.

Хоёрдахь эрэмбийн дифференциал нь дараах хэлбэртэй байна.

Тэр бол

Тиймээс квадрат хэлбэрийн матриц нь хэлбэртэй байна

мөн элементүүдийн утга нь үүнээс хамаардаггүй аболон б.

Матриц нь эерэг тодорхой гэдгийг харуулъя. Энэ нь насанд хүрээгүй өнцөг нь эерэг байхыг шаарддаг.

Нэгдүгээр эрэмбийн өнцгийн минор . Оноонууд нь давхцдаггүй тул тэгш бус байдал нь хатуу байна. Үүнийг дараахь зүйлд тусгасан болно.

Хоёрдахь эрэмбийн өнцгийн минор

Үүнийг баталцгаая Математик индукцийн арга.

Дүгнэлт: олсон утгууд аболон бфункцийн хамгийн бага утгатай тохирно , тиймээс хамгийн бага квадратын аргын хүссэн параметрүүд юм.

Ойлгосон уу?
Шийдэл захиалах

Хуудасны дээд талд

Хамгийн бага квадратын аргыг ашиглан таамаглал боловсруулах. Асуудлыг шийдэх жишээ

Экстраполяци - энэ бол өмнөх болон одоогийн чиг хандлага, хэв маяг, урьдчилан таамаглах объектын ирээдүйн хөгжилд хамаарах харилцааг түгээхэд үндэслэсэн шинжлэх ухааны судалгааны арга юм. Экстраполяцийн аргууд орно хөдөлж буй дундаж арга, экспоненциал тэгшитгэх арга, хамгийн бага квадратын арга.

Мөн чанар хамгийн бага квадратын арга ажиглагдсан болон тооцоолсон утгуудын хоорондох квадрат хазайлтын нийлбэрийг багасгахаас бүрдэнэ. Тооцоолсон утгыг сонгосон тэгшитгэлийн дагуу олно - регрессийн тэгшитгэл. Бодит болон тооцоолсон утгуудын хоорондох зай бага байх тусам регрессийн тэгшитгэл дээр үндэслэн таамаглал илүү нарийвчлалтай болно.

Судалгаанд хамрагдаж буй үзэгдлийн мөн чанар, өөрчлөлтийг цаг хугацааны цуваагаар харуулсан онолын шинжилгээ нь муруйг сонгох үндэс суурь болдог. Цувралын түвшний өсөлтийн шинж чанарын талаархи бодол санааг заримдаа харгалзан үздэг. Тиймээс, хэрэв бүтээгдэхүүний өсөлтийг арифметик прогрессоор хүлээж байгаа бол тэгшитгэх ажлыг шулуун шугамаар гүйцэтгэдэг. Хэрэв өсөлт нь экспоненциал болж хувирвал экспоненциал функцийн дагуу жигдрүүлэх хэрэгтэй.

Хамгийн бага квадратын аргын ажлын томьёо : Y t+1 = a*X + b, энд t + 1 нь таамагласан хугацаа; Уt+1 – таамагласан үзүүлэлт; a ба b коэффициентүүд; X бол цаг хугацааны бэлгэдэл юм.

a ба b коэффициентийг дараахь томъёогоор тооцоолно.

хаана, Uf - динамикийн цувралын бодит утгууд; n - цаг хугацааны цувралын түвшний тоо;

Цагийн цувааг хамгийн бага квадратын аргаар тэгшитгэх нь судалж буй үзэгдлийн хөгжлийн зүй тогтлыг тусгах үүрэгтэй. Трендийн аналитик илэрхийлэлд цагийг бие даасан хувьсагч гэж үздэг бөгөөд цувралын түвшин нь энэхүү бие даасан хувьсагчийн функцээр ажилладаг.

Аливаа үзэгдлийн хөгжил нь эхлэлийн цэгээс хойш хэдэн жил өнгөрсөнөөс хамаарахгүй, харин түүний хөгжилд ямар хүчин зүйл нөлөөлсөн, ямар чиглэлд, ямар эрчимтэй явагдсанаас хамаардаг. Үүнээс үзэхэд аливаа үзэгдлийн хөгжил нь эдгээр хүчин зүйлсийн үйл ажиллагааны үр дүнд цаг хугацааны явцад гарч ирдэг.

Муруйн хэлбэр, цаг хугацааны аналитик хамаарлын төрлийг зөв тогтоох нь урьдчилан таамаглах шинжилгээний хамгийн хэцүү ажлуудын нэг юм. .

Параметрүүд нь хамгийн бага квадратын аргаар тодорхойлогддог чиг хандлагыг тодорхойлсон функцийн төрлийг сонгох нь ихэнх тохиолдолд эмпирик бөгөөд хэд хэдэн функцийг байгуулж, тэдгээрийг үндсэн дундаж утгаараа бие биетэйгээ харьцуулах замаар хийгддэг. - томъёогоор тооцоолсон квадрат алдаа:

хаана Uf - динамикийн цувралын бодит утгууд; Ur - хугацааны цувааны тооцоолсон (тэгшгэсэн) утгууд; n - цаг хугацааны цувралын түвшний тоо; p нь чиг хандлагыг (хөгжлийн чиг хандлага) тодорхойлсон томъёонд тодорхойлсон параметрүүдийн тоо юм.

Хамгийн бага квадратын аргын сул тал :

• судалж буй эдийн засгийн үзэгдлийг математикийн тэгшитгэл ашиглан дүрслэхийг оролдох үед таамаглал нь богино хугацаанд үнэн зөв байх бөгөөд шинэ мэдээлэл гарах үед регрессийн тэгшитгэлийг дахин тооцоолох шаардлагатай;
• стандарт компьютерийн программ ашиглан шийдвэрлэх боломжтой регрессийн тэгшитгэлийг сонгох нарийн төвөгтэй байдал.

Прогноз боловсруулахдаа хамгийн бага квадратын аргыг ашиглах жишээ

Даалгавар . Бүс нутгийн ажилгүйдлийн түвшинг тодорхойлсон тоо баримт бий, %

• Хөдөлгөөнт дундаж, экспоненциал тэгшитгэх, хамгийн бага квадрат гэсэн аргуудыг ашиглан 11, 12, 1-р саруудад бүс нутгийн ажилгүйдлийн түвшний урьдчилсан мэдээг гарга.
• Арга тус бүрийг ашиглан үр дүнгийн таамаглал дахь алдааг тооцоол.
• Хүлээн авсан үр дүнг харьцуулж, дүгнэлт гарга.

Хамгийн бага квадратын шийдэл

Шийдлийн хувьд бид шаардлагатай тооцоог хийх хүснэгтийг эмхэтгэх болно.

ε = 28.63/10 = 2.86% таамаглалын нарийвчлалөндөр.

Дүгнэлт : Тооцоололд гарсан үр дүнг харьцуулах хөдөлж буй дундаж арга , экспоненциал тэгшитгэх ба хамгийн бага квадратын аргын хувьд экспоненциал тэгшитгэх аргын тооцооны дундаж харьцангуй алдаа 20-50% -д хүрдэг гэж хэлж болно. Энэ нь энэ тохиолдолд таамаглалын нарийвчлал нь зөвхөн хангалттай гэсэн үг юм.

Эхний болон гурав дахь тохиолдолд дундаж харьцангуй алдаа 10% -иас бага байдаг тул таамаглалын нарийвчлал өндөр байна. Гэхдээ хөдөлж буй дундаж арга нь илүү найдвартай үр дүнд хүрэх боломжийг олгосон (11-р сарын урьдчилсан мэдээ - 1.52%, 12-р сарын таамаглал - 1.53%, 1-р сарын урьдчилсан мэдээ - 1.49%), учир нь энэ аргыг ашиглах үед харьцангуй дундаж алдаа хамгийн бага байдаг - 1. ,13%.

Хамгийн бага квадрат арга

Бусад холбогдох нийтлэлүүд:

Ашигласан эх сурвалжуудын жагсаалт

1. Нийгмийн эрсдэлийг оношлох, бэрхшээл, аюул занал, нийгмийн үр дагаврыг урьдчилан таамаглах асуудалд шинжлэх ухаан, арга зүйн зөвлөмж. ОХУ-ын Нийгмийн их сургууль. Москва. 2010;
2. Владимирова Л.П. Зах зээлийн нөхцөлд урьдчилан таамаглах, төлөвлөх: Proc. тэтгэмж. М .: "Дашков ба Ко" хэвлэлийн газар, 2001;
3. Новикова Н.В., Поздеева О.Г. Үндэсний эдийн засгийг таамаглах: Боловсрол, арга зүйн гарын авлага. Екатеринбург: Уралын хэвлэлийн газар. муж эдийн засаг их сургууль, 2007;
4. Слуцкин Л.Н. Бизнесийн таамаглалын чиглэлээр MBA курс. Москва: Альпин бизнесийн номууд, 2006 он.

БОЯ хөтөлбөр

Өгөгдлийг оруулна уу

Өгөгдөл ба ойролцоогоор y = a + b x

би- туршилтын цэгийн дугаар;
x i- цэг дээрх тогтмол параметрийн утга би;
y i- цэг дээрх хэмжсэн параметрийн утга би;
ω i- цэг дээрх жинг хэмжих би;
y i, тооцоолол.- хэмжсэн утга ба регрессээс тооцсон утгын зөрүү yцэг дээр би;
S x i (x i)- алдааны тооцоо x iхэмжих үед yцэг дээр би.

Өгөгдөл ба ойролцоогоор y = kx

би	x i	y i	ω i	y i, тооцоолол.	Δy би	S x i (x i)

График дээр дарна уу

MNC онлайн програмын хэрэглэгчийн гарын авлага.

Өгөгдлийн талбарт тусдаа мөр бүрт нэг туршилтын цэг дээр `x` ба `y` утгуудыг оруулна. Утга нь хоосон зайгаар (зай эсвэл таб) тусгаарлагдсан байх ёстой.

Гурав дахь утга нь `w` цэгийн жин байж болно. Хэрэв цэгийн жинг заагаагүй бол энэ нь нэгтэй тэнцүү байна. Ихэнх тохиолдолд туршилтын цэгүүдийн жин тодорхойгүй эсвэл тооцоологдоогүй; туршилтын бүх өгөгдлийг тэнцүү гэж үзнэ. Заримдаа судлагдсан утгын хүрээн дэх жин нь мэдээж тэнцүү биш бөгөөд онолын хувьд ч тооцоолж болно. Жишээлбэл, спектрофотометрийн хувьд жинг энгийн томъёогоор тооцоолж болох боловч үндсэндээ хүн бүр хөдөлмөрийн зардлыг бууруулахын тулд үүнийг үл тоомсорлодог.

Microsoft Office-ийн Excel эсвэл Open Office-ийн Calc гэх мэт оффисын багцын хүснэгтээс өгөгдлийг санах ойд буулгаж болно. Үүнийг хийхийн тулд хүснэгтээс хуулах өгөгдлийн хүрээг сонгоод санах ой руу хуулж, энэ хуудасны өгөгдлийн талбарт өгөгдлийг буулгана уу.

Хамгийн бага квадратын аргаар тооцоолохын тулд хоёр коэффициентийг тодорхойлохын тулд дор хаяж хоёр цэг шаардлагатай `b` - шулуун шугамын налуу өнцгийн тангенс ба `a` - `y дээрх шулуун шугамаар таслагдсан утга. ` тэнхлэг.

Тооцоолсон регрессийн коэффициентүүдийн алдааг тооцоолохын тулд туршилтын цэгүүдийн тоог хоёроос дээш болгох шаардлагатай.

Хамгийн бага квадратын арга (LSM).

Туршилтын цэгүүдийн тоо их байх тусам коэффициентүүдийн статистик тооцоолол (Оюутны коэффициент буурсантай холбоотой) илүү нарийвчлалтай, ерөнхий түүврийн тооцоонд ойртох болно.

Туршилтын цэг бүрт үнэ цэнийг олж авах нь ихэвчлэн их хэмжээний хөдөлмөрийн зардалтай холбоотой байдаг тул олон тооны туршилтыг ихэвчлэн хийдэг бөгөөд энэ нь шингэцтэй тооцооллыг өгдөг бөгөөд хэт их хөдөлмөрийн зардалд хүргэдэггүй. Дүрмээр бол хоёр коэффициент бүхий шугаман хамгийн бага квадратын хамаарлын туршилтын цэгүүдийн тоог 5-7 цэгийн бүсэд сонгоно.

Шугаман хамаарлын хамгийн бага квадратуудын товч онол

Бидэнд хос утгын [`y_i`, `x_i`] хэлбэрийн туршилтын өгөгдлийн багц байна гэж бодъё, энд `i` нь 1-ээс `n` хүртэлх туршилтын нэг хэмжилтийн тоо юм; `y_i` - `i` цэг дэх хэмжсэн утгын утга; `x_i` - `i` цэг дээр бидний тогтоосон параметрийн утга.

Жишээ нь Ом хуулийн үйл ажиллагаа юм. Цахилгаан хэлхээний хэсгүүдийн хоорондох хүчдэлийг (боломжийн зөрүү) өөрчилснөөр бид энэ хэсгийг дамжин өнгөрөх гүйдлийн хэмжээг хэмждэг. Физик бидэнд туршилтаар олсон хамаарлыг өгдөг.

`I=U/R`,
хаана `I` - одоогийн хүч; `R` - эсэргүүцэл; `U` - хүчдэл.

Энэ тохиолдолд `y_i` нь хэмжсэн гүйдлийн утга, `x_i` нь хүчдэлийн утга юм.

Өөр нэг жишээ болгон, уусмал дахь бодисын уусмал гэрлийн шингээлтийг авч үзье. Хими бидэнд дараах томъёог өгдөг.

`A = εl C`,
Энд `A` нь уусмалын оптик нягт; `ε` - ууссан бодисын дамжуулалт; `l` - уусмал бүхий кюветтээр гэрэл өнгөрөх үед замын урт; `C` нь ууссан бодисын концентраци юм.

Энэ тохиолдолд 'y_i' нь хэмжсэн оптик нягт 'A', 'x_i' нь бидний тогтоосон бодисын концентрац юм.

`x_i`-г тохируулах харьцангуй алдаа нь `y_i`-г хэмжих харьцангуй алдаанаас хамаагүй бага байх тохиолдлыг бид авч үзэх болно. Бид мөн 'y_i' хэмжсэн бүх утгууд нь санамсаргүй бөгөөд хэвийн тархалттай байна, өөрөөр хэлбэл. хэвийн тархалтын хуулийг дагаж мөрдөх.

`y`-ийн `x`-ээс шугаман хамаарлын хувьд онолын хамаарлыг дараах байдлаар бичиж болно.
`y = a + bx`.

Геометрийн үүднээс авч үзвэл `b` коэффициент нь шугамын `x` тэнхлэгт налуу өнцгийн шүргэгчийг, `a` коэффициент нь шугамын огтлолцлын цэг дэх `y` утгыг илэрхийлнэ. `y` тэнхлэгтэй шугам (`x = 0`-ийн хувьд).

Регрессийн шугамын параметрүүдийг олох.

Туршилтын явцад "y_i" хэмжсэн утгууд нь бодит амьдрал дээр үргэлж байдаг хэмжилтийн алдааны улмаас онолын шугам дээр яг таарч чадахгүй. Тиймээс шугаман тэгшитгэлийг тэгшитгэлийн системээр илэрхийлэх ёстой.
`y_i = a + b x_i + ε_i` (1),
Энд 'ε_i' нь 'i' туршилтын 'y' хэмжилтийн үл мэдэгдэх алдаа юм.

Хамаарал (1) гэж бас нэрлэдэг регресс, өөрөөр хэлбэл статистикийн ач холбогдол бүхий хоёр хэмжигдэхүүн бие биенээсээ хамаарах хамаарал.

Хараат байдлыг сэргээх ажил нь туршилтын цэгүүдээс [`y_i`, `x_i`] `a` ба `b` коэффициентүүдийг олох явдал юм.

"a" ба "b" коэффициентийг олохын тулд ихэвчлэн ашигладаг хамгийн бага квадрат арга(MNK). Энэ нь хамгийн их магадлалын зарчмын онцгой тохиолдол юм.

(1)-ийг `ε_i = y_i - a - b x_i` гэж дахин бичье.

Дараа нь квадрат алдааны нийлбэр болно
`Φ = нийлбэр_(i=1)^(n) ε_i^2 = нийлбэр_(i=1)^(n) (y_i - a - b x_i)^2`. (2)

Хамгийн бага квадратын аргын зарчим нь `a` ба `b` параметрүүдийн нийлбэрийг (2) багасгах явдал юм..

`a` ба `b` коэффициентүүдийн нийлбэрийн (2) хэсэгчилсэн деривативууд тэгтэй тэнцүү байх үед хамгийн багадаа хүрнэ.
`frac(хэсэгчилсэн Φ)(хэсэг a) = frac(хэсэгчилсэн нийлбэр_(i=1)^(n) (y_i - a - b x_i)^2)(хэсэг a) = 0`
`frac(хэсэгчилсэн Φ)(хэсэг b) = frac(хэсэгчилсэн нийлбэр_(i=1)^(n) (y_i - a - b x_i)^2)(хэсэг b) = 0`

Деривативуудыг өргөжүүлснээр бид хоёр үл мэдэгдэх хоёр тэгшитгэлийн системийг олж авна.
`нийлбэр_(i=1)^(n) (2a + 2bx_i - 2y_i) = нийлбэр_(i=1)^(n) (a + bx_i - y_i) = 0`
`нийлбэр_(i=1)^(n) (2bx_i^2 + 2ax_i - 2x_iy_i) = нийлбэр_(i=1)^(n) (bx_i^2 + ax_i - x_iy_i) = 0`

Бид хаалтуудыг нээж, хүссэн коэффициентээс хамааралгүй нийлбэрүүдийг нөгөө хагаст шилжүүлж, шугаман тэгшитгэлийн системийг олж авна.
`нийлбэр_(i=1)^(n) y_i = a n + b нийлбэр_(i=1)^(n) bx_i`
`нийлбэр_(i=1)^(n) x_iy_i = a нийлбэр_(i=1)^(n) x_i + b нийлбэр_(i=1)^(n) x_i^2`

Үүссэн системийг шийдэж, бид "a" ба "b" коэффициентүүдийн томъёог олно.

`a = фрак(нийлбэр_(i=1)^(n) y_i нийлбэр_(i=1)^(n) x_i^2 - нийлбэр_(i=1)^(n) x_i нийлбэр_(i=1)^(n) ) x_iy_i) (n нийлбэр_(i=1)^(n) x_i^2 — (нийлбэр_(i=1)^(n) x_i)^2)` (3.1)

`b = фрак(n нийлбэр_(i=1)^(n) x_iy_i - нийлбэр_(i=1)^(n) x_i нийлбэр_(i=1)^(n) y_i) (n нийлбэр_(i=1)^ (n) x_i^2 - (нийлбэр_(i=1)^(n) x_i)^2)` (3.2)

Эдгээр томьёо нь `n > 1` (дор хаяж 2 цэг ашиглан шугамыг зурж болно) болон тодорхойлогч `D = n нийлбэр_(i=1)^(n) x_i^2 — (нийлбэр_(i= 1) үед шийдлүүдтэй байна. )^(n) x_i)^2 != 0`, i.e. Туршилтын `x_i` цэгүүд өөр байх үед (жишээ нь шугам босоо биш үед).

Регрессийн шугамын коэффициентүүдийн алдааны тооцоо

`a` ба `b` коэффициентүүдийг тооцоолоход гарсан алдааг илүү нарийвчлалтай тооцоолохын тулд олон тооны туршилтын цэгүүдийг авах нь зүйтэй. `n = 2` үед коэффициентүүдийн алдааг тооцоолох боломжгүй, учир нь Ойролцоо шугам нь хоёр цэгээр давтагдашгүй өнгөрнө.

`V` санамсаргүй хэмжигдэхүүний алдаа тодорхойлогдоно алдааны хуримтлалын хууль
`S_V^2 = нийлбэр_(i=1)^p (фрак(хэсэг f)(хэсэг z_i))^2 S_(z_i)^2`,
Энд `p` нь `S_V` алдаанд нөлөөлөх `S_(z_i)` алдаатай `z_i` параметрийн тоо;
`f` нь `V`-ийн `z_i`-д хамаарах хамаарлын функц юм.

`a` ба `b` коэффициентүүдийн алдааны алдааны хуримтлалын хуулийг бичье.
`S_a^2 = нийлбэр_(i=1)^(n)(фрак(хэсэг а)(хэсэг y_i))^2 S_(y_i)^2 + нийлбэр_(i=1)^(n)(фрак(хэсэг а) )(хэсэгчилсэн x_i))^2 S_(x_i)^2 = S_y^2 нийлбэр_(i=1)^(n)(frac(хэсэг а)(хэсэг y_i))^2 `,
`S_b^2 = нийлбэр_(i=1)^(n)(фрак(хэсэг b)(хэсэг y_i))^2 S_(y_i)^2 + нийлбэр_(i=1)^(n)(фрак(хэсэг b) )(хэсэгчилсэн x_i))^2 S_(x_i)^2 = S_y^2 нийлбэр_(i=1)^(n)(frac(хэсэг b)(хэсэг y_i))^2 `,
учир нь `S_(x_i)^2 = 0` (бид өмнө нь `x`-ын алдаа өчүүхэн гэж тэмдэглэсэн).

`S_y^2 = S_(y_i)^2` - `y` хэмжигдэхүүн дэх алдаа (дисвэр, квадрат стандарт хазайлт), алдааг бүх `y` утгуудын хувьд жигд байна гэж үзвэл.

Үр дүнгийн илэрхийлэлд "a" ба "b"-ийг тооцоолох томъёог орлуулснаар бид олж авна.

`S_a^2 = S_y^2 фрак(нийлбэр_(i=1)^(n) (нийлбэр_(i=1)^(n) x_i^2 - x_i нийлбэр_(i=1)^(n) x_i)^2 ) (D^2) = S_y^2 фрак((n нийлбэр_(i=1)^(n) x_i^2 - (нийлбэр_(i=1)^(n) x_i)^2) нийлбэр_(i=1) ^(n) x_i^2) (D^2) = S_y^2 фрак(нийлбэр_(i=1)^(n) x_i^2) (D)` (4.1)

`S_b^2 = S_y^2 фрак(нийлбэр_(и=1)^(n) (n x_i - нийлбэр_(i=1)^(n) x_i)^2) (D^2) = S_y^2 фрак( n (n нийлбэр_(i=1)^(n) x_i^2 - (нийлбэр_(i=1)^(n) x_i)^2)) (D^2) = S_y^2 фрак(n) (D) ` (4.2)

Ихэнх бодит туршилтуудад `Sy`-ийн утгыг хэмждэггүй. Үүнийг хийхийн тулд төлөвлөгөөний нэг буюу хэд хэдэн цэг дээр хэд хэдэн зэрэгцээ хэмжилт (туршилт) хийх шаардлагатай бөгөөд энэ нь туршилтын хугацааг (болон магадгүй зардал) нэмэгдүүлдэг. Тиймээс регрессийн шугамаас `y`-ийн хазайлтыг санамсаргүй гэж үзэж болно гэж ихэвчлэн үздэг. Энэ тохиолдолд 'y' хэлбэлзлийн үнэлгээг томъёогоор тооцоолно.

`S_y^2 = S_(y, амралт)^2 = фрак(нийлбэр_(i=1)^n (y_i - a - b x_i)^2) (n-2)`.

Туршилтын ижил түүврийн өгөгдлийн хоёр коэффициентийг тооцоолсны улмаас бид эрх чөлөөний зэрэглэлийн тоог бууруулсан тул хуваагч `n-2` гарч ирнэ.

Энэ тооцоог мөн `S_(y, амралт)^2` регрессийн шугамтай харьцуулахад үлдэгдэл дисперс гэж нэрлэдэг.

Коэффициентийн ач холбогдлын үнэлгээг оюутны шалгуурын дагуу гүйцэтгэдэг

`t_a = frac(|a|) (S_a)`, `t_b = frac(|b|) (S_b)`

Хэрэв тооцоолсон `t_a`, `t_b` шалгуур үзүүлэлтүүд нь хүснэгтийн `t(P, n-2)` шалгуураас бага байвал өгөгдсөн `P` магадлалаар харгалзах коэффициент тэгээс онцын ялгаагүй гэж үзнэ.

Шугаман харилцааны тайлбарын чанарыг үнэлэхийн тулд та Фишерийн шалгуурыг ашиглан `S_(y, амралт)^2` ба `S_(bar y)`-ийг дундажтай харьцуулж болно.

`S_(бар y) = фрак(нийлбэр_(i=1)^n (y_i - багана у)^2) (n-1) = фрак(нийлбэр_(i=1)^n (y_i - (нийлбэр_(i=) 1)^n y_i) /n)^2) (n-1)` - дундажтай харьцуулахад `y`-ийн дисперсийн түүврийн тооцоо.

Хамааралтай байдлыг тодорхойлох регрессийн тэгшитгэлийн үр нөлөөг үнэлэхийн тулд Фишерийн коэффициентийг тооцоолно.
`F = S_(бар y) / S_(y, амрах)^2`,
Үүнийг хүснэгтийн Фишерийн коэффициент `F(p, n-1, n-2)`-тай харьцуулсан.

Хэрэв `F > F(P, n-1, n-2)` бол `y = f(x)` хамаарлыг регрессийн тэгшитгэл ашиглан тайлбарлах ба дундаж утгыг ашигласан тайлбарын хоорондох зөрүүг магадлалын хувьд статистикийн хувьд ач холбогдолтой гэж үзнэ. `P`. Тэдгээр. регресс нь дундаж утгын эргэн тойронд "y"-ийн тархалтаас илүү хамааралтай байдлыг илүү сайн тодорхойлдог.

График дээр дарна уу
хүснэгтэд утгыг нэмэх

Хамгийн бага квадрат арга. Хамгийн бага квадратын арга гэдэг нь үл мэдэгдэх параметрүүдийг a, b, c, хүлээн зөвшөөрөгдсөн функциональ хамаарлыг тодорхойлохыг хэлнэ.

Хамгийн бага квадратын арга нь үл мэдэгдэх параметрүүдийг тодорхойлох гэсэн үг юм a, b, c,…хүлээн зөвшөөрөгдсөн функциональ хамаарал

у = f(x,a,b,c,…),

Энэ нь алдааны дундаж квадратын (дисвэрийн) хамгийн бага хэмжээг өгөх болно

, (24)

Энд x i , y i - туршилтаас олж авсан хос тоонуудын багц.

Хэд хэдэн хувьсагчийн функцийн экстремумын нөхцөл нь түүний хэсэгчилсэн дериватив нь тэгтэй тэнцүү байх нөхцөл байдаг тул параметрүүд нь a, b, c,…тэгшитгэлийн системээр тодорхойлогддог.

; ; ; … (25)

Функцийн хэлбэрийн дараа параметрүүдийг сонгохдоо хамгийн бага квадратын аргыг ашигладаг гэдгийг санах нь зүйтэй у = f(x)тодорхойлсон.

Хэрэв онолын үүднээс авч үзвэл эмпирик томъёо нь ямар байх ёстой талаар ямар нэгэн дүгнэлт хийх боломжгүй бол харааны дүрслэл, ялангуяа ажиглагдсан өгөгдлийн график дүрслэлийг удирдан чиглүүлэх шаардлагатай.

Практикт ихэвчлэн дараахь төрлийн функцээр хязгаарлагддаг.

1) шугаман ;

2) квадрат a .

Зэрэгцүүлсний дараа бид дараах хэлбэрийн функцийг авна: g (x) = x + 1 3 + 1 .

Тохирох параметрүүдийг тооцоолох замаар бид энэ өгөгдлийг y = a x + b шугаман хамаарлаар ойролцоолж болно. Үүнийг хийхийн тулд бид хамгийн бага квадрат гэж нэрлэгддэг аргыг ашиглах хэрэгтэй болно. Туршилтын өгөгдлийг аль шугамыг хамгийн сайн уялдуулахыг шалгахын тулд та мөн зураг зурах хэрэгтэй.

OLS (хамгийн бага квадратын арга) гэж юу вэ?

Бидний хийх ёстой гол зүйл бол F (a, b) = ∑ i = 1 n (y i - (a x i + b)) 2 гэсэн хоёр хувьсагчийн функцийн утга нь шугаман хамаарлын ийм коэффициентийг олох явдал юм. хамгийн жижиг. Өөрөөр хэлбэл, a ба b-ийн тодорхой утгуудын хувьд үүссэн шулуун шугамаас танилцуулсан өгөгдлийн квадрат хазайлтын нийлбэр нь хамгийн бага утгатай байх болно. Энэ бол хамгийн бага квадратын аргын утга юм. Жишээг шийдэхийн тулд бид хоёр хувьсагчийн функцийн экстремумыг олоход л хангалттай.

Коэффициентийг тооцоолох томъёог хэрхэн гаргах вэ

Коэффициентийг тооцоолох томъёог гаргахын тулд хоёр хувьсагчтай тэгшитгэлийн системийг зохиож, шийдвэрлэх шаардлагатай. Үүнийг хийхийн тулд бид F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 илэрхийллийн хэсэгчилсэн деривативуудыг a ба b-д хамааруулан тооцож 0-тэй тэнцүүлнэ.

δ F (a , b) δ a = 0 δ F (a , b) δ b = 0 ⇔ - 2 ∑ i = 1 n (y i - (a x i + b)) x i = 0 - 2 ∑ i = 1 n ( y i - (a x i + b)) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = y ∑ i = y ∑ i = 1 1 ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i

Тэгшитгэлийн системийг шийдэхийн тулд орлуулах эсвэл Крамерын арга гэх мэт ямар ч аргыг ашиглаж болно. Үүний үр дүнд бид хамгийн бага квадратын аргыг ашиглан коэффициентийг тооцоолох томъёог авах ёстой.

n ∑ i = 1 n x i y i - ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n - ∑ i = 1 n x i 2 b = ∑ i = 1 n ∑ i - i n

Бид функц байгаа хувьсагчдын утгыг тооцоолсон
F (a , b) = ∑ i = 1 n (y i - (a x i + b)) 2 нь хамгийн бага утгыг авна. Гурав дахь догол мөрөнд бид яагаад ийм байгааг нотлох болно.

Энэ бол хамгийн бага квадратын аргыг практикт ашиглах явдал юм. a параметрийг олоход ашигладаг түүний томьёо нь ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 болон параметрийг агуулна.
n - энэ нь туршилтын өгөгдлийн хэмжээг илэрхийлнэ. Бид танд тус бүрийг тусад нь тооцохыг зөвлөж байна. Коэффицентийн утгыг b-ийн дараа шууд тооцно.

Анхны жишээ рүү буцъя.

Жишээ 1

Энд бид n нь тавтай тэнцүү байна. Коэффициентийн томъёонд орсон шаардлагатай хэмжээг тооцоолоход илүү тохиромжтой болгохын тулд бид хүснэгтийг бөглөнө.

	i = 1	би = 2	би = 3	би = 4	би = 5	∑ i = 1 5
x i	0	1	2	4	5	12
y i	2 , 1	2 , 4	2 , 6	2 , 8	3	12 , 9
x i y i	0	2 , 4	5 , 2	11 , 2	15	33 , 8
x i 2	0	1	4	16	25	46

Шийдэл

Дөрөв дэх мөрөнд хоёр дахь эгнээний утгыг i хүн бүрийн гурав дахь утгуудаар үржүүлэх замаар олж авсан өгөгдлийг агуулна. Тав дахь мөрөнд хоёр дахь квадратын өгөгдлийг агуулна. Сүүлийн баганад тусдаа мөрүүдийн утгуудын нийлбэрийг харуулав.

Бидэнд хэрэгтэй a, b коэффициентүүдийг тооцоолохдоо хамгийн бага квадратын аргыг ашиглая. Үүнийг хийхийн тулд сүүлчийн баганаас хүссэн утгыг орлуулж, нийлбэрийг тооцоолно уу.

n ∑ i = 1 n x i y i - ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n - ∑ i = 1 n x i 2 b = ∑ i = 1 n y i i - ∑ i = 1 n ∑ i = ∑ i = ∑ 1 , i - 3 - 12 12, 9 5 46 - 12 2 b = 12, 9 - a 12 5 ⇒ a ≈ 0, 165 b ≈ 2, 184

Хүссэн ойролцоох шулуун шугам нь y = 0, 165 x + 2, 184 шиг харагдах болно гэдгийг бид олж мэдсэн. Одоо бид аль шугам нь өгөгдөлд хамгийн сайн ойртохыг тодорхойлох хэрэгтэй - g (x) = x + 1 3 + 1 эсвэл 0 , 165 x + 2 , 184 . Хамгийн бага квадратын аргыг ашиглан тооцоо хийцгээе.

Алдааг тооцоолохын тулд σ 1 = ∑ i = 1 n (y i - (a x i + b i)) 2 ба σ 2 = ∑ i = 1 n (y i -) шугамуудын өгөгдлийн квадрат хазайлтын нийлбэрийг олох хэрэгтэй. g (x i)) 2 , хамгийн бага утга нь илүү тохиромжтой шугамтай тохирно.

σ 1 = ∑ i = 1 n (y i - (a x i + b i)) 2 = = ∑ i = 1 5 (y i - (0 , 165 x i + 2 , 184)) 2 ≈ 0 , 019 σ 2 = ∑ 1 n (y i - g (x i)) 2 = = ∑ i = 1 5 (y i - (x i + 1 3 + 1)) 2 ≈ 0 , 096

Хариулт:σ 1-ээс хойш< σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0, 165 x + 2, 184.

Хамгийн бага квадратын аргыг график дүрслэлд тодорхой харуулав. Улаан шугам нь шулуун шугамыг g (x) = x + 1 3 + 1, цэнхэр шугам нь y = 0, 165 x + 2, 184-ийг тэмдэглэнэ. Түүхий өгөгдлийг ягаан цэгээр тэмдэглэсэн.

Яагаад ийм төрлийн ойролцоо тооцоолол хэрэгтэй байгааг тайлбарлая.

Эдгээрийг өгөгдлийг тэгшитгэх шаардлагатай асуудлууд, мөн өгөгдлийг интерполяци хийх эсвэл экстраполяци хийх шаардлагатай асуудлуудад ашиглаж болно. Жишээлбэл, дээр дурдсан бодлогод х = 3 эсвэл x = 6 үед ажиглагдсан у хэмжигдэхүүний утгыг олж болно. Ийм жишээнүүдэд бид тусдаа өгүүллийг зориулав.

LSM аргын баталгаа

a ба b-г тооцоолоход функц хамгийн бага утгыг авахын тулд өгөгдсөн цэг дээр F (a, b) хэлбэрийн функцийн дифференциалын квадрат хэлбэрийн матриц = ∑ i = 1 n байх шаардлагатай. (y i - (a x i + b)) 2 эерэг тодорхой байна. Энэ нь хэрхэн харагдах ёстойг танд үзүүлье.

Жишээ 2

Бидэнд дараах хэлбэрийн хоёр дахь эрэмбийн дифференциал байна.

d 2 F (a ; b) = δ 2 F (a ; b) δ a 2 d 2 a + 2 δ 2 F (a ; b) δ a δ b d a d b + δ 2 F (a ; b) δ b 2 d 2б

Шийдэл

δ 2 F (a ; b) δ a 2 = δ δ F (a ; b) δ a δ a = = δ - 2 ∑ i = 1 n (y i - (a x i + b)) x i δ a = 2 ∑ i = 1 n (x i) 2 δ 2 F (a ; b) δ a δ b = δ δ F (a ; b) δ a δ b = = δ - 2 ∑ i = 1 n (y i - (a x i + b) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F (a ; b) δ b 2 = δ δ F (a ; b) δ b δ b = δ - 2 ∑ i = 1 n (y i - (a x i +) b)) δ b = 2 ∑ i = 1 n (1) = 2 n

Өөрөөр хэлбэл дараах байдлаар бичиж болно: d 2 F (a ; b) = 2 ∑ i = 1 n (x i) 2 d 2 a + 2 2 ∑ x i i = 1 n d a d b + (2 n) d 2 b .

Бид M = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n квадрат хэлбэрийн матрицыг олж авлаа.

Энэ тохиолдолд бие даасан элементүүдийн утга нь a ба b -ээс хамаарч өөрчлөгдөхгүй. Энэ матриц эерэг тодорхой мөн үү? Энэ асуултад хариулахын тулд түүний өнцгийн баганууд эерэг байгаа эсэхийг шалгацгаая.

Эхний эрэмбийн өнцгийн минорыг тооцоол: 2 ∑ i = 1 n (x i) 2 > 0 . x i цэгүүд давхцдаггүй тул тэгш бус байдал нь хатуу байна. Цаашид тооцоо хийхдээ бид үүнийг анхаарч үзэх болно.

Бид хоёр дахь эрэмбийн өнцгийн минорыг тооцоолно.

d e t (M) = 2 ∑ i = 1 n (x i) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n (x i) 2 - ∑ x i = 12

Үүний дараа бид математикийн индукц ашиглан n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 тэгш бус байдлын баталгааг үргэлжлүүлнэ.

1. Энэ тэгш бус байдал нь дурын n -д хүчинтэй эсэхийг шалгацгаая. 2-ыг аваад тооцоолъё:

2 ∑ i = 1 2 (x i) 2 - ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 - x 1 + x 2 2 = = x 1 2 - 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0

Бид зөв тэгш байдлыг олж авсан (хэрэв x 1 ба x 2 утга таарахгүй бол).

1. Энэ тэгш бус байдал нь n -ийн хувьд үнэн байх болно гэсэн таамаглал дэвшүүлье, i.e. n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 – үнэн.
2. Одоо n + 1-ийн хүчинтэй байдлыг баталъя, өөрөөр хэлбэл. (n + 1) ∑ i = 1 n + 1 (x i) 2 - ∑ i = 1 n + 1 x i 2 > 0 хэрэв n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 > 0 .

Бид тооцоолно:

(n + 1) ∑ i = 1 n + 1 (x i) 2 - ∑ i = 1 n + 1 x i 2 = = (n + 1) ∑ i = 1 n (x i) 2 + x n + 1 2 - ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n (x i) 2 + n x n + 1 2 + ∑ i = 1 n (x i) 2 + x n + 1 2 - - ∑ i = 1 n x i 2 +2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 + n x n + 1 2 - x n + 1 ∑ i = + 1 n xi = + 1 n xi n (x i) 2 = = ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 + x n + 1 2 - 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 - 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 - 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n (x i) 2 - ∑ i = 1 n x i 2 + + (x n + 1 - x 1) 2 + (x n + 1) - x 2) 2 + . . . + (x n - 1 - x n) 2 > 0

Буржгар хаалтанд оруулсан илэрхийлэл нь 0-ээс их байх болно (2-р алхам дээр бидний таамаглаж байсан зүйл дээр үндэслэн), бусад нөхцөлүүд нь бүгд тооны квадрат тул 0-ээс их байх болно. Бид тэгш бус байдлыг нотолсон.

Хариулт:олсон a ба b нь F (a, b) = ∑ i = 1 n (y i - (a x i + b)) 2 функцын хамгийн бага утгатай тохирч байх бөгөөд энэ нь тэдгээр нь хамгийн бага квадратын аргын шаардлагатай параметрүүд гэсэн үг юм. (LSM).

Хэрэв та текстэнд алдаа байгааг анзаарсан бол үүнийг тодруулаад Ctrl+Enter дарна уу

Хамгийн бага квадрат аргарегрессийн тэгшитгэлийн параметрүүдийг тооцоолоход ашигладаг.

Онцлогуудын хоорондын стохастик харилцааг судлах аргуудын нэг бол регрессийн шинжилгээ юм.
Регрессийн шинжилгээ гэдэг нь өөр (эсвэл бусад) хувьсагчийн (онцлог хүчин зүйлс) утга нь мэдэгдэж байгаа тохиолдолд санамсаргүй хэмжигдэхүүний (онцлог-үр дүн) дундаж утгыг олоход хэрэглэгддэг регрессийн тэгшитгэлийн гаралт юм. Үүнд дараах алхмууд орно.

1. холболтын хэлбэрийг сонгох (аналитик регрессийн тэгшитгэлийн төрөл);
2. тэгшитгэлийн параметрийн тооцоо;
3. аналитик регрессийн тэгшитгэлийн чанарын үнэлгээ.

Ихэнхдээ шугаман хэлбэрийг шинж чанаруудын статистик хамаарлыг тодорхойлоход ашигладаг. Шугаман харилцаанд анхаарлаа хандуулах нь түүний параметрүүдийг эдийн засгийн тодорхой тайлбарлах, хувьсагчийн өөрчлөлтөөр хязгаарлагдах, мөн ихэнх тохиолдолд шугаман бус харилцааны хэлбэрүүд хувирдаг (логарифм авах эсвэл хувьсагчийг өөрчлөх замаар) тайлбарладаг. шугаман хэлбэрт оруулан тооцоо хийх.
Шугаман хос харилцааны хувьд регрессийн тэгшитгэл нь y i =a+b·x i +u i хэлбэртэй байна. Энэ тэгшитгэлийн параметрүүдийг a ба b статистик ажиглалтын өгөгдлөөр тооцоолсон болно x ба у . Ийм үнэлгээний үр дүн нь тэгшитгэл юм: , энд , - a ба b параметрүүдийн тооцоо , - регрессийн тэгшитгэлээр олж авсан үр дүнтэй шинж чанар (хувьсагч) -ын утга (тооцсон утга).

Параметрийн тооцоололд хамгийн түгээмэл хэрэглэгддэг хамгийн бага квадратын арга (LSM).
Хамгийн бага квадратын арга нь регрессийн тэгшитгэлийн параметрүүдийн хамгийн сайн (тогтвортой, үр ашигтай, шударга бус) үнэлгээг өгдөг. Гэхдээ санамсаргүй нэр томъёо (u) болон бие даасан хувьсагч (x)-ын талаархи тодорхой таамаглалууд хангагдсан тохиолдолд л (OLS таамаглалыг үзнэ үү).

Шугаман хос тэгшитгэлийн параметрүүдийг хамгийн бага квадратын аргаар тооцоолох асуудалДараахь зүйлээс бүрдэнэ: үр дүнтэй шинж чанарын бодит утгуудын квадрат хазайлтын нийлбэр нь тооцоолсон утгуудаас y i - хамгийн бага байх параметрүүдийн ийм тооцоог олж авах.
Албан ёсоор OLS шалгуурингэж бичиж болно: .

Хамгийн бага квадратын аргуудын ангилал

1. Хамгийн бага квадрат арга.
2. Хамгийн их магадлалын арга (хэвийн сонгодог шугаман регрессийн загварын хувьд регрессийн үлдэгдлийн хэвийн байдлыг тогтооно).
3. GLSM-ийн ерөнхийлсөн хамгийн бага квадратын аргыг алдааны автокорреляци болон гетероскедастикийн тохиолдолд ашигладаг.
4. Жинлэсэн хамгийн бага квадратын арга (гетероскедастик үлдэгдэл бүхий GLSM-ийн онцгой тохиолдол).

Мөн чанарыг дүрслэн харуул Графикаар хамгийн бага квадратуудын сонгодог арга. Үүний тулд бид ажиглалтын өгөгдлийн дагуу (x i , y i , i=1;n) тэгш өнцөгт координатын системд (ийм цэгийн графикийг корреляцийн талбар гэж нэрлэдэг) цэгийн график байгуулна. Корреляцийн талбайн цэгүүдэд хамгийн ойр байгаа шулуун шугамыг олохыг хичээцгээе. Хамгийн бага квадратын аргын дагуу корреляцийн талбайн цэгүүд болон энэ шугамын хоорондох квадрат босоо зайны нийлбэр хамгийн бага байхаар шугамыг сонгоно.

Энэ асуудлын математик тэмдэглэгээ: .
y i ба x i =1...n утгууд нь бидэнд мэдэгдэж байгаа бөгөөд эдгээр нь ажиглалтын өгөгдөл юм. S функцэд тэдгээр нь тогтмол байна. Энэ функцын хувьсагч нь параметрүүдийн шаардлагатай тооцоолол юм - , . 2 хувьсагчийн функцийн хамгийн бага утгыг олохын тулд параметр тус бүртэй холбоотой энэ функцийн хэсэгчилсэн деривативыг тооцоолж, тэгтэй тэнцүүлэх шаардлагатай. .
Үүний үр дүнд бид 2 хэвийн шугаман тэгшитгэлийн системийг олж авна.
Энэ системийг шийдэж, бид шаардлагатай параметрийн тооцоог олно.

Регрессийн тэгшитгэлийн параметрүүдийн тооцооны зөв эсэхийг нийлбэрүүдийг харьцуулах замаар шалгаж болно (тооцоололыг дугуйрсанаас болж зарим зөрүү гарах боломжтой).
Параметрийн тооцоог тооцоолохын тулд 1-р хүснэгтийг үүсгэж болно.
Регрессийн коэффициент b тэмдэг нь харилцааны чиглэлийг заана (хэрэв b > 0 бол хамаарал шууд, хэрэв b бол<0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения.
Албан ёсоор a параметрийн утга нь тэгтэй тэнцүү x-ийн хувьд y-ийн дундаж утга юм. Хэрэв тэмдгийн хүчин зүйл нь тэг утгагүй ба байж чадахгүй бол a параметрийн дээрх тайлбар нь утгагүй болно.

Онцлог хоорондын харилцааны нягт байдлыг үнэлэх шугаман хос корреляцийн коэффициентийг ашиглан гүйцэтгэнэ - r x,y . Үүнийг дараах томъёогоор тооцоолж болно. . Түүнчлэн шугаман хос корреляцийн коэффициентийг b регрессийн коэффициентээр тодорхойлж болно: .
Хос корреляцийн шугаман коэффициентийн зөвшөөрөгдөх хэмжээ нь -1-ээс +1 хүртэл байна. Корреляцийн коэффициентийн тэмдэг нь харилцааны чиглэлийг заана. Хэрэв r x, y >0 бол холболт шууд байна; хэрэв r x, y<0, то связь обратная.
Хэрэв энэ коэффициент модулийн хувьд нэгдмэл байдалтай ойролцоо байвал шинж чанаруудын хоорондын хамаарлыг нэлээд ойр шугаман гэж тайлбарлаж болно. Хэрэв түүний модуль нь нэг ê r x, y ê =1-тэй тэнцүү бол шинж чанаруудын хоорондын хамаарал функциональ шугаман байна. Хэрэв x ба y шинж чанарууд нь шугаман хамааралгүй бол r x,y нь 0-тэй ойролцоо байна.
Хүснэгт 1-ийг мөн r x,y-ийг тооцоолоход ашиглаж болно.

Хүлээн авсан регрессийн тэгшитгэлийн чанарыг үнэлэхийн тулд онолын тодорхойлох коэффициентийг тооцоолно - R 2 yx:

,
Энд d 2 нь регрессийн тэгшитгэлээр тайлбарласан дисперс y;
e 2 - үлдэгдэл (регрессийн тэгшитгэлээр тайлбарлагдаагүй) дисперс y ;
s 2 y - нийт (нийт) хэлбэлзэл y .
Детерминацийн коэффициент нь регресс (мөн үүний үр дүнд х хүчин зүйл) -ээр тайлбарлагддаг үр дүнгийн y шинж чанарын өөрчлөлтийн (тархалтын) y-ийн нийт хэлбэлзлийн (тархалтын) эзлэх хувийг тодорхойлдог. Тодорхойлох коэффициент R 2 yx нь 0-ээс 1 хүртэлх утгыг авна. Үүний дагуу 1-R 2 yx утга нь загвар болон техникийн үзүүлэлтийн алдааг харгалзан үзээгүй бусад хүчин зүйлийн нөлөөллөөс үүссэн y хэлбэлзлийн эзлэх хувийг тодорхойлдог.
Хосолсон шугаман регресстэй R 2 yx =r 2 yx .

Хамгийн бага квадратын арга (OLS, англ. Ordinary Least Squares, OLS)- хүссэн хувьсагчаас зарим функцийн квадрат хазайлтын нийлбэрийг багасгахад үндэслэсэн төрөл бүрийн асуудлыг шийдвэрлэхэд ашигладаг математик арга. Үүнийг хэт тодорхойлогдсон тэгшитгэлийн системийг "шийдвэрлэх" (тэгшитгэлийн тоо нь үл мэдэгдэх тооноос давсан тохиолдолд), ердийн (хэт тодорхойлогдоогүй) шугаман бус тэгшитгэлийн системийн шийдлийг олох, цэгийн утгыг ойролцоолоход ашиглаж болно. тодорхой функцтэй. OLS нь түүврийн өгөгдлөөс регрессийн загваруудын үл мэдэгдэх параметрүүдийг тооцоолох регрессийн шинжилгээний үндсэн аргуудын нэг юм.

Нэвтэрхий толь бичиг YouTube

1 / 5

✪ Хамгийн бага квадратын арга. Сэдэв

✪ Хамгийн бага квадратууд, хичээл 1/2. Шугаман функц

✪ Эконометрик. Лекц 5. Хамгийн бага квадратын арга

✪ Митин I. V. - Физикийн үр дүнг боловсруулах. туршилт - Хамгийн бага квадратын арга (Лекц 4)

✪ Эконометрик: Хамгийн бага квадратын аргын мөн чанар №2

Хадмал орчуулга

Өгүүллэг

XIX зууны эхэн үе хүртэл. эрдэмтэд үл мэдэгдэх тоо нь тэгшитгэлийн тооноос бага байдаг тэгшитгэлийн системийг шийдвэрлэх тодорхой дүрэмгүй байсан; Тэр үеийг хүртэл тэгшитгэлийн төрөл, тооны машинуудын ухаалаг байдлаас хамааран тодорхой аргуудыг ашигладаг байсан тул ижил ажиглалтын өгөгдлөөс эхлэн өөр өөр тооцоолуур өөр өөр дүгнэлтэд хүрчээ. Гаусс (1795) аргын анхны хэрэглээ гэж тооцогддог бөгөөд Лежендре (1805) үүнийг бие даан олж, орчин үеийн нэрээр хэвлүүлсэн (fr. Арга зүй des moindres arres). Лаплас энэ аргыг магадлалын онолтой холбосон бөгөөд Америкийн математикч Адрейн (1808) түүний магадлалын хэрэглээг авч үзсэн. Энэ арга нь Энке, Бессел, Хансен болон бусад хүмүүсийн цаашдын судалгаагаар өргөн тархсан бөгөөд сайжруулсан.

Хамгийн бага квадратуудын аргын мөн чанар

Болъё x (\displaystyle x)- иж бүрдэл n (\displaystyle n)үл мэдэгдэх хувьсагч (параметрүүд), f i (x) (\displaystyle f_(i)(x)), , m > n (\displaystyle m>n)- энэ багц хувьсагчийн функцүүдийн багц. Асуудал нь ийм үнэ цэнийг сонгох явдал юм x (\displaystyle x)Ингэснээр эдгээр функцүүдийн утгууд нь зарим утгуудтай аль болох ойр байх болно y i (\displaystyle y_(i)). Үндсэндээ бид хэт тодорхойлогдсон тэгшитгэлийн системийн "шийдлийн" тухай ярьж байна f i (x) = y i (\displaystyle f_(i)(x)=y_(i)), i = 1 , … , m (\displaystyle i=1,\ldots ,m)заасан утгаараа системийн зүүн ба баруун хэсгүүдийн хамгийн их ойролцоо байдал. LSM-ийн мөн чанар нь зүүн ба баруун хэсгүүдийн квадрат хазайлтын нийлбэрийг "ойролцооны хэмжүүр" болгон сонгох явдал юм. | f i (x) − y i | (\displaystyle |f_(i)(x)-y_(i)|). Тиймээс LSM-ийн мөн чанарыг дараах байдлаар илэрхийлж болно.

∑ i e i 2 = ∑ i (y i − f i (x)) 2 → min x (\displaystyle \sum _(i)e_(i)^(2)=\sum _(i)(y_(i)-f_() i)(x))^(2)\баруун сум \мин _(x)).

Хэрэв тэгшитгэлийн систем шийдэлтэй бол квадратуудын нийлбэрийн хамгийн бага нь тэгтэй тэнцүү байх бөгөөд тэгшитгэлийн системийн яг шийдлийг аналитик аргаар эсвэл жишээлбэл, янз бүрийн тоон оновчлолын аргаар олж болно. Хэрэв систем хэт тодорхойлогдсон, өөрөөр хэлбэл үл хамаарах тэгшитгэлийн тоо үл мэдэгдэх хувьсагчийн тооноос их байвал системд яг тодорхой шийдэл байхгүй бөгөөд хамгийн бага квадратын арга нь "оновчтой" векторыг олох боломжийг олгодог. x (\displaystyle x)векторуудын хамгийн их ойр байх утгаараа y (\displaystyle y)болон f (x) (\displaystyle f(x))эсвэл хазайлтын векторын хамгийн их ойр байх e (\displaystyle e)тэг хүртэл (ойролцоо гэдэг нь Евклидийн зай гэсэн утгаар ойлгогдоно).

Жишээ - шугаман тэгшитгэлийн систем

Ялангуяа шугаман тэгшитгэлийн системийг "шийдэхэд" хамгийн бага квадратын аргыг ашиглаж болно

A x = b (\displaystyle Ax=b),

хаана A (\displaystyle A)тэгш өнцөгт хэмжээтэй матриц m × n , m > n (\displaystyle m\times n,m>n)(өөрөөр хэлбэл А матрицын мөрийн тоо нь шаардлагатай хувьсагчийн тооноос их байна).

Ийм тэгшитгэлийн системд ерөнхийдөө шийдэл байдаггүй. Тиймээс ийм векторыг сонгох утгаар л энэ системийг "шийдвэрлэх" боломжтой x (\displaystyle x)векторуудын хоорондох "зай" -ыг багасгах A x (\displaystyle Ax)болон b (\displaystyle b). Үүнийг хийхийн тулд та системийн тэгшитгэлийн зүүн ба баруун хэсгүүдийн квадрат ялгааны нийлбэрийг багасгах шалгуурыг ашиглаж болно, өөрөөр хэлбэл (A x − b) T (A x − b) → min x (\displaystyle (Ax-b)^(T)(Ax-b)\баруун сум \мин _(x)). Энэхүү багасгах бодлогын шийдэл нь дараах тэгшитгэлийн системийн шийдэлд хүргэдэг болохыг харуулахад хялбар байдаг

A T A x = A T b ⇒ x = (A T A) − 1 A T b (\displaystyle A^(T)Ax=A^(T)b\Баруун сум x=(A^(T)A)^(-1)A^ (T)b).

Регрессийн шинжилгээнд OLS (өгөгдлийн ойролцоо)

Байг n (\displaystyle n)зарим хувьсагчийн утгууд y (\displaystyle y)(энэ нь ажиглалт, туршилт гэх мэт үр дүн байж болно) болон холбогдох хувьсагчид x (\displaystyle x). Сорилт нь хоорондын харилцааг бий болгох явдал юм y (\displaystyle y)болон x (\displaystyle x)зарим үл мэдэгдэх параметр хүртэл мэдэгдэж буй зарим функцээр ойролцоогоор b (\displaystyle b), өөрөөр хэлбэл параметрүүдийн хамгийн сайн утгыг олох b (\displaystyle b), утгуудыг дээд зэргээр ойртуулж байна f (x , b) (\displaystyle f(x,b))бодит үнэ цэнэ рүү y (\displaystyle y). Үнэн хэрэгтээ энэ нь хэт тодорхойлогдсон тэгшитгэлийн системийг "шийдвэрлэх" тохиолдол болж буурдаг b (\displaystyle b):

F (x t , b) = y t , t = 1 , … , n (\displaystyle f(x_(t),b)=y_(t),t=1,\ldots ,n).

Регрессийн шинжилгээ, ялангуяа эконометрикийн хувьд хувьсагчдын хоорондын хамаарлын магадлалын загварыг ашигладаг.

Y t = f (x t , b) + ε t (\displaystyle y_(t)=f(x_(t),b)+\varepsilon _(t)),

хаана ε t (\displaystyle \varepsilon _(t))- гэж нэрлэдэг санамсаргүй алдаазагварууд.

Үүний дагуу ажиглагдсан утгуудын хазайлт y (\displaystyle y)загвараас f (x , b) (\displaystyle f(x,b))загварт аль хэдийн таамагласан. LSM-ийн мөн чанар (энгийн, сонгодог) нь ийм параметрүүдийг олох явдал юм b (\displaystyle b), үүнд квадрат хазайлтын нийлбэр (алдаа, регрессийн загваруудын хувьд тэдгээрийг ихэвчлэн регрессийн үлдэгдэл гэж нэрлэдэг) e t (\displaystyle e_(t))хамгийн бага байх болно:

b ^ O L S = arg ⁡ мин b R S S (b) (\displaystyle (\малгай (б))_(OLS)=\arg \min _(b)RSS(b)),

хаана R S S (\displaystyle RSS)- Англи хэл. Квадратуудын үлдэгдэл нийлбэрийг дараах байдлаар тодорхойлно.

R S S (b) = e T e = ∑ t = 1 n e t 2 = ∑ t = 1 n (y t − f (x t , b)) 2 (\displaystyle RSS(b)=e^(T)e=\нийлбэр _ (t=1)^(n)e_(t)^(2)=\нийлбэр _(t=1)^(n)(y_(t)-f(x_(t),b))^(2) ).

Ерөнхий тохиолдолд энэ асуудлыг тоон аргаар оновчтой болгох (багаруулах) аргаар шийдэж болно. Энэ тохиолдолд нэг нь ярьдаг шугаман бус хамгийн бага квадратууд(NLS эсвэл NLLS - eng. Non Linear Least Squares). Ихэнх тохиолдолд аналитик шийдлийг олж авч болно. Багасгах асуудлыг шийдэхийн тулд функцийн суурин цэгүүдийг олох шаардлагатай R S S (b) (\displaystyle RSS(b)), үл мэдэгдэх параметрүүдээр ялгах b (\displaystyle b), деривативуудыг тэгтэй тэнцүүлж, үүссэн тэгшитгэлийн системийг шийдэх:

∑ t = 1 n (y t − f (x t , b)) ∂ f (x t , b) ∂ b = 0 (\displaystyle \sum _(t=1)^(n)(y_(t)-f(x_) (t),b))(\frac (\хэсэг f(x_(t),b))(\хэсэг b))=0).

Шугаман регрессийн тохиолдолд LSM

Регрессийн хамаарлыг шугаман гэж үзье.

y t = ∑ j = 1 k b j x t j + ε = x t T b + ε t (\displaystyle y_(t)=\sum _(j=1)^(k)b_(j)x_(tj)+\varepsilon =x_( t)^(T)b+\varepsilon _(t)).

Болъё yтайлбарлаж буй хувьсагчийн ажиглалтын баганын вектор ба X (\displaystyle X)- энэ бол (n × k) (\displaystyle ((n\times k)))- хүчин зүйлсийн ажиглалтын матриц (матрицын мөрүүд - өгөгдсөн ажиглалтын хүчин зүйлийн утгын векторууд, баганаар - бүх ажиглалт дахь өгөгдсөн хүчин зүйлийн утгын вектор). Шугаман загварын матрицын дүрслэл нь дараах хэлбэртэй байна.

y = Xb + ε (\displaystyle y=Xb+\varepsilon).

Дараа нь тайлбарласан хувьсагчийн үнэлгээний вектор ба регрессийн үлдэгдэл вектор нь тэнцүү байх болно.

y ^ = X b , e = y − y ^ = y − X b (\displaystyle (\hat (y))=Xb,\quad e=y-(\hat (y))=y-Xb).

үүний дагуу регрессийн үлдэгдлийн квадратуудын нийлбэр тэнцүү байна

R S S = e T e = (y - X b) T (y - X b) (\displaystyle RSS=e^(T)e=(y-Xb)^(T)(y-Xb)).

Энэ функцийг параметрийн векторын хувьд ялгах b (\displaystyle b)ба деривативуудыг тэгтэй тэнцүүлснээр бид тэгшитгэлийн системийг олж авна (матриц хэлбэрээр):

(X T X) b = X T y (\displaystyle (X^(T)X)b=X^(T)y).

Шифрлэгдсэн матриц хэлбэрээр энэ тэгшитгэлийн систем дараах байдалтай байна.

(∑ x t 1 2 ∑ x t 1 x t 2 ∑ x t 1 x t 3 … ∑ x t 1 x t k ∑ x t 2 x t 1 ∑ x t 2 2 ∑ x t 2 x t 3 … ∑ x t 2 x t 3 … ∑ x t 2 x t 3 … ∑ x t 3 x t k ⋮ ⋮ ⋮ ⋱ ⋮ ∑ x t k x t 1 ∑ x t k x t 2 ∑ x t k x t 3 … ∑ x t k 2) (b 1 b 2 b 3 ⋮ b k) = (∑ x t 1 y x t ∑ 3 y t ⋮ ∑ x t k y t) , (\displaystyle (\begin(pmatrix)\sum x_(t1)^(2)&\sum x_(t1)x_(t2)&\sum x_(t1)x_(t3)&\ldots &\sum x_(t1)x_( tk)\\\ нийлбэр x_(t2)x_(t1)&\нийлбэр x_(t2)^(2)&\нийлбэр x_(t2)x_(t3)&\ldots &\ нийлбэр x_(t2)x_(tk) \\\нийлбэр x_(t3)x_(t1)&\sum x_(t3)x_(t2)&\sum x_(t3)^(2)&\ldots &\sum x_ (t3)x_(tk)\\ \vdots &\vdots &\vdots &\ddots &\vdots \\\sum x_(tk)x_(t1)&\sum x_(tk)x_(t2)&\sum x_ (tk)x_(t3)&\ ldots &\sum x_(tk)^(2)\\\end(pmatrix))(\begin(pmatrix)b_(1)\\b_(2)\\b_(3 )\\\vdots \\b_( k)\\\төгсгөл(pmatrix))=(\эхлэх(pmatrix)\sum x_(t1)y_(t)\\\sum x_(t2)y_(t)\\ \sum x_(t3)y_(t) )\\\vdots \\\ нийлбэр x_(tk)y_(t)\\\end(pmatrix)))бүх нийлбэрийг бүх зөвшөөрөгдөх утгуудаас авсан t (\displaystyle t).

Хэрэв загварт тогтмолыг оруулсан бол (ердийнх шиг), дараа нь x t 1 = 1 (\displaystyle x_(t1)=1)бүгдэд нь t (\displaystyle t), тиймээс тэгшитгэлийн системийн матрицын зүүн дээд буланд ажиглалтын тоо байна. n (\displaystyle n), мөн эхний мөр ба эхний баганын үлдсэн элементүүдэд - зөвхөн хувьсагчийн утгуудын нийлбэр: ∑ x t j (\displaystyle \sum x_(tj))ба системийн баруун талын эхний элемент - ∑ y t (\displaystyle \sum y_(t)).

Энэхүү тэгшитгэлийн системийн шийдэл нь шугаман загварын хамгийн бага квадратын тооцооны ерөнхий томъёог өгдөг.

b ^ O L S = (X T X) − 1 X T y = (1 n X T X) − 1 1 n X T y = V x − 1 C x y (\displaystyle (\малгай (b))_(OLS)=(X^(T) )X)^(-1)X^(T)y=\left((\frac (1)(n))X^(T)X\баруун)^(-1)(\frac (1)(n) ))X^(T)y=V_(x)^(-1)C_(xy)).

Аналитик зорилгоор энэ томьёоны сүүлчийн дүрслэл нь ашигтай болж хувирдаг (тэгшитгэлийн системд n-д хуваагдах үед нийлбэрийн оронд арифметик хэрэгсэл гарч ирдэг). Хэрэв регрессийн загварт өгөгдөл төвтэй, тэгвэл энэ дүрслэлд эхний матриц нь хүчин зүйлсийн түүврийн ковариацын матрицын утгатай, хоёр дахь нь хамааралтай хувьсагчтай хүчин зүйлсийн ковариацын вектор юм. Хэрэв, үүнээс гадна, өгөгдөл нь мөн хэвийн болгосон SKO-д (энэ нь эцсийн эцэст стандартчилагдсан), дараа нь эхний матриц нь хүчин зүйлийн түүврийн корреляцийн матриц, хоёр дахь вектор нь хамааралтай хувьсагчтай хүчин зүйлсийн түүвэр корреляцийн вектор гэсэн утгатай байна.

Загваруудын LLS тооцооны чухал шинж чанар тогтмолтой- баригдсан регрессийн шугам нь түүврийн өгөгдлийн хүндийн төвөөр дамждаг, өөрөөр хэлбэл тэгш байдал хангагдсан болно.

y ¯ = b 1 ^ + ∑ j = 2 k b ^ j x ¯ j (\displaystyle (\bar (y))=(\малгай (b_(1)))+\нийлбэр _(j=2)^(k) (\малгай (б))_(ж)(\бар (x))_(j)).

Ялангуяа онцгой тохиолдолд, цорын ганц регрессор тогтмол байх үед бид нэг параметрийн OLS үнэлгээ (тогтмол өөрөө) тайлбарлаж буй хувьсагчийн дундаж утгатай тэнцүү болохыг олж мэднэ. Өөрөөр хэлбэл, олон тооны хуулиас сайн шинж чанараараа алдартай арифметик дундаж нь мөн хамгийн бага квадратын тооцоолол юм - энэ нь түүнээс хазайсан квадратын хамгийн бага нийлбэрийн шалгуурыг хангадаг.

Хамгийн энгийн онцгой тохиолдлууд

Хос шугаман регрессийн хувьд y t = a + b x t + ε t (\displaystyle y_(t)=a+bx_(t)+\varepsilon _(t)), нэг хувьсагчийн нөгөө хувьсагчийн шугаман хамаарлыг тооцоолох үед тооцооллын томъёог хялбаршуулдаг (та матриц алгебргүйгээр хийж болно). Тэгшитгэлийн систем нь дараах хэлбэртэй байна.

(1 x ¯ x ¯ x 2 ¯) (a b) = (y ¯ x y ¯) (\displaystyle (\begin(pmatrix)1&(\bar (x))\\(\bar (x))&(\bar) (x^(2)))\\\end(pmatrix))(\begin(pmatrix)a\\b\\\end(pmatrix))=(\begin(pmatrix)(\bar (y))\\ (\overline(xy))\\\end(pmatrix))).

Эндээс коэффициентүүдийн тооцоог олоход хялбар байдаг.

( b ^ = Cov ⁡ (x , y) Var ⁡ (x) = x y ¯ − x ¯ y ¯ x 2 ¯ − x ¯ 2 , a ^ = y ¯ − b x ¯ . (\displaystyle (\эхлэх(тохиолдол)) (\hat (b))=(\frac (\mathop (\textrm (Cov)) (x,y))(\mathop (\textrm (Var)) (x)))=(\frac ((\overline) (xy))-(\bar (x))(\bar (y))))((\overline (x^(2)))-(\overline (x))^(2))),\\( \hat (a))=(\bar (y))-b(\bar (x)).\төгсгөл(тохиолдлууд)))

Ерөнхийдөө тогтмол хэмжигдэхүүнтэй загваруудыг илүүд үздэг хэдий ч зарим тохиолдолд онолын үүднээс авч үзвэл тогтмол байдаг. a (\displaystyle a)тэгтэй тэнцүү байх ёстой. Жишээлбэл, физикийн хувьд хүчдэл ба гүйдлийн хоорондын хамаарал нь хэлбэртэй байдаг U = I ⋅ R (\displaystyle U=I\cdot R); Хүчдэл ба гүйдлийг хэмжихдээ эсэргүүцлийг тооцоолох шаардлагатай. Энэ тохиолдолд бид загварын тухай ярьж байна y = b x (\displaystyle y=bx). Энэ тохиолдолд тэгшитгэлийн системийн оронд бид нэг тэгшитгэлтэй болно

(∑ x t 2) b = ∑ x t y t (\displaystyle \left(\sum x_(t)^(2)\right)b=\sum x_(t)y_(t)).

Тиймээс нэг коэффициентийг тооцоолох томъёо нь хэлбэртэй байна

B ^ = ∑ t = 1 n x t y t ∑ t = 1 n x t 2 = x y ¯ x 2 ¯ (\displaystyle (\малгай (b))=(\frac (\sum _(t=1)^(n)x_(t) )y_(t))(\sum _(t=1)^(n)x_(t)^(2)))=(\frac (\overline (xy))(\overline (x^(2)) ))).

Олон гишүүнт загварын тохиолдол

Хэрэв өгөгдөл нь нэг хувьсагчийн олон гишүүнт регрессийн функцээр тоноглогдсон бол f (x) = b 0 + ∑ i = 1 k b i x i (\displaystyle f(x)=b_(0)+\нийлбэр \хязгаар _(i=1)^(k)b_(i)x^(i)), дараа нь, мэдрэх зэрэг x i (\displaystyle x^(i))тус бүрийн хувьд бие даасан хүчин зүйлүүд би (\displaystyle i)шугаман загварын параметрүүдийг тооцох ерөнхий томьёоны үндсэн дээр загварын параметрүүдийг тооцоолох боломжтой. Үүнийг хийхийн тулд ерөнхий томъёонд ийм тайлбарыг анхаарч үзэх нь хангалттай юм x t i x t j = x t i x t j = x t i + j (\displaystyle x_(ti)x_(tj)=x_(t)^(i)x_(t)^(j)=x_(t)^(i+j))болон x t j y t = x t j y t (\displaystyle x_(tj)y_(t)=x_(t)^(j)y_(t)). Тиймээс энэ тохиолдолд матрицын тэгшитгэл нь дараах хэлбэртэй байна.

(n ∑ n x t ... ∑ n x t k ∑ n x t ∑ n x t 2 ... ∑ n x t k + 1 ⋮ ⋱ ⋮ ∑ n x t k ∑ n x t k + 1 ... ∑ y [∑t k [∑t = b [∑t ] [∑t 1] ∑ n x t y t ⋮ n x t k y t ] . (\ displaystyle (\begin(pmatrix)n&\sum \limits _(n)x_(t)&\ldots &\sum \limits _(n)x_(t)^(k)\\\sum \limits _( n)x_(t)&\sum \limits _(n)x_(t)^(2)&\ldots &\sum \limits _(n)x_(t)^(k+1)\\\vdots & \vdots &\ddots &\vdots \\\sum \limits _(n)x_(t)^(k)&\sum \limits _(n)x_(t)^(k+1)&\ldots &\ нийлбэр \хязгаарууд _(n)x_(t)^(2k)\төгсгөл(pmatrix))(\эхлэх(bmatrix)b_(0)\\b_(1)\\\vdots \\b_(k)\end( bматриц))=(\эхлэх(бматриц)\нийлбэр \хязгаарууд _(n)y_(t)\\\ нийлбэр \хязгаарууд _(n)x_(t)y_(t)\\\vdots \\\ нийлбэр \хязгаар _(n)x_(t)^(k)y_(t)\end(bматриц)).)

OLS тооцооллын статистик шинж чанарууд

Юуны өмнө бид шугаман загваруудын хувьд хамгийн бага квадратын тооцоолол нь дээрх томьёоны дагуу шугаман тооцоолол гэдгийг бид тэмдэглэж байна. Хамгийн бага квадратын тооцооллыг шударга байлгахын тулд регрессийн шинжилгээний хамгийн чухал нөхцлийг биелүүлэх нь зайлшгүй бөгөөд хангалттай юм: хүчин зүйлээс хамааралтай санамсаргүй алдааны математик хүлээлт тэгтэй тэнцүү байх ёстой. Энэ нөхцөл хангагдсан, тухайлбал, хэрэв

1. санамсаргүй алдааны математикийн хүлээлт тэг, ба
2. хүчин зүйлс болон санамсаргүй алдаа нь бие даасан санамсаргүй  утга юм.

Хоёрдахь нөхцөл - экзоген хүчин зүйлийн нөхцөл нь суурь юм. Хэрэв энэ өмч нь сэтгэл хангалуун бус байвал бараг бүх тооцоо нь туйлын хангалтгүй байх болно гэж бид таамаглаж болно: тэдгээр нь бүр тогтвортой биш байх болно (өөрөөр хэлбэл маш их хэмжээний мэдээлэл ч гэсэн энэ тохиолдолд чанарын тооцоо хийх боломжийг олгодоггүй). Сонгодог тохиолдолд санамсаргүй алдаанаас ялгаатай нь хүчин зүйлийн детерминизмын талаар илүү хүчтэй таамаглал дэвшүүлсэн бөгөөд энэ нь автоматаар экзоген нөхцөл хангагдсан гэсэн үг юм. Ерөнхий тохиолдолд тооцооллыг нийцүүлэхийн тулд матрицын нийлмэл байдлын хамт экзогенийн нөхцлийг хангахад хангалттай. V x (\displaystyle V_(x))түүврийн хэмжээ хязгааргүй хүртэл өсөхөд зарим доройтдоггүй матриц руу.

Тохиромжтой, шударга байдлаас гадна (ердийн) хамгийн бага квадратуудын тооцоо үр дүнтэй байхын тулд (шугаман бус үнэлгээний ангилалд хамгийн сайн нь) санамсаргүй алдааны нэмэлт шинж чанарыг хангах шаардлагатай.

Эдгээр таамаглалыг санамсаргүй алдааны векторын ковариацын матрицад зориулж томъёолж болно. V (ε) = σ 2 I (\displaystyle V(\varepsilon)=\сигма ^(2)I).

Эдгээр нөхцлийг хангасан шугаман загварыг гэнэ сонгодог. Сонгодог шугаман регрессийн OLS тооцоолол нь бүх шугаман шударга бус тооцооллын ангилалд хамааралгүй, тууштай, хамгийн үр дүнтэй тооцоолол юм (Англи хэл дээрх товчлолыг заримдаа ашигладаг. цэнхэр (Шилдэг шугаман бус тооцоологч) хамгийн сайн шугаман бус үнэлгээ; дотоодын уран зохиолд Гаусс - Марковын теоремыг ихэвчлэн иш татдаг). Үзүүлэхэд хялбар тул коэффициентийн тооцооллын векторын ковариацын матриц нь дараахтай тэнцүү байна.

V (b ^ O L S) = σ 2 (X T X) − 1 (\displaystyle V((\малгай (б))_(OLS))=\sigma ^(2)(X^(T)X)^(-1) )).

Үр ашиг гэдэг нь энэхүү ковариацын матриц нь "хамгийн бага" гэсэн үг юм (коэффициентуудын аль ч шугаман хослол, ялангуяа коэффициентүүд нь хамгийн бага хэлбэлзэлтэй байдаг), өөрөөр хэлбэл шугаман шударга бус тооцооллын ангилалд OLS тооцоолол хамгийн сайн байдаг. Энэхүү матрицын диагональ элементүүд - коэффициентүүдийн үнэлгээний хэлбэлзэл нь олж авсан тооцооллын чанарын чухал үзүүлэлтүүд юм. Гэхдээ санамсаргүй алдааны дисперс тодорхойгүй тул ковариацын матрицыг тооцоолох боломжгүй. Санамсаргүй алдааны дисперсийг шударга бус, тууштай (сонгодог шугаман загварын хувьд) үнэлэмж нь дараах утгатай болохыг баталж болно.

S 2 = R S S / (n − k) (\displaystyle s^(2)=RSS/(n-k)).

Энэ утгыг ковариацын матрицын томъёонд орлуулснаар бид ковариацын матрицын тооцооллыг олж авна. Үүний үр дүнд хийсэн тооцоолол нь бас нэг талыг барьсан, тууштай байна. Мөн алдааны дисперсийн тооцоо (тиймээс коэффициентүүдийн хэлбэлзэл) болон загварын параметрүүдийн тооцоолол нь бие даасан санамсаргүй хэмжигдэхүүн байх нь чухал бөгөөд энэ нь загварын коэффициентүүдийн талаархи таамаглалыг шалгах тестийн статистикийг олж авах боломжийг олгодог.

Хэрэв сонгодог таамаглал хангагдаагүй бол хамгийн бага квадратын параметрийн тооцоо нь хамгийн үр дүнтэй биш гэдгийг тэмдэглэх нь зүйтэй. W (\displaystyle W)нь тэгш хэмтэй эерэг тодорхой жинтэй матриц юм. Жингийн матриц нь таних матрицтай пропорциональ байх үед энгийн хамгийн бага квадратууд нь энэ аргын онцгой тохиолдол юм. Мэдэгдэж байгаагаар тэгш хэмтэй матрицуудын (эсвэл операторуудын) хувьд задрал байдаг W = P T P (\displaystyle W=P^(T)P). Тиймээс энэ функцийг дараах байдлаар илэрхийлж болно e T P T P e = (P e) T P e = e ∗ T e ∗ (\displaystyle e^(T)P^(T)Pe=(Pe)^(T)Pe=e_(*)^(T)e_( *)), өөрөөр хэлбэл, энэ функцийг зарим хувиргасан "үлдэгдэл" -ийн квадратуудын нийлбэрээр илэрхийлж болно. Тиймээс бид хамгийн бага квадратын аргуудын ангиллыг ялгаж салгаж болно - LS арга (Бага квадратууд).

Ерөнхий шугаман регрессийн загварт (санамсаргүй алдааны ковариацын матрицад ямар ч хязгаарлалт тавьдаггүй) хамгийн үр дүнтэй (шугаман бус үнэлгээний ангилалд) гэж нэрлэгддэг тооцоолол байдаг нь (Айткенийн теорем) батлагдсан. ерөнхий OLS (OMNK, GLS - Ерөнхий жижиг квадратууд)- Санамсаргүй алдааны урвуу ковариацын матрицтай тэнцүү жинтэй матрицтай LS арга: W = V ε − 1 (\displaystyle W=V_(\varepsilon )^(-1)).

Шугаман загварын параметрүүдийн GLS-үнэлгээний томъёо нь хэлбэртэй байгааг харуулж болно

B ^ G L S = (X T V − 1 X) − 1 X T V − 1 y (\displaystyle (\малгай (b))_(GLS)=(X^(T)V^(-1)X)^(-1) X^(T)V^(-1)y).

Эдгээр тооцооллын ковариацын матриц нь тэнцүү байх болно

V (b ^ G L S) = (X T V − 1 X) − 1 (\displaystyle V((\малгай (б))_(GLS))=(X^(T)V^(-1)X)^(- нэг)).

Үнэн хэрэгтээ OLS-ийн мөн чанар нь анхны өгөгдлийн тодорхой (шугаман) хувиргалт (P) болон хувирсан өгөгдөлд ердийн хамгийн бага квадратуудыг ашиглахад оршдог. Энэхүү хувиргалтын зорилго нь хувиргасан өгөгдлийн хувьд санамсаргүй алдаа нь сонгодог таамаглалыг аль хэдийн хангасан байх явдал юм.

Жинлэсэн хамгийн бага квадратууд

Диагональ жингийн матриц (мөн санамсаргүй алдааны ковариацын матриц) тохиолдолд бид хамгийн бага жинтэй квадратууд гэж нэрлэгддэг (WLS - Weighted Least Squares). Энэ тохиолдолд загварын үлдэгдлийн квадратуудын жигнэсэн нийлбэрийг багасгасан, өөрөөр хэлбэл ажиглалт бүр нь энэхүү ажиглалтын санамсаргүй алдааны хэлбэлзэлтэй урвуу хамааралтай "жин"-ийг хүлээн авдаг. e T W e = ∑ t = 1 n e t 2 σ t 2 (\displaystyle e^(T)We=\sum _(t=1)^(n)(\frac (e_(t)^(2))(\) сигма _(t)^(2)))). Үнэн хэрэгтээ, ажиглалтыг жинлэх замаар өгөгдлийг хувиргадаг (санамсаргүй алдааны стандарт хазайлттай пропорциональ хэмжээгээр хуваах), жинлэсэн өгөгдөлд ердийн хамгийн бага квадратуудыг ашигладаг.

ISBN 978-5-7749-0473-0.

Эконометрик. Сурах бичиг / Ed. Елисеева I. I. - 2-р хэвлэл. - М.: Санхүү, статистик, 2006. - 576 х. - ISBN 5-279-02786-3.

Александрова Н.В.Математикийн нэр томъёо, ойлголт, тэмдэглэгээний түүх: толь бичиг, лавлах ном. - 3-р хэвлэл - М.: LKI, 2008. - 248 х. - ISBN 978-5-382-00839-4.И.В.Митин, Русаков В.С. Туршилтын өгөгдөлд дүн шинжилгээ хийх, боловсруулах - 5-р хэвлэл - 24х.