La loi de distribution d'une variable aléatoire consiste à trouver l'espérance mathématique. Variables aléatoires discrètes. loi de distribution d'une variable aléatoire discrète
Chapitre 1. Discret valeur aléatoire
§ 1. Le concept de variable aléatoire.
La loi de distribution d'une variable aléatoire discrète.
Définition : Aléatoire est une grandeur qui, à la suite du test, ne prend qu'une seule valeur parmi un ensemble possible de ses valeurs, inconnues à l'avance et dépendant de causes aléatoires.
Il existe deux types de variables aléatoires : discrètes et continues.
Définition : La variable aléatoire X est appelée discret (discontinu) si l'ensemble de ses valeurs est fini ou infini, mais dénombrable.
En d'autres termes, les valeurs possibles d'une variable aléatoire discrète peuvent être renumérotées.
Vous pouvez décrire une variable aléatoire à l'aide de sa loi de distribution.
Définition : La loi de distribution d'une variable aléatoire discrète appelé la correspondance entre les valeurs possibles d'une variable aléatoire et leurs probabilités.
La loi de distribution d'une variable aléatoire discrète X peut être donnée sous la forme d'un tableau, dans la première ligne duquel toutes les valeurs possibles de la variable aléatoire sont indiquées par ordre croissant, et dans la deuxième ligne les probabilités correspondantes de celles-ci valeurs, c'est-à-dire
où ð1+ ð2+…+ ðn=1
Un tel tableau est appelé une série de distribution d'une variable aléatoire discrète.
Si l'ensemble des valeurs possibles d'une variable aléatoire est infini, alors la série р1+ р2+…+ рn+… converge et sa somme est égale à 1.
La loi de distribution d'une variable aléatoire discrète X peut être représentée graphiquement, pour laquelle dans système rectangulaire coordonnées, une polyligne est construite reliant successivement les points de coordonnées (xi;pi), i=1,2,…n. La ligne résultante s'appelle polygone de distribution (Fig. 1).
La chimie organique "href="/text/category/organicheskaya_hiimya/" rel="bookmark"> de la chimie organique est respectivement égale à 0,7 et 0,8. Établissez la loi de distribution de la variable aléatoire X - le nombre d'examens que l'étudiant passera.
La solution. A la suite de l'examen, la variable aléatoire X considérée peut prendre l'une des valeurs suivantes : x1=0, x2=1, x3=2.
Trouvons la probabilité de ces valeurs. Dénotons les événements :
https://pandia.ru/text/78/455/images/image004_81.jpg" width="259" height="66 src=">
 |
Ainsi, la loi de distribution de la variable aléatoire X est donnée par le tableau :
Contrôle : 0,6+0,38+0,56=1.
§ 2. Fonction de répartition
Une description complète d'une variable aléatoire est également donnée par la fonction de distribution.
Définition: La fonction de distribution d'une variable aléatoire discrète X on appelle la fonction F(x) qui détermine pour chaque valeur x la probabilité que la variable aléatoire X prenne une valeur inférieure à x :
F(x)=P(X<х)
Géométriquement, la fonction de distribution est interprétée comme la probabilité qu'une variable aléatoire X prenne la valeur représentée sur la droite numérique par un point à gauche du point x.
1)0≤F(x)≤1 ;
2) F(x) est une fonction non décroissante sur (-∞;+∞);
3) F(x) - continue à partir de la gauche aux points x= xi (i=1,2,…n) et continue à tous les autres points ;
4) F(-∞)=P (X<-∞)=0 как вероятность невозможного события Х<-∞,
F(+∞)=P(X<+∞)=1 как вероятность достоверного события Х<-∞.
Si la loi de distribution d'une variable aléatoire discrète X est donnée sous forme de tableau :
alors la fonction de distribution F(x) est déterminée par la formule :
https://pandia.ru/text/78/455/images/image007_76.gif" height="110">
0 pour x≤ x1,
p1 à x1< х≤ x2,
F(x)= p1 + p2 en x2< х≤ х3
1 pour x> xn.
Son graphique est représenté sur la Fig. 2 :
§ 3. Caractéristiques numériques d'une variable aléatoire discrète.
Parmi les caractéristiques numériques importantes figure valeur attendue.
Définition: Espérance mathématique M(X) La variable aléatoire discrète X est la somme des produits de toutes ses valeurs et de leurs probabilités correspondantes :
M(X) = ∑ xiрi= x1р1 + x2р2+…+ xnрn
L'espérance mathématique sert de caractéristique de la valeur moyenne d'une variable aléatoire.
Propriétés de l'espérance mathématique :
1)M(C)=C, où C est une valeur constante ;
2) M (C X) \u003d C M (X),
3)M(X±Y)=M(X)±M(Y);
4)M(X Y)=M(X) M(Y), où X, Y sont des variables aléatoires indépendantes ;
5)M(X±C)=M(X)±C, où C est une valeur constante ;
Pour caractériser le degré de dispersion des valeurs possibles d'une variable aléatoire discrète autour de sa valeur moyenne, on utilise la variance.
Définition: dispersion ré ( X ) la variable aléatoire X est l'espérance mathématique de l'écart au carré de la variable aléatoire par rapport à son espérance mathématique :
Propriétés de dispersion :
1) D(C)=0, où C est une valeur constante ;
2)D(X)>0, où X est une variable aléatoire ;
3) D(C X) = C2 D(X), où C est une valeur constante ;
4)D(X+Y)=D(X)+D(Y), où X, Y sont des variables aléatoires indépendantes ;
Pour calculer la variance, il est souvent pratique d'utiliser la formule :
D(X)=M(X2)-(M(X))2,
où М(Х)=∑ xi2рi= x12р1 + x22р2+…+ xn2рn
La variance D(X) a la dimension du carré d'une variable aléatoire, ce qui n'est pas toujours commode. Par conséquent, la valeur √D(X) est également utilisée comme indicateur de la dispersion des valeurs possibles d'une variable aléatoire.
Définition: Écart-type σ(X) la variable aléatoire X est appelée racine carrée de la variance :
Tâche numéro 2. La variable aléatoire discrète X est donnée par la loi de distribution :
Trouvez P2, la fonction de distribution F(x) et tracez son graphique, ainsi que M(X), D(X), σ(X).
La solution: Puisque la somme des probabilités des valeurs possibles de la variable aléatoire X est égale à 1, alors
Р2=1- (0.1+0.3+0.2+0.3)=0.1
Trouver la fonction de distribution F(x)=P(X Géométriquement, cette égalité peut être interprétée comme suit : F(x) est la probabilité qu'une variable aléatoire prenne la valeur représentée sur l'axe des réels par un point à gauche de x. Si x≤-1, alors F(x)=0, puisqu'il n'y a pas une seule valeur de cette variable aléatoire sur (-∞;x) ; Si -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; Si 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;х) deux valeurs x1=-1 et x2=0 tombent ; Si 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Si 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Si x>3, alors F(x)=P(X=-1) + P(X=0)+ P(X=1)+ P(X=2)+P(X=3)= 0,1 +0,1 +0.3+0.2+0.3=1, puisque quatre valeurs x1=-1, x2=0,x3=1,x4=2 tombent dans l'intervalle (-∞;x) et x5=3. https://pandia.ru/text/78/455/images/image006_89.gif" width="14 height=2" height="2"> 0 pour x≤-1, 0,1 à -1<х≤0, 0,2 à 0<х≤1, F(x)= 0,5 à 1<х≤2, 0,7 à 2<х≤3, 1 pour x>3 Représentons graphiquement la fonction F(x) (Fig. 3) : https://pandia.ru/text/78/455/images/image014_24.jpg" width="158 height=29" height="29">≈1.2845. §
4. Loi de distribution binomiale variable aléatoire discrète, loi de Poisson. Définition: Binôme
appelée loi de distribution d'une variable aléatoire discrète X - le nombre d'occurrences de l'événement A dans n essais répétés indépendants, dans chacun desquels l'événement A peut se produire avec probabilité p ou ne pas se produire avec probabilité q = 1-p. Alors Р(Х=m)-probabilité d'occurrence de l'événement A exactement m fois dans n essais est calculée par la formule de Bernoulli : P(X=m)=Сmnpmqn-m Espérance mathématique, variance et moyenne écart-type une variable aléatoire X distribuée selon une loi binaire se trouve, respectivement, par les formules : https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> La probabilité de l'événement A - "obtenir cinq" dans chaque test est la même et égale à 1/6, c'est-à-dire P(A)=p=1/6, alors P(A)=1-p=q=5/6, où - "les gouttes ne sont pas cinq." La variable aléatoire X peut prendre les valeurs : 0;1;2;3. On trouve la probabilité de chacune des valeurs possibles de X à l'aide de la formule de Bernoulli : P(X=0)=P3(0)=C03p0q3=1 (1/6)0 (5/6)3=125/216 ; P(X=1)=P3(1)=C13p1q2=3 (1/6)1 (5/6)2=75/216 ; P(X=2)=P3(2)=C23p2q=3(1/6)2(5/6)1=15/216 ; P(X=3)=P3(3)=C33p3q0=1 (1/6)3 (5/6)0=1/216. Ce. la loi de distribution de la variable aléatoire X a la forme : Contrôle : 125/216+75/216+15/216+1/216=1. Trouvons les caractéristiques numériques de la variable aléatoire X : M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, Tâche numéro 4. La machine automatique emboutit les pièces. La probabilité qu'une pièce fabriquée soit défectueuse est de 0,002. Trouver la probabilité que parmi 1000 pièces sélectionnées il y ait : a) 5 défectueux ; b) au moins un est défectueux. La solution:
Le nombre n=1000 est grand, la probabilité de fabriquer une pièce défectueuse p=0,002 est faible, et les événements considérés (la pièce sera défectueuse) sont indépendants, donc la formule de Poisson a lieu : Рn(m)= e-
λ
λm Trouvons λ=np=1000 0.002=2. a) Trouvez la probabilité qu'il y ait 5 pièces défectueuses (m=5) : P1000(5)= e-2
25
= 32 0,13534
= 0,0361 b) Trouvez la probabilité qu'il y ait au moins une pièce défectueuse. L'événement A - "au moins une des pièces sélectionnées est défectueuse" est le contraire de l'événement - "toutes les pièces sélectionnées ne sont pas défectueuses". Par conséquent, P (A) \u003d 1-P (). La probabilité souhaitée est donc égale à : Р(А)=1-Р1000(0)=1- e-2
20
\u003d 1-e-2 \u003d 1-0,13534≈0,865. Tâches pour un travail indépendant.
1.1
1.2.
La variable aléatoire dispersée X est donnée par la loi de distribution : Trouvez p4, la fonction de répartition F(X) et tracez son graphique, ainsi que M(X), D(X), σ(X). 1.3.
Il y a 9 feutres dans la boîte dont 2 n'écrivent plus. Au hasard, prenez 3 feutres. Variable aléatoire X - le nombre de feutres d'écriture parmi ceux pris. Composer la loi de distribution d'une variable aléatoire. 1.4.
Il y a 6 manuels placés au hasard sur l'étagère de la bibliothèque, 4 d'entre eux sont reliés. Le bibliothécaire prend 4 manuels au hasard. La variable aléatoire X est le nombre de manuels reliés parmi ceux retenus. Composer la loi de distribution d'une variable aléatoire. 1.5.
Le ticket a deux tâches. Probabilité bonne décision la première tâche est égale à 0,9, la seconde à 0,7. La variable aléatoire X est le nombre de problèmes correctement résolus dans le ticket. Composez une loi de distribution, calculez l'espérance mathématique et la variance de cette variable aléatoire, puis trouvez la fonction de distribution F (x) et construisez son graphique. 1.6.
Trois tireurs tirent sur une cible. La probabilité d'atteindre la cible d'un seul coup pour le premier tireur est de 0,5, pour le second - 0,8, pour le troisième - 0,7. La variable aléatoire X est le nombre de coups sur la cible si les tireurs font un tir chacun. Trouvez la loi de distribution, M(X),D(X). 1.7.
Un basketteur lance le ballon dans le panier avec une probabilité de toucher à chaque lancer de 0,8. Pour chaque touche, il reçoit 10 points, et en cas d'échec, il ne reçoit pas de points. Composez la loi de distribution d'une variable aléatoire X-nombre de points reçus par un basketteur pour 3 lancers. Trouvez M(X),D(X) et aussi la probabilité qu'il obtienne plus de 10 points. 1.8.
Des lettres sont écrites sur les cartes, seulement 5 voyelles et 3 consonnes. 3 cartes sont choisies au hasard, et à chaque fois la carte prise est rendue. La variable aléatoire X est le nombre de voyelles parmi celles prises. Composez une loi de distribution et trouvez M(X),D(X),σ(X). 1.9.
En moyenne, 60 % des contrats Compagnie d'assurance paie les sommes assurées en rapport avec la survenance d'un événement assuré. Compilez la loi de distribution de la variable aléatoire X - le nombre de contrats pour lesquels la somme assurée a été versée parmi quatre contrats sélectionnés au hasard. Trouver les caractéristiques numériques de cette quantité. 1.10.
La station de radio envoie à certains intervalles des indicatifs d'appel (pas plus de quatre) jusqu'à ce que la communication bidirectionnelle soit établie. La probabilité de recevoir une réponse à un indicatif d'appel est de 0,3. Variable aléatoire X-nombre d'indicatifs envoyés. Composez la loi de distribution et trouvez F(x). 1.11.
Il y a 3 clés, dont une seule correspond à la serrure. Établissez une loi de distribution pour la variable aléatoire X-nombre de tentatives d'ouverture de la serrure, si la clé essayée ne participe pas aux tentatives suivantes. Trouver M(X),D(X). 1.12.
Des tests indépendants séquentiels de trois appareils pour la fiabilité sont effectués. Chaque appareil suivant testé uniquement si le précédent s'est avéré fiable. La probabilité de réussir le test pour chaque instrument est de 0,9. Compiler la loi de distribution de la variable aléatoire X-nombre d'appareils testés. 1.13
.La variable aléatoire discrète X a trois valeurs possibles : x1=1, x2, x3 et x1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
Le bloc du dispositif électronique contient 100 éléments identiques. La probabilité de défaillance de chaque élément pendant le temps T est égale à 0,002. Les éléments fonctionnent indépendamment. Trouvez la probabilité que pas plus de deux éléments ne tombent en panne en un temps T. 1.15.
Le manuel a été publié à 50 000 exemplaires. La probabilité que le manuel soit mal relié est de 0,0002. Trouver la probabilité que la circulation contienne : a) quatre livres défectueux, b) moins de deux livres défectueux. 1
.16.
Le nombre d'appels arrivant au PBX chaque minute est distribué selon la loi de Poisson avec le paramètre λ=1.5. Trouver la probabilité que dans une minute il y ait : a) deux appels ; b) au moins un appel. 1.17.
Trouver M(Z),D(Z) si Z=3X+Y. 1.18.
Les lois de distribution de deux variables aléatoires indépendantes sont données : Trouver M(Z),D(Z) si Z=X+2Y. Réponses:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110"> 1.1.
p3=0,4 ; 0 pour x≤-2, 0,3 à -2<х≤0, F(x)= 0,5 à 0<х≤2, 0,9 à 2<х≤5, 1 pour x>5 0,3 à -1<х≤0, 0,4 à 0<х≤1, F(x)= 0,6 à 1<х≤2, 0,7 à 2<х≤3, 1 pour x>3 M(X) = 1 ; D(X) = 2,6 ; σ(X) ≈1,612. https://pandia.ru/text/78/455/images/image025_24.gif" width="2 height=98" height="98"> 0 pour x≤0, 0,03 à 0<х≤1, F(x)= 0,37 à 1<х≤2, 1 pour x>2 M(X)=2 ; D(X)=0,62 M(X) = 2,4 ; D(X)=0,48, P(X>10)=0,896 1.
8
.
M(X) = 15/8 ; D(X) = 45/64 ; σ(å) ≈ M(X) = 2,4 ; D(X)=0,96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(X)=2 ; D(X)=2/3 1.14.
1.22e-0.2≈0.999 1.15.
a) 0,0189 ; b) 0,00049 1.16.
a) 0,0702 ; b) 0,77687 1.17.
3,8; 14,2 1.18.
11,2; 4. Chapitre 2 Variable aléatoire continue
Définition: Continu
nommez la valeur, dont toutes les valeurs possibles remplissent complètement l'intervalle fini ou infini de l'axe numérique. Évidemment, le nombre de valeurs possibles d'une variable aléatoire continue est infini. Une variable aléatoire continue peut être spécifiée à l'aide d'une fonction de distribution. Définition: F fonction de répartition
la variable aléatoire continue X est la fonction F(x), qui détermine pour chaque valeur xhttps://pandia.ru/text/78/455/images/image028_11.jpg" width="14" height="13">R La fonction de distribution est parfois appelée fonction de distribution cumulative. Propriétés de la fonction de distribution :
1)1≤F(x)≤1 2) Pour une variable aléatoire continue, la fonction de distribution est continue en tout point et différentiable partout, sauf peut-être en des points individuels. 3) La probabilité de toucher une variable aléatoire X dans l'un des intervalles (a; b), [a; b), [a; b], est égale à la différence entre les valeurs de la fonction F (x) aux points a et b, c'est-à-dire Pennsylvanie<Х 4) La probabilité qu'une variable aléatoire continue X prenne une seule valeur est 0. 5) F(-∞)=0, F(+∞)=1 La spécification d'une variable aléatoire continue à l'aide d'une fonction de distribution n'est pas la seule. Introduisons le concept de densité de distribution de probabilité (densité de distribution). Définition
:
Densité de probabilité
F
(
X
)
la variable aléatoire continue X est la dérivée de sa fonction de répartition, soit : La densité de distribution de probabilité est parfois appelée fonction de distribution différentielle ou loi de distribution différentielle. Le graphique de la densité de la distribution de probabilité f(x) est appelé courbe de distribution de probabilité
.
Propriétés de densité de probabilité :
1) f(x) ≥0, quand xhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" height="141">.gif" width="14" hauteur ="62 src="> 0 pour x≤2, f(x)= c(x-2) à 2<х≤6, 0 pour x>6. Trouver : a) la valeur de c ; b) la fonction de distribution F(x) et construire son graphe ; c) Р(3≤х<5) La solution:
+
∞ a) Trouver la valeur de c à partir de la condition de normalisation : ∫ f(x)dx=1. Donc, -∞ https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> -∞ 2 2 x si 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х - (4/2-4))= 1/8(x2/2-2x+2)=1/16(x-2)2 ; Gif" width="14" height="62"> 0 pour x≤2, F (x) \u003d (x-2) 2/16 à 2<х≤6, 1 pour x>6. Le graphique de la fonction F(x) est représenté sur la Fig. 3 https://pandia.ru/text/78/455/images/image034_23.gif" width="14" height="62 src="> 0 pour x≤0, F (x) \u003d (3 arctg x) / π à 0<х≤√3, 1 pour x>√3. Trouver la fonction de distribution différentielle f(x) La solution:
Puisque f (x) \u003d F '(x), alors https://pandia.ru/text/78/455/images/image011_36.jpg" width="118" height="24"> Toutes les propriétés d'espérance mathématique et de dispersion considérées précédemment pour les variables aléatoires dispersées sont également valables pour les variables continues. Tâche numéro 3. La variable aléatoire X est donnée fonction différentielle f(x): https://pandia.ru/text/78/455/images/image036_19.gif" height="38"> -∞ 2 X3/9 + x2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> +∞ D(X)= ∫ x2 f(x)dx-(M(x))2=∫ x2 x/3 dx+∫1/3x2 dx=(31/18)2=x4/12 +x3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. Tâches pour une solution indépendante.
2.1.
Une variable aléatoire continue X est donnée par une fonction de distribution : 0 pour x≤0, F(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 pour x≤ π/6, F(х)= - cos 3x à π/6<х≤ π/3, 1 pour x> π/3. Trouvez la fonction de distribution différentielle f(x) et aussi Р(2π /9<Х< π /2). 2.3.
0 pour x≤2, f(x)= avec x à 2<х≤4, 0 pour x>4. 2.4.
Une variable aléatoire continue X est donnée par la densité de distribution : 0 pour x≤0, f(х)= с √х à 0<х≤1, 0 pour x>1. Trouver : a) le nombre c ; b) M(X), D(X). 2.5.
https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" height="39"> pour x, 0 à x. Trouver : a) F(x) et tracer son graphique ; b) M(X),D(X), σ(X); c) la probabilité que dans quatre tests indépendants la valeur X prendra exactement 2 fois la valeur appartenant à l'intervalle (1; 4). 2.6.
La densité de distribution de probabilité d'une variable aléatoire continue X est donnée : f (x) \u003d 2 (x-2) pour x, 0 à x. Trouver : a) F(x) et tracer son graphique ; b) M(X),D(X), σ(X); c) la probabilité que dans trois tests indépendants la valeur X prenne exactement 2 fois la valeur appartenant à l'intervalle . 2.7.
La fonction f(x) est donnée par : https://pandia.ru/text/78/455/images/image045_4.jpg" width="43" height="38 src=">.jpg" width="16" height="15">[-√ 3/2 ; √3/2]. 2.8.
La fonction f(x) est donnée par : https://pandia.ru/text/78/455/images/image046_5.jpg" width="45" height="36 src="> .jpg" width="16" height="15">[- π /quatre ; π/4]. Trouvez: a) la valeur de la constante c, à laquelle la fonction sera la densité de probabilité d'une variable aléatoire X; b) fonction de répartition F(x). 2.9.
La variable aléatoire Х, concentrée sur l'intervalle (3;7), est donnée par la fonction de répartition F(х)= . Trouvez la probabilité que la variable aléatoire X prendra la valeur : a) inférieure à 5, b) non inférieure à 7. 2.10.
Variable aléatoire X, concentrée sur l'intervalle (-1 ; 4), donnée par la fonction de répartition F(x)= . Trouvez la probabilité que la variable aléatoire X prendra la valeur : a) inférieure à 2, b) non inférieure à 4. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" height="44 src="> .jpg" width="16" height="15">. Trouver : a) le nombre c ; b) M(X); c) probabilité P(X > M(X)). 2.12.
La variable aléatoire est donnée par la fonction de distribution différentielle : https://pandia.ru/text/78/455/images/image050_3.jpg" width="60" height="38 src=">.jpg" width="16 height=15" height="15"> . Trouvez : a) M(X); b) probabilité Р(Х≤М(Х)) 2.13.
La distribution temporelle est donnée par la densité de probabilité : https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" height="37"> pour x ≥0. Montrer que f(x) est bien une distribution de densité de probabilité. 2.14.
La densité de distribution de probabilité d'une variable aléatoire continue X est donnée : https://pandia.ru/text/78/455/images/image054_3.jpg" width="174" height="136 src="> (fig.4) 2.16.
La variable aléatoire X est distribuée selon la loi " triangle rectangle» dans l'intervalle (0;4) (Fig.5). Trouvez une expression analytique pour la densité de probabilité f(x) sur tout l'axe réel. Réponses
0 pour x≤0, f(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 pour x≤ π/6, F(x)= 3sin 3x à π/6<х≤ π/3, 0 pour x > π/3. Une variable aléatoire continue X a loi uniforme distribution sur un certain intervalle (a; b), auquel appartiennent toutes les valeurs possibles de X, si la densité de distribution de probabilité f (x) est constante sur cet intervalle et est égale à 0 en dehors de celui-ci, c'est-à-dire 0 pour x≤a, f(x)= pour un<х 0 pour x≥b. Le graphique de la fonction f(x) est représenté sur la fig. une F(х)= https://pandia.ru/text/78/455/images/image077_3.jpg" width="30" height="37">, D(X)=, σ(Х)=. Tâche numéro 1. La variable aléatoire X est uniformément distribuée sur le segment . Trouver: a) la densité de distribution de probabilité f(x) et construire son graphe ; b) la fonction de distribution F(x) et construire son graphe ; c) M(X),D(X), σ(X). La solution:
En utilisant les formules discutées ci-dessus, avec a=3, b=7, on trouve : https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" height="39"> à 3≤х≤7, 0 pour x>7 Construisons son graphe (Fig. 3) : https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86 src="> 0 pour x≤3, F(х)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" height="119 src=">fig.4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" height="43">==https://pandia.ru/text/ 78/455/images/image092_10.gif" width="14" height="49 src="> 0 pour x<0, f(х)= λе-λх à х≥0. La fonction de distribution d'une variable aléatoire X, distribuée selon une loi exponentielle, est donnée par la formule : https://pandia.ru/text/78/455/images/image094_4.jpg" width="191" height="126 src=">fig..jpg" width="22" height="30"> , D(X)=, σ(X)= Ainsi, l'espérance mathématique et l'écart type de la distribution exponentielle sont égaux l'un à l'autre. La probabilité que X tombe dans l'intervalle (a;b) est calculée par la formule : Р (un<Х Tâche numéro 2. La disponibilité moyenne de l'appareil est de 100 heures. En supposant que la disponibilité de l'appareil a une loi de distribution exponentielle, trouvez : a) densité de distribution de probabilité ; b) fonction de distribution ; c) la probabilité que le temps de fonctionnement sans panne de l'appareil dépasse 120 heures. La solution:
Par condition, la distribution mathématique M(X)=https://pandia.ru/text/78/455/images/image098_10.gif" height="43 src="> 0 pour x<0, a) f(x)= 0,01e -0,01x pour x≥0. b) F(x)= 0 pour x<0, 1-e -0,01x à x≥0. c) Nous trouvons la probabilité souhaitée en utilisant la fonction de distribution : P(X>120)=1-F(120)=1-(1-e-1.2)=e-1.2≈0.3. §
3. Loi de distribution normale Définition:
Une variable aléatoire continue X a loi de distribution normale (loi gaussienne),
si sa densité de distribution est de la forme : où m=M(X), σ2=D(X), σ>0. La courbe de distribution normale est appelée courbe normale ou gaussienne
(fig.7) La fonction de distribution d'une variable aléatoire X, distribuée selon la loi normale, s'exprime par la fonction de Laplace Ф (х) selon la formule : où est la fonction de Laplace. Commentaire:
La fonction Ф(х) est impaire (Ф(-х)=-Ф(х)), de plus, si x>5, on peut considérer Ф(х) ≈1/2. Le graphique de la fonction de distribution F(x) est représenté sur la fig. huit https://pandia.ru/text/78/455/images/image106_4.jpg" width="218" height="33"> La probabilité que valeur absolue les écarts sont moindres nombre positifδ est calculé par la formule : En particulier, pour m=0 l'égalité est vraie : "Règle des trois sigma"
Si une variable aléatoire X a une loi de distribution normale de paramètres m et σ, alors il est pratiquement certain que sa valeur est comprise dans l'intervalle (a-3σ ; a+3σ), car https://pandia.ru/text/78/455/images/image110_2.jpg" width="157" height="57 src=">a) b) Utilisons la formule : https://pandia.ru/text/78/455/images/image112_2.jpg" width="369" height="38 src="> Selon le tableau des valeurs de la fonction Ф(х) on trouve Ф(1.5)=0.4332, Ф(1)=0.3413. La probabilité recherchée est donc : P(28 Tâches pour le travail indépendant
3.1.
La variable aléatoire X est uniformément distribuée dans l'intervalle (-3;5). Trouver: b) fonction de distribution F(x); c) caractéristiques numériques ; d) probabilité P(4<х<6). 3.2.
La variable aléatoire X est uniformément distribuée sur le segment . Trouver: a) densité de distribution f(x); b) fonction de distribution F(x); c) caractéristiques numériques ; d) probabilité Р(3≤х≤6). 3.3.
Un feu de signalisation automatique est installé sur l'autoroute, dans lequel le feu vert est allumé pendant 2 minutes pour les véhicules, jaune pendant 3 secondes et rouge pendant 30 secondes, etc. La voiture passe le long de l'autoroute à une heure aléatoire. Trouvez la probabilité que la voiture passe le feu sans s'arrêter. 3.4.
Les rames de métro circulent régulièrement à des intervalles de 2 minutes. Le passager entre sur le quai à un moment aléatoire. Quelle est la probabilité que le passager doive attendre plus de 50 secondes pour le train ? Trouvez l'espérance mathématique d'une variable aléatoire X - le temps d'attente du train. 3.5.
Trouvez la variance et l'écart type de la distribution exponentielle donnée par la fonction de distribution : F(x)= 0 à x<0, 1-e-8x pour x≥0. 3.6.
Une variable aléatoire continue X est donnée par la densité de distribution de probabilité : f(x)=0 à x<0, 0,7 e-0,7x à x≥0. a) Nommez la loi de distribution de la variable aléatoire considérée. b) Trouver la fonction de répartition F(X) et les caractéristiques numériques de la variable aléatoire X. 3.7.
La variable aléatoire X est distribuée selon la loi exponentielle, donnée par la densité de distribution de probabilité : f(x)=0 à x<0, 0,4 e-0,4 x à x≥0. Trouvez la probabilité qu'à la suite du test, X prenne une valeur de l'intervalle (2,5 ; 5). 3.8.
Une variable aléatoire continue X est distribuée selon la loi exponentielle donnée par la fonction de distribution : F(x)= 0 à x<0, 1er-0,6x à x≥0 Trouvez la probabilité qu'à la suite du test, X prenne une valeur de l'intervalle . 3.9.
L'espérance mathématique et l'écart type d'une variable aléatoire normalement distribuée sont respectivement 8 et 2. a) densité de distribution f(x); b) la probabilité que, à la suite du test, X prenne une valeur de l'intervalle (10;14). 3.10.
La variable aléatoire X est normalement distribuée avec une moyenne de 3,5 et une variance de 0,04. Trouver: a) densité de distribution f(x); b) la probabilité que, à la suite du test, X prenne une valeur de l'intervalle . 3.11.
La variable aléatoire X est normalement distribuée avec M(X)=0 et D(X)=1. Lequel des événements : |X|≤0,6 ou |X|≥0,6 a une probabilité plus élevée ? 3.12.
La variable aléatoire X est normalement distribuée avec M(X) = 0 et D(X) = 1. À partir de quel intervalle (-0,5 ; -0,1) ou (1 ;2) dans un essai prendra-t-elle une valeur avec une probabilité plus élevée ? 3.13.
Le prix actuel par action peut être modélisé à l'aide d'une distribution normale avec M(X)=10den. unités et σ (X) = 0,3 den. unités Trouver: a) la probabilité que le cours actuel de l'action soit de 9,8 den. unités jusqu'à 10,4 deniers. unités; b) en utilisant la "règle de trois sigma" pour trouver les limites dans lesquelles se situera le prix actuel de l'action. 3.14.
La substance est pesée sans erreurs systématiques. Les erreurs de pesée aléatoires sont soumises à la loi normale avec le rapport racine-carré σ=5r. Trouver la probabilité que dans quatre expériences indépendantes l'erreur dans trois pesées ne se produise pas en valeur absolue 3r. 3.15.
La variable aléatoire X est normalement distribuée avec M(X)=12,6. La probabilité qu'une variable aléatoire tombe dans l'intervalle (11,4 ; 13,8) est de 0,6826. Trouvez l'écart type σ. 3.16.
La variable aléatoire X est normalement distribuée avec M(X) = 12 et D(X) = 36. Trouvez l'intervalle dans lequel, avec une probabilité de 0,9973, la variable aléatoire X tombe à la suite du test. 3.17.
Une pièce fabriquée par une machine automatique est considérée comme défectueuse si l'écart X de son paramètre contrôlé par rapport à la valeur nominale dépasse 2 unités de mesure modulo. On suppose que la variable aléatoire X est normalement distribuée avec M(X)=0 et σ(X)=0,7. Quel pourcentage de pièces défectueuses la machine donne-t-elle ? 3.18.
Le paramètre de détail X est normalement distribué avec une espérance mathématique de 2 égale à la valeur nominale et un écart type de 0,014. Trouvez la probabilité que l'écart de X par rapport au modulo de la valeur nominale ne dépasse pas 1 % de la valeur nominale. Réponses
https://pandia.ru/text/78/455/images/image116_9.gif" width="14" height="110 src="> b) 0 pour x≤-3, F(x)=gauche"> 3.10.
a)f(x)= , b) Р(3.1≤Х≤3.7) ≈0.8185. 3.11.
|x|≥0.6. 3.12.
(-0,5;-0,1). 3.13.
a) Р(9.8≤Х≤10.4) ≈0.6562. 3.14.
0,111. 3.15.
σ=1,2. 3.16.
(-6;30). 3.17.
0,4%. Loi de distribution d'une variable aléatoire X : Exemple #2. La probabilité d'atteindre la cible par un tireur avec un coup pour le premier tireur est de 0,8, pour le deuxième tireur - 0,85. Les tireurs ont tiré un coup sur la cible. En supposant que les tireurs individuels atteignent la cible en tant qu'événements indépendants, trouvez la probabilité de l'événement A - exactement un coup sur la cible. Variable aléatoire
est appelée une variable qui peut prendre certaines valeurs en fonction de diverses circonstances, et à son tour, une variable aléatoire est appelée discret
si l'ensemble de ses valeurs est fini ou dénombrable. En plus des variables aléatoires discrètes, il existe également des variables aléatoires continues. Examinons plus en détail le concept de variable aléatoire. En pratique, il y a souvent des grandeurs qui peuvent prendre certaines valeurs, mais il est impossible de prédire de manière fiable quelle valeur chacune d'elles prendra dans l'expérience, le phénomène, l'observation considérée. Par exemple, le nombre de garçons qui naîtront à Moscou le lendemain peut être différent. Il peut être égal à zéro (pas un seul garçon ne naîtra : toutes les filles naîtront ou il n'y aura pas de nouveau-nés du tout), un, deux, et ainsi de suite jusqu'à un nombre fini n. Ces valeurs incluent: la masse de racines de betterave à sucre sur le site, la portée de vol d'un obus d'artillerie, le nombre de pièces défectueuses dans un lot, etc. De telles valeurs seront appelées aléatoires. Ils caractérisent tous les résultats possibles d'une expérience ou d'une observation d'un point de vue quantitatif. Exemples de variables aléatoires discrètes
avec un nombre fini de valeurs, le nombre d'enfants nés pendant la journée dans une colonie, le nombre de passagers de bus, le nombre de passagers transportés par le métro de Moscou par jour, etc. peuvent servir. Le nombre de valeurs d'une variable aléatoire discrète peut être infini, mais c'est un ensemble dénombrable. Mais dans tous les cas, ils peuvent être numérotés dans un certain ordre, ou, plus précisément, une correspondance biunivoque peut être établie entre les valeurs d'une variable aléatoire et les nombres naturels 1, 2, 3, ..., n. Attention : un nouveau concept très important de la théorie des probabilités - droit de la distribution
. Laisser X peut prendre n valeurs: . Nous supposerons qu'ils sont tous différents (sinon les mêmes doivent être combinés) et classés par ordre croissant. Pour une caractérisation complète d'une variable aléatoire discrète doit être donnée non seulement toutes ses valeurs, mais aussi les probabilités
La loi de distribution d'une variable aléatoire discrète
toute règle (fonction, table) est appelée p(X), qui vous permet de trouver les probabilités de toutes sortes d'événements associés à une variable aléatoire (par exemple, la probabilité qu'il s'agisse d'un exemple d'une certaine valeur ou qu'il tombe dans un intervalle). La loi de distribution la plus simple et la plus pratique pour une variable aléatoire discrète est donnée sous la forme du tableau suivant : Un tel tableau s'appelle près de la distribution d'une variable aléatoire discrète. La ligne du haut de la série de distribution répertorie par ordre croissant toutes les valeurs possibles d'une variable aléatoire discrète (x), et la ligne du bas répertorie les probabilités de ces valeurs ( p). Développements Exemple 1 Une loterie a été organisée dans le groupe étudiant. Deux choses d'une valeur de 1000 roubles sont jouées. et un coûtant 3000 roubles. Élaborez la loi de répartition du montant des gains nets pour un étudiant qui a acheté un billet pour 100 roubles. Au total, 50 billets ont été vendus. La solution. La variable aléatoire qui nous intéresse X peut prendre trois valeurs : - 100 roubles. (si l'étudiant ne gagne pas, mais perd en fait les 100 roubles qu'il a payés pour le billet), 900 roubles. et 2900 roubles. (les gains réels sont réduits de 100 roubles - le coût du billet). Le premier résultat est favorisé par 47 cas sur 50, le deuxième par 2 et le troisième par un. Leurs probabilités sont donc : P(X=-100)=47/50=0,94
,
P(X=900)=2/50=0,04
,
P(X=2900)=1/50=0,02
. Loi de distribution d'une variable aléatoire discrète X a la forme Une série de distribution ne peut être construite que pour une variable aléatoire discrète (pour une non discrète, elle ne peut pas être construite, ne serait-ce que parce que l'ensemble des valeurs possibles d'une telle variable aléatoire est indénombrable, elles ne peuvent pas être listées en haut ligne du tableau). La forme la plus générale de la loi de distribution, adaptée à toutes les variables aléatoires (discrètes et non discrètes), est la fonction de distribution. La fonction de distribution d'une variable aléatoire discrète ou fonction intégrale appelé une fonction La fonction de distribution de toute variable aléatoire discrète est une fonction échelon discontinue dont les sauts se produisent aux points correspondant aux valeurs possibles de la variable aléatoire et sont égaux aux probabilités de ces valeurs. Exemple 2 Variable aléatoire discrète X est le nombre de points marqués en lançant un dé. Construire sa fonction de distribution. La solution. Série de distribution d'une variable aléatoire discrète X ressemble à: fonction de répartition F(X) a 6 sauts égaux en magnitude à 1/6 (dans la figure ci-dessous). Exemple 3 Une urne contient 6 boules blanches et 4 boules noires. 3 boules sont extraites de l'urne. Le nombre de boules blanches parmi les boules tirées est une variable aléatoire discrète X. Composez la loi de distribution qui lui correspond. X peut prendre les valeurs 0, 1, 2, 3. Les probabilités qui leur correspondent peuvent être plus facilement calculées à partir de règle de multiplication des probabilités. On obtient la loi de distribution suivante pour une variable aléatoire discrète : Exemple 4 Composez une loi de distribution pour une variable aléatoire discrète - le nombre de coups sur la cible avec quatre coups, si la probabilité de toucher avec un coup est de 0,1. La solution. Variable aléatoire discrète X peut prendre cinq valeurs différentes : 1, 2, 3, 4, 5. On trouve les probabilités correspondantes à partir de Formule de Bernoulli
n = 4
, p = 1,1
, q = 1 - p = 0,9
, m = 0, 1, 2, 3, 4
on a Par conséquent, la loi de distribution d'une variable aléatoire discrète X a la forme Si les probabilités des valeurs d'une variable aléatoire discrète peuvent être déterminées par la formule de Bernoulli, alors la variable aléatoire a distribution binomiale . Si le nombre d'essais est suffisamment grand, alors la probabilité que dans ces essais l'événement d'intérêt se produise exactement m temps, respecte la loi Loi de Poisson . Pour calculer la fonction de distribution d'une variable aléatoire discrète F(X), il est nécessaire d'ajouter les probabilités de toutes les valeurs inférieures ou égales à la valeur limite X. Exemple 5 Le tableau contient des données sur la dépendance du nombre de mariages dissous au cours de l'année à la durée du mariage. Trouvez la probabilité que le prochain mariage divorcé ait duré moins de ou égal à 5 ans. La solution. Les probabilités sont calculées en divisant le nombre de mariages divorcés pertinents par le nombre total de 6010. La probabilité que le prochain mariage divorcé ait duré 5 ans est de 0,056. La probabilité que la durée du prochain mariage divorcé soit inférieure ou égale à 5 ans est égale à 0,186. Nous l'avons obtenu en ajoutant à la valeur F(X) pour les mariages d'une durée de 4 ans inclus, la probabilité pour les mariages d'une durée de 5 ans. Souvent, toutes les valeurs d'une variable aléatoire discrète ne sont pas connues, mais certaines valeurs ou probabilités de la série sont connues, et aussi espérance mathématique et (ou) variance d'une variable aléatoire auquel une leçon séparée est consacrée. Voici quelques formules de cette leçon qui peuvent aider à établir la loi de distribution d'une variable aléatoire discrète et à analyser des exemples de résolution de tels problèmes. L'espérance mathématique d'une variable aléatoire discrète est la somme des produits de toutes ses valeurs possibles et des probabilités de ces valeurs : La formule de dispersion d'une variable aléatoire discrète est par définition : Souvent, la formule de variance suivante est plus pratique pour les calculs : où Exemple 6 Variable aléatoire discrète X ne peut prendre que deux valeurs. Il prend la plus petite valeur avec probabilité p= 0,6. Trouver la loi de distribution d'une variable aléatoire discrète X, si l'on sait que son espérance mathématique et sa variance sont . La solution. La probabilité qu'une variable aléatoire prenne une valeur plus grande X2
, est égal à 1 − 0,6 = 4 . En utilisant la formule (1) de l'espérance mathématique, nous allons composer une équation dans laquelle les inconnues sont les valeurs de notre variable aléatoire discrète : En utilisant la formule (2) de la dispersion, on compose une autre équation dans laquelle les inconnues sont aussi les valeurs d'une variable aléatoire discrète : Le système de deux équations obtenues résoudre par la méthode de substitution. De la première équation on obtient En substituant cette expression dans la seconde équation, après de simples transformations, on obtient équation quadratique qui a deux racines : 7/5 et −1 . La première racine ne remplit pas les conditions du problème, puisque X2
< X 1
. Ainsi, les valeurs que peut prendre une variable aléatoire discrète X selon les conditions de notre exemple, sont égaux X1
= −1
et X2
= 2
. Une série de distribution d'une variable aléatoire discrète est donnée. Trouvez la probabilité manquante et tracez la fonction de distribution. Calculez l'espérance mathématique et la variance de cette valeur. La variable aléatoire X ne prend que quatre valeurs : -4, -3, 1 et 2. Elle prend chacune de ces valeurs avec une certaine probabilité. Puisque la somme de toutes les probabilités doit être égale à 1, la probabilité manquante est égale à : 0,3 + ? + 0,1 + 0,4 = 1, Composez la fonction de distribution de la variable aléatoire X. On sait que la fonction de distribution , alors : Par conséquent, Traçons la fonction F(X)
. L'espérance mathématique d'une variable aléatoire discrète est égale à la somme des produits de la valeur de la variable aléatoire et de la probabilité correspondante, c'est-à-dire La variance d'une variable aléatoire discrète est trouvée par la formule : Ici : - factorielle d'un nombre Un événement est tout fait qui peut ou non se produire à la suite d'une expérience. Fusionner des événements MAIS et À- cet evènement DE, qui consiste en l'apparition ou l'événement MAIS, ou événements À, ou les deux événements en même temps. La désignation: Croisement d'événements MAIS et À- cet evènement DE, qui consiste en la survenance simultanée des deux événements. La désignation: Probabilité d'événement MAIS est le rapport du nombre d'expériences Probabilité d'événement Si les événements A et B sont indépendants (l'occurrence de l'un n'affecte pas l'occurrence de l'autre), alors la probabilité de l'événement est : Probabilité d'événement Probabilité d'événement MAIS, Probabilité d'événement À, Si les événements A et B sont incompatibles (ils ne peuvent pas se produire en même temps), alors la probabilité de l'événement est : Laissez l'événement MAIS peut se produire simultanément avec l'un des événements Soit n tests indépendants effectués. Probabilité d'occurrence (succès) d'un événement MAIS en chacun d'eux est constante et égale p, la probabilité de défaillance (c'est-à-dire pas la survenance d'un événement MAIS) q
=
1 - p. Alors la probabilité d'occurrence k succès dans n les tests peuvent être trouvés par la formule de Bernoulli : Nombre de succès le plus probable discret continu (par exemple, nombre de filles dans une famille de 5 enfants) (par exemple, disponibilité de la bouilloire) Soit la valeur discrète donnée par une série de distribution : , , …, - valeurs d'une variable aléatoire X; , , …, sont les probabilités correspondantes. La fonction de distribution d'une variable aléatoire X est appelée une fonction donnée sur toute la droite numérique et égale à la probabilité que X sera moins X: Événement. Opérations sur événements aléatoires. Le concept de la probabilité d'un événement. Règles d'addition et de multiplication des probabilités. Probabilités conditionnelles. Formule de probabilité totale. Formule de Bayes. Schéma de Bernoulli. Variable aléatoire, sa fonction de distribution et sa série de distribution. Propriétés de base de la fonction de distribution. Valeur attendue. Propriétés de l'espérance mathématique. Dispersion. Propriétés de dispersion. Densité de distribution de probabilité d'une variable aléatoire unidimensionnelle. Types de distributions : uniforme, exponentielle, normale, binomiale et distribution de Poisson. Théorèmes locaux et intégraux de Moivre-Laplace. Loi et fonction de distribution d'un système de deux variables aléatoires. Densité de distribution d'un système de deux variables aléatoires. Lois conditionnelles de distribution, espérance mathématique conditionnelle. Variables aléatoires dépendantes et indépendantes. Coefficient de corrélation. Goûter. Traitement des échantillons. Histogramme de polygone et de fréquence. Fonction de distribution empirique. Le concept d'estimation des paramètres de distribution. Exigences d'évaluation. Intervalle de confiance. Construire des intervalles pour estimer l'espérance mathématique et l'écart type. hypothèses statistiques. Critères de consentement. Dans les applications de la théorie des probabilités, la caractérisation quantitative de l'expérience est de première importance. Une quantité qui peut être déterminée quantitativement et qui, à la suite d'une expérience, peut prendre des valeurs différentes selon les cas, est appelée une variable aléatoire. Exemples de variables aléatoires : 1. Le nombre d'occurrences d'un nombre pair de points en dix lancers de dés. 2. Le nombre de touches sur la cible par le tireur qui tire une série de coups. 3. Le nombre de fragments d'un projectile qui explose. Dans chacun des exemples ci-dessus, une variable aléatoire ne peut prendre que des valeurs isolées, c'est-à-dire des valeurs qui peuvent être énumérées à l'aide d'une série naturelle de nombres. Une telle variable aléatoire, dont les valeurs possibles sont des nombres isolés séparés que cette variable prend avec certaines probabilités, est appelée discret. Le nombre de valeurs possibles d'une variable aléatoire discrète peut être fini ou infini (dénombrable). droit de la distribution Une variable aléatoire discrète est appelée une liste de ses valeurs possibles et de leurs probabilités correspondantes. La loi de distribution d'une variable aléatoire discrète peut être spécifiée sous forme de tableau (série de distribution de probabilité), analytiquement et graphiquement (polygone de distribution de probabilité). Lors de la réalisation de telle ou telle expérience, il devient nécessaire d'évaluer la valeur étudiée "en moyenne". Le rôle de la valeur moyenne d'une variable aléatoire est joué par une caractéristique numérique appelée espérance mathématique, qui est défini par la formule où X 1 , X 2
,.. , X n– valeurs d'une variable aléatoire X, un p 1 ,p 2 ,
... , p n sont les probabilités de ces valeurs (notez que p 1
+
p 2
+…+
p n =
1). Exemple. Le tir est effectué sur la cible (Fig. 11). Un coup sûr en I donne trois points, en II - deux points, en III - un point. Le nombre de points assommés avec un tir par un tireur a une loi de distribution de la forme Pour comparer l'habileté des tireurs, il suffit de comparer les valeurs moyennes des points marqués, c'est-à-dire attentes mathématiques M(X) et M(Oui):
M(X)
=
1
0,4
+ 2
0,2
+ 3
0,4
= 2,0, M(Oui)
=
1
0,2
+ 2
0,5
+ 3
0,3
= 2,1. Le deuxième tireur donne en moyenne un nombre de points légèrement supérieur, c'est-à-dire avec des prises de vue répétées, cela donnera le meilleur résultat. Notez les propriétés de l'espérance mathématique : 1. L'espérance mathématique d'une valeur constante est égale à la constante elle-même : M(C)
=C. 2. L'espérance mathématique de la somme des variables aléatoires est égale à la somme des espérances mathématiques des termes : M=(X 1 +
X 2 +…+
X n)=
M(X 1)+
M(X 2)+…+
M(X n). 3. L'espérance mathématique du produit de variables aléatoires mutuellement indépendantes est égale au produit des espérances mathématiques des facteurs M(X 1 X 2 …
X n)
=
M(X 1)M(X 2)…
M(X n). 4. La négation mathématique de la distribution binomiale est égale au produit du nombre d'essais et de la probabilité qu'un événement se produise dans un essai (tâche 4.6). M(X)
= pr. Pour évaluer comment une variable aléatoire s'écarte "en moyenne" de son espérance mathématique, c'est-à-dire afin de caractériser la dispersion des valeurs d'une variable aléatoire en théorie des probabilités, le concept de dispersion est utilisé. dispersion Variable aléatoire X s'appelle l'espérance mathématique de l'écart au carré : ré(X)
=
M[(X
-
M(X)) 2 ]. La dispersion est une caractéristique numérique de la dispersion d'une variable aléatoire. On peut voir à partir de la définition que plus la dispersion d'une variable aléatoire est petite, plus ses valeurs possibles sont proches de l'espérance mathématique, c'est-à-dire que mieux les valeurs de la variable aléatoire sont caractérisées par son mathématique attente. Il découle de la définition que la variance peut être calculée par la formule Il est commode de calculer la dispersion en utilisant une autre formule : ré(X)
=
M(X 2)
- (M(X)) 2 .
La dispersion a les propriétés suivantes : 1. La dispersion de la constante est nulle : ré(C)
=
0.
2. Un facteur constant peut être extrait du signe de dispersion en le mettant au carré : ré(CX)
=
C 2 ré(X). 3. La variance de la somme des variables aléatoires indépendantes est égale à la somme de la variance des termes : ré(X 1 +
X 2 +
X 3 +…+
X n)=
ré(X 1)+
ré(X 2)+…+
ré(X n) 4. La variance de la distribution binomiale est égale au produit du nombre d'essais par la probabilité d'occurrence et de non-occurrence d'un événement dans un essai : ré(X)
= npq. En théorie des probabilités, on utilise souvent une caractéristique numérique, égale à la racine carrée de la variance d'une variable aléatoire. Cette caractéristique numérique est appelée écart-type et est désignée par le symbole Il caractérise la taille approximative de l'écart d'une variable aléatoire par rapport à sa valeur moyenne et a la même dimension que la variable aléatoire. 4.1.
Le tireur tire trois coups sur la cible. La probabilité d'atteindre la cible à chaque tir est de 0,3. Construisez une série de distribution du nombre de résultats. La solution. Le nombre de résultats est une variable aléatoire discrète X. Chaque valeur X n
Variable aléatoire X correspond à une certaine probabilité P n . La loi de distribution d'une variable aléatoire discrète dans ce cas peut être définie près de la distribution. Dans cette tâche X prend les valeurs 0, 1, 2, 3. Selon la formule de Bernoulli trouver les probabilités des valeurs possibles de la variable aléatoire : R 3 (0)
= (0,7) 3 =
0,343, R 3 (1)
= R 3 (2)
= R 3 (3)
= (0,3) 3 =
0,027. Après avoir arrangé les valeurs de la variable aléatoire X dans l'ordre croissant, on obtient la série de distribution : X n A noter que la somme désigne la probabilité que la variable aléatoire X prendra au moins une valeur parmi les possibles, et cet événement est certain, donc 4.2
.Il y a quatre boules dans l'urne, numérotées de 1 à 4. Deux boules sont sorties. Valeur aléatoire X est la somme des nombres de boules. Construire une série de distribution d'une variable aléatoire X. La solution. Valeurs d'une variable aléatoire X sont 3, 4, 5, 6, 7. Trouvez les probabilités correspondantes. Valeur 3 variable aléatoire X peut prendre dans le seul cas où l'une des boules sélectionnées a le numéro 1 et l'autre 2. Le nombre de résultats possibles du test est égal au nombre de combinaisons de quatre (le nombre de paires de boules possibles) par deux. D'après la formule de probabilité classique, on obtient De même, R(X= 4) =R(X= 6) =R(X= 7) = 1/6. La somme 5 peut apparaître dans deux cas : 1 + 4 et 2 + 3, donc X ressemble à: Trouver la fonction de distribution F(X) Variable aléatoire X et tracez-le. Calculer pour X son espérance mathématique et sa variance. La solution. La loi de distribution d'une variable aléatoire peut être donnée par la fonction de distribution F(X)
=P(X
X).
fonction de répartition F(X) est une fonction continue à gauche non décroissante définie sur tout l'axe réel, tandis que F
(-
)=
0,F
(+
)=
1. Pour une variable aléatoire discrète, cette fonction est exprimée par la formule Par conséquent, dans ce cas Tracé de la fonction de distribution F(X) est une ligne en escalier (Fig. 12) F(X) Valeur attendueM(X) est la moyenne pondérée des valeurs X 1 , X 2 ,……X n Variable aléatoire X avec des poids ρ
1,
ρ
2, ……
, ρ
n
et est appelée la valeur moyenne de la variable aléatoire X. Selon la formule M(X)=x 1
ρ
1 +x 2
ρ
2 + ……+x n
ρ
n M(X) = 3 0,14 + 5 0,2 + 7 0,49 + 11 0,17 = 6,72. Dispersion caractérise le degré de dispersion des valeurs d'une variable aléatoire par rapport à sa valeur moyenne et est noté ré(X): ré(X)=M[(SM(X)) 2 ]=M(X 2)
–[M(X)] 2 . Pour une variable aléatoire discrète, la variance a la forme ou il peut être calculé par la formule En substituant les données numériques du problème dans la formule, on obtient : M(X 2)
=
3 2
∙ 0,14+5 2
∙ 0,2+7 2
∙ 0,49+11 2
∙ 0,17 = 50,84 ré(X)
= 50,84-6,72 2
= 5,6816. 4.4.
Deux dés sont lancés deux fois en même temps. Écrire une loi de distribution binomiale pour une variable aléatoire discrète X- le nombre d'occurrences d'un nombre total pair de points sur deux dés. La solution. Introduisons en considération un événement aléatoire MAIS= (sur deux dés en un lancer, un nombre pair de points est tombé au total). En utilisant la définition classique de la probabilité, on trouve R(MAIS)=
où n
- le nombre de résultats possibles du test est trouvé par la règle multiplications : n
= 6∙6 =36, m
-
nombre d'événements favorables MAIS résultats - égaux m= 3∙6=18. Ainsi, la probabilité de succès d'un essai est ρ
=P(MAIS)=
1/2.
Le problème est résolu à l'aide du schéma de test de Bernoulli. Un défi ici consiste à lancer deux dés une fois. Nombre de ces tests n
= 2. Variable aléatoire X prend les valeurs 0, 1, 2 avec probabilités R 2 (0)
= La distribution binomiale souhaitée d'une variable aléatoire X peut être représenté comme une série de distribution : X n ρ
n 4.5
. Il y a quatre pièces standard dans un lot de six pièces. Trois items ont été choisis au hasard. Composer la distribution de probabilité d'une variable aléatoire discrète X- le nombre de pièces standard parmi celles sélectionnées et trouver son espérance mathématique. La solution. Valeurs d'une variable aléatoire X sont les nombres 0,1,2,3. Il est clair que R(X=0)=0, car il n'y a que deux pièces non standard. R(X=1) = R(X= 2) = R(X=3) = Loi de distribution d'une variable aléatoire X représenter sous forme de série de distribution : X n ρ
n Valeur attendue M(X)=1
∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2. 4.6
. Prouver que l'espérance mathématique d'une variable aléatoire discrète X- nombre d'occurrences de l'événement MAIS dans n tests indépendants, dans chacun desquels la probabilité d'occurrence d'un événement est égale à ρ
- est égal au produit du nombre d'essais par la probabilité qu'un événement se produise dans un essai, c'est-à-dire pour prouver que l'espérance mathématique de la distribution binomiale M(X)
=n .
ρ
, tandis que la variance ré(X)
=np
. La solution. Valeur aléatoire X peut prendre les valeurs 0, 1, 2…, n. Probabilité R(X= k) est trouvé par la formule de Bernoulli : R(X=k)= R n(k)= Série de distribution variable aléatoire X ressemble à: X n ρ
n q n où q=
1-
ρ
. Pour l'espérance mathématique, nous avons l'expression : M(X)= Dans le cas d'un test, c'est-à-dire avec n= 1 pour une variable aléatoire X 1 - le nombre d'occurrences de l'événement MAIS- la série de distribution a la forme : X n ρ
n M(X 1)=
0 q +
1
∙ p
=
p ré(X 1)
=
p
–
p 2
=
p(1-
p)
=
pq. Si un X k - le nombre d'occurrences de l'événement MAIS dans quel test, alors R(X à)=
ρ
et X=X 1 +X 2 +….+X n . De là, nous obtenons M(X)=M(X 1
)+M(X 2)+
… +M(X n)=
nρ,
ré(X)=D(X 1)+D(X 2)+
...
+D(X n)=npq. 4.7.
QCD vérifie la normalisation des produits. La probabilité que l'item soit standard est de 0,9. Chaque lot contient 5 articles. Trouver l'espérance mathématique d'une variable aléatoire discrète X- le nombre de lots dont chacun sera égal à 4 produits standards - si 50 lots sont soumis à vérification. La solution. La probabilité qu'il y ait 4 articles standards dans chaque lot sélectionné au hasard est constante ; notons-le par ρ
.Puis l'espérance mathématique de la variable aléatoire Xéquivaut à M(X)=
50∙ρ.
Trouvons la probabilité ρ
selon la formule de Bernoulli : ρ=P 5 (4)= M(X)=
50∙0,32=16. 4.8
. Trois dés sont lancés. Trouvez l'espérance mathématique de la somme des points abandonnés. La solution. Vous pouvez trouver la distribution d'une variable aléatoire X- la somme des points lâchés puis son espérance mathématique. Cependant, cette voie est trop lourde. Il est plus facile d'utiliser une autre astuce, représentant une variable aléatoire X, dont l'espérance mathématique doit être calculée, comme une somme de plusieurs variables aléatoires plus simples, dont l'espérance mathématique est plus facile à calculer. Si la variable aléatoire X je est le nombre de points marqués sur je–ème os ( je= 1, 2, 3), puis la somme des points X exprimée sous la forme X = X 1 +X 2 +X 3 . Pour calculer l'espérance mathématique de la variable aléatoire d'origine, il ne reste plus qu'à utiliser la propriété d'espérance mathématique M(X 1
+X 2 +X 3
)=M(X 1
)+M(X 2)+M(X 3
). Il est évident que R(X je =K)=
1/6, À=
1, 2, 3, 4, 5, 6,
je=
1,
2, 3. Par conséquent, l'espérance mathématique d'une variable aléatoire X je a la forme M(X je)
=
1/6∙1
+ 1/6∙2
+1/6∙3
+ 1/6∙4
+ 1/6∙5
+ 1/6∙6
= 7/2, M(X)
=
3∙7/2 = 10,5.
4.9.
Déterminez l'espérance mathématique du nombre d'appareils qui ont échoué pendant le test, si : a) la probabilité de défaillance de tous les appareils est la même R, et le nombre d'appareils testés est égal à n; b) probabilité de défaillance pour je
–
instrument est égal à p je
,
je=
1,
2, … , n. La solution. Soit la variable aléatoire X est le nombre d'appareils défaillants, alors X = X 1 +X 2 + … + å n ,
X je
=
Il est clair que R(X je =
1)=
R je ,
R(X je =
0)=
1–
R je ,je= 1,
2,
…
,n.m. M(X je)=
1∙R je +
0∙(1-R je)=P je , M(X)=M(X 1)+M(X 2)+ … +M(X n)=P 1 +P 2 + ... + P n .
Dans le cas "a", la probabilité de défaillance de l'appareil est la même, c'est-à-dire R je =p,je= 1,
2, …
,n. M(X)=
np. Cette réponse pourrait être obtenue immédiatement si l'on remarquait que la variable aléatoire X a une distribution binomiale avec des paramètres ( n,
p).
4.10.
Deux dés sont lancés deux fois en même temps. Écrire une loi de distribution binomiale pour une variable aléatoire discrète X - le nombre d'occurrences d'un nombre pair de points sur deux dés. La solution. Laisser MAIS=(perte d'un nombre pair au premier dé), B =(perte d'un nombre pair au second dé). La perte d'un nombre pair sur les deux dés lors d'un même lancer sera exprimée par le produit UN B. Alors R
(UN B)
= R(MAIS)∙R(À)
=
Le résultat du deuxième lancer de deux dés ne dépend pas du premier, donc la formule de Bernoulli est applicable lorsque n
=
2,p = 1/4,
q
=
1– p = 3/4.
Valeur aléatoire X peut prendre les valeurs 0, 1, 2 ,
dont on trouve la probabilité par la formule de Bernoulli : R(X= 0)=P 2
(0)
=
q
2
= 9/16, R(X= 1)=P 2
(1)=C R(X= 2)=P 2
(2)=C Série de distribution variable aléatoire X: 4.11.
Le dispositif se compose d'un grand nombre d'éléments fonctionnant indépendamment avec la même très faible probabilité de défaillance de chaque élément dans le temps. t. Trouver le nombre moyen d'échecs au fil du temps téléments, si la probabilité qu'au moins un élément tombe en panne pendant ce temps est de 0,98. La solution.
Nombre de pannes dans le temps téléments - une variable aléatoire X, qui est distribué selon la loi de Poisson, puisque le nombre d'éléments est grand, les éléments fonctionnent indépendamment et la probabilité de défaillance de chaque élément est faible. Le nombre moyen d'occurrences d'un événement dans n essais égaux M(X)
=
np.
Étant donné que la probabilité d'échec Àéléments de n s'exprime par la formule R n
(À)
où
=
np, alors la probabilité qu'aucun élément ne tombe en panne dans le temps t
nous arrivons à K = 0: R n
(0)= e - . Par conséquent, la probabilité de l'événement opposé est dans le temps t
au moins un élément échoue - égal à 1 -e -
. Selon la condition du problème, cette probabilité est égale à 0,98. De l'équation 1
- e -
= 0,98, e -
= 1 – 0,98 =
0,02, d'ici
=
-ln
0,02
4. Alors pour le moment t fonctionnement de l'appareil échouera en moyenne 4 éléments. 4.12
. Le dé est lancé jusqu'à ce qu'un "deux" soit obtenu. Trouvez le nombre moyen de lancers. La solution. On introduit une variable aléatoire X- le nombre de tests qui doivent être effectués jusqu'à ce que l'événement qui nous intéresse se produise. La probabilité que X= 1 est égal à la probabilité qu'en un coup de dé, un "deux" tombe, c'est-à-dire R(X= 1)
= 1/6. Événement X= 2 signifie que lors du premier essai, les "deux" ne sont pas tombés, mais lors du second, ils sont tombés. Probabilité d'événement X= 2 on trouve par la règle de multiplication des probabilités d'événements indépendants : R(X= 2)
= (5/6)∙(1/6) De même, R(X= 3)
= (5/6) 2 ∙1/6, R(X= 4)
= (5/6) 2 ∙1/6 etc. On obtient une série de distributions de probabilité : (5/6) à
∙1/6 Le nombre moyen de lancers (essais) est l'espérance mathématique M(X)
=
1∙1/6 +
2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6
+ … + À
(5/6) À -1 ∙1/6
+ … = 1/6∙(1+2∙5/6 +3∙(5/6) 2
+ … + À
(5/6) À -1
+ …) Trouvons la somme de la série : Par conséquent, M(X)
=
(1/6) (1/ (1 –
5/6) 2
= 6. Ainsi, il faut effectuer en moyenne 6 lancers de dés jusqu'à ce qu'un "deux" tombe. 4.13.
Des tests indépendants sont effectués avec la même probabilité d'occurrence de l'événement MAISà chaque épreuve. Trouver la probabilité qu'un événement se produise MAIS si la variance du nombre d'occurrences de l'événement dans trois essais indépendants est de 0,63 .
La solution. Le nombre d'occurrences de l'événement dans les trois essais est une variable aléatoire X répartis selon la loi du binôme. La variance du nombre d'occurrences d'un événement dans des essais indépendants (avec la même probabilité d'occurrence d'un événement dans chaque essai) est égale au produit du nombre d'essais par la probabilité d'occurrence et de non-occurrence de l'événement ( tâche 4.6) ré(X)
=
npq.
Par état n
=
3,
ré(X)
=
0,63, vous pouvez donc R trouver à partir de l'équation 0,63
= 3∙R(1-R), qui a deux solutions R 1
=
0,7 et R 2
=
0,3.
1.2.
p4=0,1 ; 0 pour x≤-1,
(fig.5)
https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 pour x≤a,
,
La courbe normale est symétrique par rapport à la droite x=m, a un maximum en x=a égal à .
,
La solution.
La probabilité qu'aucun blason ne tombe : P(0) = 0,5*0,5*0,5= 0,125
P(1) = 0,5
*0,5*0,5 + 0,5*0,5
*0,5 + 0,5*0,5*0,5
= 3*0,125=0,375
P(2) = 0,5
*0,5
*0,5 + 0,5
*0,5*0,5
+ 0,5*0,5
*0,5
= 3*0,125=0,375
La probabilité que trois blasons tombent : P(3) = 0,5 * 0,5 * 0,5 = 0,125
Vérifier : P = P(0) + P(1) + P(2) + P(3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 X 0
1
2
3
P 0,125
0,375
0,375
0,125
La solution.
Considérez l'événement A - un coup sur la cible. Les occurrences possibles de cet événement sont les suivantes :
Alors la probabilité de l'événement A - exactement un coup sur la cible, sera égale à : P(A) = 0,12+0,17+0,68 = 0,97 
, avec laquelle la variable aléatoire prend chacune des valeurs, c'est-à-dire 
.Sens
...
Probabilité
...
sont incompatibles et les seuls possibles : ils forment un système complet d'événements. Par conséquent, la somme de leurs probabilités est égale à un :
.Montant gagnant -100
900
2900
Probabilité 0,94
0,04
0,02
Fonction de distribution d'une variable aléatoire discrète : construction
, qui détermine la probabilité que la valeur de la variable aléatoire X inférieur ou égal à la valeur limite X.Sens 1
2
3
4
5
6
Probabilité 1/6
1/6
1/6
1/6
1/6
1/6
Sens 0
1
2
3
Probabilité 1/30
3/10
1/2
1/6
. À
Fonction de distribution d'une variable aléatoire discrète : calcul
Durée du mariage (années) Numéro Probabilité F(X)
0
10
0,002
0,002
1
80
0,013
0,015
2
177
0,029
0,044
3
209
0,035
0,079
4
307
0,051
0,130
5
335
0,056
0,186
6
358
0,060
0,246
7
413
0,069
0,314
8
432
0,072
0,386
9
402
0,067
0,453
10 ou plus 3287
0,547
1,000
Total 6010
1
Relation entre la loi de distribution d'une variable aléatoire discrète et l'espérance mathématique et la variance
(1)
, (2)
.
,
ANNEXE
Éléments de combinatoire
Actions sur les événements
;
;
La définition classique de la probabilité
, favorable à la survenance de l'événement MAIS, au nombre total d'expériences 
:
Formule de multiplication de probabilité
peut être trouvé à l'aide de la formule :
- probabilité d'événement MAIS,
- probabilité d'événement À,
- probabilité d'événement Àà condition que l'événement MAIS déjà arrivé.
Formule d'addition de probabilité
peut être trouvé à l'aide de la formule :
- probabilité d'occurrence conjointe d'événements MAIS et À.
Formule de probabilité totale
,
,
…,
Appelons-les des hypothèses. Également connu 
- probabilité de réalisation je-ième hypothèse et 
- la probabilité d'occurrence de l'événement A lors de l'exécution jeème hypothèse. Alors la probabilité de l'événement MAIS peut être trouvé à l'aide de la formule :
Schéma de Bernoulli
dans le schéma de Bernoulli, c'est le nombre d'occurrences d'un événement, qui correspond à la probabilité la plus élevée. Peut être trouvé en utilisant la formule:
Variables aléatoires
Caractéristiques numériques des variables aléatoires discrètes
X
R
fonction de répartition
Questions pour l'examen
.
.
,
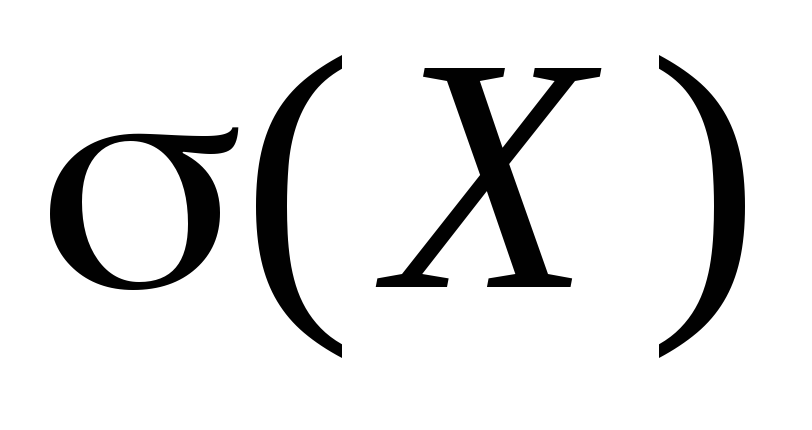0,3(0,7) 2
= 0,441,
(0,3) 2 0,7
= 0,189,
.
.
.
,
,R 2 (1)
=
∙
,R 2 (2)
=
=1/5,
= 3/5,
= 1/5.
ρ
à
(1-ρ
) n-à
ρq n- 1
ρq n- 2
ρ
n
ρq n -
1
+2
ρ
2
q n -
2
+…+.n
ρ
n
= 0,94∙0,1=0,32.
.
,R∙q
=
6/16,
,
R 2
=
1/16.
,
Àg
À -1
= (
g À)
g
.
