වෙනස සමීකරණ උදාහරණය. නියත සංගුණක සමඟ සාමාන්ය රේඛීය වෙනස්කම් සමීකරණ විසඳුම. ස්වයංක්‍රීය පාලන පද්ධතිවල අවකල සමීකරණ. ස්වයංක්‍රීය පාලන පද්ධතිවල අවකල සමීකරණ සම්පාදනය කිරීමේ ක්‍රමවේදය

සමීකරණ භාවිතය අපගේ ජීවිතයේ බහුලව දක්නට ලැබේ. ඒවා බොහෝ ගණනය කිරීම්, ව්යුහයන් තැනීම සහ ක්රීඩා වල පවා භාවිතා වේ. අතීතයේ සිටම මිනිසා විසින් සමීකරණ භාවිතා කර ඇති අතර එතැන් සිට ඒවායේ භාවිතය වැඩි වී ඇත. වෙනස සමීකරණයක් යනු කිසියම් අවස්ථාවක දී යම් නොදන්නා ශ්‍රිතයක අගයක් ලබා දී ඇති එකකින් වෙන් කරන ලද ලක්ෂ්‍ය එකක හෝ වැඩි ගණනක අගය සමඟ සම්බන්ධ කරන සමීකරණයකි. උදාහරණයක්:

\[Г (z+1) = zГ(z)\]

නියත සංගුණක සහිත වෙනස්කම් සමීකරණ සඳහා, සංවෘත ආකාරයෙන් විසඳුම් සෙවීම සඳහා සවිස්තරාත්මක ක්රම තිබේ. n වන අනුපිළිවෙලෙහි සමජාතීය සහ සමජාතීය වෙනස්කම් සමීකරණ පිළිවෙලින් සමීකරණ මගින් ලබා දෙනු ලැබේ, එහිදී \ නියත සංගුණක වේ.

සමජාතීය වෙනස්කම් සමීකරණ.

n වන අනුපිළිවෙල සමීකරණය සලකා බලන්න

\[(a_nE^n + a(n-1)E^n1 + \cdots +a_1E + a_1)y(k) = 0 \]

යෝජිත විසඳුම පහත ආකාරයෙන් සෙවිය යුතුය:

එහිදී \ යනු නිශ්චය කළ යුතු නියතය වේ. සමීකරණය මගින් ලබා දෙන යෝජිත විසඳුමේ වර්ගය වඩාත් පොදු නොවේ. අවසර ලත් අගයන් \[ e^r.\] හි බහුපදයේ මූලයන් ලෙස ක්‍රියා කරයි \[ \beta = e^r \] සමඟින් යෝජිත විසඳුම වන්නේ:

එහිදී \[\beta\] නිශ්චය කළ යුතු නියතය වේ. සමීකරණය ආදේශ කිරීම සහ \ සැලකිල්ලට ගනිමින්, අපි පහත ලක්ෂණ සමීකරණය ලබා ගනිමු:

සමජාතීය වෙනස්කම් සමීකරණ. අවිනිශ්චිත සංගුණක ක්රමය. n වන අනුපිළිවෙලෙහි වෙනස සමීකරණය සලකා බලන්න

\[ (a_nEn +a_(n-1)En^-1+\cdots+ a_1E +a_1)y(k) =F(k) \]

ප්රතිචාරය මේ වගේ ය:

මට මාර්ගගතව වෙනස සමීකරණය විසඳිය හැක්කේ කොතැනින්ද?

ඔබට අපගේ වෙබ් අඩවිය https: // අඩවියේ සමීකරණය විසඳා ගත හැකිය. නොමිලේ මාර්ගගත විසදුම්කරු තත්පර කිහිපයකින් ඕනෑම සංකීර්ණතාවයක සබැඳි සමීකරණයක් විසඳීමට ඔබට ඉඩ සලසයි. ඔබ කළ යුතුව ඇත්තේ ඔබේ දත්ත විසඳුමට ඇතුළු කිරීම පමණි. ඔබට වීඩියෝ උපදෙස් නැරඹිය හැකි අතර අපගේ වෙබ් අඩවියේ සමීකරණය විසඳන්නේ කෙසේදැයි ඉගෙන ගත හැකිය. ඔබට කිසියම් ප්‍රශ්නයක් ඇත්නම්, ඔබට ඒවා අපගේ Vkontakte කණ්ඩායම http://vk.com/pocketteacher වෙතින් ඇසිය හැකිය. අපගේ කණ්ඩායමට සම්බන්ධ වන්න, ඔබට උදව් කිරීමට අපි සැමවිටම සතුටු වන්නෙමු.

ප්‍රායෝගිකව, සරලම වෙනස්කම් සමීකරණ පැන නගින්නේ, උදාහරණයක් ලෙස, බැංකු තැන්පතුවක වටිනාකම අධ්‍යයනය කිරීමේදී ය. මෙම අගය Y x විචල්‍යයකි, එය තර්කයේ පූර්ණ සංඛ්‍යා අගයන් සමඟ ස්ථාපිත නීතියට අනුව එකතු වන එකතුව නියෝජනය කරයි. x. වසරකට රුපියල් 100 ක සංයුක්ත පොලී උපචිතයට යටත්ව Y o මුදල බැංකුවේ තැන්පත් කිරීමට ඉඩ දෙන්න. වසරකට වරක් පොලී ගණනය කිරීමට ඉඩ දෙන්න xතැන්පත් කර ඇති වසර ගණන දක්වයි (x = 0, 1, 2,...). කල් ඉකුත් වූ පසු දායක මුදලේ වටිනාකම සඳහන් කරමු xවසර ගණනාවකට පසු Y x . අපිට ලැබෙනවා

Y x= (1+r)Y x-1.

ආරම්භක එකතුව Y o නම්, x = 0 හි Y x = Y o ආරම්භක කොන්දේසියට යටත්ව ප්‍රතිඵලයක් ලෙස ලැබෙන වෙනස්කම් සමීකරණයට විසඳුමක් සෙවීමේ ගැටලුවට අපි පැමිණෙමු. ප්‍රතිඵලයක් ලෙස ලැබෙන වෙනස සමීකරණයේ Y x සහ මෙම විචල්‍යයේ අගය අඩංගු වේ. වසරකට පෙර, i.e. Yx-1; මෙම නඩුවේ තර්කය xවෙනස සමීකරණයේ පැහැදිලිව ඇතුළත් නොවේ.

පොදුවේ ගත් කල, සාමාන්ය වෙනස්කම් සමීකරණයශ්‍රේණිය සඳහා සලකා බලන Y = Y(x) ශ්‍රිතයේ අගයන් අතර සම්බන්ධතාවයක් ඇති කරයි සමාන පරතරයකින් යුත් තර්ක අගයන් x, නමුත් සාමාන්‍ය භාවය නැතිවීමකින් තොරව අපට උපකල්පනය කළ හැකිය අපේක්ෂිත ශ්‍රිතය එකකට සමාන පියවරක් සහිත තර්කයේ සමාන දුර අගයන් සඳහා අර්ථ දක්වා ඇත. මේ අනුව, තර්කයේ ආරම්භක අගය නම් x, එවිට එහි සමාන දුර අගයන් මාලාව x , x+1, x+2,... සහ ප්‍රතිවිරුද්ධ දිශාවට වනු ඇත: x , x-1, x-2,.... අනුරූප අගයන් ශ්‍රිතයේ Y x, Y x+ 1, Y x+2, ... හෝ Y x , Y x-1, Y x-2, .... ඊනියා අර්ථ දක්වන්න වෙනස්කම්පහත සූත්‍ර භාවිතා කරමින් Y x ශ්‍රිතයේ විවිධ ඇණවුම්:

පළමු අනුපිළිවෙලෙහි වෙනස්කම්

ඩී Y x = Y x+1 - Y x ,

D Y x+1 =Y x+2 - Y x+1,

D Y x+2 = Y x+3 - Y x+2,

... ... ... ... ...

දෙවන අනුපිළිවෙලෙහි වෙනස්කම්

D 2 Y x = D Y x+1 - D Y x,

D 2 Y x+1 = D Y x+2 - D Y x+1 ,

D 2 Y x+2 = D Y x+3 - D Y x+2 ,

... ... ... ... ...

තුන්වන අනුපිළිවෙලෙහි වෙනස්කම්

D 3 Y x \u003d D 2 Y x + 1 - D 2 Y x,

D 3 Y x+1 = D 2 Y x+2 - D 2 Y x+1 ,

... ... ... ... ...

සාමාන්‍ය වෙනස සමීකරණය එක් ස්වාධීන තර්කයක අගයන් සම්බන්ධ සමීකරණයක් ලෙස හැඳින්වේ x, එහි කාර්යයන් Y xසහ මෙම කාර්යයේ විවිධ ඇණවුම්වල වෙනස්කම්ඩී Y x, D 2 Yx, D 3 Y x, .... එවැනි සමීකරණයක් පහත පරිදි සාමාන්‍ය ආකාරයෙන් ලිවිය හැකිය:

j ( x, Y x,ඩී Y x, D 2 Y x D 3 Y x, D n Y x ) = 0, (10.1)

කුමනස්වරූපයෙන් අවකල සමීකරණයකට සමාන වේ.

නියෝගවෙනස සමීකරණය මෙම සමීකරණයේ ඇතුළත් ඉහළම වෙනස අනුපිළිවෙල ලෙස හැඳින්වේ. වෙනස සමීකරණය (10.1) බොහෝ විට ලිවීමට වඩාත් පහසු වන්නේ නොදන්නා ශ්‍රිතයේ වෙනස්කම් නොව, තර්කයේ අනුක්‍රමික අගයන් සඳහා එහි අගයන්, එනම් ප්‍රකාශ කිරීමටඩී Y x, D 2 Y x, D 3 Y x ,... හරහා Y x , Yx+1 , Y x+2, .... සමීකරණය (10.1) ආකාර දෙකෙන් එකකට අඩු කළ හැක:

y ( x , Y x , Y x+1, ...,Y x+n ) = 0, (10.2)

x ( x , Y x , Y x-1, ..., Y x -n) = 0.(10.3)

සාමාන්‍ය වෙනස සමීකරණයේ සාමාන්‍ය විවික්ත විසඳුම Y x n th අනුපිළිවෙල හරියටම අඩංගු x (x = 0, 1. 2,...) ශ්‍රිතයක් නියෝජනය කරයි nඅත්තනෝමතික නියතයන්:

Y x= Y(x, C 1, C 2 ,..., C n ).

ස්පයිඩර් ආකෘතිය

ඕනෑම නිශ්චිත නිෂ්පාදනයක වෙළඳපල පහත සඳහන් සැපයුම් සහ ඉල්ලුම් කාර්යයන් මගින් සංලක්ෂිත කිරීමට ඉඩ දෙන්න:

D= D(P), S = S(P).

සමතුලිතතාවය පැවතීමට නම්, වෙළඳපොලේ ඇති භාණ්ඩ විකුණා අවසන් වන පරිදි මිල විය යුතුය

D( P) = S(P).

සමතුලිත මිල මෙම සමීකරණය මගින් ලබා දී ඇත (එයට බොහෝ විසඳුම් තිබිය හැක), සහ අනුරූප මිලදී ගැනීම් සහ විකුණුම් පරිමාව,, - පහත සමීකරණය මගින්:

D() = S().

සැපයුමේ හෝ ඉල්ලුමේ ප්‍රමාදයක් ඇති විට ගතික ආකෘතියක් ලබා ගනී. විවික්ත විශ්ලේෂණයේ සරලම ආකෘතියට නියත ප්‍රමාදයක් හෝ එක් පරතරයක සැපයුම් ප්‍රමාදයක් ඇතුළත් වේ:

Dt= D (P t) සහ S t = S (P t-1).

ප්‍රශ්නගත භාණ්ඩ නිෂ්පාදනය සඳහා පරතරය සඳහා තෝරාගත් නිශ්චිත කාලයක් අවශ්‍ය නම් මෙය සිදු විය හැක. ආකෘතියේ ක්‍රියාකාරිත්වය පහත පරිදි වේ: පෙර කාල පරිච්ඡේදයේ ලබා දී ඇති P t-1 සඳහා, වත්මන් කාල සීමාව තුළ වෙළඳපොලේ සැපයුම් පරිමාව S (P t-1) වන අතර P t හි අගය විය යුතුය. ඉදිරිපත් කරන ලද භාණ්ඩවල සම්පූර්ණ පරිමාව මිලදී ගන්නා ලෙස සකසන්න. වෙනත් වචන වලින් කිවහොත්, P t සහ මිලදී ගැනීම් සහ විකුණුම් පරිමාව X t සමීකරණය මගින් සංලක්ෂිත වේ:

X ටී= D (P t) = S (P t-1).

එබැවින්, ආරම්භක මිල P o දැන ගැනීමෙන්, මෙම සමීකරණවල උපකාරයෙන් අපට P 1 සහ X 1 හි අගයන් ලබා ගත හැකිය. පසුව, පවතින මිල P 1 භාවිතා කර, අනුරූප සමීකරණ වලින් අපි P හි අගයන් ලබා ගනිමු. 2 සහ X 2, සහ එසේ ය. සාමාන්‍යයෙන්, P t හි වෙනස පළමු අනුපිළිවෙලෙහි වෙනස සමීකරණයකින් සංලක්ෂිත වේ ( තනි-විරාමයපසුබැසීම):

D (P t) = S (P t-1).

රූපය 5 හි පෙන්වා ඇති රූප සටහන මගින් විසඳුම නිදර්ශනය කළ හැක, D සහ S යනු පිළිවෙළින් සැපයුම් සහ ඉල්ලුම් වක්‍ර වේ, සහ සමතුලිත පිහිටීම (අගය සහිත වේ.හා ) ඔවුන්ගේ ඡේදනය වන ස්ථානයට අනුරූප වේ Q. ආරම්භක මොහොතේ මිල P o ට සමාන වේ. S වක්‍රයේ ඇති අනුරූප ලක්ෂ්‍යය Q o 1 කාල පරිච්ෙඡ්දය තුළ සැපයූ ප්‍රමාණය ලබා දෙයි. මෙම සපයන ලද සියලුම ප්‍රමාණය, Q o ට සමාන ඕඩිනේට් (X 1) D වක්‍රයේ Q 1 ලක්ෂ්‍යයෙන් ලබා දී ඇති P 1 මිලට මිල දී ගනු ලැබේ. . දෙවන කාල පරිච්ෙඡ්දය තුළ, චලනය මුලින්ම සිදු වන්නේ Q 1 ලක්ෂ්‍යයේ සිට S වක්‍රයේ ලක්ෂ්‍යය දක්වා සිරස් අතට X 2 ලබා දෙන අතර පසුව තිරස් අතට D වක්‍රයේ Q 2 ලක්ෂ්‍යයට ය. අවසාන ලක්ෂ්‍යය P 2 සංලක්ෂිත වේ. මෙම ක්රියාවලිය දිගටම කරගෙන යාම ලබා දෙයි වෙබ් වගුව fig හි පෙන්වා ඇත. 5. අනුප්‍රාප්තික කාල පරිච්ඡේදවල මිල සහ පරිමාවන් (මිලදී ගැනීම් - විකුණුම්) පිළිවෙළින්, ලකුණුවල ඛණ්ඩාංක වේ Q 1 , Q 2 , Q 3 , ... ඉල්ලුම වක්‍රය මත D. සලකා බලනු ලබන අවස්ථාවක, අනුපිළිවෙල ලක්ෂ්‍ය Q වෙත නැඹුරු වේ. මෙම අවස්ථාවෙහිදී, ලක්ෂ්‍ය Q හි වම් සහ දකුණු පැතිවල විකල්ප වශයෙන් ස්ථානගත වේ. ඒ අනුව, P t හි අගයන් නැඹුරු වේ, දෙපස විකල්පව පිහිටා ඇත. මිලදී ගැනීම් පරිමාවන් සමඟ තත්වය හරියටම සමාන වේ - විකුණුම් (X t ).

රේඛීය සැපයුම සහ ඉල්ලුම ශ්‍රිත සඳහා විසඳුම වීජීය වශයෙන් ලබා ගත හැක: D = a + aP, S = b+ bP සමතුලිතතා අගයන්හා සමීකරණ මගින් ලබා දෙනු ඇත

A + a = b + b ,

එනම්

= (අ - b) / (b - a), \u003d (b a - a b) / (b - a). (10.4) p t-1. (10.7)

සමීකරණ (10.7) සමාන වේ (10.5), ඒවා සමතුලිතතා මට්ටම් වලින් බැහැරවීම් විස්තර කරනවා හැර (ඒවා පවතින බව දැන් දන්නා කරුණකි). මෙම සමීකරණ දෙකම පළමු අනුපිළිවෙලෙහි වෙනස්කම් සමීකරණ වේ. අපි c = b /a දමා එය සමීකරණයට (10.7) ආදේශ කරමු, එවිට වෙනස සමීකරණය සම්බන්ධයෙන් ආර් ටීවනු ඇත

ආර් ටී = c p t-1 . (10.8)

මෙම අගය සඳහා ආර් o මේ මොහොතේ t = 0 (10.8) සිට අපි විසඳුම ලබා ගනිමු:

ආර් t = ආර් o c t,

හෝ

P t = + (P o - ) c t .

සාමාන්ය රේඛීය වෙනස්කම් සමීකරණ විසඳුම

නියත සංගුණක සමඟ

රේඛීය විවික්ත පද්ධතියක ප්‍රතිදානය සහ ආදානය අතර සම්බන්ධය නියත සංගුණක සහිත සාමාන්‍ය රේඛීය වෙනස සමීකරණයකින් විස්තර කළ හැක.

,

කොහෙද y[n]- මේ මොහොතේ ප්රතිදාන සංඥාව n,

x[n]- මේ මොහොතේ ආදාන සංඥාව n,

a i,ආ කේනියත සංගුණක වේ.

එවැනි සමීකරණ විසඳීමට ක්රම දෙකක් භාවිතා කළ හැකිය.

• සෘජු ක්රමය,
• ක්රමය Z - පරිවර්තනයන්.

අපි මුලින්ම සෘජු ක්‍රමය භාවිතා කරමින් රේඛීය වෙනස සමීකරණයක විසඳුම සලකා බලමු.

සමජාතීය (ශුන්‍ය නොවන දකුණු පස සහිත) රේඛීය වෙනස සමීකරණයක සාමාන්‍ය විසඳුම o එකතුවට සමාන වේ සාමාන්ය විසඳුමරේඛීය සමජාතීය වෙනස සමීකරණය සහ පෞද්ගලික තීරණයසමජාතීය සමීකරණය

සමජාතීය වෙනස සමීකරණයේ පොදු විසඳුම ( ශුන්ය-ආදානයප්රතිචාරය) y h [n]

ලෙස අර්ථ දක්වා ඇත

.

මෙම විසඳුම සමජාතීය සමීකරණයට ආදේශ කිරීම, අපි ලබා ගනිමු

එවැනි බහුපදයක් ලෙස හැඳින්වේ ලක්ෂණ බහුපදපද්ධති. ඔහුට තිබේ එන්මුල් . මූලයන් සැබෑ හෝ සංකීර්ණ විය හැකි අතර සමහර මූලයන් සමපාත විය හැක (බහු).

මුල් නම් සැබෑ සහ වෙනස් වේ, එවිට සමජාතීය සමීකරණයේ විසඳුමේ ස්වරූපය ඇත

එහිදී සංගුණක

යම් මූලයක් නම්, උදාහරණයක් ලෙස, λ1බහුත්වයක් ඇත එම්, එවිට විසඳුමේ අනුරූප පදය ස්වරූපය ගනී

සමජාතීය සමීකරණයේ සියලුම සංගුණක සහ, පිළිවෙළින්, ලාක්ෂණික බහුපදයේ සැබෑ නම්, සරල සංකීර්ණ සංයුජ මූලයන්ට අනුරූප වන විසඳුමේ පද දෙක සංගුණක වන අතර, ආකෘතියෙන් (ලිඛිත) නිරූපණය කළ හැක ඒ,බීආරම්භක කොන්දේසි අනුව තීරණය වේ.

පුද්ගලික විසඳුම් වර්ගය y p [n]සමීකරණය දකුණු පැත්තේ (ආදාන සංඥාව) මත රඳා පවතින අතර පහත වගුව අනුව තීරණය වේ

වගුව 1. දකුණු පැත්තේ විවිධ අක්ෂර සඳහා විශේෂිත විසඳුම් වර්ගය

ආදාන සංඥාවx[n]	පෞද්ගලික තීරණයyp[n]
ඒ(නිරන්තර)

Z-පරිවර්තන ක්රමය මගින් රේඛීය වෙනස සමීකරණයේ විසඳුම යෙදීමෙන් සමන්විත වේ Z- රේඛීයත්වය සහ කාල මාරුව යන ගුණාංග භාවිතා කරමින් සමීකරණයට පරිවර්තනය කිරීම. එහි ප්‍රතිඵලය වන්නේ රේඛීය වීජීය සමීකරණයකි Z- අපේක්ෂිත කාර්යයේ රූප. ආපසු හැරවීම Z- පරිවර්තනය කාල වසම තුළ අපේක්ෂිත විසඳුම ලබා දෙයි. ප්‍රතිලෝම Z-පරිවර්තනය ලබා ගැනීම සඳහා, තාර්කික ප්‍රකාශනයක් සරල (මූලික) භාග බවට වියෝජනය කිරීම බොහෝ විට භාවිතා වේ, මන්ද වෙනම මූලික භාගයකින් ප්‍රතිලෝම පරිවර්තනය සරල ස්වරූපයක් ඇති බැවිනි.

ප්‍රතිලෝම Z-පරිවර්තනය ගණනය කිරීම සඳහා වෙනත් ක්‍රම කාල වසම වෙත ගෙන යාමට ද භාවිතා කළ හැකි බව සලකන්න.

උදාහරණයක්. රේඛීය වෙනස සමීකරණය මගින් විස්තර කර ඇති පද්ධතියේ ප්‍රතිචාරය (ප්‍රතිදාන සංඥාව) ආදාන සංඥාවට තීරණය කරමු.

විසඳුමක්.

1. සමීකරණය විසඳීම සඳහා සෘජු ක්රමය.

සමජාතීය සමීකරණය. එහි ලාක්ෂණික බහුපද වේ.

බහුපද මූලයන් .

සමජාතීය සමීකරණයක විසඳුම.

එතැන් සිට, අපි ආකෘතියේ විශේෂිත විසඳුමක් නිර්වචනය කරමු .

එය සමීකරණයට ආදේශ කරන්න

නියතයක් සොයා ගැනීමට වෙතපිළිගන්නවා n=2. ඉන්පසු

හෝ, K=2.33

එබැවින් විශේෂිත විසඳුම සහ වෙනස සමීකරණයේ පොදු විසඳුම (1)

අපි නියතයන් සොයා ගනිමු 1 සිටහා 2 සිට. මේ සඳහා අපි සකස් කරමු n=0, පසුව මුල් වෙනස සමීකරණයෙන් අපි ලබා ගනිමු . මෙම සමීකරණය සඳහා

ඒක තමයි . ප්‍රකාශනයෙන් (1)

ප්රතිඵලයක් වශයෙන්,

.

සඳහා (1) ප්‍රකාශනයෙන් n=1අපිට තියනවා .
අපි C 1 සහ C 2 සඳහා පහත සමීකරණ දෙක ලබා ගනිමු

.

මෙම පද්ධතියේ විසඳුම පහත අගයන් ලබා දෙයි: C 1 =0.486 සහ C 2 = -0.816.

එබැවින්, මෙම සමීකරණයේ පොදු විසඳුම

2. Z-පරිවර්තන ක්රමය මගින් විසඳුම.

Z ගන්න - මුල් වෙනස සමීකරණයෙන් පරිවර්තනය , කාල මාරුවේ දේපල (ප්රමේයය) සැලකිල්ලට ගනිමින් 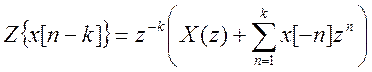. අපිට ලැබෙනවා

පරීක්ෂණ ප්රශ්න:

1. ජාල ශ්‍රිතය යනු කුමක්ද?

2. වෙනස සමීකරණයක් ලෙස හඳුන්වන සමීකරණය කුමක්ද?

3. 1 වන අනුපිළිවෙලෙහි වෙනස්කම් සමීකරණ ලෙස හඳුන්වන සමීකරණ මොනවාද?

4. 1 වන අනුපිළිවෙලෙහි සමජාතීය වෙනස්කම් සමීකරණයේ පොදු විසඳුම සොයා ගන්නේ කෙසේද?

5. මූලික ලෙස හඳුන්වන වෙනස සමීකරණයේ විසඳුම කුමක්ද?

6. නියත සංගුණක සහිත සමජාතීය සමීකරණයක පොදු විසඳුම ජ්යාමිතික ප්රගතියක් ලෙස පෙනෙන්නේ ඇයි?

කාර්යයන්.

1. ආරම්භක කොන්දේසිය සමඟ පළමු අනුපිළිවෙලෙහි වෙනස්කම් සමීකරණයක් විසඳීම සඳහා ක්රියා පටිපාටියක් ලියන්න.

2. දී ඇති සමීකරණයක් සඳහා, විශ්ලේෂණාත්මකව පොදු සහ විශේෂිත විසඳුම් සොයන්න.

3. විශ්ලේෂණාත්මක විසඳුම සමඟ පුනරාවර්තන සූත්රය මගින් ගණනය කිරීම්වල ප්රතිඵල සසඳන්න.

4. ආරම්භක තත්වයේ කැළඹීම, සමීකරණයේ සංගුණක, දකුණු පැත්තේ ප්රතිඵලය බලපාන ආකාරය සොයා බලන්න.

				දිශාවන්

1 වන අනුපිළිවෙලෙහි වෙනස සමීකරණයේ පොදු විසඳුම අපි සොයා ගනිමු

. (1)

පුනරාවර්තන සූත්‍රය භාවිතා කිරීම සඳහා අපි සමජාතීය සමීකරණයේ විශේෂිත විසඳුමක් ලබා ගනිමු: . ජාලකයේ සෑම ඊළඟ නෝඩයකම Y හි අගය දෙගුණ වන බැවින්, අපට q=2 යන හරය සමඟ ජ්‍යාමිතික ප්‍රගතියක් ලැබේ:

සමජාතීය සමීකරණයේ විශේෂිත විසඳුමක් අපි ස්වරූපයෙන් සොයා ගනිමු: , A යනු අවිනිශ්චිත සංගුණකයකි. එවිට , , සහ, ලබා ගත් අගය ලබා දී ඇති දකුණු පැත්තට සමාන කරමින්, අපි අවිනිශ්චිත සංගුණකය A= සොයා ගනිමු. අවසාන වශයෙන්, පොදු විසඳුම: .

ආරම්භක කොන්දේසිය භාවිතා කරමින්, අපි නියතය සොයා ගනිමු: . අවසාන වශයෙන්, දී ඇති මූලික කොන්දේසියක් සඳහා විශේෂිත විසඳුමක්:

.

විසඳුමේ කැළඹීම සහ ආරම්භක තත්වය සඳහා විසඳුමේ ස්ථායීතාවය අධ්යයනය කිරීම සඳහා පහත සමීකරණය සලකා බලන්න:

අවුල් සහගත ආරම්භක තත්ත්වය සමඟ

(මෙන්න කැළඹීමේ විශාලත්වය). මුල් සමීකරණය (1) අඩු කිරීමෙන්, අපි කැළඹීම සඳහා වෙනස සමීකරණය ලබා ගනිමු:

ආරම්භක තත්ත්වය සමඟ. මෙම සමීකරණයට විසඳුම වන්නේ: , i.e. ඕනෑම නෝඩයක කුඩා කැළඹීමක් පවා වැඩි වන නෝඩය සමඟ ඝාතීය ලෙස වර්ධනය වේ.

ප්‍රත්‍යාවර්තී සූත්‍රය වෙනස් කිරීම මගින් සමීකරණයේ ආරම්භක තත්ත්වය, දකුණු පස සහ සංගුණකවල කැළඹීම්වල බලපෑම විමර්ශනය කිරීම සඳහා ශිෂ්‍යයා ඉහත විස්තර කළ යුතුය.

සඟරාවේ ලැයිස්තුවේ සිටින ශිෂ්‍ය සංඛ්‍යාවට අනුව විකල්පය C ++ ක්‍රමලේඛන භාෂාවෙන් විසඳිය යුතුය (බිල්ඩර් පරිසරය භාවිතා කිරීමට අවසර ඇත) හෝ පැස්කල් (ඩෙල්ෆි පරිසරය භාවිතා කිරීමට අවසර ඇත) .

1. සංඛ්යාත්මක විසඳුමක් ලබා ගැනීම සඳහා පුනරාවර්තන සූත්රය.
2. වෙනස සමීකරණයේ විශ්ලේෂණාත්මක විසඳුම. සාමාන්‍ය විසඳුම සහ ලබා දී ඇති මූලික කොන්දේසි සපුරාලන විශේෂිත විසඳුමක්.
3. ආරම්භක තත්වයේ කැළඹීමක් සඳහා විසඳුමේ ස්ථායීතාවය සහ විසඳුම විශ්ලේෂණාත්මකව විමර්ශනය කරන්න.

b) සමීකරණයේ සංගුණක කැළඹී ඇති විට;

ඇ) දකුණු පැත්ත කැළඹී ඇති විට.

මාතෘකාව: 2 වන අනුපිළිවෙලෙහි වෙනස සමීකරණ

පරීක්ෂණ ප්රශ්න:

1. 2 වන අනුපිළිවෙල වෙනස් සමීකරණ ලෙස හඳුන්වන සමීකරණ මොනවාද?

2. ලක්ෂණ සමීකරණයක් යනු කුමක්ද?

3. ලාක්ෂණික සමීකරණයේ සැබෑ මූලයන් සමඟ සමජාතීය 2 වන අනුපිළිවෙල වෙනස් සමීකරණයක විශේෂිත විසඳුමක් පෙනෙන්නේ කෙසේද?

4. ලාක්ෂණික සමීකරණයේ සංකීර්ණ මූලයන් සහිත සමජාතීය 2 වන අනුපිළිවෙල වෙනස් සමීකරණයක විශේෂිත විසඳුමක් පෙනෙන්නේ කෙසේද?

5. 2 වන අනුපිළිවෙලෙහි සමජාතීය වෙනස්කම් සමීකරණයේ පොදු විසඳුම සොයා ගන්නේ කෙසේද?

6. 2 වන අනුපිළිවෙලෙහි වෙනස සමීකරණයේ සංඛ්‍යාත්මක සහ විශ්ලේෂණාත්මක විසඳුම කුමක්ද?

7. හොඳින් කන්ඩිෂන් ලෙස හඳුන්වන කාර්යයන් මොනවාද?

කාර්යයන්

1. මායිම් කොන්දේසි සහිත දෙවන අනුපිළිවෙල සමීකරණයක් සඳහා වෙනස මායිම් අගය ගැටළුවක් විසඳීම සඳහා ක්‍රියා පටිපාටියක් ලියන්න , .

2. දී ඇති සමීකරණයක් සඳහා, විශ්ලේෂණාත්මකව සාමාන්‍ය සහ විශේෂිත විසඳුමක් සොයාගෙන කොන්දේසි නිර්ණායකය පරීක්ෂා කරන්න.

3. විශ්ලේෂණාත්මක විසඳුම සමඟ පුනරාවර්තන සූත්රය මගින් ගණනය කිරීම්වල ප්රතිඵල සසඳන්න.

4. මායිම් තත්වයන් සහ දකුණු පැත්තේ කැළඹීම ප්රතිඵලය බලපාන්නේ කෙසේදැයි සොයා බලන්න.

						2 වන අනුපිළිවෙලෙහි වෙනස සමීකරණයේ සාමාන්‍ය විසඳුම අත්තනෝමතික නියතයන් තෝරා ගැනීමෙන් සොයාගත හැකිය. Cauchy ගැටළු සමඟ, දෙවන අනුපිළිවෙල සමීකරණ සඳහා ලක්ෂ්‍ය දෙකක මායිම්-අගය ගැටළු ද සලකා බලනු ලැබේ, ජාල ශ්‍රිතයේ අගයන් පේළියක නොව, සමහර පරිමිත වල කෙළවරේ පිහිටා ඇති නෝඩ් දෙකකින් ලබා දී ඇත. කොටස: (දේශසීමා කොන්දේසි ) එවැනි ගැටලුවකට විශ්ලේෂණාත්මක විසඳුමක් පොදු විසඳුමේ අත්තනෝමතික නියතයන් සුදුසු තේරීමක් මගින් ලබා ගත හැක. කෙසේ වෙතත්, ආරම්භක කොන්දේසි සමඟ ඇති ගැටළුව මෙන් නොව, මායිම් අගය ගැටළුව අනිවාර්යයෙන්ම අද්විතීය ලෙස විසඳිය නොහැක. එබැවින්, දකුණු පස සහ මායිම් තත්වයන්හි කැළඹීම් (වටකුරු දෝෂ හේතුවෙන්) සඳහා අද්විතීය විසදුම් සහ අඩු සංවේදීතාවයක් ඇති මායිම් අගය ගැටළු පන්තිය පැහැදිලි කිරීම ඉතා වැදගත් වේ. අපි එවැනි කාර්යයන් ලෙස හඳුන්වනු ඇත හොඳින් කොන්දේසි සහිත කොන්දේසි විරහිත මායිම් අගය ගැටලුවක උදාහරණයක් සලකා බලන්න ගැටලුව සකස් කිරීම. ආරම්භක වෙනස සමීකරණය සහ මායිම් කොන්දේසි. සංඛ්යාත්මක විසඳුමක් ලබා ගැනීම සඳහා ක්රියා පටිපාටිය. වෙනස මායිම් අගය ගැටලුවක විශ්ලේෂණාත්මක විසඳුම. පොදු විසඳුම සහ ලබා දී ඇති මායිම් කොන්දේසි තෘප්තිමත් කරන විශේෂිත විසඳුමක්. කොන්දේසි නිර්ණායකය පරීක්ෂා කිරීම. සංඛ්‍යාත්මක විසඳුමේ සහ විශ්ලේෂණාත්මක විසඳුමේ ප්‍රස්ථාර (එකම අක්ෂවල). සංඛ්‍යාත්මක සහ විශ්ලේෂණාත්මක විසඳුම් අතර වෙනස පිළිබඳ ප්‍රස්තාරය. කැළඹුණු සංඛ්‍යාත්මක විසඳුම්වල ප්‍රස්තාර සහ කැළඹුණු සහ නොකැළඹුණු විසඳුම් අතර වෙනස: අ) ආරම්භක තත්ත්වය කැළඹී ඇති විට; b) දකුණු පැත්ත කැළඹී ඇති විට. මායිම් අගය ගැටලුවේ කොන්දේසිය පිළිබඳ නිගමනය.

සමීකරණය වර්ගය

සමහර සංඛ්‍යා කොහිද, නියත සංගුණක සහිත රේඛීය වෙනස සමීකරණයක් ලෙස හැඳින්වේ.

සාමාන්‍යයෙන්, (1) සමීකරණය වෙනුවට, පරිමිත වෙනස්කම්වල සිට ශ්‍රිතයේ අගය වෙත ගමන් කිරීමෙන් (1) වෙතින් ලබා ගන්නා සමීකරණයක් සලකනු ලැබේ, එනම් පෝරමයේ සමීකරණයකි.

(2) සමීකරණයේ ශ්‍රිතයක් තිබේ නම්, එවැනි සමීකරණයක් සමජාතීය ලෙස හැඳින්වේ.

සමජාතීය සමීකරණය සලකා බලන්න

රේඛීය වෙනස්කම් සමීකරණ න්‍යාය රේඛීය අවකල සමීකරණ න්‍යායට සමාන වේ.

ප්රමේයය 1.

ශ්‍රිත සමජාතීය සමීකරණයේ (3) විසඳුම් නම්, ශ්‍රිතය

(3) සමීකරණයට ද විසඳුමකි.

සාක්ෂි.

(3) හි ඇති කාර්යයන් ආදේශ කරන්න

ශ්‍රිතය සමීකරණයට විසඳුමක් වන බැවින් (3).

එවැනි සංඛ්‍යා තිබේ නම් දැලිස් ශ්‍රිත රේඛීයව යැපෙන ලෙස හැඳින්වේ. අවම වශයෙන් එකක් ශුන්‍ය නොවන විට, පහත සඳහන් ඕනෑම එකක් සත්‍ය වේ:

(4)

(4) සඳහා පමණක් පවතී නම් එවිට ශ්‍රිත, රේඛීය ස්වාධීන ලෙස හැඳින්වේ.

සම (3) හි ඕනෑම k රේඛීය ස්වාධීන විසඳුම් මූලික විසඳුම් පද්ධතියක් සාදයි.

(3) සමීකරණයේ රේඛීය ස්වාධීන විසඳුම් වලට ඉඩ දෙන්න

(3) සමීකරණයේ පොදු විසඳුමකි. නිශ්චිත කොන්දේසියක් සොයාගත් විට, එය ආරම්භක කොන්දේසි වලින් තීරණය වේ

අපි පෝරමයේ (3) සමීකරණයට විසඳුමක් සොයමු:

සමීකරණයට ආදේශ කරන්න (3)

අපි සමීකරණය (5) බෙදන්නෙමු

ලාක්ෂණික සමීකරණය. (6)

(6) ඇත්තේ සරල මූලයන් පමණක් යැයි උපකල්පනය කරමු එය තහවුරු කිරීම පහසුය රේඛීයව ස්වාධීන වේ. සමජාතීය සමීකරණයේ පොදු විසඳුම (3) ආකෘතිය ඇත

උදාහරණයක්.

සමීකරණය සලකා බලන්න

ලාක්ෂණික සමීකරණයට ස්වරූපය ඇත

විසඳුම පෙනෙන්නේ

මූලයට බහු ගුණයක් තිබිය යුතුය r. මෙම මූල ද්රාවණයට අනුරූප වේ

ඉතිරි මුල් බව උපකල්පනය කරයි බහු නොවේ, එවිට සම (3) හි සාමාන්‍ය විසඳුමේ ස්වරූපය ඇත

සමජාතීය සමීකරණයේ (2) පොදු විසඳුම සලකා බලන්න.

සමජාතීය සමීකරණයේ විශේෂ විසඳුම (2), පසුව පොදු විසඳුම

දේශනය 16

දේශන සැලැස්ම

1. D සහ Z සංකල්පය - පරිවර්තනයන්.

2. D සහ Z හි විෂය පථය - පරිවර්තනයන්.

3. ප්රතිලෝම D සහ Z - පරිවර්තනයන්.

ඩිස්ක්‍රීට් ලැප්ලේස් ට්‍රාන්ස්ෆෝම්.

Z - පරිවර්තනය.

දැලිස් ශ්‍රිත භාවිතයට අදාළ ව්‍යවහාරික පර්යේෂණ වලදී, විවික්ත ලැප්ලේස් ට්‍රාන්ස්ෆෝම් (D-transform) සහ Z-transform බහුලව භාවිතා වේ. සාමාන්‍ය ලැප්ලේස් පරිණාමනය සමඟ ප්‍රතිසමයෙන්, විවික්ත එකක් ස්වරූපයෙන් ලබා දී ඇත

කොහෙද (1)

සංකේතාත්මකව D - පරිවර්තනය ලෙස ලියා ඇත

මාරු කළ දැලිස් කාර්යයන් සඳහා

කොහෙද ඕෆ්සෙට් එක.

Z - පරිවර්තනය D - පරිවර්තනයෙන් ආදේශ කිරීම මගින් ලබා ගන්නා අතර සම්බන්ධතාවය මගින් ලබා දේ

(3)

පක්ෂග්රාහී කාර්යයක් සඳහා

ශ්‍රිතයක් මුල් if ලෙස හැඳින්වේ

2) වර්ධන දර්ශකයක් ඇත, එනම් එවැනි සහ එවැනි ඒවා තිබේ

(4)

අසමානතාවය (4) සත්‍ය වන සංඛ්‍යා වලින් කුඩාම (හෝ කුඩාම සංඛ්‍යාව නැඹුරු වන සීමාව) නිරපේක්ෂ අභිසාරීතාවයේ abscissa ලෙස හඳුන්වනු ලබන අතර එය දැක්වේ.

ප්රමේයය.

ශ්‍රිතය මුල් පිටපත නම්, රූපය Re p > ප්‍රදේශයෙන් අර්ථ දක්වා ඇති අතර එය මෙම ප්‍රදේශයේ විශ්ලේෂණ ශ්‍රිතයකි.

අපි Re p > ශ්‍රේණි (1) සඳහා නිරපේක්ෂ වශයෙන් අභිසාරී වන බව පෙන්වමු. අපිට තියනවා

නිශ්චිත ප්‍රමාණය දර්ශකයක් සහිත අඩුවන ජ්‍යාමිතික ප්‍රගතියක ​​සාමාජිකයින්ගේ එකතුව වන බැවින් එවැනි ප්රගතියක් අභිසාරී වන බව දන්නා කරුණකි. අගය අත්තනෝමතික ලෙස අගයට ආසන්නව ගත හැකිය, එනම් ප්‍රමේයයේ පළමු කොටස ඔප්පු කර ඇත.

අපි ප්‍රමේයයේ දෙවන කොටස ඔප්පු කිරීමකින් තොරව පිළිගනිමු.

රූපය යනු මනඃකල්පිත කාල පරිච්ඡේදයක් සහිත ආවර්තිතා ශ්රිතයකි

රූපයක් අධ්‍යයනය කරන විට, එය සම්පූර්ණ සංකීර්ණ තලය මත සලකා බැලීම තේරුමක් නැත, පළලක් සහිත ඕනෑම තීරුවක අධ්‍යයනය කිරීමට අපව සීමා කිරීම ප්‍රමාණවත් වේ. ප්රධාන ලෙස හැඳින්වේ. බව. රූප බිම තීරුවේ අර්ථ දක්වා ඇති බව අපට උපකල්පනය කළ හැකිය

සහ මෙම අර්ධ තීරුවේ විශ්ලේෂණ කාර්යයකි.

සැකසීමෙන් F(z) ශ්‍රිතයේ නිර්වචනය සහ විශ්ලේෂණ වසම අපි සොයා ගනිමු. අපි අර්ධ තීරුව බව පෙන්වමු තලය p තලයේ කලාපයක් බවට පරිවර්තනය වේ z: .

ඇත්ත වශයෙන්ම, කොටස , p-තලය මත අර්ධ තීරුව සීමා කරන, z-තලය මත අසල්වැසි බවට පරිවර්තනය කර ඇත: .

පරිවර්තනය කොටස පරිවර්තනය කරන රේඛාවෙන් දක්වන්න . ඉන්පසු

අසල්වාසී.

බව. Z – පරිවර්තනය F(z) වසම තුළ අර්ථ දක්වා ඇති අතර එය මෙම වසමේ විශ්ලේෂණ ශ්‍රිතයකි.

ප්රතිලෝම D - පරිවර්තනය මඟින් රූපයෙන් දැලිස් ශ්රිතය ප්රතිෂ්ඨාපනය කිරීමට ඔබට ඉඩ සලසයි

(5)

අපි සමානාත්මතාවය ඔප්පු කරමු.

ඔවුන් අසල්වැසි ප්රදේශය තුළ වැතිර සිටිති.

(7)

(8)

සමානාත්මතා (7) සහ (8) වලදී, F(s) ශ්‍රිතයේ සියලුම ඒකීය ලක්ෂ්‍යයන් මත අවශේෂ ලබා ගනී.