Лінійна залежність незалежність. Лінійно залежні та лінійно незалежні вектори

Щоб перевірити чи є система векторів лінійно-залежної, необхідно скласти лінійну комбінацію цих векторів і перевірити, чи може вона бути рана нулю, якщо хоч один коефіцієнт дорівнює нулю.

Випадок 1. Система векторів задана векторами

Складаємо лінійну комбінацію

Ми отримали однорідну систему рівнянь. Якщо вона має ненульове рішення, то визначник повинен дорівнювати нулю. Складемо визначник та знайдемо його значення.

Визначник дорівнює нулю, отже вектори лінійно залежні.

Випадок 2. Система векторів задана аналітичними функціями:

a)
, якщо тотожність вірна, значить система лінійно залежна.

Складемо лінійну комбінацію.

Необхідно перевірити, чи існують такі a, b, c (хоча б одна з яких не дорівнює нулю) при яких цей вираз дорівнює нулю.

Запишемо гіперболічні функції

,
тоді

тоді лінійна комбінація векторів набуде вигляду:

Звідки
, Візьмемо, наприклад, тоді лінійна комбінація дорівнює нулю, отже, система лінійно залежна.

Відповідь: система лінійно залежна.

b)
складемо лінійну комбінацію

Лінійна комбінація векторів повинна дорівнювати нулю для будь-яких значень x.

Перевіримо для окремих випадків.

Лінійна комбінація векторів дорівнює нулю, тільки якщо всі коефіцієнти дорівнюють нулю.

Отже система лінійно не залежна.

Відповідь: система лінійно не залежить.

5.3. Знайти якийсь базис та визначити розмірність лінійного простору рішень.

Сформуємо розширену матрицю і наведемо її до виду трапеції методом Гаусса.

Щоб отримати який-небудь базис підставимо довільні значення:

Отримаємо інші координати

Відповідь:

5.4. Знайти координати вектора X у базисі, якщо він заданий у базисі.

Знаходження координат вектора у новому базисі зводиться до вирішення системи рівнянь

Спосіб 1. Знаходження за допомогою матриці переходу

Складемо матрицю переходу

Знайдемо вектор у новому базисі за формулою

Знайдемо зворотну матрицю та виконаємо множення

,

Спосіб 2. Знаходження шляхом складання системи рівнянь.

Складемо базисні вектори з коефіцієнтів базису

,
,

Знаходження вектора у новому базисі має вигляд

, де dце заданий вектор x.

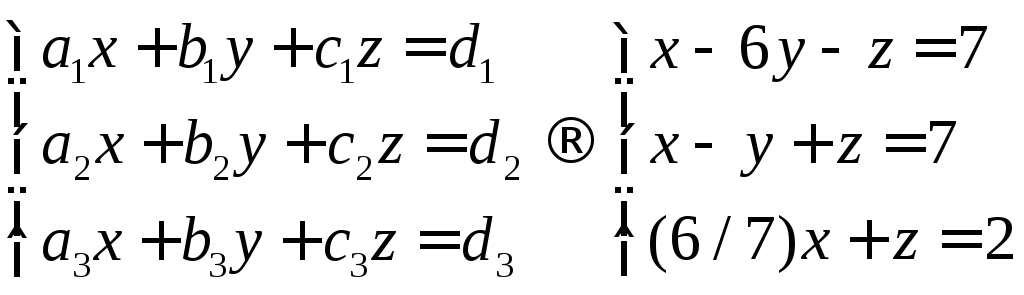
Отримане рівняння можна вирішити будь-яким способом, відповідь буде аналогічною.

Відповідь: вектор у новому базисі
.

5.5. Нехай x = (x 1 , x 2 , x 3 ) . Чи є лінійними такі перетворення.

Складемо матриці лінійних операторів із коефіцієнтів заданих векторів.

Перевіримо властивість лінійних операцій кожної матриці лінійного оператора.

Ліву частину знайдемо множенням матриці Ана вектор

Праву частину знайдемо, помноживши заданий вектор на скаляр
.

Ми бачимо, що
отже, перетворення перестав бути лінійним.

Перевіримо інші вектори.

, Перетворення не є лінійним.

, Перетворення є лінійним.

Відповідь: Ах– не лінійне перетворення, Вх- Не лінійне, Сх- Лінійне.

Примітка.Можна виконати це завдання набагато простіше, уважно подивившись на задані вектори. У Ахми бачимо, що є доданки, які не містять елементи хщо не могло бути отримано в результаті лінійної операції. У Вхє елемент хтретього ступеня, що також не могло бути отримано множенням на вектор х.

5.6. Дано x = { x 1 , x 2 , x 3 } , Ax = { x 2 – x 3 , x 1 , x 1 + x 3 } , Bx = { x 2 , 2 x 3 , x 1 } . Виконати задану операцію: ( A ( B – A )) x .

Випишемо матриці лінійних операторів.

Виконаємо операцію над матрицями

При множенні отриманої матриці на Х отримаємо

Відповідь:

Завдання 1.З'ясувати, чи система векторів лінійно незалежної. Систему векторів задаватимемо матрицею системи, стовпці якої складаються з координат векторів.

.

Рішення.Нехай лінійна комбінація дорівнює нулю. Записавши цю рівність у координатах, отримаємо таку систему рівнянь:

.

Така система рівнянь називається трикутною. Вона має єдине рішення . Отже, вектори лінійно незалежні.

Завдання 2.З'ясувати, чи є лінійно незалежною система векторів.

.

Рішення.Вектори лінійно незалежні (див. Завдання 1). Доведемо, що вектор є лінійною комбінацією векторів . Коефіцієнти розкладання за векторами визначаються із системи рівнянь

.

Ця система як трикутна має єдине рішення.

Отже, система векторів лінійно залежна.

Зауваження. Матриці, такого виду, як у задачі 1, називаються трикутними , а задачі 2 – східчасто-трикутними . Питання лінійної залежності системи векторів легко вирішується, якщо матриця, складена з координат цих векторів, є східчасто трикутною. Якщо матриця не має спеціального виду, то за допомогою елементарних перетворень рядків , Що зберігають лінійні співвідношення між стовпцями, її можна привести до східчасто-трикутного вигляду.

Елементарними перетвореннями рядківматриці (ЕПС) називаються наступні операції над матрицею:

1) перестановка рядків;

2) множення рядка на відмінне від нуля число;

3) додавання до рядка іншого рядка, помноженого на довільне число.

Завдання 3.Знайти максимальну лінійно незалежну підсистему та обчислити ранг системи векторів

.

Рішення.Наведемо матрицю системи за допомогою ЕПС до східчасто-трикутного вигляду. Щоб пояснити порядок дій, рядок з номером матриці, що перетворюється, позначимо символом . У стовпці після стрілки вказані дії над рядками матриці, які потрібно виконати для отримання рядків нової матриці.

.

Очевидно, що перші два стовпці отриманої матриці лінійно незалежні, третій стовпець є їхньою лінійною комбінацією, а четвертий не залежить від двох перших. Вектори називаються базисними. Вони утворюють максимальну лінійно незалежну підсистему системи , А ранг системи дорівнює трьом.

Базис, координати

Завдання 4.Знайти базис та координати векторів у цьому базисі на безлічі геометричних векторів, координати яких задовольняють умові .

Рішення. Багато є площиною, що проходить через початок координат. Довільний базис на площині складається із двох неколлінеарних векторів. Координати векторів у вибраному базисі визначаються розв'язком відповідної системи лінійних рівнянь.

Існує й інший спосіб вирішення цього завдання, коли знайти базис можна за координатами.

Координати простори є координатами на площині , оскільки пов'язані співвідношенням тобто не є незалежними. Незалежні змінні і (вони називаються вільними) однозначно визначають вектор на площині і, отже, можуть бути обрані координатами в . Тоді базис складається з векторів, що лежать у відповідних наборах вільних змінних і , тобто .

Завдання 5.Знайти базис і координати векторів у цьому базисі на багатьох векторів простору , у яких непарні координати рівні між собою.

Рішення. Виберемо, як і в попередній задачі, координати у просторі .

Так як , то вільні змінні однозначно визначають вектор і, отже, є координатами. Відповідний базис складається з векторів.

Завдання 6.Знайти базис і координати векторів у цьому базисі на безлічі всіх матриць виду , де - Довільні числа.

Рішення. Кожна матриця з однозначно представлена ​​у вигляді:

Це співвідношення є розкладанням вектора з базису
з координатами .

Завдання 7.Знайти розмірність та базис лінійної оболонки системи векторів

.

Рішення.Перетворимо за допомогою ЕПС матрицю з координат векторів системи до східчасто-трикутного вигляду.

.

Стовпці останньої матриці лінійно незалежні, а стовпці лінійно виражаються крізь них. Отже, вектори утворюють базис , і .

Зауваження. Базис у вибирається неоднозначно. Наприклад, вектори також утворюють базис .

У цій статті ми розповімо:

• що таке колінеарні вектори;
• які існують умови колінеарності векторів;
• які існують властивості колінеарних векторів;
• що таке лінійна залежність колінеарних векторів

Yandex.RTB R-A-339285-1 Визначення 1

Колінеарні вектори – це вектори, які є паралелями однієї прямої або лежать на одній прямій.

Приклад 1

Умови колінеарності векторів

Два вектори є колінеарними, якщо виконується будь-яка з наступних умов:

• умова 1 . Вектори a і b колінеарні за наявності такого числа λ, що a = b;
• умова 2 . Вектори a і b колінеарні при рівному відношенні координат:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a b ⇔ a 1 b 1 = a 2 b 2

• умова 3 . Вектори a та b колінеарні за умови рівності векторного твору та нульового вектора:

a b ⇔ a , b = 0

Зауваження 1

Умова 2 не застосовується, якщо одна з координат вектора дорівнює нулю.

Зауваження 2

Умова 3 застосовується лише до тих векторів, які в просторі.

Приклади завдань дослідження коллінеарності векторів

Приклад 1

Досліджуємо вектори а = (1; 3) і b = (2; 1) на колінеарність.

Як вирішити?

У даному випадкунеобхідно скористатися 2 умовою коллінеарності. Для заданих векторів воно виглядає так:

Рівність неправильна. Звідси можна дійти невтішного висновку, що вектори a і b неколлинеарны.

Відповідь : a | | b

Приклад 2

Яке значення m вектора a = (1; 2) і b = (- 1; m) необхідне для колінеарності векторів?

Як вирішити?

Використовуючи другу умову коллінераності, вектори будуть колінеарними, якщо їх координати будуть пропорційними:

Звідси видно, що m = -2.

Відповідь: m = -2.

Критерії лінійної залежності та лінійної незалежності систем векторів

Теорема

Система векторів векторного простору лінійно залежить тільки у тому випадку, коли один із векторів системи можна виразити через інші вектори даної системи.

Доведення

Нехай система e 1, e 2,. . . , n є лінійно залежною. Запишемо лінійну комбінацію цієї системи рівну нульовому вектору:

a 1 e 1 + a 2 e 2 +. . . + a n e n = 0

в якій хоча б один із коефіцієнтів комбінації не дорівнює нулю.

Нехай a k ≠ 0 k ∈ 1, 2, . . . , n.

Ділимо обидві частини рівності на ненульовий коефіцієнт:

a k - 1 (a k - 1 a 1) e 1 + (ak - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Позначимо:

Ak - 1 a m , де m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

В такому випадку:

β 1 e 1 +. . . + β k - 1 e k - 1 + β k + 1 e k + 1 +. . . + β n e n = 0

або e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Звідси випливає, що один із векторів системи виражається через всі інші вектори системи. Що потрібно було довести (ч.т.д.).

Достатність

Нехай один із векторів можна лінійно виразити через решту векторів системи:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

Переносимо вектор e k праву частинуцієї рівності:

0 = γ 1 e 1 +. . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

Оскільки коефіцієнт вектора e k дорівнює -1 ≠ 0, у нас виходить нетривіальне уявлення нуля системою векторів e1, e2,. . . , e n , а це, у свою чергу, означає, що дана системавектори лінійно залежні. Що потрібно було довести (ч.т.д.).

Наслідок:

• Система векторів є лінійно незалежною, коли жоден із її векторів не можна виразити через решту векторів системи.
• Система векторів, яка містить нульовий вектор або два рівні вектори, лінійно залежна.

Властивості лінійно залежних векторів

1. Для 2-х і 3-х мірних векторів виконується умова: два лінійно залежні вектори - колінеарні. Два колінеарні вектори - лінійно залежні.
2. Для 3-х мірних векторів виконується умова: три лінійно залежні вектор- Компланарні. (3 компланарні вектори - лінійно залежні).
3. Для n-вимірних векторів виконується умова: n + 1 вектор завжди лінійно залежні.

Приклади розв'язання задач на лінійну залежність або лінійну незалежність векторів

Приклад 3

Перевіримо вектори a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 на лінійну незалежність.

Рішення. Вектори є лінійно залежними, оскільки розмірність векторів менша за кількість векторів.

Приклад 4

Перевіримо вектори a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 на лінійну незалежність.

Рішення. Знаходимо значення коефіцієнтів, при яких лінійна комбінація дорівнюватиме нульовому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записуємо векторне рівняння у вигляді лінійного:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Вирішуємо цю систему за допомогою методу Гауса:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

З 2-го рядка віднімаємо 1-й, з 3-го - 1-й:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

З 1-го рядка віднімаємо 2-й, до 3-го додаємо 2-й:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

З рішення випливає, що система має безліч рішень. Це означає, що є ненульова комбінація значення таких чисел x 1 , x 2 , x 3 , у яких лінійна комбінація a , b , c дорівнює нульовому вектору. Отже, вектори a, b, c є лінійно залежними.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Вектори, їх властивості та дії з ними

Векторні дії з векторами, лінійний векторний простір.

Вектори-упорядкована сукупність кінцевої кількості дійсних чисел.

Дії: 1.Умножение вектора на число: лямда*вектор х=(лямда*х 1 , лямда*х 2 … лямда*х n).(3,4, 0, 7)*3=(9, 12,0,21)

2.Складання векторів (належать тому самому векторному простору) вектор х+вектор у = (х 1 +у 1, х 2 +у 2, … х n +у n ,)

3. Вектор 0=(0,0…0)--n E n – n-мірний (лінійний простір) вектор х +вектор 0 = вектор х

Теорема. Для того, щоб система n векторів, n-мірного лінійного простору була лінійно залежною, необхідно і достатньо, щоб один із векторів були лінійною комбінацією іншим.

Теорема. Будь-яка сукупність n+ 1ого вектора n-мірного лінійного простору явл. лінійно залежною.

Додавання векторів, множення векторів на числа. Віднімання векторів.

Сумою двох векторів називається вектор, спрямований з початку вектора в кінець вектора за умови, що початок збігається з кінцем вектора. Якщо вектори задані їх розкладаннями по базисним ортам, при складанні векторів складаються їх відповідні координати.

Розглянемо це з прикладу декартової системи координат. Нехай

Покажемо, що

З малюнка 3 видно, що

Сума будь-якого кінцевого числа векторів може бути знайдена за правилом багатокутника (рис. 4): щоб побудувати суму кінцевого числа векторів, достатньо поєднати початок кожного наступного вектора з кінцем попереднього та побудувати вектор, що з'єднує початок першого вектора з кінцем останнього.

Властивості операції складання векторів:

У цих виразах m, n – числа.

Різницею векторів називають вектор Друге доданок є вектором, протилежним вектору за напрямом, але рівним йому по довжині.

Таким чином, операція віднімання векторів замінюється на операцію складання

Вектор, початок якого знаходиться на початку координат, а кінець - у точці А (x1, y1, z1) називають радіус-вектором точки А і позначають або просто. Оскільки його координати збігаються з координатами точки А, його розкладання по ортам має вигляд

Вектор, що має початок у точці А(x1, y1, z1) та кінець у точці B(x2, y2, z2), може бути записаний у вигляді

де r 2 - радіус-вектор точки; r 1 – радіус-вектор точки А.

Тому розкладання вектора по ортах має вигляд

Його довжина дорівнює відстані між точками А та В

УМНОЖЕННЯ

Так, у разі плоскої задачі добуток вектор на a = (ax; ay) на число b знаходиться за формулою

a · b = (ax · b; ay · b)

Приклад 1. Знайти добуток вектора a = (1; 2) на 3.

3 · a = (3 · 1; 3 · 2) = (3; 6)

Так, у разі просторового завдання добуток вектора a = (ax; ay; az) на число b знаходиться за формулою

a · b = (ax · b; ay · b; az · b)

Приклад 1. Знайти добуток вектора a = (1; 2; -5) на 2.

2 · a = (2 · 1; 2 · 2; 2 · (-5)) = (2; 4; -10)

Скалярний добуток векторів та де - Кут між векторами і; якщо або , то

З визначення скалярного твору випливає, що

де, наприклад, є величина проекції вектора напрям вектора .

Скалярний квадрат вектор:

Властивості скалярного твору:

Скалярний твір у координатах

Якщо то

Кут між векторами

Кут між векторами – кут між напрямками цих векторів (найменший кут).

Векторний твір (Векторний твір двох векторів)це псевдовектор, перпендикулярний до площини, побудованої по двох співмножниках, що є результатом бінарної операції «векторне множення» над векторами в тривимірному Евклідовому просторі. Твір не є ні коммутативним, ні асоціативним (він є антикомутативним) і відрізняється від скалярного твору векторів. У багатьох завданнях інженерії та фізики потрібно мати можливість будувати вектор, перпендикулярний двом наявним. векторний витвірнадає цю можливість. Векторний добуток корисний для «вимірювання» перпендикулярності векторів - довжина векторного добутку двох векторів дорівнює добутку їх довжин, якщо вони перпендикулярні, і зменшується до нуля, якщо вектори паралельні або антипаралельні.

Векторний твір визначено лише у тривимірному та семимірному просторах. Результат векторного твору, як і скалярного, залежить від метрики Евклідова простору.

На відміну від формули для обчислення за координатами векторів скалярного твору в тривимірній прямокутній системі координат формула для векторного твору залежить від орієнтації прямокутної системикоординат чи, інакше, її «хіральності»

Колінеарність векторів.

Два ненульові (не рівні 0) вектори називаються колінеарними, якщо вони лежать на паралельних прямих або на одній прямій. Допустимо, але не рекомендується синонім - «паралельні» вектори. Колінеарні вектори можуть бути однаково спрямовані ("соннаправлені") або протилежно спрямовані (в останньому випадку їх іноді називають "антиколлінеарними" або "антипаралельними").

Змішане вироблення векторів( a, b, c)- скалярний добуток вектора на векторний добуток векторів b і c:

(a, b, c) = a ⋅ (b × c)

іноді його називають потрійним скалярним творомвекторів, мабуть через те, що результатом є скаляр (точніше - псевдоскаляр).

Геометричний зміст: Модуль змішаного твору чисельно дорівнює обсягу паралелепіпеда, утвореного векторами (a, b, c) .

Властивості

Змішане твір кососиметрично по відношенню до всіх своїх аргументів:т. е. перестановка будь-яких двох співмножників змінює знак твору. Звідси випливає, що Змішаний добуток у правій декартовій системі координат (в ортонормованому базисі) дорівнює визначнику матриці, складеної з векторів і:

Змішаний добуток у лівій декартовій системі координат (в ортонормованому базисі) дорівнює визначнику матриці, складеної з векторів і взятому зі знаком "мінус":

Зокрема,

Якщо будь-які два вектори паралельні, то з будь-яким третім вектором вони утворюють змішаний твір, що дорівнює нулю.

Якщо три вектори лінійно залежні (тобто компланарні, лежать у одній площині), їх змішаний твір дорівнює нулю.

Геометричний зміст - Змішане твір за абсолютним значенням дорівнює обсягу паралелепіпеда (див. малюнок), утвореного векторами і; знак залежить від того, чи є ця трійка векторів правою чи лівою.

Компланарність векторів.

Три вектори (або більше) називаються компланарними, якщо вони, будучи приведеними до загального початку, лежать в одній площині

Властивості компланарності

Якщо хоча б один із трьох векторів- нульовий, то три вектори також вважаються компланарними.

Трійка векторів, що містить пару колінеарних векторів, є компланарною.

Змішане твір компланарних векторів. Це критерій компланарності трьох векторів.

Компланарні вектори – лінійно залежні. Це – також критерій компланарності.

У 3-мірному просторі 3 некомпланарні вектори утворюють базис

Лінійно залежні та лінійно незалежні вектори.

Лінійно залежні та незалежні системивекторів.Визначення. Система векторів називається лінійно залежноюякщо існує хоча б одна нетривіальна лінійна комбінація цих векторів, що дорівнює нульовому вектору. Інакше, тобто. якщо тільки тривіальна лінійна комбінація даних векторів дорівнює нульовому вектору, вектори називаються лінійно незалежними.

Теорема (критерій лінійної залежності). Для того щоб система векторів лінійного простору була лінійно залежною, необхідно і достатньо, щоб, принаймні, один із цих векторів був лінійною комбінацією інших.

1) Якщо серед векторів є хоча б один нульовий вектор, то вся система векторів є лінійно залежною.

Справді, якщо, наприклад, то, вважаючи, маємо нетривіальну лінійну комбінацію.

2) Якщо серед векторів деякі утворюють лінійно залежну систему, то вся система лінійно залежна.

Справді, нехай вектори , лінійно залежні. Отже, існує нетривіальна лінійна комбінація, що дорівнює нульовому вектору. Але тоді, гадаючи отримаємо також нетривіальну лінійну комбінацію , рівну нульовому вектору.

2. Базис та розмірність. Визначення. Система лінійно незалежних векторів векторного простору називається базисомцього простору, якщо будь-який вектор може бути представлений у вигляді лінійної комбінації векторів цієї системи, тобто. для кожного вектора існують дійсні числа такі, що має місце рівність Ця рівність називається розкладання вектораза базисом , а числа називаються координатами вектора щодо базису(або у базисі) .

Теорема (про єдиність розкладання за базисом). Кожен вектор простору може бути розкладений за базисом. єдиним чином, тобто. координати кожного вектора у базисі визначаються однозначно.