Ajouter une fraction décimale fractionnaire. Décimales : définitions, notation, exemples, actions avec des décimales

Parmi les nombreuses fractions trouvées en arithmétique, celles avec 10, 100, 1000 au dénominateur méritent une attention particulière - en général, toute puissance de dix. Ces fractions ont un nom et une notation spéciaux.

Un nombre décimal est un nombre dont le dénominateur est une puissance de dix.

Exemples décimaux :

Pourquoi était-il nécessaire d'isoler de telles fractions ? Pourquoi ont-ils besoin de leur propre formulaire d'inscription? Il y a au moins trois raisons à cela :

1. Les nombres décimaux sont beaucoup plus faciles à comparer. Rappel : à titre de comparaison fractions ordinaires ils doivent être soustraits les uns des autres et, en particulier, réduire les fractions à dénominateur commun. Dans les fractions décimales, rien de tout cela n'est requis ;
2. Réduction des calculs. Les nombres décimaux s'additionnent et se multiplient selon leurs propres règles, et avec un peu de pratique, vous pourrez travailler avec eux beaucoup plus rapidement qu'avec les nombres ordinaires ;
3. Facilité d'enregistrement. Contrairement aux fractions ordinaires, les décimales sont écrites sur une seule ligne sans perte de clarté.

La plupart des calculatrices donnent également des réponses en décimales. Dans certains cas, un format d'enregistrement différent peut causer des problèmes. Par exemple, que se passe-t-il si vous demandez un changement d'un montant de 2/3 de roubles dans un magasin :)

Règles d'écriture des fractions décimales

Le principal avantage des fractions décimales est une notation pratique et visuelle. À savoir:

La notation décimale est une forme de notation décimale où la partie entière est séparée de la partie fractionnaire à l'aide d'un point ou d'une virgule. Dans ce cas, le séparateur lui-même (point ou virgule) est appelé le point décimal.

Par exemple, 0,3 (lire : "zéro entier, 3 dixièmes") ; 7,25 (7 entiers, 25 centièmes) ; 3,049 (3 entiers, 49 millièmes). Tous les exemples sont tirés de la définition précédente.

En écriture, une virgule est généralement utilisée comme point décimal. Ici et ci-dessous, la virgule sera également utilisée dans tout le site.

Pour écrire une fraction décimale arbitraire sous la forme spécifiée, vous devez suivre trois étapes simples :

1. Écrivez le numérateur séparément;
2. Décaler la virgule vers la gauche d'autant de positions qu'il y a de zéros au dénominateur. Supposons qu'initialement la virgule décimale se trouve à droite de tous les chiffres ;
3. Si la virgule décimale s'est déplacée et qu'il y a ensuite des zéros à la fin de l'enregistrement, ils doivent être barrés.

Il arrive qu'à la deuxième étape, le numérateur n'ait pas assez de chiffres pour terminer le décalage. Dans ce cas, les positions manquantes sont remplies de zéros. Et en général, n'importe quel nombre de zéros peut être attribué à gauche de n'importe quel nombre sans nuire à la santé. C'est moche, mais parfois utile.

À première vue, cet algorithme peut sembler assez compliqué. En fait, tout est très, très simple - il suffit de s'entraîner un peu. Jetez un œil aux exemples :

Une tâche. Pour chaque fraction, indiquez sa notation décimale :

Le numérateur de la première fraction : 73. Nous décalons la virgule décimale d'un signe (car le dénominateur est 10) - nous obtenons 7,3.

Le numérateur de la deuxième fraction : 9. Nous décalons la virgule décimale de deux chiffres (car le dénominateur est 100) - nous obtenons 0,09. J'ai dû ajouter un zéro après la virgule et un de plus avant, pour ne pas laisser une notation étrange comme ".09".

Le numérateur de la troisième fraction : 10029. Nous décalons la virgule décimale de trois chiffres (car le dénominateur est 1000) - nous obtenons 10,029.

Le numérateur de la dernière fraction : 10500. Encore une fois, nous décalons le point de trois chiffres - nous obtenons 10,500. Il y a des zéros supplémentaires à la fin du nombre. Nous les barrons - nous obtenons 10,5.

Faites attention aux deux derniers exemples : les nombres 10.029 et 10.5. Selon les règles, les zéros à droite doivent être barrés, comme cela se fait dans dernier exemple. Cependant, vous ne devez en aucun cas le faire avec des zéros à l'intérieur du nombre (qui sont entourés d'autres chiffres). C'est pourquoi nous avons obtenu 10,029 et 10,5, et non 1,29 et 1,5.

Nous avons donc compris la définition et la forme d'enregistrement des fractions décimales. Découvrons maintenant comment convertir des fractions ordinaires en décimales - et vice versa.

Passer des fractions aux décimales

Considérons une simple fraction numérique de la forme a / b . Vous pouvez utiliser la propriété de base d'une fraction et multiplier le numérateur et le dénominateur par un nombre tel que vous obtenez une puissance de dix ci-dessous. Mais avant cela, veuillez lire ce qui suit :

Il y a des dénominateurs qui ne se réduisent pas à la puissance dix. Apprenez à reconnaître ces fractions, car elles ne peuvent pas être travaillées selon l'algorithme décrit ci-dessous.

C'est ça. Eh bien, comment comprendre si le dénominateur est réduit à la puissance dix ou non ?

La réponse est simple : factoriser le dénominateur en facteurs premiers. Si seuls les facteurs 2 et 5 sont présents dans le développement, ce nombre peut être réduit à la puissance dix. S'il y a d'autres nombres (3, 7, 11 - peu importe), vous pouvez oublier le degré de dix.

Une tâche. Vérifiez si les fractions spécifiées peuvent être représentées sous forme de décimales :

Nous écrivons et factorisons les dénominateurs de ces fractions :

20 \u003d 4 5 \u003d 2 2 5 - seuls les nombres 2 et 5 sont présents.Par conséquent, la fraction peut être représentée sous forme décimale.

12 \u003d 4 3 \u003d 2 2 3 - il existe un facteur "interdit" 3. La fraction ne peut pas être représentée sous forme décimale.

640 \u003d 8 8 10 \u003d 2 3 2 3 2 5 \u003d 2 7 5. Tout est en ordre : il n'y a rien sauf les chiffres 2 et 5. Une fraction est représentée sous forme décimale.

48 \u003d 6 8 \u003d 2 3 2 3 \u003d 2 4 3. Le facteur 3 a "refait surface" à nouveau, il ne peut pas être représenté comme une fraction décimale.

Nous avons donc compris le dénominateur - nous allons maintenant considérer l'ensemble de l'algorithme de passage aux fractions décimales :

1. Factorisez le dénominateur de la fraction d'origine et assurez-vous qu'il est généralement représentable sous forme décimale. Ceux. vérifier que seuls les facteurs 2 et 5 sont présents dans le développement, sinon l'algorithme ne fonctionne pas ;
2. Comptez combien de deux et de cinq sont présents dans la décomposition (il n'y aura pas d'autres nombres là-bas, souvenez-vous ?). Choisissez un tel multiplicateur supplémentaire pour que le nombre de deux et de cinq soit égal.
3. En fait, multipliez le numérateur et le dénominateur de la fraction d'origine par ce facteur - nous obtenons la représentation souhaitée, c'est-à-dire le dénominateur sera une puissance de dix.

Bien sûr, le facteur supplémentaire sera également décomposé uniquement en deux et en cinq. Dans le même temps, afin de ne pas vous compliquer la vie, vous devez choisir le plus petit facteur de ce type parmi tous les facteurs possibles.

Et encore une chose: s'il y a une partie entière dans la fraction d'origine, assurez-vous de convertir cette fraction en une fraction impropre - et ensuite seulement appliquez l'algorithme décrit.

Une tâche. Convertissez ces nombres en décimaux :

Factorisons le dénominateur de la première fraction : 4 = 2 · 2 = 2 2 . Par conséquent, une fraction peut être représentée sous la forme d'un nombre décimal. Il y a deux deux et pas de cinq dans le développement, donc le facteur supplémentaire est 5 2 = 25. Le nombre de deux et de cinq lui sera égal. Nous avons:

Passons maintenant à la deuxième fraction. Pour ce faire, notez que 24 \u003d 3 8 \u003d 3 2 3 - il y a un triple dans l'expansion, donc la fraction ne peut pas être représentée sous forme décimale.

Les deux dernières fractions ont pour dénominateurs 5 (un nombre premier) et 20 = 4 5 = 2 2 5 respectivement - seuls deux et cinq sont présents partout. En même temps, dans le premier cas, "pour un bonheur complet", il n'y a pas assez de multiplicateur 2, et dans le second - 5. On obtient :

Passer des décimaux à l'ordinaire

La conversion inverse - de la notation décimale à la normale - est beaucoup plus facile. Il n'y a pas de restrictions ni de contrôles spéciaux, vous pouvez donc toujours convertir une fraction décimale en une fraction classique "à deux étages".

L'algorithme de traduction est le suivant :

1. Barrez tous les zéros à gauche de la virgule, ainsi que la virgule. Ce sera le numérateur de la fraction souhaitée. L'essentiel - n'en faites pas trop et ne rayez pas les zéros internes entourés d'autres nombres;
2. Calculez le nombre de chiffres dans la fraction décimale d'origine après la virgule décimale. Prenez le chiffre 1 et ajoutez autant de zéros à droite que vous avez compté les caractères. Ce sera le dénominateur;
3. En fait, écrivez la fraction dont nous venons de trouver le numérateur et le dénominateur. Réduire si possible. S'il y avait une partie entière dans la fraction d'origine, nous obtenons maintenant une fraction impropre, ce qui est très pratique pour les calculs ultérieurs.

Une tâche. Convertir les décimaux en ordinaires : 0,008 ; 3.107 ; 2,25 ; 7.2008.

Nous barrons les zéros à gauche et les virgules - nous obtenons les nombres suivants (ce seront des numérateurs): 8; 3107 ; 225 ; 72008.

Dans les première et deuxième fractions après la virgule, il y a 3 décimales, dans la deuxième - 2 et dans la troisième - jusqu'à 4 décimales. On obtient les dénominateurs : 1000 ; 1000 ; 100 ; 10000.

Enfin, combinons les numérateurs et les dénominateurs en fractions ordinaires :

Comme on peut le voir dans les exemples, la fraction résultante peut très souvent être réduite. Encore une fois, je note que toute fraction décimale peut être représentée comme une fraction ordinaire. La transformation inverse n'est pas toujours possible.

Lors de l'ajout de fractions décimales, il est nécessaire de les écrire les unes sous les autres afin que les mêmes chiffres soient les uns sous les autres et que la virgule soit sous la virgule, et d'ajouter les fractions au fur et à mesure que les nombres naturels sont ajoutés. Ajoutons, par exemple, les fractions 12,7 et 3,442. La première fraction contient un chiffre après la virgule et la seconde en contient trois. Pour effectuer l'addition, nous transformons la première fraction de sorte qu'il y ait trois chiffres après la virgule : , puis

Les décimales sont soustraites de la même manière. Trouvez la différence entre les nombres 13,1 et 0,37 :

Lors de la multiplication de fractions décimales, il suffit de multiplier les nombres donnés, en ignorant les virgules (en tant que nombres naturels), puis, par conséquent, de séparer autant de chiffres avec une virgule à droite qu'il y en a après la virgule dans les deux facteurs de total.

Par exemple, multiplions 2,7 par 1,3. Nous avons . Séparez deux chiffres à droite par une virgule (la somme des chiffres des facteurs après la virgule est égale à deux). En conséquence, nous obtenons 2,7 1,3 = 3,51.

S'il y a moins de chiffres dans le produit qu'il n'est nécessaire de séparer par une virgule, alors les zéros manquants sont écrits devant, par exemple :

Envisagez de multiplier une fraction décimale par 10, 100, 1000, etc. Multiplions la fraction 12,733 par 10. Nous avons . En séparant trois chiffres à droite par une virgule, nous obtenons Mais. Moyens,

12 733 10 = 127,33. Ainsi, multiplier une fraction décimale par Yu revient à déplacer la virgule décimale d'un chiffre vers la droite.

En général, pour multiplier une fraction décimale par 10, 100, 1000, il faut déplacer la virgule de cette fraction de 1, 2, 3 chiffres vers la droite, en attribuant si nécessaire un certain nombre de zéros à la fraction de droite). Par exemple,

La division d'une fraction décimale par un nombre naturel s'effectue de la même manière que la division d'un nombre naturel par un nombre naturel, et une virgule est placée dans le quotient une fois la division de la partie entière terminée. Divisons 22,1 par 13 :

Si la partie entière du dividende moins diviseur, alors la réponse est zéro entier, par exemple :

Considérons maintenant la division d'un nombre décimal par un nombre décimal. Disons que nous devons diviser 2,576 par 1,12. Pour ce faire, dans le dividende comme dans le diviseur, on déplace la virgule vers la droite d'autant de chiffres qu'il y a après la virgule dans le diviseur (en cet exemple pour deux). En d'autres termes, nous multiplions le dividende et le diviseur par 100 - cela ne changera pas le quotient. Ensuite, il faut diviser la fraction 257,6 par le nombre naturel 112, c'est-à-dire que le problème se ramène au cas déjà considéré :

Pour diviser une fraction décimale en il est nécessaire de déplacer la virgule vers les chiffres à gauche dans cette fraction (dans ce cas, si nécessaire, le nombre requis de zéros est attribué à gauche). Par exemple, .

Pour ce qui est de nombres naturels la division n'est pas toujours faisable, ni toujours faisable pour les nombres décimaux. Divisez par exemple 2,8 par 0,09 :

Le résultat est ce qu'on appelle la fraction décimale infinie. Dans de tels cas, passez aux fractions ordinaires. Par exemple:

Il peut s'avérer que certains nombres sont écrits sous forme de fractions ordinaires, d'autres - sous forme de nombres mixtes, et d'autres - sous forme de fractions décimales. Lorsque vous effectuez des opérations sur de tels nombres, vous pouvez faire différentes choses : soit transformer des fractions décimales en fractions ordinaires et appliquer les règles d'opérations sur fractions ordinaires, ou convertir des fractions ordinaires et des nombres mixtes en nombres décimaux (si possible) et appliquer les règles d'action sur décimales.

Les fractions décimales sont les mêmes fractions ordinaires, mais dans la soi-disant notation décimale. La notation décimale est utilisée pour les fractions avec les dénominateurs 10, 100, 1000, etc. Dans ce cas, au lieu des fractions 1/10 ; 1/100 ; 1/1000 ; ... écrire 0.1 ; 0,01 ; 0,001 ;... .

Par exemple, 0,7 ( zéro virgule sept) est une fraction 7/10 ; 5.43 ( cinq virgule quarante-trois centièmes) est une fraction mixte 5 43/100 (ou, de manière équivalente, une fraction impropre 543/100).

Il peut arriver qu'il y ait un ou plusieurs zéros juste après la virgule : 1,03 est la fraction 1 3/100 ; 17,0087 est la fraction 1787/10000. Règle générale est-ce: il doit y avoir autant de zéros au dénominateur d'une fraction ordinaire qu'il y a de chiffres après la virgule dans la fraction décimale.

Un nombre décimal peut se terminer par un ou plusieurs zéros. Il s'avère que ces zéros sont "supplémentaires" - ils peuvent simplement être supprimés : 1,30 = 1,3 ; 5,4600 = 5,46 ; 3 000 = 3. Pouvez-vous comprendre pourquoi il en est ainsi ?

Les décimales apparaissent naturellement lors de la division par des nombres "ronds" - 10, 100, 1000, ... Assurez-vous de comprendre les exemples suivants :

27:10 = 27/10 = 2 7/10 = 2,7;

579:100 = 579/100 = 5 79/100 = 5,79;

33791:1000 = 33791/1000 = 33 791/1000 = 33,791;

34,9:10 = 349/10:10 = 349/100 = 3,49;

6,35:100 = 635/100:100 = 635/10000 = 0,0635.

Remarquez-vous un modèle ici? Essayez de le formuler. Que se passe-t-il si vous multipliez un nombre décimal par 10, 100, 1000 ?

Pour convertir une fraction ordinaire en nombre décimal, vous devez l'amener à une sorte de dénominateur "rond":

2/5 = 4/10 = 0,4 ; 11/20 = 55/100 = 0,55 ; 9/2 = 45/10 = 4,5 etc.

L'ajout de fractions décimales est beaucoup plus pratique que les fractions ordinaires. L'addition est effectuée de la même manière qu'avec les nombres ordinaires - en fonction des chiffres correspondants. Lors de l'ajout dans une colonne, les termes doivent être écrits de manière à ce que leurs virgules soient sur la même verticale. La virgule de somme apparaîtra également sur la même verticale. La soustraction de fractions décimales s'effectue exactement de la même manière.

Si, lors de l'addition ou de la soustraction dans l'une des fractions, le nombre de chiffres après la virgule décimale est inférieur à celui de l'autre, alors à la fin de cette fraction, le nombre requis de zéros doit être ajouté. Vous ne pouvez pas ajouter ces zéros, mais imaginez-les simplement dans votre esprit.

Lors de la multiplication de fractions décimales, elles doivent à nouveau être multipliées comme des nombres ordinaires (dans ce cas, il n'est plus nécessaire d'écrire une virgule sous une virgule). Dans le résultat obtenu, vous devez séparer par une virgule le nombre de caractères égal au nombre total de décimales dans les deux facteurs.

Lors de la division de fractions décimales, vous pouvez simultanément déplacer la virgule vers la droite du même nombre de chiffres dans le dividende et le diviseur : le quotient ne changera pas :

2,8:1,4 = 2,8/1,4 = 28/14 = 2;

4,2:0,7 = 4,2/0,7 = 42/7 = 6;

6:1,2 = 6,0/1,2 = 60/12 = 5.

Expliquez pourquoi il en est ainsi?

1. Dessinez un carré 10x10. Couleur dans une partie égale à : a) 0,02 ; b) 0,7 ; c) 0,57 ; d) 0,91 ; e) 0,135 de l'aire de tout le carré.
2. Qu'est-ce que 2,43 carrés ? Dessinez dans l'image.
3. Divisez 37 par 10 ; 795 ; quatre ; 2.3 ; 65,27 ; 0,48 et écrivez le résultat sous forme de fraction décimale. Divisez ces nombres par 100 et 1000.
4. Multipliez par 10 les nombres 4,6 ; 6,52 ; 23,095 ; 0,01999. Multipliez ces nombres par 100 et 1000.
5. Exprimez le nombre décimal sous forme de fraction et réduisez-le :
   a) 0,5 ; 0,2 ; 0,4 ; 0,6 ; 0,8 ;
   b) 0,25 ; 0,75 ; 0,05 ; 0,35 ; 0,025 ;
   c) 0,125 ; 0,375 ; 0,625 ; 0,875 ;
   d) 0,44 ; 0,26 ; 0,92 ; 0,78 ; 0,666 ; 0,848.
6. Imaginez comme une fraction mixte : 1,5 ; 3.2 ; 6,6 ; 2,25 ; 10,75 ; 4,125 ; 23.005 ; 7.0125.
7. Écrivez une fraction commune sous forme décimale :
   a) 1/2 ; 3/2 ; 7/2 ; 15/2 ; 1/5 ; 3/5 ; 4/5 ; 18/5 ;
   b) 1/4 ; 3/4 ; 5/4 ; 19/4 ; 1/20 ; 7/20 ; 49/20 ; 1/25 ; 13/25 ; 77/25 ; 1/50 ; 17/50 ; 137/50 ;
   c) 1/8 ; 3/8 ; 5/8 ; 7/8 ; 11/8 ; 125/8 ; 1/16 ; 5/16 ; 9/16 ; 23/16 ;
   d) 1/500 ; 3/250 ; 71/200 ; 9/125 ; 27/2500 ; 1999/2000.
8. Trouvez la somme : a) 7,3 + 12,8 ; b) 65,14+49,76 ; c) 3,762+12,85 ; d) 85,4+129,756; e) 1,44+2,56.
9. Considérez une unité comme la somme de deux décimales. Trouvez vingt autres façons de le faire.
10. Trouvez la différence : a) 13,4–8,7 ; b) 74.52–27.04 ; c) 49,736–43,45 ; d) 127.24–93.883 ; e) 67-52.07 ; f) 35.24–34.9975.
11. Trouvez le produit : a) 7,6 3,8 ; b) 4,8 12,5 ; c) 2,39 7,4 ; d) 3,74 9,65.

§ 31. Tâches et exemples pour toutes les actions avec des fractions décimales.

Effectuez les étapes suivantes :

767. Trouver le quotient de division :

772. Calculer:

Trouver X , si:

776. Le nombre inconnu a été multiplié par la différence entre les nombres 1 et 0,57 et dans le produit nous avons obtenu 3,44. Trouver un numéro inconnu.

777. Montant numéro inconnu et 0,9 multiplié par la différence entre 1 et 0,4 et dans le produit nous avons obtenu 2,412. Trouver un numéro inconnu.

778. Selon le schéma sur la fusion du fer dans la RSFSR (Fig. 36), créez un problème pour la solution duquel il est nécessaire d'appliquer les actions d'addition, de soustraction et de division.

779. 1) Longueur Canal de Suez 165,8 km, la longueur du canal de Panama est inférieure de 84,7 km à celle du canal de Suez et la longueur du canal mer Blanche-Baltique est de 145,9 km plus de longueur Panama. Quelle est la longueur du canal Mer Blanche-Baltique ?

2) Le métro de Moscou (en 1959) a été construit en 5 phases. La longueur de la première ligne du métro est de 11,6 km, la seconde de 14,9 km, la longueur de la troisième est de 1,1 km inférieure à la longueur de la deuxième ligne, la longueur de la quatrième ligne est de 9,6 km de plus que la troisième ligne , et la longueur de la cinquième ligne est de 11,5 km moins la quatrième. Quelle est la longueur du métro de Moscou au début de 1959 ?

780. 1) La plus grande profondeur de l'océan Atlantique est de 8,5 km, la plus grande profondeur de l'océan Pacifique est de 2,3 km de plus que la profondeur de l'océan Atlantique et la plus grande profondeur de l'océan Arctique est 2 fois inférieure à la plus grande profondeur océan Pacifique. Quelle est la plus grande profondeur de l'océan Arctique ?

2) La voiture Moskvich consomme 9 litres d'essence aux 100 km, la voiture Pobeda consomme 4,5 litres de plus que la Moskvich et la Volga 1,1 fois plus que la Pobeda. Combien d'essence une voiture Volga utilise-t-elle pour 1 km? (Arrondissez la réponse au 0,01 litre le plus proche.)

781. 1) L'élève est allé chez son grand-père pendant les vacances. En train, il a parcouru 8,5 heures et depuis la gare à cheval 1,5 heure. Au total, il a parcouru 440 km. À quelle vitesse l'élève a-t-il roulé sur le chemin de fer s'il montait à cheval à une vitesse de 10 km/h ?

2) Le kolkhozien devait se trouver en un point situé à une distance de 134,7 km de sa maison. Pendant 2,4 heures, il a voyagé en bus à une vitesse moyenne de 55 km/h, et il a marché le reste du trajet à une vitesse de 4,5 km/h. Combien de temps a-t-il marché ?

782. 1) Au cours de l'été, un gopher détruit environ 0,12 centième de pain. Les pionniers ont exterminé 1 250 spermophiles sur 37,5 hectares au printemps. Quelle quantité de pain les écoliers ont-ils économisée pour la ferme collective ? Combien de pain est économisé pour 1 ha ?

2) La ferme collective a calculé qu'en détruisant les spermophiles sur une superficie de 15 hectares de terres arables, les écoliers ont économisé 3,6 tonnes de céréales. Combien d'écureuils terrestres sont détruits en moyenne pour 1 ha de terre si un écureuil terrestre détruit 0,012 tonne de céréales pendant l'été ?

783. 1) Lors de la mouture du blé en farine, 0,1 de son poids est perdu, et lors de la cuisson, une cuisson est obtenue égale à 0,4 du poids de la farine. Quelle quantité de pain cuit sera obtenue à partir de 2,5 tonnes de blé ?

2) La ferme collective a récolté 560 tonnes de graines de tournesol. Comment huile de tournesol sera fabriqué à partir de grains récoltés, si le poids du grain est de 0,7 poids de graines de tournesol et le poids de l'huile obtenue est de 0,25 poids de grain?

784. 1) Le rendement en crème du lait est de 0,16 poids de lait et le rendement en beurre de la crème est de 0,25 poids de crème. Combien de lait (en poids) faut-il pour obtenir 1 quintal de beurre ?

2) Combien de kilogrammes de cèpes doivent être récoltés pour obtenir 1 kg de champignons séchés, s'il reste 0,5 poids lors de la préparation pour le séchage et 0,1 poids du champignon transformé lors du séchage?

785. 1) La terre attribuée à la ferme collective est utilisée comme suit : 55 % de celle-ci est occupée par des terres arables, 35 % par des prairies, et le reste de la terre d'un montant de 330,2 hectares est affecté au jardin de la ferme collective et pour les domaines des agriculteurs collectifs. Quelle est la superficie de la ferme collective?

2) La ferme collective a semé 75% de la superficie totale ensemencée en céréales, 20% en légumes et le reste en graminées fourragères. Quelle surface ensemencée avait la ferme collective si elle semait 60 hectares d'herbes fourragères ?

786. 1) Combien de centièmes de graines faudra-t-il pour semer un champ ayant la forme d'un rectangle de 875 m de long et 640 m de large, si l'on sème 1,5 centième de graines pour 1 hectare ?

2) Combien de centièmes de graines faudra-t-il pour semer un champ qui a la forme d'un rectangle si son périmètre est de 1,6 km ? La largeur du champ est de 300 m.Pour semer 1 hectare, il faut 1,5 q de graines.

787. Combien d'enregistrements forme carree de 0,2 dm de côté tiendra dans un rectangle de 0,4 dm x 10 dm ?

788. La salle de lecture a des dimensions de 9,6 m x 5 m x 4,5 m. m d'air ?

789. 1) Quelle surface de la prairie sera fauchée par un tracteur avec une remorque de quatre faucheuses en 8 heures, si la largeur de travail de chaque faucheuse est de 1,56 m et la vitesse du tracteur est de 4,5 km/h ? (Le temps des arrêts n'est pas pris en compte.) (Réponse arrondie au 0,1 ha le plus proche.)

2) La largeur de travail du semoir à légumes du tracteur est de 2,8 m. Quelle surface peut être semée avec ce semoir en 8 heures. travailler à une vitesse de 5 km/h ?

790. 1) Trouver le rendement d'une charrue de tracteur à trois corps en 10 heures. travail, si la vitesse du tracteur est de 5 km par heure, la capture d'un corps est de 35 cm et la perte de temps improductive était de 0,1 du temps total passé. (Arrondissez la réponse au 0,1 ha le plus proche.)

2) Trouver le rendement d'une charrue de tracteur à cinq sillons en 6 heures. travail, si la vitesse du tracteur est de 4,5 km par heure, la capture d'un corps est de 30 cm et la perte de temps était de 0,1 du temps total passé. (Arrondissez la réponse au 0,1 ha le plus proche.)

791. La consommation d'eau par 5 km de parcours d'une locomotive à vapeur d'un train de voyageurs est de 0,75 tonne Le réservoir d'eau du tender contient 16,5 tonnes d'eau. Combien de kilomètres le train aura-t-il assez d'eau si le réservoir était rempli à 0,9 de sa capacité ?

792. Seuls 120 wagons de fret peuvent tenir sur une voie d'évitement, avec une longueur moyenne de wagon de 7,6 m. Combien de wagons de passagers à quatre essieux, de 19,2 m de long chacun, pourront tenir sur cette voie si 24 wagons de fret supplémentaires sont placés sur cette voie ?

793. Pour la solidité du remblai ferroviaire, il est recommandé de renforcer les talus en semant herbes des champs. Pour chaque mètre carré de remblai, il faut 2,8 g de graines d'une valeur de 0,25 roubles. pour 1 kg. Combien coûtera l'ensemencement de 1,02 hectare de talus si le coût des travaux est de 0,4 du coût des semences ? (Arrondis la réponse au 1 rub le plus proche.)

794. Briqueterie amené à la gare chemin de fer briques. 25 chevaux et 10 camions travaillaient au transport des briques. Chaque cheval transportait 0,7 tonne par voyage et effectuait 4 voyages par jour. Chaque wagon transportait 2,5 tonnes par voyage et effectuait 15 voyages par jour. Le voyage a duré 4 jours. Combien de briques ont été livrées à la station si poids moyen une brique 3,75 kg ? (Arrondis la réponse au millier de pièces près.)

795. Le stock de farine a été réparti entre trois boulangeries : la première a reçu 0,4 du stock total, la seconde 0,4 du reste et la troisième boulangerie a reçu 1,6 tonne de farine de moins que la première. Quelle quantité de farine a été distribuée au total ?

796. Il y a 176 étudiants en deuxième année de l'institut, 0,875 de ce nombre en troisième année, et une fois et demie plus qu'en troisième année en première année. Le nombre d'étudiants en première, deuxième et troisième années était de 0,75 du nombre total d'étudiants de cet institut. Combien y avait-il d'étudiants à l'institut ?

___________

797. Trouvez la moyenne arithmétique :

1) deux nombres : 56,8 et 53,4 ; 705.3 et 707.5 ;

2) trois nombres : 46,5 ; 37,8 et 36 ; 0,84 ; 0,69 et 0,81 ;

3) quatre nombres : 5,48 ; 1,36 ; 3.24 et 2.04.

798. 1) Le matin la température était de 13,6°, à midi de 25,5° et le soir de 15,2°. Calculez la température moyenne de ce jour.

2) Quelle est la température moyenne de la semaine, si pendant la semaine le thermomètre indiquait : 21° ; 20,3° ; 22,2° ; 23,5° ; 21,1° ; 22,1° ; 20,8° ?

799. 1) L'équipe de l'école a désherbé 4,2 hectares de betteraves le premier jour, 3,9 hectares le deuxième jour et 4,5 hectares le troisième. Déterminez la production moyenne de la brigade par jour.

2) Établir la norme de temps pour la fabrication nouvelle partie 3 retourneurs ont été fournis. Le premier a fait la partie en 3,2 minutes, le deuxième en 3,8 minutes et le troisième en 4,1 minutes. Calculez le temps standard qui a été défini pour la fabrication de la pièce.

800. 1) La moyenne arithmétique de deux nombres est 36,4. L'un de ces nombres est 36,8. Trouve un autre.

2) La température de l'air a été mesurée trois fois par jour : le matin, le midi et le soir. Trouvez la température de l'air le matin, si à midi elle était de 28,4°C, le soir de 18,2°C, et la température moyenne de la journée est de 20,4°C.

801. 1) La voiture a parcouru 98,5 km au cours des deux premières heures et 138 km au cours des trois heures suivantes. Combien de kilomètres la voiture a-t-elle parcourus en moyenne par heure ?

2) Des essais de capture et de pesée de yearlings ont montré que sur 10 carpes 4 avaient un poids de 0,6 kg, 3 de 0,65 kg, 2 de 0,7 kg et 1 pesait 0,8 kg. Quel est le poids moyen d'une carpe d'un an ?

802. 1) À 2 litres de sirop d'une valeur de 1,05 roubles. pour 1 litre ajouté 8 litres d'eau. Combien coûte 1 litre d'eau au sirop ?

2) L'hôtesse a acheté une boîte de 0,5 litre de bortsch en conserve pour 36 kopecks. et bouillir avec 1,5 litre d'eau. Combien coûte une assiette de bortsch si son volume est de 0,5 litre ?

803. Travail de laboratoire"Mesurer la distance entre deux points",

1ère réception. Mesure avec un ruban à mesurer (ruban à mesurer). La classe est divisée en unités de trois personnes chacune. Accessoires : 5-6 jalons et 8-10 balises.

Avancement du travail : 1) les points A et B sont marqués et une ligne droite est tracée entre eux (voir tâche 178) ; 2) poser le mètre ruban le long de la ligne droite fixe et marquer à chaque fois l'extrémité du mètre ruban avec une étiquette. 2ème réception. Mesure, étapes. La classe est divisée en unités de trois personnes chacune. Chaque élève parcourt la distance de A à B en comptant le nombre de pas qu'il fait. En multipliant la longueur moyenne de votre pas par le nombre de pas résultant, trouvez la distance de A à B.

3ème réception. Mesurer à l'oeil. Chaque élève dessine main gauche avec un pouce levé (Fig. 37) et dirige pouce sur un jalon jusqu'au point B (sur la figure - un arbre) de sorte que l'œil gauche (point A), le pouce et le point B soient sur la même ligne droite. Sans changer de position, fermez l'œil gauche et regardez à droite le pouce. Le déplacement résultant est mesuré à l'œil nu et augmenté d'un facteur 10. C'est la distance de A à B.

_________________

804. 1) Selon le recensement de 1959, la population de l'URSS était de 208,8 millions d'habitants et la population rurale était de 9,2 millions de plus que la population urbaine. Combien de citadins et combien de ruraux en URSS en 1959 ?

2) Selon le recensement de 1913, la population de la Russie était de 159,2 millions d'habitants et la population urbaine était de 103,0 millions d'habitants de moins que la population rurale. Quelle était la population urbaine et rurale de la Russie en 1913 ?

805. 1) La longueur du fil est de 24,5 m. Ce fil a été coupé en deux parties de sorte que la première partie s'est avérée être 6,8 m plus longue que la seconde. Combien de mètres de long mesure chaque pièce ?

2) La somme de deux nombres est 100,05. Un nombre vaut 97,06 de plus qu'un autre. Trouvez ces chiffres.

806. 1) Il y a 8656,2 tonnes de charbon dans trois entrepôts de charbon, dans le deuxième entrepôt il y a 247,3 tonnes de charbon de plus que dans le premier, et dans le troisième c'est 50,8 tonnes de plus que dans le second. Combien y a-t-il de tonnes de charbon dans chaque entrepôt ?

2) La somme de trois nombres est 446,73. Premier numéro moins d'une seconde par 73,17 et plus que le troisième par 32,22. Trouvez ces chiffres.

807. 1) Le bateau se déplaçait le long de la rivière à une vitesse de 14,5 km/h, et à contre-courant à une vitesse de 9,5 km/h. Quelle est la vitesse du bateau en eau calme et quelle est la vitesse de la rivière ?

2) Le bateau à vapeur a parcouru 85,6 km le long du fleuve en 4 heures, et 46,2 km à contre-courant en 3 heures. Quelle est la vitesse du bateau en eau calme et quelle est la vitesse de la rivière ?

_________

808. 1) Deux navires ont livré 3 500 tonnes de fret et un navire a livré 1,5 fois plus de fret que l'autre. Quelle quantité de fret chaque navire a-t-il livré ?

2) La superficie de deux pièces est de 37,2 m². m. La superficie d'une pièce est 2 fois plus grande que l'autre. Quelle est la superficie de chaque pièce ?

809. 1) De deux localités, distantes de 32,4 km, un motocycliste et un cycliste sont partis simultanément l'un vers l'autre. Combien de kilomètres parcourront chacun d'eux avant de se rencontrer si la vitesse du motocycliste est 4 fois celle du cycliste ?

2) Trouvez deux nombres dont la somme est 26,35 et le quotient de la division d'un nombre par un autre est 7,5.

810. 1) L'usine a envoyé trois types de cargaison d'un poids total de 19,2 tonnes. Le poids du premier type de cargaison était trois fois supérieur au poids du deuxième type de cargaison et le poids du troisième type de cargaison était la moitié du poids. des premier et deuxième types de fret ensemble. Quel est le poids de chaque type de cargaison ?

2) Pendant trois mois, une équipe de mineurs a extrait 52,5 mille tonnes de minerai de fer. En mars, il a été exploité 1,3 fois, en février 1,2 fois plus qu'en janvier. Quelle quantité de minerai la brigade a-t-elle extraite chaque mois ?

811. 1) Le gazoduc Saratov-Moscou est plus long de 672 km que le canal de Moscou. Trouvez la longueur des deux structures si la longueur du gazoduc est 6,25 fois la longueur du canal de Moscou.

2) La longueur de la rivière Don est 3,934 fois la longueur de la rivière Moscou. Trouvez la longueur de chaque rivière si la longueur de la rivière Don est supérieure de 1467 km à la longueur de la rivière Moscou.

812. 1) La différence de deux nombres est de 5,2 et le quotient obtenu en divisant un nombre par un autre est de 5. Trouvez ces nombres.

2) La différence de deux nombres est de 0,96 et leur quotient est de 1,2. Trouvez ces chiffres.

813. 1) Un nombre est inférieur de 0,3 à l'autre et égal à 0,75. Trouvez ces chiffres.

2) Un nombre vaut 3,9 de plus qu'un autre nombre. Si le plus petit nombre est doublé, alors ce sera 0,5 du plus grand. Trouvez ces chiffres.

814. 1) La ferme collective a semé 2 600 hectares de terres en blé et en seigle. Combien d'hectares de terres ont été ensemencées en blé et combien en seigle, si 0,8 de la superficie ensemencée en blé est égale à 0,5 de la superficie ensemencée en seigle ?

2) La collection de deux garçons ensemble est de 660 timbres. Combien de timbres compte la collection de chaque garçon si 0,5 du nombre de timbres du premier garçon est égal à 0,6 du nombre de timbres de la collection du deuxième garçon ?

815. Deux étudiants avaient ensemble 5,4 roubles. Après que le premier ait dépensé 0,75 de son argent et le second 0,8 de son argent, il leur reste autant d'argent. De combien d'argent disposait chaque élève ?

816. 1) Deux navires partis l'un vers l'autre depuis deux ports distants de 501,9 km. Combien de temps leur faudra-t-il pour se rencontrer si la vitesse du premier vapeur est de 25,5 km/h et celle du second de 22,3 km/h ?

2) Deux trains partis l'un vers l'autre à partir de deux points distants de 382,2 km. Au bout de quelle heure se retrouveront-ils si la vitesse moyenne du premier train était de 52,8 km/h, et du second de 56,4 km/h ?

817. 1) De deux villes distantes de 462 km, deux voitures sont parties en même temps et se sont rencontrées après 3,5 heures. Trouvez la vitesse de chaque voiture si la vitesse de la première voiture était supérieure de 12 km/h à la vitesse de la deuxième voiture.

2) Des deux colonies, dont la distance est de 63 km, un motocycliste et un cycliste sont partis simultanément l'un vers l'autre et se sont rencontrés après 1,2 heure. Trouvez la vitesse du motocycliste si le cycliste roulait à une vitesse inférieure de 27,5 km/h à la vitesse du motocycliste.

818. L'étudiant a remarqué qu'un train composé d'une locomotive et de 40 wagons l'a dépassé pendant 35 secondes. Déterminez la vitesse du train par heure si la longueur de la locomotive est de 18,5 m et la longueur de la voiture est de 6,2 m. (Donnez la réponse avec une précision de 1 km par heure.)

819. 1) Un cycliste a quitté A pour B à une vitesse moyenne de 12,4 km/h. Après 3 heures 15 minutes. Un autre cycliste a laissé B vers lui à une vitesse moyenne de 10,8 km/h. Après combien d'heures et à quelle distance de A se rencontreront-ils si 0,32 la distance entre A et B est de 76 km ?

2) Depuis les villes A et B, distantes de 164,7 km, un camion de la ville A et une voiture de la ville B se sont dirigés l'un vers l'autre. La vitesse d'un camion est de 36 km et celle d'une voiture 1,25 fois plus. La voiture de tourisme est partie 1,2 heure plus tard que le camion. Au bout de combien de temps et à quelle distance de la ville B la voiture particulière rencontrera-t-elle le camion ?

820. Deux navires ont quitté le même port au même moment et se dirigent dans la même direction. Le premier paquebot parcourt 37,5 km toutes les 1,5 heures, et le second parcourt 45 km toutes les 2 heures. Combien de temps faudra-t-il pour que le premier navire soit à une distance de 10 km du second ?

821. D'un point, un piéton est parti le premier, et 1h30 après sa sortie, un cycliste est parti dans la même direction. À quelle distance du point le cycliste a-t-il rattrapé le piéton si le piéton marchait à une vitesse de 4,25 km/h, et le cycliste roulait à une vitesse de 17 km/h ?

822. Le train a quitté Moscou pour Leningrad à 6 heures. 10 minutes. le matin et marchait à une vitesse moyenne de 50 km/h. Plus tard, un avion de passagers a décollé de Moscou pour Leningrad et est arrivé à Leningrad en même temps que le train est arrivé. La vitesse moyenne de l'avion était de 325 km par heure et la distance entre Moscou et Leningrad était de 650 km. Quand l'avion a-t-il décollé de Moscou ?

823. Le bateau à vapeur est descendu pendant 5 heures, et à contre-courant pendant 3 heures et n'a parcouru que 165 km. Combien de kilomètres a-t-il parcouru en aval et combien en amont, si la vitesse du fleuve est de 2,5 km/h ?

824. Le train est parti de A et doit arriver en B à une certaine heure ; ayant parcouru la moitié du chemin et parcouru 0,8 km en 1 min., le train s'est arrêté pendant 0,25 heure; augmentant encore la vitesse de 100 m à 1 million, le train est arrivé à l'heure à B. Trouver la distance entre A et B.

825. De la ferme collective à la ville 23 km. Un facteur a fait du vélo de la ville à la ferme collective à une vitesse de 12,5 km/h. En 0,4 heure après cette IW de la ferme collective, un fermier collectif est monté dans la ville sur un cheval à une vitesse précoce de 0,6 de la vitesse du facteur. Combien de temps après son départ le kolkhozien rencontrera-t-il le facteur ?

826. Une voiture est allée de la ville A à la ville B, à 234 km de A, à une vitesse de 32 km/h. 1h75 plus tard, une deuxième voiture quitte la ville B vers la première dont la vitesse est 1,225 fois la vitesse de la première. Dans combien d'heures après son départ la deuxième voiture rencontrera-t-elle la première

827. 1) Un dactylographe peut retaper un manuscrit en 1,6 heure et un autre en 2,5 heures. Combien de temps faudra-t-il aux deux dactylographes pour retaper ce manuscrit, en travaillant ensemble ? (Arrondissez la réponse à la 0,1 heure la plus proche.)

2) La piscine est remplie de deux pompes de puissance différente. La première pompe, fonctionnant seule, peut remplir la piscine en 3,2 heures, et la seconde en 4 heures. Combien de temps faut-il pour remplir la piscine avec le fonctionnement simultané de ces pompes ? (Arrondir la réponse au 0,1 le plus proche.)

828. 1) Une équipe peut terminer une commande en 8 jours. L'autre a besoin de 0,5 fois le premier pour terminer cette commande. La troisième brigade peut terminer cette commande en 5 jours. Combien de jours l'ensemble de la commande sera-t-il complété avec un joint travail de trois brigades ? (Arrondir la réponse au 0,1 jour le plus proche.)

2) Le premier travailleur peut terminer la commande en 4 heures, le second 1,25 fois plus vite et le troisième en 5 heures. Combien d'heures faudra-t-il pour terminer une commande travail conjoint trois ouvriers ? (Arrondissez la réponse à la 0,1 heure la plus proche.)

829. Deux voitures travaillent au nettoyage des rues. Le premier d'entre eux peut nettoyer toute la rue en 40 minutes, le second nécessite 75% du temps du premier. Les deux machines ont démarré en même temps. Après un travail conjoint de 0,25 heure, la deuxième machine a cessé de fonctionner. Combien de temps après cela la première voiture a-t-elle fini de nettoyer la rue ?

830. 1) L'un des côtés du triangle mesure 2,25 cm, le second mesure 3,5 cm de plus que le premier et le troisième mesure 1,25 cm de moins que le second. Trouver le périmètre du triangle.

2) L'un des côtés du triangle mesure 4,5 cm, le second mesure 1,4 cm de moins que le premier et le troisième côté mesure la moitié de la somme des deux premiers côtés. Quel est le périmètre du triangle ?

831 . 1) La base du triangle mesure 4,5 cm et sa hauteur est inférieure de 1,5 cm. Trouver l'aire d'un triangle.

2) La hauteur du triangle est de 4,25 cm et sa base est 3 fois plus grande. Trouver l'aire d'un triangle. (Arrondir la réponse au 0,1 le plus proche.)

832. Trouvez les zones des figures ombrées (Fig. 38).

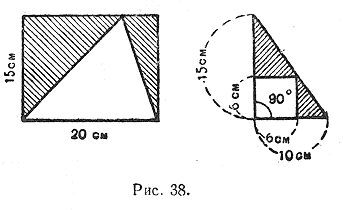
833. Quelle aire est la plus grande : un rectangle de 5 cm et 4 cm de côté, un carré de 4,5 cm de côté ou un triangle dont la base et la hauteur mesurent 6 cm chacun ?

834. La pièce a une longueur de 8,5 m, une largeur de 5,6 m et une hauteur de 2,75 m.La surface des fenêtres, des portes et des poêles est de 0,1 de la surface totale des murs de la pièce. Combien de pièces de papier peint faudra-t-il pour recouvrir cette pièce si la pièce de papier peint mesure 7 m de long et 0,75 m de large ? (Arrondissez la réponse à la pièce la plus proche.)

835. L'extérieur doit être enduit et blanchi à la chaux. Cottage, dont les dimensions sont : longueur 12 m, largeur 8 m et hauteur 4,5 m.La maison a 7 fenêtres de 0,75 m x 1,2 m chacune et 2 portes de 0,75 m x 2,5 m chacune.coût de l'ensemble des travaux, si badigeonnage et enduit 1 m² m coûte 24 kopecks.? (Arrondis la réponse au 1 rub le plus proche.)

836. Calculez la surface et le volume de votre pièce. Trouvez les dimensions de la pièce en mesurant.

837. Le jardin a la forme d'un rectangle dont la longueur est de 32 m, la largeur est de 10 m.0,05 de toute la surface du jardin est semé de carottes et le reste du jardin est planté de pommes de terre et d'oignons , et la superficie est plantée de pommes de terre 7 fois plus grandes que d'oignons. Combien de terres sont plantées individuellement avec des pommes de terre, des oignons et des carottes ?

838. Le jardin a la forme d'un rectangle dont la longueur est de 30 m et la largeur de 12 m. m plus de carottes. Combien de terres séparément sous les pommes de terre, les betteraves et les carottes ?

839. 1) Une boîte en forme de cube était gainée de tous côtés avec du contreplaqué. Quelle quantité de contreplaqué est utilisée si le bord du cube est de 8,2 dm ? (Arrondissez la réponse au 0,1 mètre carré le plus proche.)

2) Quelle quantité de peinture est nécessaire pour peindre un cube avec un bord de 28 cm, si par 1 m². cm sera dépensé 0,4 g de peinture? (Répondez, arrondissez au 0,1 kg le plus proche.)

840. La longueur de la billette en fonte, qui a la forme d'un parallélépipède rectangle, est de 24,5 cm, la largeur est de 4,2 cm et la hauteur est de 3,8 cm.Combien pèsent 200 billettes en fonte si 1 cu. la fonte dm pèse 7,8 kg ? (Arrondir la réponse au 1 kg le plus proche.)

841. 1) La longueur de la boîte (avec couvercle) ayant la forme d'un parallélépipède rectangle est de 62,4 cm, largeur 40,5 cm, hauteur 30 cm. mètres carrés de planches sont entrées dans la fabrication de la caisse, si le gaspillage de planches est de 0,2 de la surface à gainer de planches ? (Arrondissez la réponse au 0,1 m² le plus proche.)

2) Les parois inférieures et latérales de la fosse, qui a la forme d'un parallélépipède rectangle, doivent être gainées de planches. La longueur de la fosse est de 72,5 m, la largeur de 4,6 m et la hauteur de 2,2 m. Combien de mètres carrés de planches ont été utilisés pour le revêtement si le gaspillage de planches est de 0,2 de la surface à recouvrir de planches? (Arrondir la réponse au mètre carré le plus proche)

842. 1) La longueur du sous-sol, qui a la forme d'un parallélépipède rectangle, est de 20,5 m, la largeur est de 0,6 de sa longueur et la hauteur est de 3,2 m.Le sous-sol était rempli de pommes de terre de 0,8 de son volume. Combien de tonnes de pommes de terre tiennent dans le sous-sol si 1 mètre cube de pommes de terre pèse 1,5 tonne ? (Arrondir la réponse à la tonne la plus proche.)

2) La longueur du réservoir, qui a la forme d'un parallélépipède rectangle, est de 2,5 m, la largeur est de 0,4 de sa longueur et la hauteur de 1,4 m. Le réservoir est rempli de 0,6 de son volume avec du kérosène. Combien de tonnes de kérosène sont versées dans le réservoir, si le poids du kérosène dans un volume de 1 mètre cube. m est égal à 0,9 t? (Arrondir la réponse au 0,1 tonne le plus proche.)

843. 1) A quelle heure peut-on renouveler l'air dans une pièce de 8,5 m de long, 6 m de large et 3,2 m de haut, si par la fenêtre en 1 sec. passe 0,1 cu. m d'air ?

2) Calculez le temps nécessaire pour renouveler l'air de votre pièce.

844. Dimensions bloc de béton pour la construction des murs sont les suivants : 2,7 m x 1,4 m x 0,5 m Le vide représente 30 % du volume du bloc. Combien de mètres cubes de béton faudra-t-il pour fabriquer 100 blocs de ce type ?

845. Niveleuse-élévatrice (machine à creuser des fossés) en 8 heures. les travaux forment un fossé de 30 cm de large, 34 cm de profondeur et 15 km de long. Combien de pelleteuses une telle machine remplace-t-elle si une pelleteuse peut extraire 0,8 mètre cube. m par heure? (Arrondir le résultat.)

846. La poubelle en forme de parallélépipède rectangle mesure 12 mètres de long et 8 mètres de large. Dans ce casier, le grain est versé jusqu'à une hauteur de 1,5 m. Afin de savoir combien pèse le grain entier, ils ont pris une boîte de 0,5 m de long, 0,5 m de large et 0,4 m de haut, l'ont rempli de grain et l'ont pesé. Combien pesait le grain dans la cellule si le grain dans la caisse pesait 80 kg ?

849. Construire un diagramme linéaire de la croissance de la population urbaine en URSS, si en 1913 la population urbaine était de 28,1 millions de personnes, en 1926 - 24,7 millions, en 1939 - 56,1 millions et en 1959 - 99, 8 millions de personnes.

850. 1) Faites un devis pour la rénovation de votre salle de classe, si vous avez besoin de badigeonner les murs et le plafond, ainsi que de peindre le sol. Découvrez les données pour établir un devis (taille de la classe, coût du blanchiment à la chaux 1 m², coût de la peinture du sol 1 m²) auprès du responsable de l'approvisionnement de l'école.

2) Pour planter dans le jardin, l'école a acheté des plants : 30 pommiers à 0,65 roubles. par pièce, 50 cerises pour 0,4 roubles. par pièce, 40 buissons de groseilles pour 0,2 roubles. et 100 framboisiers pour 0,03 roubles. pour un buisson Rédigez une facture pour cet achat selon le modèle :

RÉPONSES

Cet article est à propos de décimales. Nous traiterons ici de la notation décimale nombres fractionnaires, nous introduisons le concept de fraction décimale et donnons des exemples de fractions décimales. Parlons ensuite des chiffres des fractions décimales, donnons les noms des chiffres. Après cela, nous nous concentrerons sur les fractions décimales infinies, disons sur les fractions périodiques et non périodiques. Ensuite, nous listons les principales actions avec des fractions décimales. En conclusion, nous établissons la position des fractions décimales sur le rayon de coordonnées.

Navigation dans les pages.

Notation décimale d'un nombre fractionnaire

Lire des nombres décimaux

Disons quelques mots sur les règles de lecture des fractions décimales.

Les fractions décimales, qui correspondent aux fractions ordinaires correctes, se lisent de la même façon que ces fractions ordinaires, seul « zéro entier » est ajouté au préalable. Par exemple, la fraction décimale 0,12 correspond à une fraction ordinaire 12/100 (elle se lit "douze centièmes"), donc 0,12 se lit comme "zéro virgule douze centièmes".

Les fractions décimales, qui correspondent à des nombres fractionnaires, se lisent exactement de la même manière que ces nombres fractionnaires. Par exemple, la décimale 56.002 correspond à nombre mixte, par conséquent, la fraction décimale 56,002 est lue comme "cinquante-six virgule deux millièmes".

Places en décimales

Dans la notation des fractions décimales, ainsi que dans la notation des nombres naturels, la valeur de chaque chiffre dépend de sa position. En effet, le chiffre 3 en décimal 0,3 signifie trois dixièmes, en décimal 0,0003 - trois dix millièmes, et en décimal 30 000,152 - trois dizaines de milliers. Ainsi, on peut parler de chiffres en décimales, ainsi que sur les chiffres des nombres naturels.

Les noms des chiffres de la fraction décimale jusqu'à la virgule coïncident complètement avec les noms des chiffres des nombres naturels. Et les noms des chiffres de la fraction décimale après la virgule sont visibles dans le tableau suivant.

Par exemple, dans la fraction décimale 37,051, le nombre 3 est à la position des dizaines, 7 à la position des unités, 0 à la dixième place, 5 à la centième place, 1 à la millième place.

Les chiffres de la fraction décimale diffèrent également par leur ancienneté. Si nous nous déplaçons de chiffre en chiffre de gauche à droite dans la notation décimale, alors nous passerons de Séniorà rangs juniors. Par exemple, le chiffre des centaines est plus ancien que le chiffre des dixièmes et le chiffre des millionièmes est plus jeune que le chiffre des centièmes. Dans cette dernière fraction décimale, on peut parler des chiffres les plus significatifs et les moins significatifs. Par exemple, en décimal 604,9387 supérieur (le plus élevé) le chiffre est le chiffre des centaines, et junior (le plus bas)- dix millième place.

Pour les fractions décimales, une expansion en chiffres a lieu. Il est similaire à l'expansion en chiffres des nombres naturels. Par exemple, le développement décimal de 45,6072 est : 45,6072=40+5+0,6+0,007+0,0002 . Et les propriétés d'addition issues du développement d'une fraction décimale en chiffres permettent d'aller vers d'autres représentations de cette fraction décimale, par exemple, 45.6072=45+0.6072 , ou 45.6072=40.6+5.007+0.0002 , ou 45.6072= 45.0072+0.6 .

Décimales finales

Jusqu'à présent, nous n'avons parlé que des fractions décimales, dans l'enregistrement desquelles il y a un nombre fini de chiffres après la virgule. Ces fractions sont appelées fractions décimales finales.

Définition.

Décimales finales- Ce sont des fractions décimales dont les enregistrements contiennent un nombre fini de caractères (chiffres).

Voici quelques exemples de décimales finales : 0,317 , 3,5 , 51,1020304958 , 230 032,45 .

Cependant, toutes les fractions communes ne peuvent pas être représentées comme une fraction décimale finie. Par exemple, la fraction 5/13 ne peut pas être remplacée par une fraction égale avec l'un des dénominateurs 10, 100, ..., par conséquent, elle ne peut pas être convertie en une fraction décimale finale. Nous en parlerons plus en détail dans la section théorique sur la conversion de fractions ordinaires en fractions décimales.

Décimales infinies : fractions périodiques et fractions non périodiques

En écrivant une fraction décimale après un point décimal, vous pouvez autoriser la possibilité d'un nombre infini de chiffres. Dans ce cas, nous en viendrons à la considération des fractions décimales dites infinies.

Définition.

Décimales sans fin- Ce sont des fractions décimales, dans l'enregistrement desquelles il y a un nombre infini de chiffres.

Il est clair que nous ne pouvons pas écrire les fractions décimales infinies dans leur intégralité, par conséquent, dans leur enregistrement, elles sont limitées à un certain nombre fini de chiffres après la virgule décimale et mettent des points de suspension indiquant une séquence de chiffres continue à l'infini. Voici quelques exemples de fractions décimales infinies : 0,143940932…, 3,1415935432…, 153,02003004005…, 2,111111111…, 69,74152152152….

Si vous regardez attentivement les deux dernières fractions décimales sans fin, alors dans la fraction 2,111111111 ... le nombre 1 se répétant à l'infini est clairement visible, et dans la fraction 69,74152152152 ..., à partir de la troisième décimale, le groupe de nombres répétitif 1, 5 et 2 est clairement visible. Ces fractions décimales infinies sont appelées périodiques.

Définition.

Décimales périodiques(ou simplement fractions périodiques) sont des fractions décimales infinies, dans lesquelles, à partir d'une certaine décimale, un chiffre ou un groupe de chiffres, appelé période fractionnaire.

Par exemple, la période de la fraction périodique 2,111111111… est le nombre 1, et la période de la fraction 69,74152152152… est un groupe de nombres comme 152.

Pour les fractions décimales périodiques infinies, une notation spéciale a été adoptée. Par souci de brièveté, nous avons convenu d'écrire la période une fois, en la mettant entre parenthèses. Par exemple, la fraction périodique 2.111111111… s'écrit 2,(1) , et la fraction périodique 69.74152152152… s'écrit 69.74(152) .

Il convient de noter que pour la même fraction décimale périodique, vous pouvez spécifier des périodes différentes. Par exemple, la décimale périodique 0,73333… peut être considérée comme une fraction 0,7(3) de période 3, ainsi qu'une fraction 0,7(33) de période 33, et ainsi de suite 0,7(333), 0,7(3333 ), ... Vous pouvez également regarder la fraction périodique 0,73333 ... comme ceci : 0,733(3) , ou comme ceci 0,73(333), etc. Ici, afin d'éviter toute ambiguïté et incohérence, on s'accorde à considérer comme période de la fraction décimale la plus courte de toutes séquences possibles chiffres répétés et commençant à la position la plus proche de la virgule décimale. Autrement dit, la période de la fraction décimale 0,73333… sera considérée comme une séquence d'un chiffre 3, et la périodicité commence à partir de la deuxième position après la virgule décimale, c'est-à-dire 0,73333…=0,7(3) . Autre exemple : la fraction périodique 4,7412121212… a une période de 12, la périodicité commence à partir du troisième chiffre après la virgule, soit 4,7412121212…=4,74(12) .

Les fractions périodiques décimales infinies sont obtenues en convertissant en fractions décimales des fractions ordinaires dont les dénominateurs contiennent des facteurs premiers autres que 2 et 5.

Ici, il convient de mentionner les fractions périodiques avec une période de 9. Voici des exemples de telles fractions : 6.43(9) , 27,(9) . Ces fractions sont une autre notation pour les fractions périodiques de période 0, et il est d'usage de les remplacer par des fractions périodiques de période 0. Pour ce faire, la période 9 est remplacée par la période 0 et la valeur du chiffre supérieur suivant est augmentée de un. Par exemple, une fraction de période 9 de la forme 7.24(9) est remplacée par une fraction périodique de période 0 de la forme 7.25(0) ou une fraction décimale finale égale à 7.25. Autre exemple : 4,(9)=5,(0)=5 . L'égalité d'une fraction de période 9 et de sa fraction correspondante de période 0 s'établit facilement après avoir remplacé ces fractions décimales par leurs fractions ordinaires égales.

Enfin, examinons de plus près les nombres décimaux infinis, qui n'ont pas de séquence de chiffres se répétant à l'infini. Ils sont dits non périodiques.

Définition.

Décimales non récurrentes(ou simplement fractions non périodiques) sont des nombres décimaux infinis sans période.

Parfois, les fractions non périodiques ont une forme similaire à celle des fractions périodiques, par exemple, 8,02002000200002 ... est une fraction non périodique. Dans ces cas, vous devez être particulièrement attentif à remarquer la différence.

Notez que les fractions non périodiques ne sont pas converties en fractions ordinaires, les fractions décimales non périodiques infinies représentent des nombres irrationnels.

Opérations avec des décimaux

L'une des opérations avec les décimales est la comparaison, et quatre arithmétiques de base sont également définies opérations avec des nombres décimaux: addition, soustraction, multiplication et division. Considérez séparément chacune des actions avec des fractions décimales.

Comparaison décimale repose essentiellement sur la comparaison des fractions ordinaires correspondant aux fractions décimales comparées. Cependant, la conversion de fractions décimales en fractions ordinaires est une opération plutôt laborieuse, et les fractions non répétitives infinies ne peuvent pas être représentées comme une fraction ordinaire, il est donc pratique d'utiliser une comparaison au niveau du bit des fractions décimales. La comparaison au niveau du bit des nombres décimaux est similaire à la comparaison des nombres naturels. Pour des informations plus détaillées, nous vous recommandons d'étudier l'article comparaison matérielle des fractions décimales, règles, exemples, solutions.

Passons à l'étape suivante - multiplier des nombres décimaux. La multiplication des fractions décimales finales est effectuée de la même manière que la soustraction des fractions décimales, des règles, des exemples, des solutions à la multiplication par une colonne de nombres naturels. Dans le cas de fractions périodiques, la multiplication peut se réduire à la multiplication de fractions ordinaires. À son tour, la multiplication de fractions décimales non périodiques infinies après leur arrondi est réduite à la multiplication de fractions décimales finies. Nous recommandons une étude plus approfondie du matériel de l'article multiplication des fractions décimales, règles, exemples, solutions.

Décimales sur le faisceau de coordonnées

Il existe une correspondance un à un entre les points et les décimales.

Voyons comment les points sont construits sur le rayon de coordonnées correspondant à une fraction décimale donnée.

Nous pouvons remplacer les fractions décimales finies et les fractions décimales périodiques infinies par des fractions ordinaires qui leur sont égales, puis construire les fractions ordinaires correspondantes sur le rayon de coordonnées. Par exemple, une fraction décimale 1,4 correspond à une fraction ordinaire 14/10, par conséquent, le point de coordonnée 1,4 est éloigné de l'origine dans le sens positif de 14 segments égaux à un dixième d'un seul segment.

Les fractions décimales peuvent être marquées sur le faisceau de coordonnées, à partir de l'expansion de cette fraction décimale en chiffres. Par exemple, disons que nous devons construire un point avec la coordonnée 16.3007 , puisque 16.3007=16+0.3+0.0007 , puis dans point donné peut être atteint en écartant successivement 16 segments unitaires à partir de l'origine, 3 segments dont la longueur est égale à un dixième de segment unitaire et 7 segments dont la longueur est égale à une dix millième fraction d'un seul segment.

Cette manière de construire Nombres décimaux sur le rayon de coordonnées permet de s'approcher au plus près du point correspondant à une fraction décimale infinie.

Il est parfois possible de tracer avec précision un point correspondant à une décimale infinie. Par exemple, , alors cette fraction décimale infinie 1,41421... correspond au point du rayon de coordonnées, éloigné de l'origine de la longueur de la diagonale d'un carré de côté 1 segment unité.

Le processus inverse d'obtention d'une fraction décimale correspondant à un point donné sur le faisceau de coordonnées est le soi-disant mesure décimale d'un segment. Voyons comment c'est fait.

Que notre tâche soit d'aller de l'origine à un point donné sur la ligne de coordonnées (ou de s'en approcher à l'infini s'il est impossible de s'y rendre). Avec une mesure décimale d'un segment, nous pouvons différer séquentiellement n'importe quel nombre de segments unitaires de l'origine, puis des segments dont la longueur est égale à un dixième d'un seul segment, puis des segments dont la longueur est égale à un centième d'un seul segment, etc. . En notant le nombre de segments tracés de chaque longueur, on obtient la fraction décimale correspondant à un point donné sur le rayon de coordonnées.

Par exemple, pour arriver au point M dans la figure ci-dessus, vous devez mettre de côté 1 segment d'unité et 4 segments, dont la longueur est égale au dixième de l'unité. Ainsi, le point M correspond à la fraction décimale 1,4.

Il est clair que les points du faisceau de coordonnées, qui ne peuvent être atteints lors de la mesure décimale, correspondent à des fractions décimales infinies.

Bibliographie.

• Mathématiques: études. pour 5 cellules. enseignement général institutions / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartburd. - 21e éd., effacé. - M. : Mnemosyne, 2007. - 280 p. : ill. ISBN 5-346-00699-0.
• Mathématiques. 6e année: manuel. pour l'enseignement général établissements / [N. Ya. Vilenkin et autres]. - 22e éd., Rév. - M. : Mnemosyne, 2008. - 288 p. : ill. ISBN 978-5-346-00897-2.
• Algèbre: cahier de texte pour 8 cellules. enseignement général institutions / [Yu. N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Suvorova]; éd. S.A. Telyakovsky. - 16e éd. - M. : Éducation, 2008. - 271 p. : malade. - ISBN 978-5-09-019243-9.
• Gusev V.A., Mordkovich A.G. Mathématiques (un manuel pour les candidats aux écoles techniques): Proc. indemnité.- M.; Plus haut scolaire, 1984.-351 p., ill.