Trouvez les valeurs propres de la matrice en ligne. Valeurs propres et vecteurs propres d'un opérateur linéaire

Valeurs propres(nombres) et vecteurs propres.
Exemples de solutions

Soistoimême

Des deux équations, il s'ensuit que .

Posons alors : .

Par conséquent: est le deuxième vecteur propre.

Répétons les points importants solutions:

– le système résultant a certainement décision commune(les équations sont linéairement dépendantes) ;

- "Y" est sélectionné de telle sorte qu'il soit entier et que la première coordonnée "X" soit entière, positive et aussi petite que possible.

– on vérifie que la solution particulière satisfait chaque équation du système.

Réponse .

Les "points de contrôle" intermédiaires étaient tout à fait suffisants, donc vérifier les égalités, en principe, est superflu.

À différentes sources information, les coordonnées des vecteurs propres sont assez souvent écrites non pas en colonnes, mais en lignes, par exemple : (et, pour être honnête, je les écrivais moi-même en lignes). Cette option est acceptable, mais à la lumière du sujet transformations linéaires techniquement plus pratique à utiliser vecteurs de colonne.

Peut-être que la solution vous a semblé très longue, mais c'est uniquement parce que j'ai commenté le premier exemple de manière très détaillée.

Exemple 2

matrices

On s'entraîne tout seul ! Échantillon Échantillon finition devoirs à la fin de la leçon.

Parfois, vous devez effectuer une tâche supplémentaire, à savoir :

écrire la décomposition canonique de la matrice

Ce que c'est?

Si les vecteurs propres de la matrice forment base, alors il peut être représenté par :

Où est une matrice composée des coordonnées des vecteurs propres, – diagonale matrice avec les valeurs propres correspondantes.

Cette décomposition matricielle est appelée canonique ou diagonale.

Considérons la matrice du premier exemple. Ses propres vecteurs linéairement indépendant(non colinéaire) et forment une base. Faisons une matrice à partir de leurs coordonnées :

Sur le diagonale principale matrices dans l'ordre les valeurs propres sont localisées et les éléments restants sont égaux à zéro:
- encore une fois j'insiste sur l'importance de l'ordre : "deux" correspond au 1er vecteur et se situe donc dans la 1ère colonne, "trois" - au 2ème vecteur.

Selon l'algorithme habituel pour trouver matrice inverse ou Méthode de Gauss-Jordan trouver . Non, ce n'est pas une faute de frappe ! - devant toi c'est rare, comme éclipse solaireévénement lorsque l'inverse correspondait à la matrice d'origine.

Il reste à écrire la décomposition canonique de la matrice :

Le système peut être résolu à l'aide de transformations élémentaires et dans les exemples suivants, nous aurons recours à cette méthode. Mais ici, la méthode « scolaire » fonctionne beaucoup plus rapidement. A partir de la 3ème équation on exprime : - substituer dans la seconde équation :

Puisque la première coordonnée est zéro, on obtient un système , de chaque équation dont il découle que .

Et encore faire attention à présence obligatoire dépendance linéaire. Si seule une solution triviale est obtenue , alors soit la valeur propre a été trouvée de manière incorrecte, soit le système a été compilé/résolu avec une erreur.

Les coordonnées compactes donnent de la valeur

Vecteur propre :

Et encore une fois, nous vérifions que la solution trouvée satisfait toutes les équations du système. Dans les paragraphes suivants et dans les tâches ultérieures, je recommande que ce souhait soit accepté comme une règle impérative.

2) Pour la valeur propre, suivant le même principe, on obtient le système suivant :

A partir de la 2ème équation du système on exprime : - substituer dans la troisième équation :

Puisque la coordonnée "zêta" est égale à zéro, on obtient un système , de chaque équation dont il découle dépendance linéaire.

Laisser

On vérifie que la solution satisfait toutes les équations du système.

Ainsi, le vecteur propre : .

3) Et enfin, le système correspond à sa propre valeur :

La deuxième équation semble la plus simple, nous l'exprimons donc à partir de celle-ci et la substituons dans les 1ère et 3ème équations :

Tout va bien - une dépendance linéaire a été révélée, que nous substituons dans l'expression :

En conséquence, "X" et "Y" ont été exprimés par "Z": . En pratique, il n'est pas nécessaire d'établir de telles relations ; dans certains cas, il est plus pratique d'exprimer à la fois par ou et par . Ou même un "train" - par exemple, "X" à "Y" et "Y" à "Z"

Posons alors :

On vérifie que la solution trouvée satisfait chaque équation du système et écris le troisième vecteur propre

Réponse: vecteurs propres :

Géométriquement, ces vecteurs définissent trois directions spatiales différentes ("Et retour à nouveau"), selon lequel transformation linéaire transforme les vecteurs non nuls (vecteurs propres) en vecteurs colinéaires à eux.

Si par condition il fallait trouver un développement canonique de , alors c'est possible ici, car différentes valeurs propres correspondent à différents vecteurs propres linéairement indépendants. On fait une matrice à partir de leurs coordonnées, la matrice diagonale de pertinent valeurs propres et trouver matrice inverse .

Si, selon la condition, il est nécessaire d'écrire matrice de transformation linéaire dans la base des vecteurs propres, puis nous donnons la réponse sous la forme . Il y a une différence, et une différence significative ! Car cette matrice est la matrice "de".

Un problème avec des calculs plus simples pour décision indépendante:

Exemple 5

Trouver les vecteurs propres de la transformation linéaire donnée par la matrice

Lorsque vous trouvez vos propres nombres, essayez de ne pas ramener le cas à un polynôme du 3e degré. De plus, vos solutions système peuvent différer de mes solutions - il n'y a pas d'ambiguïté ici ; et les vecteurs que vous trouvez peuvent différer des vecteurs échantillons jusqu'à la proportionnalité de leurs coordonnées respectives. Par exemple, et . Il est plus esthétique de présenter la réponse sous la forme de , mais ce n'est pas grave si vous vous arrêtez à la deuxième option. Cependant, il y a des limites raisonnables à tout, la version n'a plus l'air très bonne.

Un échantillon final approximatif du devoir à la fin de la leçon.

Comment résoudre le problème en cas de valeurs propres multiples ?

L'algorithme général reste le même, mais il a ses propres particularités, et il est conseillé de conserver certaines parties de la solution dans un style académique plus rigoureux :

Exemple 6

Trouver les valeurs propres et les vecteurs propres

La solution

Bien sûr, capitalisons la fabuleuse première colonne :

Et, après factorisation du trinôme carré :

En conséquence, des valeurs propres sont obtenues, dont deux sont des multiples.

Trouvons les vecteurs propres :

1) Nous traiterons un soldat isolé selon un schéma « simplifié » :

A partir des deux dernières équations, l'égalité est clairement visible, ce qui, évidemment, devrait être substitué dans la 1ère équation du système :

La meilleure combinaison introuvable :
Vecteur propre :

2-3) Maintenant, nous supprimons quelques sentinelles. À ce cas il pourrait s'avérer soit deux soit un vecteur propre. Quelle que soit la multiplicité des racines, on substitue la valeur dans le déterminant , ce qui nous apporte ce qui suit système homogène d'équations linéaires:

Les vecteurs propres sont exactement les vecteurs
système de décision fondamental

En fait, tout au long de la leçon, nous nous sommes uniquement occupés de trouver les vecteurs du système fondamental. Juste pour le moment ce terme n'était pas particulièrement nécessaire. Au fait, ces étudiants adroits qui, en tenue de camouflage équations homogènes, sera obligé de le fumer maintenant.

La seule action consistait à supprimer les lignes supplémentaires. Le résultat est une matrice "un par trois" avec une "étape" formelle au milieu.
– variable de base, – variables libres. Il y a deux variables libres, donc il y a aussi deux vecteurs du système fondamental.

Exprimons la variable de base en termes de variables libres : . Le facteur zéro devant le "x" lui permet de prendre absolument n'importe quelle valeur (ce qui est également clairement visible depuis le système d'équations).

Dans le cadre de ce problème, il est plus pratique d'écrire la solution générale non pas en ligne, mais en colonne :

Le couple correspond à un vecteur propre :
Le couple correspond à un vecteur propre :

Noter : des lecteurs avertis peuvent capter ces vecteurs oralement - juste en analysant le système , mais certaines connaissances sont nécessaires ici : il y a trois variables, rang de la matrice du système- unité signifie système de décision fondamental se compose de 3 – 1 = 2 vecteurs. Cependant, les vecteurs trouvés sont parfaitement visibles même sans cette connaissance, purement à un niveau intuitif. Dans ce cas, le troisième vecteur s'écrira encore « plus joliment » : . Cependant, je vous préviens, dans un autre exemple, il peut ne pas y avoir de sélection simple, c'est pourquoi la réservation est destinée à des personnes expérimentées. D'ailleurs, pourquoi ne pas prendre comme troisième vecteur, disons, ? Après tout, ses coordonnées satisfont également chaque équation du système, et les vecteurs sont linéairement indépendants. Cette option, en principe, est appropriée, mais "tordue", puisque "l'autre" vecteur est une combinaison linéaire de vecteurs du système fondamental.

Réponse: valeurs propres : , vecteurs propres :

Un exemple similaire pour une solution à faire soi-même :

Exemple 7

Trouver les valeurs propres et les vecteurs propres

Un échantillon approximatif de finition à la fin de la leçon.

Il convient de noter que dans les 6ème et 7ème exemples, un triplet de vecteurs propres linéairement indépendants est obtenu, et donc la matrice d'origine peut être représentée dans le développement canonique . Mais de telles framboises ne se produisent pas dans tous les cas :

Exemple 8

La solution: composer et résoudre équation caractéristique:

Nous développons le déterminant par la première colonne :

Nous effectuons des simplifications supplémentaires selon la méthode considérée, en évitant un polynôme du 3ème degré :

sont des valeurs propres.

Trouvons les vecteurs propres :

1) Il n'y a pas de difficultés avec la racine :

Ne soyez pas surpris, en plus du kit, des variables sont également utilisées - il n'y a pas de différence ici.

A partir de la 3ème équation on exprime - on substitue dans les 1ère et 2ème équations :

De ces deux équations découle :

Soit alors :

2-3) Pour plusieurs valeurs, on obtient le système .

Écrivons la matrice du système et, à l'aide de transformations élémentaires, amenons-la à une forme étagée :

Un vecteur propre d'une matrice carrée est celui qui, multiplié par une matrice donnée, donne un vecteur colinéaire. En mots simples, lorsqu'une matrice est multipliée par un vecteur propre, ce dernier reste le même, mais multiplié par un certain nombre.

Définition

Un vecteur propre est un vecteur V non nul qui, multiplié par une matrice carrée M, devient lui-même augmenté d'un certain nombre λ. En notation algébrique, cela ressemble à :

M × V = λ × V,

où λ est une valeur propre de la matrice M.

Envisager exemple numérique. Pour faciliter l'écriture, les nombres de la matrice seront séparés par un point-virgule. Disons que nous avons une matrice :

M = 0 ; quatre ;
6; 10.

Multiplions-le par un vecteur colonne :

V = -2 ;

En multipliant une matrice par un vecteur colonne, on obtient également un vecteur colonne. En langage mathématique strict, la formule pour multiplier une matrice 2 × 2 par un vecteur colonne ressemblerait à ceci :

M × V = M11 × V11 + M12 × V21 ;
M21 x V11 + M22 x V21.

M11 signifie l'élément de la matrice M, debout dans la première ligne et la première colonne, et M22 est l'élément situé dans la deuxième ligne et la deuxième colonne. Pour notre matrice, ces éléments sont M11 = 0, M12 = 4, M21 = 6, M22 10. Pour un vecteur colonne, ces valeurs sont V11 = –2, V21 = 1. Selon cette formule, on obtient ce qui suit résultat du produit d'une matrice carrée par un vecteur :

M × V = 0 × (-2) + (4) × (1) = 4 ;
6 × (-2) + 10 × (1) = -2.

Pour plus de commodité, nous écrivons le vecteur colonne dans une ligne. Ainsi, nous avons multiplié la matrice carrée par le vecteur (-2 ; 1), ce qui donne le vecteur (4 ; -2). Évidemment, c'est le même vecteur multiplié par λ = -2. Lambda dans ce cas désigne une valeur propre de la matrice.

Le vecteur propre d'une matrice est un vecteur colinéaire, c'est-à-dire un objet qui ne change pas de position dans l'espace lorsqu'il est multiplié par une matrice. Le concept de colinéarité en algèbre vectorielle est similaire au terme de parallélisme en géométrie. Dans l'interprétation géométrique, les vecteurs colinéaires sont des segments dirigés parallèles différentes longueurs. Depuis l'époque d'Euclide, nous savons qu'une seule ligne a un nombre infini de lignes parallèles, il est donc logique de supposer que chaque matrice a un nombre infini de vecteurs propres.

D'après l'exemple précédent, on peut voir que (-8 ; 4) et (16 ; -8) et (32, -16) peuvent être des vecteurs propres. Ce sont tous des vecteurs colinéaires correspondant à la valeur propre λ = -2. En multipliant la matrice d'origine par ces vecteurs, nous obtiendrons toujours un vecteur qui diffère de l'original de 2 fois. C'est pourquoi, lors de la résolution de problèmes de recherche d'un vecteur propre, il est nécessaire de ne trouver que des objets vectoriels linéairement indépendants. Le plus souvent, pour une matrice n × n, il existe un n-ième nombre de vecteurs propres. Notre calculateur est conçu pour l'analyse des matrices carrées du second ordre, donc presque toujours deux vecteurs propres seront trouvés en conséquence, sauf lorsqu'ils coïncident.

Dans l'exemple ci-dessus, nous connaissions à l'avance le vecteur propre de la matrice d'origine et déterminions visuellement le nombre lambda. Or, en pratique, tout se passe dans l'autre sens : au début il y a des valeurs propres et ensuite seulement des vecteurs propres.

Algorithme de solution

Regardons à nouveau la matrice originale M et essayons de trouver ses deux vecteurs propres. Donc la matrice ressemble à :

M = 0 ; quatre ;
6; 10.

Pour commencer, nous devons déterminer la valeur propre λ, pour laquelle nous devons calculer le déterminant de la matrice suivante :

(0 - λ); quatre ;
6 ; (10 - λ).

Cette matrice obtenu en soustrayant l'inconnue λ des éléments sur la diagonale principale. Le déterminant est déterminé par la formule standard :

detA = M11 × M21 − M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Puisque notre vecteur ne doit pas être nul, nous prenons l'équation résultante comme linéairement dépendante et assimilons notre déterminant detA à zéro.

(0 - λ) × (10 - λ) - 24 = 0

Ouvrons les parenthèses et obtenons l'équation caractéristique de la matrice :

λ 2 − 10λ − 24 = 0

C'est la norme équation quadratique, qui doit être résolu en fonction du discriminant.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

La racine du discriminant est sqrt(D) = 14, donc λ1 = -2, λ2 = 12. Maintenant, pour chaque valeur lambda, nous devons trouver un vecteur propre. Exprimons les coefficients du système pour λ = -2.

M - λ × E = 2 ; quatre ;
6; 12.

Dans cette formule, E est matrice d'identité. Sur la base de la matrice obtenue, nous composerons le système équations linéaires:

2x + 4a = 6x + 12a

où x et y sont des éléments du vecteur propre.

Collectons tous les X à gauche et tous les Y à droite. Évidemment - 4x = 8y. Divisez l'expression par - 4 et obtenez x = -2y. Nous pouvons maintenant déterminer le premier vecteur propre de la matrice en prenant n'importe quelle valeur des inconnues (rappelez-vous de l'infinité des vecteurs propres linéairement dépendants). Prenons y = 1, puis x = -2. Par conséquent, le premier vecteur propre ressemble à V1 = (–2 ; 1). Retour au début de l'article. C'est par cet objet vectoriel que nous avons multiplié la matrice pour démontrer le concept de vecteur propre.

Trouvons maintenant le vecteur propre pour λ = 12.

M - λ × E = -12 ; quatre
6; -2.

Composons le même système d'équations linéaires ;

-12x + 4y = 6x − 2y
-18x = -6a
3x=y.

Prenons maintenant x = 1, donc y = 3. Ainsi, le deuxième vecteur propre ressemble à V2 = (1; 3). Lors de la multiplication de la matrice d'origine par ce vecteur, le résultat sera toujours le même vecteur multiplié par 12. Ceci complète l'algorithme de résolution. Vous savez maintenant comment définir manuellement un vecteur propre d'une matrice.

déterminant;
trace, c'est-à-dire la somme des éléments sur la diagonale principale;
rang, c'est-à-dire quantité maximale lignes/colonnes linéairement indépendantes.

Le programme fonctionne selon l'algorithme ci-dessus, minimisant le processus de résolution. Il est important de préciser que dans le programme le lambda est désigné par la lettre "c". Prenons un exemple numérique.

Exemple de programme

Essayons de définir des vecteurs propres pour la matrice suivante :

M=5 ; 13;
4; 14.

Entrons ces valeurs dans les cellules de la calculatrice et obtenons la réponse sous la forme suivante :

Rang matriciel : 2 ;
Déterminant matriciel : 18 ;
Trace matricielle : 19 ;
Calcul du vecteur propre : c 2 − 19,00c + 18,00 (équation caractéristique) ;
Calcul du vecteur propre : 18 (première valeur lambda) ;
Calcul du vecteur propre : 1 (seconde valeur lambda) ;
Système d'équations du vecteur 1 : -13x1 + 13y1 = 4x1 − 4y1 ;
Système d'équation du vecteur 2 : 4x1 + 13y1 = 4x1 + 13y1 ;
Vecteur propre 1 : (1 ; 1 );
Vecteur propre 2 : (-3,25 ; 1).

Ainsi, nous avons obtenu deux vecteurs propres linéairement indépendants.

Conclusion

L'algèbre linéaire et la géométrie analytique sont des matières standard pour tout étudiant de première année en ingénierie. Un grand nombre de vecteurs et matrices est terrifiant, et il est facile de se tromper dans des calculs aussi fastidieux. Notre programme permettra aux étudiants de vérifier leurs calculs ou de résoudre automatiquement le problème de trouver un vecteur propre. Il existe d'autres calculatrices d'algèbre linéaire dans notre catalogue, utilisez-les dans votre étude ou votre travail.

www.site permet de trouver. Le site fait le calcul. Dans quelques secondes, le serveur émettra la bonne décision. L'équation caractéristique de la matrice sera une expression algébrique trouvée par la règle de calcul du déterminant matrices matrices, tandis que sur la diagonale principale, il y aura des différences dans les valeurs des éléments diagonaux et de la variable. Lors du calcul équation caractéristique pour matrice en ligne, chaque élément matrices sera multiplié par les autres éléments correspondants matrices. Rechercher en mode en ligne possible uniquement pour le carré matrices. Rechercher une opération équation caractéristique pour matrice en ligne revient à calculer la somme algébrique du produit des éléments matricesà la suite de la découverte du déterminant matrices, uniquement dans le but de déterminer équation caractéristique pour matrice en ligne. Cette opération occupe une place particulière dans la théorie matrices, vous permet de trouver des valeurs propres et des vecteurs à l'aide de racines . Trouver une tâche équation caractéristique pour matrice en ligne consiste à multiplier les éléments matrices suivi de la somme de ces produits sur certaine règle. www.site trouve équation caractéristique pour la matrice dimension donnée dans le mode en ligne. calcul équation caractéristique pour matrice en ligne pour une dimension donnée, c'est trouver un polynôme à coefficients numériques ou symboliques trouvé par la règle de calcul du déterminant matrices- comme la somme des produits des éléments correspondants matrices, uniquement dans le but de déterminer équation caractéristique pour matrice en ligne. Trouver un polynôme par rapport à une variable pour un carré matrices, comme définition équation caractéristique de la matrice, courant en théorie matrices. La valeur des racines du polynôme équation caractéristique pour matrice en ligne utilisé pour définir des vecteurs propres et des valeurs propres pour matrices. Cependant, si le déterminant matrices sera nul, alors équation caractéristique matricielle existera toujours, contrairement à l'inverse matrices. Afin de calculer équation caractéristique pour la matrice ou rechercher plusieurs à la fois matrices équations caractéristiques, vous devez consacrer beaucoup de temps et d'efforts, tandis que notre serveur trouvera équation caractéristique pour la matrice en ligne. Dans ce cas, la réponse en trouvant équation caractéristique pour matrice en ligne seront corrects et avec une précision suffisante, même si les chiffres lors de la recherche équation caractéristique pour matrice en ligne sera irrationnel. Sur le site www.site les entrées de caractères sont autorisées dans les éléments matrices, C'est équation caractéristique pour la matrice en ligne peut être représenté sous une forme symbolique générale lors du calcul matrice d'équation caractéristique en ligne. Il est utile de vérifier la réponse obtenue lors de la résolution du problème de recherche équation caractéristique pour matrice en ligne utiliser le site www.site. Lors de l'exécution de l'opération de calcul d'un polynôme - équation caractéristique de la matrice, il faut être attentif et extrêmement concentré pour résoudre ce problème. À son tour, notre site vous aidera à vérifier votre décision sur le sujet matrice d'équation caractéristique en ligne. Si vous n'avez pas le temps pour de longues vérifications des problèmes résolus, alors www.site sera certainement outil pratiqueà vérifier lors de la recherche et du calcul équation caractéristique pour matrice en ligne.

". La première partie contient les dispositions minimales nécessaires à la compréhension de la chimiométrie, et la deuxième partie contient les faits qu'il faut connaître pour une compréhension plus approfondie des méthodes d'analyse multivariée. La présentation est illustrée par des exemples réalisés dans le classeur Excel Matrice.xls qui accompagne ce document.

Les liens vers des exemples sont placés dans le texte sous forme d'objets Excel. Ces exemples sont de nature abstraite, ils ne sont nullement liés aux problèmes de la chimie analytique. Exemples réels l'utilisation de l'algèbre matricielle en chimiométrie est discutée dans d'autres textes consacrés à diverses applications chimiométriques.

La plupart des mesures effectuées en chimie analytique ne sont pas directes mais indirect. Cela signifie que dans l'expérience, au lieu de la valeur de l'analyte souhaité C (concentration), une autre valeur est obtenue X(signal) lié mais non égal à C, c'est-à-dire X(C) ≠ C. En règle générale, le type de dépendance X(C) n'est pas connu, mais heureusement en chimie analytique la plupart des mesures sont proportionnelles. Cela signifie que comme la concentration de C dans un fois, le signal X augmentera de la même quantité, c'est-à-dire X(un C) = un x(C). De plus, les signaux sont également additifs, de sorte que le signal d'un échantillon contenant deux substances avec des concentrations de C 1 et C 2 sera est égal à la somme signaux de chaque composant, c'est-à-dire X(C1 + C2) = X(C1)+ X(C2). La proportionnalité et l'additivité donnent ensemble linéarité. De nombreux exemples pourraient être donnés pour illustrer le principe de linéarité, mais il suffit de mentionner les deux plus exemples clairs- chromatographie et spectroscopie. La deuxième caractéristique inhérente à l'expérience en chimie analytique est à canaux multiples. Les équipements analytiques modernes mesurent simultanément les signaux de plusieurs canaux. Par exemple, l'intensité de la transmission lumineuse est mesurée pour plusieurs longueurs d'onde à la fois, c'est-à-dire spectre. Par conséquent, dans l'expérience, nous avons affaire à une variété de signaux X 1 , X 2 ,...., X n caractérisant l'ensemble des concentrations C 1 ,C 2 , ..., C m des substances présentes dans le système étudié.

Riz. 1 spectres

Ainsi, l'expérience analytique est caractérisée par la linéarité et la multidimensionnalité. Par conséquent, il est commode de considérer les données expérimentales comme des vecteurs et des matrices et de les manipuler à l'aide de l'appareil de l'algèbre matricielle. La fécondité de cette approche est illustrée par l'exemple de la , qui montre trois spectres pris pour 200 longueurs d'onde de 4000 à 4796 cm–1. La première ( X 1) et deuxième ( X 2) les spectres ont été obtenus pour des échantillons standards dans lesquels les concentrations de deux substances A et B sont connues : dans le premier échantillon [A] = 0,5, [B] = 0,1, et dans le second échantillon [A] = 0,2, [ B] = 0,6. Que dire d'un nouvel échantillon inconnu dont le spectre est indiqué X 3 ?

Considérons trois spectres expérimentaux X 1 , X 2 et X 3 comme trois vecteurs de dimension 200. En utilisant l'algèbre linéaire, on peut facilement montrer que X 3 = 0.1 X 1 +0.3 X 2 , donc le troisième échantillon ne contient évidemment que les substances A et B dans des concentrations [A] = 0,5×0,1 + 0,2×0,3 = 0,11 et [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Informations de base

1.1 Matrices

Matrice appelé tableau rectangulaire de nombres, par exemple

Riz. 2 Matrice

Les matrices sont indiquées par des lettres majuscules en gras ( UN), et leurs éléments - correspondant minuscule avec des indices, c'est-à-dire un ij . Le premier index numérote les lignes et le second numérote les colonnes. En chimiométrie, il est d'usage de désigner valeur maximum index avec la même lettre que l'index lui-même, mais en majuscule. Par conséquent, la matrice UN peut aussi s'écrire ( un ij , je = 1,..., je; j = 1,..., J). Pour l'exemple de matrice je = 4, J= 3 et un 23 = −7.5.

Paire de chiffres je et J est appelée la dimension de la matrice et est notée je× J. Un exemple de matrice en chimiométrie est un ensemble de spectres obtenus pour jeéchantillons sur J longueurs d'onde.

1.2. Les opérations les plus simples avec les matrices

Les matrices peuvent multiplier par des nombres. Dans ce cas, chaque élément est multiplié par ce nombre. Par exemple -

Riz. 3 Multiplier une matrice par un nombre

Deux matrices de même dimension peuvent être élémentaires plier et soustraire. Par exemple,

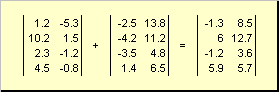
Riz. 4 Ajout de matrice

À la suite de la multiplication par un nombre et de l'addition, une matrice de même dimension est obtenue.

Une matrice nulle est une matrice composée de zéros. Il est désigné O. Il est évident que UN+O = UN, UN−UN = O et 0 UN = O.

La matrice peut transposer. Au cours de cette opération, la matrice est retournée, c'est-à-dire les lignes et les colonnes sont permutées. La transposition est indiquée par un tiret, UN" ou indice UN t. Ainsi, si UN = {un ij , je = 1,..., je; j = 1,...,J), alors UN t = ( un ji , j = 1,...,J; je = 1,..., je). Par exemple

Riz. 5 Transposition matricielle

Il est évident que ( UN t) t = UN, (UN+B) t = UN t+ B t.

1.3. Multiplication matricielle

Les matrices peuvent multiplier, mais seulement s'ils ont les dimensions appropriées. Pourquoi il en est ainsi sera clair à partir de la définition. Produit matriciel UN, dimension je× K, et matrices B, dimension K× J, est appelée la matrice C, dimension je× J, dont les éléments sont des nombres

Ainsi pour le produit UN B il faut que le nombre de colonnes dans la matrice de gauche UNétait égal au nombre de lignes dans la matrice de droite B. Exemple de produit Matrix -

Fig.6 Produit de matrices

La règle de multiplication matricielle peut être formulée comme suit. Pour trouver un élément d'une matrice C debout à l'intersection je-ième ligne et j-ième colonne ( c ij) doit être multiplié élément par élément je-ème ligne de la première matrice UN sur le j-ième colonne de la deuxième matrice B et additionnez tous les résultats. Ainsi, dans l'exemple illustré, l'élément de la troisième ligne et de la deuxième colonne est obtenu comme la somme des produits élément par élément de la troisième ligne UN et deuxième colonne B

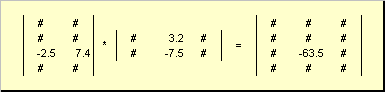
Fig.7 Élément du produit de matrices

Le produit des matrices dépend de l'ordre, c'est-à-dire UN B ≠ BA, au moins pour des raisons dimensionnelles. On dit qu'il est non commutatif. Cependant, le produit des matrices est associatif. Cela signifie que abc = (UN B)C = UN(avant JC). De plus, il est également distributif, c'est-à-dire UN(B+C) = UN B+CA. Il est évident que AO = O.

1.4. Matrices carrées

Si le nombre de colonnes d'une matrice est égal au nombre de ses lignes ( je = J=N), alors une telle matrice est appelée carré. Dans cette section, nous ne considérerons que de telles matrices. Parmi ces matrices, on peut distinguer des matrices aux propriétés particulières.

Solitaire matrice (notée je et parfois E) est une matrice dans laquelle tous les éléments sont égaux à zéro, sauf les diagonaux, qui sont égaux à 1, c'est-à-dire

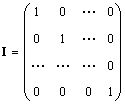
Évidemment IA = IA = UN.

La matrice s'appelle diagonale, si tous ses éléments, sauf les diagonaux ( un ii) sont égaux à zéro. Par exemple

Riz. 8 Matrice diagonale

Matrice UN appelé le sommet triangulaire, si tous ses éléments situés sous la diagonale sont égaux à zéro, c'est-à-dire un ij= 0, à je>j. Par exemple

Riz. 9 Matrice triangulaire supérieure

La matrice triangulaire inférieure est définie de manière similaire.

Matrice UN appelé symétrique, si UN t = UN. Autrement dit un ij = un ji. Par exemple

Riz. 10 Matrice symétrique

Matrice UN appelé orthogonal, si

UN t UN = AA t = je.

La matrice s'appelle Ordinaire si

1.5. Trace et déterminant

Suivant Matrice Carrée UN(noté Tr( UN) ou Sp( UN)) est la somme de ses éléments diagonaux,

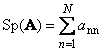
Par exemple,

Riz. 11 Trace matricielle

Il est évident que

Sp(α UN) = αSp( UN) et

Sp( UN+B) = Sp( UN)+ Sp( B).

On peut montrer que

Sp( UN) = Sp( UN t), Sp( je) = N,

et aussi que

Sp( UN B) = Sp( BA).

Une autre caractéristique importante matrice carrée est sa déterminant(noté par det( UN)). La définition du déterminant dans cas général assez compliqué, nous allons donc commencer par l'option la plus simple - la matrice UN dimensions (2×2). Alors

Pour une matrice (3×3), le déterminant sera égal à

Dans le cas d'une matrice ( N× N) le déterminant est calculé comme la somme 1 2 3 ... N= N! termes dont chacun est égal à

Indices k 1 , k 2 ,..., k N sont définis comme toutes les permutations ordonnées possibles r nombres dans l'ensemble (1, 2, ... , N). Le calcul du déterminant de la matrice est une procédure complexe qui, en pratique, est effectuée à l'aide de programmes spéciaux. Par exemple,

Riz. 12 Déterminant matriciel

Notons seulement les propriétés évidentes :

dét( je) = 1, det( UN) = det( UN t),

dét( UN B) = det( UN)det( B).

1.6. Vecteurs

Si la matrice n'a qu'une colonne ( J= 1), alors un tel objet est appelé vecteur. Plus précisément, un vecteur colonne. Par exemple

Des matrices composées d'une ligne peuvent également être envisagées, par exemple

Cet objet est aussi un vecteur, mais vecteur ligne. Lors de l'analyse des données, il est important de comprendre à quels vecteurs nous avons affaire - colonnes ou lignes. Ainsi, le spectre pris pour un échantillon peut être considéré comme un vecteur ligne. Ensuite, l'ensemble des intensités spectrales à une certaine longueur d'onde pour tous les échantillons doit être traité comme un vecteur colonne.

La dimension d'un vecteur est le nombre de ses éléments.

Il est clair que tout vecteur colonne peut être transformé en vecteur ligne par transposition, c'est-à-dire

Dans les cas où la forme d'un vecteur n'est pas spécifiquement spécifiée, mais simplement un vecteur est dit, alors ils signifient un vecteur colonne. Nous respecterons également cette règle. Un vecteur est indiqué par une lettre minuscule directe en gras. Un vecteur nul est un vecteur dont tous les éléments sont égaux à zéro. Il est noté 0 .

1.7. Les opérations les plus simples avec des vecteurs

Les vecteurs peuvent être additionnés et multipliés par des nombres de la même manière que les matrices. Par exemple,

Riz. 13 Opérations avec des vecteurs

Deux vecteurs X et y appelé colinéaire, s'il existe un nombre α tel que

1.8. Produits de vecteurs

Deux vecteurs de même dimension N peut être multiplié. Soit deux vecteurs X = (X 1 , X 2 ,...,X N)t et y = (y 1 , y 2 ,...,y NT . Guidé par la règle de multiplication "ligne par colonne", on peut en faire deux produits : X t y et xy t. Premier travail

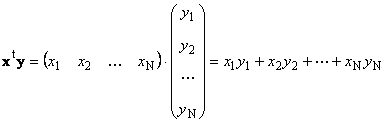
appelé scalaire ou interne. Son résultat est un nombre. Il utilise également la notation ( X,y)= X t y. Par exemple,

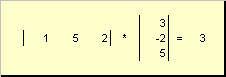
Riz. 14 Produit interne (scalaire)

Deuxième œuvre

appelé externe. Son résultat est une matrice de dimension ( N× N). Par exemple,

Riz. 15 Produit extérieur

Vecteurs, produit scalaire qui est égal à zéro sont appelés orthogonal.

1.9. Norme vectorielle

Le produit scalaire d'un vecteur avec lui-même s'appelle un carré scalaire. Cette valeur

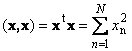
définit un carré longueur vecteur X. Pour désigner la longueur (également appelée la norme vecteur) la notation est utilisée

Par exemple,

Riz. 16 Norme vectorielle

Vecteur de longueur unitaire (|| X|| = 1) est dit normalisé. Vecteur non nul ( X ≠ 0 ) peut être normalisé en le divisant par la longueur, c'est-à-dire X = ||X|| (X/||X||) = ||X|| e. Ici e = X/||X|| est un vecteur normalisé.

Les vecteurs sont dits orthonormés s'ils sont tous normalisés et orthogonaux deux à deux.

1.10. Angle entre les vecteurs

Le produit scalaire définit et coinφ entre deux vecteurs X et y

Si les vecteurs sont orthogonaux, alors cosφ = 0 et φ = π/2, et s'ils sont colinéaires, alors cosφ = 1 et φ = 0.

1.11. Représentation vectorielle d'une matrice

Chaque matrice UN Taille je× J peut être représenté par un ensemble de vecteurs

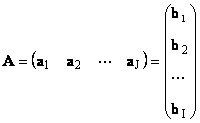
Ici chaque vecteur un j est j-ième vecteur de colonne et de ligne b je est je-ème ligne de la matrice UN

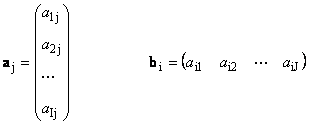
1.12. Vecteurs linéairement dépendants

Vecteurs de même dimension ( N) peut être additionné et multiplié par un nombre, tout comme les matrices. Le résultat est un vecteur de même dimension. Soit plusieurs vecteurs de même dimension X 1 , X 2 ,...,X K et le même nombre de nombres α α 1 , α 2 ,...,α K. Vecteur

y= α 1 X 1 + α 2 X 2 +...+α K X K

appelé combinaison linéaire vecteurs X k .

S'il existe de tels nombres non nuls α k ≠ 0, k = 1,..., K, Quel y = 0 , alors un tel ensemble de vecteurs X k appelé linéairement dépendant. Sinon, les vecteurs sont dits linéairement indépendants. Par exemple, les vecteurs X 1 = (2, 2) t et X 2 = (−1, −1) t sont linéairement dépendants, puisque X 1 +2X 2 = 0

1.13. Rang matriciel

Considérez un ensemble de K vecteurs X 1 , X 2 ,...,X K dimensions N. Le rang de ce système de vecteurs est le nombre maximal de vecteurs linéairement indépendants. Par exemple dans l'ensemble

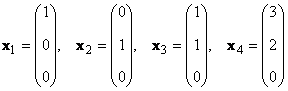
il n'y a que deux linéaires vecteur indépendant, par exemple X 1 et X 2 , donc son rang est 2.

Évidemment, s'il y a plus de vecteurs dans l'ensemble que leur dimension ( K>N), alors ils sont nécessairement linéairement dépendants.

Rang matriciel(désigné par rang( UN)) est le rang du système de vecteurs qui le compose. Bien que toute matrice puisse être représentée de deux manières (vecteurs de colonne ou vecteurs de ligne), cela n'affecte pas la valeur de rang, car

1.14. matrice inverse

Matrice Carrée UN est dit non dégénéré s'il a un unique inverse matrice UN-1 , déterminé par les conditions

AA −1 = UN −1 UN = je.

La matrice inverse n'existe pas pour toutes les matrices. Une condition nécessaire et suffisante pour la non-dégénérescence est

dét( UN) ≠ 0 ou rang( UN) = N.

L'inversion de matrice est une procédure complexe pour laquelle il existe des programmes spéciaux. Par exemple,

Riz. 17 Inversion de matrice

Nous donnons des formules pour le cas le plus simple - matrices 2 × 2

Si les matrices UN et B sont non dégénérés, alors

(UN B) −1 = B −1 UN −1 .

1.15. Matrice pseudo-inverse

Si la matrice UN est dégénéré et matrice inverse n'existe pas, dans certains cas, vous pouvez utiliser pseudo-inverse matrice, qui est définie comme une telle matrice UN+ ça

AA + UN = UN.

La matrice pseudo-inverse n'est pas la seule et sa forme dépend de la méthode de construction. Par exemple, pour une matrice rectangulaire, vous pouvez utiliser la méthode Moore-Penrose.

Si le nombre de colonnes moins que le nombre lignes, puis

UN + =(UN t UN) −1 UN t

Par exemple,

Riz. 17a Pseudo inversion de matrice

Si le nombre de colonnes est supérieur au nombre de lignes, alors

UN + =UN t ( AA t) −1

1.16. Multiplication d'un vecteur par une matrice

Vecteur X peut être multiplié par une matrice UN dimension convenable. Dans ce cas, le vecteur colonne est multiplié à droite Hache, et la chaîne vectorielle est à gauche X t UN. Si la dimension du vecteur J, et la dimension de la matrice je× J alors le résultat est un vecteur de dimension je. Par exemple,

Riz. 18 Multiplication vecteur-matrice

Si la matrice UN- carré ( je× je), puis le vecteur y = Hache a la même dimension que X. Il est évident que

UN(α 1 X 1 + α 2 X 2) = α 1 Hache 1 + α 2 Hache 2 .

Ainsi, les matrices peuvent être considérées comme transformations linéaires vecteurs. En particulier X = X, Bœuf = 0 .

2. Informations complémentaires

2.1. Systèmes d'équations linéaires

Laisser UN- taille de la matrice je× J, un b- vecteur dimension J. Considérez l'équation

Hache = b

par rapport au vecteur X, dimensions je. Il s'agit essentiellement d'un système de jeéquations linéaires avec J inconnue X 1 ,...,X J. Une solution existe si et seulement si

rang( UN) = rang( B) = R,

où B est la matrice de dimension augmentée je×( J+1) constitué de la matrice UN, rembourré d'une colonne b, B = (UN b). Sinon, les équations sont incohérentes.

Si un R = je = J, alors la solution est unique

X = UN −1 b.

Si un R < je, alors il y a beaucoup diverses solutions, qui peut être exprimé en termes de combinaison linéaire J−R vecteurs. Système équations homogènes Hache = 0 avec une matrice carrée UN (N× N) admet une solution non triviale ( X ≠ 0 ) si et seulement si det( UN) = 0. Si R= rang( UN)<N, alors il y a N−R solutions linéairement indépendantes.

2.2. Formes bilinéaires et quadratiques

Si un UN- c'est Matrice Carrée, un X et y- les vecteurs de la dimension correspondante, puis le produit scalaire de la forme X t Oui appelé bilinéaire la forme définie par la matrice UN. À X = y expression X t Hache appelé quadratique formulaire.

2.3. Matrices définies positives

Matrice Carrée UN appelé définie positive, si pour tout vecteur non nul X ≠ 0 ,

X t Hache > 0.

La négatif (X t Hache < 0), non négatif (X t Hache≥ 0) et non positif (X t Hache≤ 0) certaines matrices.

2.4. Décomposition de Cholesky

Si la matrice symétrique UN est définie positive, alors il existe une unique matrice triangulaire tu avec des éléments positifs, pour lesquels

UN = tu t tu.

Par exemple,

Riz. 19 Décomposition de Cholesky

2.5. décomposition polaire

Laisser UN est une matrice carrée non dégénérée de dimension N× N. Il existe alors une singulière polaire performance

UN = RS,

où S est une matrice symétrique non négative, et R est une matrice orthogonale. matrices S et R peut être défini explicitement :

S 2 = AA t ou S = (AA t) ½ et R = S −1 UN = (AA t) −½ UN.

Par exemple,

Riz. 20 Décomposition polaire

Si la matrice UN est dégénéré, alors la décomposition n'est pas unique - à savoir : S toujours seul, mais R il peut y en avoir beaucoup. La décomposition polaire représente une matrice UN en combinaison compression/étirement S et tournant R.

2.6. Vecteurs propres et valeurs propres

Laisser UN est une matrice carrée. Vecteur v appelé propre vecteur matrices UN, si

Un V = λ v,

où le nombre λ est appelé valeur propre matrices UN. Ainsi, la transformation effectuée par la matrice UN sur vecteur v, se réduit à un simple étirement ou compression de facteur λ. Le vecteur propre est déterminé à la multiplication près par la constante α ≠ 0, c'est-à-dire si v est un vecteur propre, alors α v est aussi un vecteur propre.

2.7. Valeurs propres

A la matrice UN, dimension ( N× N) ne peut pas être supérieur à N valeurs propres. Ils satisfont équation caractéristique

dét( UN − λ je) = 0,

étant équation algébrique N-ième commande. En particulier, pour une matrice 2 × 2, l'équation caractéristique a la forme

Par exemple,

Riz. 21 Valeurs propres

Ensemble de valeurs propres λ 1 ,..., λ N matrices UN appelé spectre UN.

Le spectre a diverses propriétés. En particulier

dét( UN) = λ 1×...×λ N, Sp( UN) = λ 1 +...+λ N.

Les valeurs propres d'une matrice arbitraire peuvent être des nombres complexes, mais si la matrice est symétrique ( UN t = UN), alors ses valeurs propres sont réelles.

2.8. Vecteurs propres

A la matrice UN, dimension ( N× N) ne peut pas être supérieur à N vecteurs propres, chacun correspondant à sa propre valeur. Pour déterminer le vecteur propre v n vous devez résoudre un système d'équations homogènes

(UN − λ n je)v n = 0 .

Il admet une solution non triviale car det( UN-λ n je) = 0.

Par exemple,