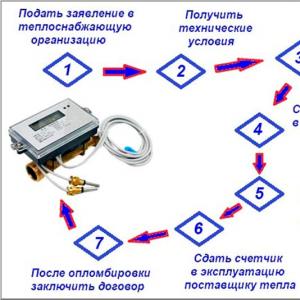
Функцийн деривативын тухай онол. e-ийн x-ийн зэрэглэлийн дериватив ба экспоненциал функц

Дериватив, түүнийг тооцоолох аргын талаар мэдлэггүйгээр математикийн физикийн бодлого, жишээг шийдвэрлэх нь туйлын боломжгүй юм. Дериватив нь хамгийн чухал ойлголтуудын нэг юм математик шинжилгээ. Бид өнөөдрийн нийтлэлийг энэ үндсэн сэдэвт зориулахаар шийдсэн. Дериватив гэж юу вэ, түүний физик, геометрийн утга нь юу вэ, функцийн деривативыг хэрхэн тооцоолох вэ? Эдгээр бүх асуултуудыг нэг дор нэгтгэж болно: деривативыг хэрхэн ойлгох вэ?

Деривативын геометрийн болон физикийн утга

Функц байх болтугай f(x) , тодорхой интервалаар өгөгдсөн (а, б) . Энэ интервалд x ба x0 цэгүүд хамаарна. X өөрчлөгдөхөд функц нь өөрөө өөрчлөгддөг. Аргументийн өөрчлөлт - түүний утгуудын ялгаа x-x0 . Энэ ялгааг дараах байдлаар бичнэ дельта х ба аргументын өсөлт гэж нэрлэдэг. Функцийн өөрчлөлт эсвэл өсөлт нь хоёр цэг дэх функцийн утгуудын зөрүү юм. Дериватив тодорхойлолт:

Тухайн цэг дэх функцийн үүсмэл утга нь өгөгдсөн цэг дэх функцийн өсөлтийг аргументийн өсөлттэй харьцуулсан харьцааны хязгаар нь тэг байх хандлагатай байдаг.

Үгүй бол дараах байдлаар бичиж болно.

Ийм хязгаар олох нь ямар учиртай юм бэ? Гэхдээ аль нь:

цэг дээрх функцийн дериватив нь OX тэнхлэг хоорондын өнцгийн тангенс ба тухайн цэг дэх функцийн графиктай шүргэгчтэй тэнцүү байна.

Деривативын физик утга: замын цаг хугацааны дериватив нь шулуун шугамын хөдөлгөөний хурдтай тэнцүү байна.

Сургуулийн наснаас эхлэн хурд бол хувийн зам гэдгийг бүгд мэддэг. x=f(t) ба цаг хугацаа т . Тодорхой хугацааны дундаж хурд:

Нэг удаад хөдөлгөөний хурдыг олж мэдэх t0 Та хязгаарыг тооцоолох хэрэгтэй:

Нэгдүгээр дүрэм: тогтмолыг гарга

Тогтмолыг деривативын тэмдгээс гаргаж авч болно. Түүнээс гадна үүнийг хийх ёстой. Математикийн жишээг шийдвэрлэхдээ дүрмээр бол - Хэрэв та илэрхийллийг хялбарчилж чадвал хялбарчлахаа мартуузай .

Жишээ. Деривативыг тооцоолъё:

Хоёрдугаар дүрэм: функцүүдийн нийлбэрийн дериватив

Хоёр функцийн нийлбэрийн дериватив нь эдгээр функцүүдийн деривативуудын нийлбэртэй тэнцүү байна. Функцийн зөрүүний деривативын хувьд ч мөн адил.

Бид энэ теоремын баталгааг өгөхгүй, харин практик жишээг авч үзэх болно.

Функцийн деривативыг ол:

Гуравдугаар дүрэм: функцүүдийн үржвэрийн дериватив

Хоёр дифференциалагдах функцийн үржвэрийн деривативыг дараах томъёогоор тооцоолно.

Жишээ нь: функцийн деривативыг ол:

Шийдэл:

Энд нарийн төвөгтэй функцүүдийн деривативын тооцооны талаар хэлэх нь чухал юм. Дериватив нарийн төвөгтэй функцнь энэ функцийн деривативын завсрын аргументыг бие даасан хувьсагчийн хувьд завсрын аргументийн деривативын үржвэртэй тэнцүү байна.

Дээрх жишээнд бид дараах илэрхийлэлтэй тулгарлаа.

AT Энэ тохиолдолдзавсрын аргумент нь тав дахь зэрэглэлд 8x байна. Ийм илэрхийллийн деривативыг тооцоолохын тулд эхлээд завсрын аргументтай холбоотой гадаад функцийн деривативыг авч үзээд дараа нь бие даасан хувьсагчийн хувьд завсрын аргументийн деривативаар үржүүлнэ.

Дөрөвдүгээр дүрэм: Хоёр функцийн хуваалтын дериватив

Хоёр функцийн категорийн деривативыг тодорхойлох томъёо:

Бид даммигийн деривативын талаар эхнээс нь ярихыг хичээсэн. Энэ сэдэв нь сонсогдож байгаа шиг тийм ч энгийн зүйл биш тул сэрэмжлүүлээрэй: жишээнүүдэд ихэвчлэн алдаа гардаг тул деривативыг тооцоолохдоо болгоомжтой байгаарай.

Энэ болон бусад сэдвээр ямар нэгэн асуулт байвал оюутны үйлчилгээтэй холбогдож болно. Пер богино хугацааБид танд хамгийн хэцүү хяналтыг шийдэж, өмнө нь деривативын тооцоолол хийж байгаагүй байсан ч гэсэн даалгавруудыг шийдвэрлэхэд тань туслах болно.

Геометр, механик, физик болон бусад мэдлэгийн салбаруудын янз бүрийн асуудлыг шийдвэрлэхдээ өгөгдсөн функцээс ижил аналитик процессыг ашиглах шаардлагатай болсон. y=f(x)гэж нэрлэгддэг шинэ функцийг авах дериватив функц(эсвэл зүгээр л f(x) функцийн дериватив)мөн бэлэгддэг

Өгөгдсөн функцийн үйл явц f(x)шинэ функц авах f"(x), дуудсан ялгахбөгөөд энэ нь дараах гурван алхмаас бүрдэнэ: 1) бид аргументыг өгнө xөсөлт  xфункцийн харгалзах өсөлтийг тодорхойлно  у = f(x+ x)-f(x); 2) харилцаа үүсгэх

3) тоолох xбайнгын, ба  x0, бид олдог
-ээр тэмдэглэгдсэн байна f"(x), үр дүнд бий болсон функц нь зөвхөн утгаас хамаарна гэдгийг онцолсон мэт x, энэ үед бид хязгаарт хүрдэг. Тодорхойлолт: Дериватив y "=f" (x) өгөгдсөн функц y=f(x) x өгөгдсөнХэрэв аргументийн өсөлт тэг байх хандлагатай байвал функцийн өсөлтийг аргументийн өсөлтөд харьцуулсан харьцааны хязгаар гэж нэрлэдэг, хэрэв мэдээжийн хэрэг, энэ хязгаар байгаа бол, өөрөөр хэлбэл. хязгаарлагдмал. Энэ замаар,
, эсвэл

Зарим үнэ цэнийн хувьд бол гэдгийг анхаарна уу x, жишээ нь хэзээ x=a, харилцаа
цагт  x0 нь хязгаарлагдмал хязгаар руу чиглэдэггүй, тэгвэл энэ тохиолдолд функц гэж хэлнэ f(x)цагт x=a(эсвэл цэг дээр x=a) нь деривативгүй эсвэл нэг цэгт ялгах боломжгүй x=a.

2. Деривативын геометрийн утга.

x 0 цэгийн ойролцоо ялгах боломжтой y \u003d f (x) функцийн графикийг авч үзье.

f(x)

Функцийн графикийн цэгийг дайран өнгөрөх дурын шугамыг авч үзье - А цэг (x 0, f (x 0)) ба графикийг B (x; f (x)) цэг дээр огтолж байна. Ийм шулуун шугамыг (AB) секант гэж нэрлэдэг. ∆ABC-аас: AC = ∆x; МЭӨ \u003d ∆y; tgβ=∆y/∆x .

АС || оноос хойш Үхэр, дараа нь ALO = BAC = β (зэрэгцээ харгалзах байдлаар). Харин ALO нь АВ секантын Ox тэнхлэгийн эерэг чиглэлд налуугийн өнцөг юм. Эндээс tgβ = k нь AB шулуун шугамын налуу юм.

Одоо бид ∆x-ийг бууруулна, өөрөөр хэлбэл. ∆x→ 0. Энэ тохиолдолд В цэг графикийн дагуу А цэгт ойртох ба АВ секант эргэлдэнэ. AB секантын ∆x → 0 дахь хязгаарын байрлал нь А цэг дээрх y \u003d f (x) функцийн графиктай шүргэгч гэж нэрлэгддэг шулуун (a) болно.

Хэрэв бид tgβ =∆y/∆x тэгшитгэлд ∆х → 0 гэж хязгаар руу шилжвэл бид дараахийг олж авна.
эсвэл tg \u003d f "(x 0), оноос хойш
-Окс тэнхлэгийн эерэг чиглэлтэй шүргэгчийн налуу өнцөг
, деривативын тодорхойлолтоор. Гэхдээ tg \u003d k нь шүргэгчийн налуу бөгөөд энэ нь k \u003d tg \u003d f "(x 0) гэсэн үг юм.

Тиймээс деривативын геометрийн утга нь дараах байдалтай байна.

х цэг дээрх функцийн дериватив 0 абсцисса х цэг дээр зурсан функцийн графиктай шүргэгчийн налуутай тэнцүү 0 .

3. Деривативын физик утга.

Шулуун шугамын дагуух цэгийн хөдөлгөөнийг авч үзье. Дурын үеийн цэгийн координатыг x(t) өгье. Мэдэгдэж байгаагаар (физикийн хичээлээс) тодорхой хугацааны дундаж хурд нь энэ хугацаанд туулсан зайг тухайн цагтай харьцуулсан харьцаатай тэнцүү байна, өөрөөр хэлбэл.

Вав = ∆x/∆t. ∆t → 0 гэж сүүлчийн тэгшитгэлийн хязгаар руу шилжье.

lim Vav (t) = (t 0) - t 0, ∆t → 0 үеийн агшин зуурын хурд.

ба lim = ∆x/∆t = x "(t 0) (деривативын тодорхойлолтоор).

Тэгэхээр (t) = x"(t) болно.

Деривативын физик утга нь дараах байдалтай байна: функцийн деривативy = е(x) цэг дээрx 0 функцийн өөрчлөлтийн хурд юме(x) цэг дээрx 0

Уг деривативыг физикт тухайн үеийн координатын мэдэгдэж буй функцээс хурдыг, цаг хугацааны хурдны мэдэгдэж буй функцээс хурдатгалыг олоход ашигладаг.

 (t) \u003d x "(t) - хурд,

a(f) = "(t) - хурдатгал, эсвэл

Хэрэв тойрог дагуух материаллаг цэгийн хөдөлгөөний хууль мэдэгдэж байгаа бол эргэлтийн хөдөлгөөний үед өнцгийн хурд ба өнцгийн хурдатгалыг олох боломжтой.

φ = φ(t) - цаг хугацааны өнцгийн өөрчлөлт,

ω \u003d φ "(t) - өнцгийн хурд,

ε = φ"(t) - өнцгийн хурдатгал, эсвэл ε = φ"(t).

Хэрэв нэгэн төрлийн бус савааны массын тархалтын хууль мэдэгдэж байгаа бол нэг төрлийн бус савааны шугаман нягтыг олж болно.

m \u003d m (x) - масс,

x  , l - бариулын урт,

p \u003d m "(x) - шугаман нягт.

Деривативын тусламжтайгаар уян хатан чанар ба гармоник чичиргээний онолын асуудлыг шийддэг. Тиймээ, Хукийн хуулийн дагуу

F = -kx, x – хувьсах координат, k – пүршний уян хатан байдлын коэффициент. ω 2 \u003d k / m-ийг тавьснаар бид хаврын дүүжин x "(t) + ω 2 x (t) \u003d 0-ийн дифференциал тэгшитгэлийг олж авна.

Энд ω = √k/√m нь хэлбэлзлийн давтамж (l/c), k нь пүршний хурд (H/m) юм.

y "+ ω 2 y \u003d 0 хэлбэрийн тэгшитгэлийг гармоник хэлбэлзлийн тэгшитгэл гэж нэрлэдэг (механик, цахилгаан, цахилгаан соронзон). Ийм тэгшитгэлийн шийдэл нь функц юм.

y = Asin(ωt + φ 0) эсвэл y = Acos(ωt + φ 0), энд

A - хэлбэлзлийн далайц, ω - мөчлөгийн давтамж,

φ 0 - эхний үе шат.

Деривативын тооцоог ихэвчлэн эндээс олдог Даалгавруудыг ашиглах. Энэ хуудасдериватив олох томъёоны жагсаалтыг агуулна.

Ялгах дүрэм

1. (k⋅f(x))′=k⋅f′(x).
2. (f(x)+g(x))′=f′(x)+g′(x).
3. (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
4. Нарийн төвөгтэй функцийн дериватив. Хэрэв y=F(u) ба u=u(x) бол y=f(x)=F(u(x)) функцийг x-ийн нийлмэл функц гэнэ. y′(x)=Fu′⋅ ux′-тай тэнцүү.
5. Далд функцийн дериватив. y=f(x) функцийг дуудна далд функц, F(x,f(x))≡0 бол F(x,y)=0 харьцаагаар өгөгдсөн.
6. Урвуу функцийн дериватив. Хэрэв g(f(x))=x бол g(x) функцийг дуудна урвуу функц y=f(x) функцийн хувьд.
7. Параметрээр өгөгдсөн функцийн дериватив. x ба у-г t хувьсагчийн функцээр өгье: x=x(t), y=y(t). Тэд y=y(x)-г параметрийн дагуу гэж хэлдэг өгөгдсөн функц x∈ (a;b) интервал дээр, хэрэв энэ интервал дээр x=x(t) тэгшитгэлийг t=t(x) болон y=y(t(x))=y(x) функцээр илэрхийлж болно. тодорхойлж болно.
8. Хүч чадлын дериватив - экспоненциал функц. Энэ нь натурал логарифмын суурь дээр логарифмыг авснаар олно.

Энэ хүснэгт дахин олон удаа хэрэг болж магадгүй тул бид танд холбоосыг хадгалахыг зөвлөж байна.

Тодорхойлолт.\(y = f(x) \) функцийг доторх \(x_0 \) цэгийг агуулсан зарим интервалд тодорхойл. Энэ интервалыг орхихгүйн тулд аргумент руу \(\Delta x \) нэмье. \(\Delta y \) (\(x_0 \) цэгээс \(x_0 + \Delta x \) цэг рүү шилжих үед) функцийн харгалзах өсөлтийг олж \(\frac(\Delta y) хамаарлыг зохио. )(\Дельта x) \). Хэрэв энэ хамаарлын хязгаар \(\Delta x \rightarrow 0 \) байгаа бол заасан хязгаарыг нэрлэнэ. дериватив функц\(y=f(x) \) цэг дээр \(x_0 \) ба \(f"(x_0) \) гэж тэмдэглэнэ.

$$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) = f"(x_0) $$

Ү тэмдгийг ихэвчлэн деривативыг илэрхийлэхэд ашигладаг. y" = f(x) гэдгийг анхаарна уу шинэ шинж тэмдэг, гэхдээ дээрх хязгаар байгаа бүх x цэгүүдэд тодорхойлогдсон y = f(x) функцтэй угаасаа холбоотой. Энэ функцийг ингэж нэрлэдэг: y = f(x) функцийн дериватив.

Деривативын геометрийн утгадараах зүйлсээс бүрдэнэ. Хэрэв у тэнхлэгтэй параллель биш шүргэгчийг y \u003d f (x) функцийн график дээр абсцисса x \u003d a цэг дээр зурж чадвал f (a) нь шүргэгчийн налууг илэрхийлнэ.
\(k = f"(a)\)

\(k = tg(a) \) тул \(f"(a) = tg(a) \) тэгшитгэл үнэн болно.

Одоо бид деривативын тодорхойлолтыг ойролцоо тэгш байдлын үүднээс тайлбарлаж байна. \(y = f(x) \) функц тодорхой \(x \) цэг дээр деривативтэй байг:
$$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) = f"(x) $$
Энэ нь x цэгийн ойролцоо ойролцоогоор \(\frac(\Delta y)(\Delta x) \prox f"(x) \), өөрөөр хэлбэл \(\Delta y \prox f"(x) \cdot гэсэн үг юм. \Дельтакс\). Олж авсан ойролцоо тэгш байдлын утга учир нь дараах байдалтай байна: функцийн өсөлт нь аргументийн өсөлттэй "бараг пропорциональ" бөгөөд пропорциональ байдлын коэффициент нь деривативын утга юм. өгсөн оноо X. Жишээлбэл, \(y = x^2 \) функцийн хувьд ойролцоогоор \(\Delta y \approx 2x \cdot \Delta x \) хүчинтэй байна. Хэрэв бид деривативын тодорхойлолтыг сайтар судалж үзвэл түүнийг олох алгоритмыг агуулсан болохыг олж мэдэх болно.

Үүнийг томъёолъё.

y \u003d f (x) функцийн деривативыг хэрхэн олох вэ?

1. \(x \) утгыг засах, \(f(x) \) олох
2. \(x \) аргументыг нэмэгдүүлэх \(\Дельта x \), шинэ цэг рүү шилжих \(x+ \Delta x \), \(f(x+ \Delta x) \) олох.
3. Функцийн өсөлтийг ол: \(\Delta y = f(x + \Delta x) - f(x) \)
4. \(\frac(\Delta y)(\Delta x) \) хамаарлыг зохио.
5. $$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) $$-г тооцоол.
Энэ хязгаар нь х дээрх функцийн дериватив юм.

Хэрэв y = f(x) функц нь x цэг дээр деривативтай бол түүнийг x цэг дээр дифференциалагдах гэж нэрлэдэг. y \u003d f (x) функцийн деривативыг олох процедурыг дуудна ялгах y = f(x) функцууд.

Дараах асуултын талаар ярилцъя: цэг дээрх функцийн тасралтгүй байдал ба дифференциал байдал хэрхэн хамааралтай вэ?

y = f(x) функцийг x цэг дээр дифференциалагдах гэж үзье. Дараа нь M (x; f (x)) цэг дээрх функцийн график руу шүргэгчийг зурж болох ба шүргэгчийн налуу нь f "(x) -тэй тэнцүү гэдгийг санаарай. Ийм график нь "эвдэж" чадахгүй. цэг M, өөрөөр хэлбэл, функц x дээр тасралтгүй байх ёстой.

Энэ нь "хуруунд" үндэслэлтэй байсан. Илүү хатуу аргументыг танилцуулъя. Хэрэв y = f(x) функц нь x цэг дээр дифференциалагдах боломжтой бол ойролцоогоор \(\Delta y \approx f"(x) \cdot \Delta x \) тэнцүү байна. тэг бол \(\Delta y \) ) нь мөн тэглэх хандлагатай байх бөгөөд энэ нь тухайн цэг дэх функцийн тасралтгүй байдлын нөхцөл юм.

Тэгэхээр, хэрэв функц нь x цэг дээр дифференциал болох юм бол тэр цэг дээр мөн тасралтгүй байна.

Эсрэг заалт нь үнэн биш юм. Жишээ нь: функц y = |x| нь хаа сайгүй, тухайлбал x = 0 цэг дээр үргэлжилдэг боловч “холбох цэг” (0; 0) дээрх функцийн графикт шүргэгч байхгүй. Хэрэв зарим үед функцийн график руу шүргэгч зурах боломжгүй бол энэ үед дериватив байхгүй болно.

Бас нэг жишээ. \(y=\sqrt(x) \) функц нь x = 0 цэгийг оруулаад бүх тооны шулуун дээр тасралтгүй байна. Мөн функцийн графикт шүргэгч нь x = 0 цэгийг оруулаад аль ч цэгт оршдог. Гэхдээ энэ үед шүргэгч нь у тэнхлэгтэй давхцаж байна, өөрөөр хэлбэл абсцисса тэнхлэгт перпендикуляр, түүний тэгшитгэл нь x \u003d 0 хэлбэртэй байна. Ийм шулуун шугамын хувьд налуу байхгүй, энэ нь \ (f) гэсэн үг юм. "(0) \) бас байхгүй

Тиймээс бид функцийн шинэ шинж чанар болох дифференциалтай танилцсан. Функц нь функцийн графикаас ялгагдах боломжтой эсэхийг яаж тодорхойлох вэ?

Хариултыг үнэндээ дээр өгөв. Хэзээ нэгэн цагт х тэнхлэгт перпендикуляр биш функцийн графикт шүргэгчийг зурж чадвал энэ үед функц дифференциал болно. Хэрэв аль нэг цэгт функцийн графикт шүргэгч байхгүй эсвэл х тэнхлэгт перпендикуляр байвал энэ үед функц ялгах боломжгүй болно.

Ялгах дүрэм

Деривативыг олох үйлдлийг гэнэ ялгах. Энэ үйлдлийг гүйцэтгэхдээ та ихэвчлэн координат, нийлбэр, функцүүдийн бүтээгдэхүүнүүд, түүнчлэн "функцуудын функцүүд", өөрөөр хэлбэл нарийн төвөгтэй функцүүдтэй ажиллах шаардлагатай болдог. Деривативын тодорхойлолт дээр үндэслэн бид энэ ажлыг хөнгөвчлөх ялгах дүрмийг гаргаж авч болно. Хэрэв C нь тогтмол тоо бөгөөд f=f(x), g=g(x) нь зарим дифференциалагдах функц байвал дараах нь үнэн болно. ялгах дүрэм:

$$ C"=0 $$ $$ x"=1 $$ $$ (f+g)"=f"+g" $$ $$ (fg)"=f"g + fg" $$ $$ ( Cf)"=Cf" $$ $$ \left(\frac(f)(g) \баруун) " = \frac(f"g-fg")(g^2) $$ $$ \left(\frac) (C)(g) \right) " = -\frac(Cg")(g^2) $$ Нийлмэл функцийн дериватив:
$$ f"_x(g(x)) = f"_g \cdot g"_x $$

Зарим функцийн деривативын хүснэгт

$$ \left(\frac(1)(x) \баруун) " = -\frac(1)(x^2) $$ $$ (\sqrt(x)) " = \frac(1)(2\ sqrt(x)) $$ $$ \left(x^a \right) " = a x^(a-1) $$ $$ \left(a^x \right) " = a^x \cdot \ln a $$ $$ \left(e^x \right) " = e^x $$ $$ (\ln x)" = \frac(1)(x) $$ $$ (\log_a x)" = \frac (1)(x\ln a) $$ $$ (\sin x)" = \cos x $$ $$ (\cos x)" = -\sin x $$ $$ (\text(tg) x) " = \frac(1)(\cos^2 x) $$ $$ (\text(ctg) x)" = -\frac(1)(\sin^2 x) $$ $$ (\arcsin x) " = \frac(1)(\sqrt(1-x^2)) $$ $$ (\arccos x)" = \frac(-1)(\sqrt(1-x^2)) $$ $$ (\text(arctg) x)" = \frac(1)(1+x^2) $$ $$ (\text(arctg) x)" = \frac(-1)(1+x^2) $ доллар

Энэ хичээлээр бид томъёо, ялгах дүрмийг хэрхэн ашиглах талаар сурах болно.

Жишээ. Функцийн деривативыг ол.

1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Дүрмийг хэрэглэх I, томьёо 4, 2 ба 1. Бид авах:

y'=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.

2. y=3x6 -2x+5. Бид ижил томъёо, томъёог ашиглан ижил төстэй байдлаар шийддэг 3.

y’=3∙6x 5 -2=18x 5 -2.

Дүрмийг хэрэглэх I, томьёо 3, 5 болон 6 болон 1.

Дүрмийг хэрэглэх IV, томьёо 5 болон 1 .

Тав дахь жишээнд дүрмийн дагуу Iнийлбэрийн дериватив нь деривативуудын нийлбэртэй тэнцүү бөгөөд бид дөнгөж сая 1-р гишүүний деривативыг олсон (жишээ нь 4 ), тиймээс бид деривативуудыг олох болно 2 дахьболон 3 дахьнөхцөл, ба 1-рнэр томъёо, бид тэр даруй үр дүнг бичиж болно.

Ялгах 2 дахьболон 3 дахьтомъёоны дагуу нэр томъёо 4 . Үүнийг хийхийн тулд бид хуваагч дахь гурав, дөрөв дэх зэрэглэлийн язгуурыг сөрөг илтгэгчтэй зэрэглэлд хөрвүүлж, дараа нь дагуу. 4 томъёогоор бид хүчнүүдийн деривативуудыг олдог.

Хараач жишээ өгсөнба үр дүн. Та загварыг барьж чадсан уу? Сайн байна. Энэ нь бид шинэ томьёотой болсон бөгөөд үүнийг деривативын хүснэгтэд нэмж болно гэсэн үг юм.

Зургаа дахь жишээг шийдэж, өөр нэг томьёо гаргая.

Бид дүрмийг ашигладаг IVболон томъёо 4 . Бид үүссэн фракцуудыг багасгадаг.

Бид энэ функц болон түүний деривативыг авч үздэг. Та мэдээжийн хэрэг загварыг ойлгож, томъёог нэрлэхэд бэлэн байна.

Шинэ томъёо сурах!

Жишээ.

1. Аргументын өсөлт ба функцийн нэмэгдлийг y= ол x2хэрэв аргументийн анхны утга байсан бол 4 , мөн шинэ 4,01 .

Шийдэл.

Шинэ аргументын утга x \u003d x 0 + Δx. Өгөгдлийг орлуулна уу: 4.01=4+Δx, улмаар аргументийн өсөлт Δх=4.01-4=0.01. Тодорхойлолтоор функцийн өсөлт нь функцийн шинэ болон өмнөх утгуудын зөрүүтэй тэнцүү байна, өөрөөр хэлбэл. Δy \u003d f (x 0 + Δx) - f (x 0). Нэгэнт бидэнд функц байгаа y=x2, дараа нь Δу\u003d (x 0 + Δx) 2 - (x 0) 2 \u003d (x 0) 2 + 2x 0 · Δx+(Δx) 2 - (x 0) 2 \u003d 2x 0 · ∆x+(∆x) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Хариулт: аргументийн өсөлт Δх=0.01; функцийн өсөлт Δу=0,0801.

Функцийн өсөлтийг өөр аргаар олох боломжтой байсан: Δy\u003d y (x 0 + Δx) -y (x 0) \u003d y (4.01) -y (4) \u003d 4.01 2 -4 2 \u003d 16.0801-16 \u003d 0.0801.

2. Функцийн графикт шүргэгчийн налуу өнцгийг ол y=f(x)цэг дээр x 0, хэрэв f "(x 0) \u003d 1.

Шийдэл.

Холбоо барих цэг дэх деривативын утга x 0ба шүргэгчийн налуугийн тангенсийн утга (үүсмэлийн геометрийн утга). Бидэнд байгаа: f "(x 0) \u003d tgα \u003d 1 → α \u003d 45 °,учир нь tg45°=1.

Хариулт: Энэ функцийн графикт шүргэгч нь Ox тэнхлэгийн эерэг чиглэлтэй тэнцүү өнцөг үүсгэнэ 45°.

3. Функцийн деривативын томъёог гарга y=xn.

Ялгаварлахфункцийн деривативыг олох үйлдэл юм.

Деривативыг олохдоо үүсмэл зэрэглэлийн томъёог гаргаж авсантай адил деривативын тодорхойлолт дээр үндэслэн гаргасан томъёог ашигладаг. (x n)" = nx n-1.

Энд томъёонууд байна.

Дериватив хүснэгтаман томъёололыг дуудах замаар цээжлэхэд хялбар байх болно:

1. Тогтмол утгын дериватив нь тэг байна.

2. X цус харвалт нэгтэй тэнцүү байна.

3. Тогтмол хүчин зүйлийг деривативын тэмдгээс гаргаж авч болно.

4. Зэрэглэлийн дериватив нь энэ зэрэглэлийн илтгэгчийн үржвэртэй ижил суурьтай градусын үржвэртэй тэнцүү боловч илтгэгч нь нэгээр бага байна.

5. Үндэсний дериватив нь ижил язгуурын хоёрт хуваагдсантай тэнцүү байна.

6. Нэгийг х-д хуваасан дериватив нь нэгийг x-д хуваасан квадрат юм.

7. Синусын дериватив нь косинустай тэнцүү байна.

8. Косинусын дериватив нь хасах синустай тэнцүү байна.

9. Шүргэгчийн дериватив нь косинусын квадратад хуваагдсантай тэнцүү байна.

10. Котангенсын дериватив нь хасах нэгийг синусын квадратад хуваасан байна.

Бид заадаг ялгах дүрэм.

1. Алгебрийн нийлбэрийн дериватив нь үүсмэл нэр томъёоны алгебрийн нийлбэртэй тэнцүү байна.

2. Бүтээгдэхүүний дериватив нь эхний хүчин зүйлийн деривативын хоёр дахь үржвэрийг нэмсэн эхний хүчин зүйлийн деривативын үржвэртэй тэнцүү байна.

3. "y"-ийн деривативыг "ve"-д хуваасан нь бутархайтай тэнцүү бөгөөд түүний хуваарьт "y" нь "ve"-ээр үржүүлсэн "y" -ийг хасах "y, цус харвалтаар үржүүлсэн", хуваарьт - "ve квадрат" гэсэн үг юм. ”.

4. онцгой тохиолдолтомъёо 3.

Хамтдаа сурцгаая!

1 хуудасны 1 1