Функцийг интервал дээр буурах гэж нэрлэдэг. Өсөх, буурах функцүүдийн хангалттай шинж тэмдэг

Монотон

Функцийн маш чухал шинж чанар нь түүний монотон байдал юм. Төрөл бүрийн тусгай функцүүдийн энэ шинж чанарыг мэдэхийн тулд янз бүрийн физик, эдийн засаг, нийгмийн болон бусад олон үйл явцын зан байдлыг тодорхойлж болно.

Хуваарилах дараах төрлүүдФункцийн монотон байдал:

1) функц нэмэгддэг, хэрэв ямар нэг интервал дээр, хэрэв аль нэг хоёр цэгийн хувьд ба энэ интервал нь . Тэдгээр. аргументийн том утга нь функцийн том утгатай тохирч байна;

2) функц буурдаг, хэрэв ямар нэг интервал дээр, хэрэв аль нэг хоёр цэгийн хувьд ба энэ интервал нь . Тэдгээр. аргументийн том утга нь функцийн бага утгатай тохирч байна;

3) функц буурдаггүй, хэрэв ямар нэг интервал дээр, хэрэв аль нэг хоёр цэгийн хувьд ба энэ интервал нь ;

4) функц нэмэгддэггүй, хэрэв ямар нэг интервал дээр, хэрэв аль нэг хоёр цэгийн хувьд ба энэ интервал нь .

2. Эхний хоёр тохиолдолд "хатуу монотон" гэсэн нэр томъёог бас ашигладаг.

3. Сүүлийн хоёр тохиолдол нь тодорхой бөгөөд ихэвчлэн хэд хэдэн функцийн бүрэлдэхүүнээр тодорхойлогддог.

4. Функцийн график дахь өсөлт, бууралтыг яг зүүнээс баруун тийш авч үзэх ёстой бөгөөд өөр юу ч биш гэдгийг бид тусад нь тэмдэглэж байна.

2. Тэгш/сондгой.

Функцийг сондгой гэж нэрлэдэг, хэрэв аргументийн тэмдэг өөрчлөгдөхөд түүний утгыг эсрэгээр өөрчилнө. Үүний томъёо нь иймэрхүү харагдаж байна . Энэ нь бүх x-ийн оронд хасах x утгыг функцэд орлуулсны дараа функц тэмдэгээ өөрчилнө гэсэн үг юм. Ийм функцийн график нь гарал үүслийн хувьд тэгш хэмтэй байна.

Хачирхалтай функцуудын жишээ гэх мэт.

Жишээлбэл, график нь гарал үүслийн хувьд үнэхээр тэгш хэмтэй байна:

Функцийг тэгш гэж нэрлэдэгхэрэв аргументийн тэмдгийг өөрчлөх нь түүний утгыг өөрчлөхгүй бол. Үүний томъёо нь иймэрхүү харагдаж байна. Энэ нь бүх x-ийн оронд хасах x утгыг функцэд орлуулсны дараа функц өөрчлөгдөхгүй гэсэн үг юм. Ийм функцийн график нь тэнхлэгт тэгш хэмтэй байна.

Тэгш функцүүдийн жишээ нь гэх мэт.

Жишээлбэл, тэнхлэгийн талаархи графикийн тэгш хэмийг харуулъя.

Хэрэв функц нь заасан төрлүүдийн аль нэгэнд хамаарахгүй бол түүнийг тэгш, сондгой ч биш, эсвэл гэж нэрлэдэг функц ерөнхий үзэл . Ийм функцууд нь тэгш хэмтэй байдаггүй.

Жишээлбэл, ийм функцийг саяхан авч үзсэн шугаман функцграфиктай:

3. тусгай өмчфункцууд юм үе үе.

Гол нь стандартад тусгагдсан үечилсэн функцууд юм сургуулийн сургалтын хөтөлбөр, нь зөвхөн тригонометрийн функцууд юм. Холбогдох сэдвийг судлахдаа бид тэдгээрийн талаар аль хэдийн дэлгэрэнгүй ярьсан.

Тогтмол функцгэдэг нь аргумент дээр тодорхой тогтмол тэгээс бусад тоог нэмэхэд утга нь өөрчлөгддөггүй функц юм.

Энэ хамгийн бага тоог дууддаг функциональ хугацаамөн үсгээр тэмдэглэгдсэн байна.

Үүний томъёо дараах байдлаар харагдаж байна. .

Энэ шинж чанарыг синусын графикийн жишээн дээр харцгаая.

Функцийн үе ба is , үе нь мөн гэдгийг санаарай.

Бид аль хэдийн мэдэж байгаа шиг, төлөө тригонометрийн функцуудхамтран нарийн төвөгтэй аргументстандарт бус хугацаа байж болно. Эдгээр нь маягтын функцууд юм:

Тэд ижил хугацаатай байдаг. Мөн функцүүдийн талаар:

Тэд ижил хугацаатай байдаг.

Таны харж байгаагаар шинэ хугацааг тооцоолохын тулд стандарт хугацааг аргумент дахь хүчин зүйлээр хуваана. Энэ нь функцийн бусад өөрчлөлтөөс хамаарахгүй.

Хязгаарлалт.

Чиг үүрэг y=f(x) Хэрэв дурын xϵX-ийн хувьд f(x) тэгш бус байдал гарах a тоо байвал X⊂D(f) олонлогийн доороос хязгаарлагдмал гэж нэрлэдэг.< a.

Чиг үүрэг y=f(x) X⊂D(f) олонлог дээр дурын xϵX-ийн хувьд f(x) тэгш бус байдал гарах тоо байгаа бол үүнийг дээрээс нь хязгаарласан гэж нэрлэдэг.< a.

Хэрэв X интервалыг заагаагүй бол функцийг бүхэл бүтэн тодорхойлолтын хүрээнд хязгаарласан гэж үзнэ. Дээр ба доор хоёуланг нь хязгаарласан функцийг хязгаарлагдмал гэж нэрлэдэг.

Функцийн хязгаарлалтыг графикаас уншихад хялбар байдаг. Ямар нэгэн шулуун y=a зурж болох ба хэрэв функц нь энэ шулуунаас өндөр байвал доороос нь хязгаарлагдана.

Хэрэв доор байгаа бол дээр дурдсан байна. Доод хязгаарлагдмал функцийн графикийг доор харуулав. Хуваарь хязгаарлагдмал функцЗалуус аа, өөрийгөө зураад үзээрэй.

Сэдэв: Функцийн шинж чанарууд: өсөлт ба бууралтын интервал; хамгийн том ба хамгийн бага утга; экстремум цэгүүд (орон нутгийн хамгийн их ба хамгийн бага), функциональ гүдгэр.

өсөлт, бууралтын үе.

Функцийн өсөлт, бууралтын хангалттай нөхцөл (тэмдэг) дээр үндэслэн функцийн өсөлт, бууралтын интервалыг олно.

Интервал дээрх функцүүдийн өсөлт ба буурах шинж тэмдгүүдийн томъёог энд оруулав.

Хэрэв функцийн дериватив бол y=f(x)аливаад эерэг xинтервалаас X, дараа нь функц нь -ээр нэмэгдэнэ X;

Хэрэв функцийн дериватив бол y=f(x)аливаад сөрөг xинтервалаас X, дараа нь функц нь буурна X.

Тиймээс функцийн өсөлт, бууралтын интервалыг тодорхойлохын тулд дараахь зүйлийг хийх шаардлагатай.

функцийн хамрах хүрээг олох;

функцийн деривативыг олох;

тэгш бус байдлыг шийдвэрлэх, тодорхойлолтын талбарт;

1. Функцийн мужийг ол

2.Функцийн деривативыг ол

3. Деривативыг тэгтэй тэнцүүлж, функцийн критик цэгүүдийг ол

4. Тодорхойлолтын талбарт чухал цэгүүдийг тэмдэглэ

5. Олж авсан интервал тус бүрт деривативын тэмдгийг тооцоол

6. Интервал бүр дэх функцийн үйлдлийг ол.

Жишээ: Функцийн өсөлт ба бууралтын интервалыг оле(x) = интервал дээрх энэ функцийн тэгийн тоо .

Шийдэл:

1.D( е) = Р

2. е"(x) =

D( е") = D( е) = Р

3. Тэгшитгэлийг шийдэж функцийн критик цэгүүдийг ол е"(x) = 0.

x(x – 10) = 0

функцийн чухал цэгүүд x= 0 ба x = 10.

4. Деривативын тэмдгийг тодорхойлъё.

е"(x) + – +

е(x) 0 10x

(-∞; 0) ба (10; +∞) интервалд функцийн дериватив эерэг ба цэгүүд дээр байна. x= 0 ба x = 10 функц е(x) нь тасралтгүй, тиймээс энэ функц нь дараах интервалууд дээр нэмэгддэг: (-∞; 0]; .

Сегментийн төгсгөлд функцийн утгуудын тэмдгийг тодорхойлъё.

е(0) = 3, е(0) > 0

е(10) = , е(10) < 0.

Сегмент дээр функц буурч, функцийн утгын тэмдэг өөрчлөгддөг тул энэ сегмент дээр функц нэг тэг байна.

Хариулт: f(x) функц нь интервалаар нэмэгдэнэ: (-∞; 0]; ;

интервал дээр функц нь функцийн нэг тэгтэй байна.

2. Функцийн экстремум цэгүүд: хамгийн их оноо ба хамгийн бага оноо. Функцийн экстремум оршин байх зайлшгүй ба хангалттай нөхцөл. Функцийг экстремумын хувьд шалгах дүрэм .

Тодорхойлолт 1:Дериватив нь тэгтэй тэнцүү байх цэгүүдийг критик буюу суурин гэж нэрлэдэг.

Тодорхойлолт 2. Хэрэв энэ цэг дэх функцийн утга нь функцийн хамгийн ойрын утгуудаас бага (илүү) байвал цэгийг функцийн хамгийн бага (хамгийн их) цэг гэж нэрлэдэг.

Хамгийн их ба доод хэмжээ гэдгийг тэмдэглэх нь зүйтэй Энэ тохиолдолдорон нутгийнх.

Зураг дээр. 1. зурагтай орон нутгийн дээд хэмжээба доод хэмжээ.

Функцийн хамгийн их ба хамгийн бага утгыг функцийн экстремум гэсэн нийтлэг нэрээр нэгтгэдэг.

Теорем 1.(функцийн экстремум байх зайлшгүй шалгуур). Хэрэв цэг дээрх дифференциал болох функц энэ цэг дээр максимум эсвэл минимумтай байвал түүний дериватив , -д алга болно.

Теорем 2.(функцийн экстремум байх хангалттай шалгуур). Хэрэв тасралтгүй функц нь эгзэгтэй цэг агуулсан зарим интервалын бүх цэгүүдэд деривативтай бол (энэ цэгээс бусад тохиолдолд) ба хэрэв аргумент эгзэгтэй цэгээр зүүнээс баруун тийш шилжихэд тэмдэг нэмэхээс хасах руу шилждэг бол энэ цэгийн функц максимумтай, тэмдэг хасахаас нэмэх рүү шилжих үед хамгийн бага утгатай байна.

Хангалттай шинж тэмдгүүдийн үндсэн дээр функцийн өсөлт, бууралтын интервалууд олддог.

Энд байгаа тэмдгүүдийн үгс:

• Хэрэв функцийн дериватив бол у = f(x)аливаад эерэг xинтервалаас X, дараа нь функц нь -ээр нэмэгдэнэ X;
• Хэрэв функцийн дериватив бол у = f(x)аливаад сөрөг xинтервалаас X, дараа нь функц нь буурна X.

Тиймээс функцийн өсөлт, бууралтын интервалыг тодорхойлохын тулд дараахь зүйлийг хийх шаардлагатай.

• функцийн хамрах хүрээг олох;

• функцийн деривативыг олох;

• Үүссэн интервалд функц тодорхойлогдсон, тасралтгүй үргэлжлэх хилийн цэгүүдийг нэмнэ.

Алгоритмыг тодруулахын тулд жишээг авч үзье.

Жишээ.

Функцийн өсөлт ба бууралтын интервалыг ол.

Шийдэл.

Эхний алхам бол функцийн тодорхойлолтын хамрах хүрээг олох явдал юм. Бидний жишээн дээр хуваагч дахь илэрхийлэл алга болохгүй, тиймээс, .

Дериватив функц руу шилжье:

Функцийн өсөлт ба бууралтын интервалыг хангалттай шалгуураар тодорхойлохын тулд тэгш бус байдлыг шийднэ. болон тодорхойлолтын домэйн дээр. Интервалын аргын ерөнхий ойлголтыг ашиглая. Тоолуурын цорын ганц жинхэнэ үндэс нь юм x=2, мөн хуваагч нь алга болно x=0. Эдгээр цэгүүд нь тодорхойлолтын мужийг функцийн дериватив тэмдэгээ хадгалах интервалд хуваадаг. Эдгээр цэгүүдийг тоон шулуун дээр тэмдэглэе. Нэмэх ба хасах зэргээр бид дериватив эерэг эсвэл сөрөг байх интервалыг нөхцөлт байдлаар тэмдэглэдэг. Доорх сумнууд нь харгалзах интервал дээрх функцийн өсөлт, бууралтыг схемээр харуулав.

Энэ замаар, болон .

Яг цэг дээр x=2Функц нь тодорхой бөгөөд тасралтгүй байдаг тул үүнийг нэмэгдүүлэх болон буурах интервалд хоёуланд нь нэмэх шаардлагатай. Яг цэг дээр x=0функц тодорхойлогдоогүй тул энэ цэгийг шаардлагатай интервалд оруулаагүй болно.

Бид олж авсан үр дүнг харьцуулахын тулд функцийн графикийг толилуулж байна.

Хариулт:функц нь нэмэгддэг , интервал дээр буурдаг (0; 2] .

- Нэг хувьсагчийн функцийн экстремум цэгүүд. Экстремум үүсэх хангалттай нөхцөл

Интервалд тодорхойлогдсон, үргэлжилсэн f(x) функц нь монотон биш байг. Дотоод цэг дээрх функцээр хамгийн их ба хамгийн бага утгуудад хүрдэг интервалын ийм хэсгүүд байдаг [ , ]. хооронд i.

Хэрэв энэ цэгийг функц өгөгдсөн интервалд агуулагдах ийм хөршөөр (x 0 - ,x 0 +) хүрээлж чадвал f(x) функц нь тухайн цэг дээр максимум (эсвэл минимум) байна гэж хэлдэг. тэгш бус байдал нь түүний бүх цэгүүдэд хангагдана.

f(x)< f(x 0)(или f(x)>f(x0))

Өөрөөр хэлбэл, f (x 0) утга нь зарим үед ( at) функцийн авсан утгуудын хамгийн том (хамгийн бага) нь болж хувирвал x 0 цэг нь f (x) функцийг хамгийн их (хамгийн бага) өгдөг. хамгийн бага) энэ цэгийн хөрш. Хамгийн их (хамгийн бага)-ийн тодорхойлолт нь функцийг x 0 цэгийн хоёр талд өгөгдсөн гэж үздэгийг анхаарна уу.

Хэрэв (x=x 0-ийн хувьд) хатуу тэгш бус байдал байх ийм хөрш байгаа бол

f(x) f(x0)

дараа нь тэд функц нь x 0 цэг дээр өөрийн максимумтай (минимум) байна гэж хэлдэг, эс тэгвээс энэ нь буруу байна.

Хэрэв функц нь x 0 ба x 1 цэгүүдэд максимумтай бол Вейерштрассын хоёр дахь теоремыг интервалд хэрэглэснээр функц нь x 0 ба x 1 хооронд ямар нэгэн x 2 цэгт энэ интервал дахь хамгийн бага утгад хүрч, тэнд хамгийн багадаа. Үүний нэгэн адил хоёр доод цэгийн хооронд өндөр байх нь гарцаагүй. Хамгийн энгийн (болон практикт хамгийн чухал) тохиолдолд функц ерөнхийдөө зөвхөн хязгаарлагдмал тооны максимум ба минимумтай бол тэдгээр нь зүгээр л ээлжлэн солигддог.

Хамгийн их эсвэл доод хэмжээг тодорхойлохын тулд тэдгээрийг нэгтгэдэг нэр томъёо байдаг - экстремум.

Хамгийн их (max f(x)) ба хамгийн бага (min f(x)) гэсэн ойлголтууд нь функцийн орон нутгийн шинж чанарууд бөгөөд тодорхой x 0 цэгт явагддаг. Хамгийн их (sup f(x)) ба хамгийн бага (inf f(x)) утгуудын ойлголтууд нь төгсгөлтэй сегментийг хэлдэг бөгөөд сегмент дээрх функцийн глобал шинж чанарууд юм.

Зураг 1-ээс харахад x 1 ба x 3 цэгүүдэд орон нутгийн максимумууд, x 2 ба x 4 цэгүүдэд орон нутгийн минимумууд байдаг. Гэсэн хэдий ч, хамгийн бага утгафункц x=a цэгт хүрч, x=b цэг дээр хамгийн ихдээ хүрнэ.

Функцийг экстремумаар хангадаг аргументийн бүх утгыг олох асуудлыг тавьцгаая. Үүнийг шийдвэрлэхэд дериватив гол үүрэг гүйцэтгэнэ.

Эхлээд (a,b) интервал дахь f(x) функцийн хувьд төгсгөлтэй дериватив байна гэж бодъё. Хэрэв x 0 цэг дээр функц нь экстремумтай байвал дээр дурдсан Ферма теоремыг (x 0 -, x 0 +) интервалд хэрэглэснээр f (x) \u003d 0 нь зайлшгүй шаардлагатай гэж дүгнэж байна. экстремумын нөхцөл. Экстремумыг зөвхөн дериватив нь тэгтэй тэнцүү байх цэгүүдээс хайх хэрэгтэй.

Гэсэн хэдий ч дериватив нь тэгтэй тэнцүү байх цэг бүр нь функцэд экстремум өгдөг гэж бодож болохгүй: зүгээр л заасан шаардлагатай нөхцөл хангалтгүй.

Функцийн хэт туйлшрал

Тодорхойлолт 2

$x_0$ цэгийг $f(x)$ функцийн максимум цэг гэж нэрлэдэг бөгөөд энэ цэгийн хөрш байгаа бөгөөд энэ хөршөөс бүх $x$-д $f(x)\le f(x_0) тэгш бус байдал бий болно. )$ сэтгэл хангалуун байна.

Тодорхойлолт 3

$x_0$ цэгийг $f(x)$ функцийн хамгийн их цэг гэж нэрлэдэг бөгөөд энэ цэгийн хөрш байгаа бөгөөд энэ хөршөөс бүх $x$-д $f(x)\ge f(x_0) тэгш бус байдал бий болно. доллар сэтгэл хангалуун байна.

Функцийн экстремумын тухай ойлголт нь функцийн эгзэгтэй цэгийн тухай ойлголттой нягт холбоотой. Түүний тодорхойлолтыг танилцуулъя.

Тодорхойлолт 4

$x_0$ гэж нэрлэдэг чухал цэг$f(x)$ функцууд хэрэв:

1) $x_0$ - тодорхойлолтын домэйны дотоод цэг;

2) $f"\left(x_0\right)=0$ эсвэл байхгүй байна.

Экстремумын тухай ойлголтын хувьд түүний оршин тогтнох хангалттай, шаардлагатай нөхцлийн талаар теоремуудыг томъёолж болно.

Теорем 2

Хангалттай нөхцөлэкстремум

$x_0$ цэг нь $y=f(x)$ функцийн хувьд чухал байх ба $(a,b)$ интервалд хэвтэнэ. $\left(a,x_0\right)\ ба \ (x_0,b)$ интервал бүр дээр $f"(x)$ дериватив байгаа бөгөөд тогтмол тэмдэг үлдээгээрэй. Дараа нь:

1) Хэрэв $(a,x_0)$ интервал дээр $f"\left(x\right)>0$ дериватив, $(x_0,b)$ интервал дээр $f"\left(x\) дериватив байвал. баруун)

2) Хэрэв $f"\left(x\right)0$ дериватив $(a,x_0)$ интервал дээр байвал $x_0$ цэг нь энэ функцийн хамгийн бага цэг болно.

3) Хэрэв $(a,x_0)$ болон $(x_0,b)$ интервал дээр $f"\left(x\right) >0$ дериватив эсвэл $f"\left(x) үүсмэл байвал \баруун)

Энэ теоремыг 1-р зурагт үзүүлэв.

Зураг 1. Экстремум оршин тогтнох хангалттай нөхцөл

Хэт туйлшралын жишээ (Зураг 2).

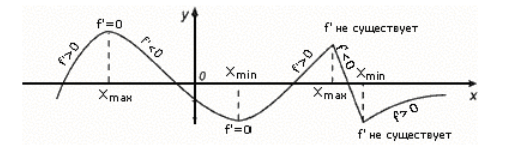
Зураг 2. Экстремум цэгүүдийн жишээ

Функцийг экстремумын хувьд шалгах дүрэм

2) $f"(x)$ деривативыг ол;

7) Теорем 2-ыг ашиглан интервал бүр дээр максимум ба минимум байгаа эсэх талаар дүгнэлт гарга.

Өсөх ба буурах функц

Эхлээд нэмэгдэх ба буурах функцүүдийн тодорхойлолтыг танилцуулъя.

Тодорхойлолт 5

$X$ интервал дээр тодорхойлсон $y=f(x)$ функцийг $x_1-д $x_1,x_2\ X$-ийн аль нэг цэгийн хувьд өсөлт гэж нэрлэдэг.

Тодорхойлолт 6

$X$ интервал дээр тодорхойлсон $y=f(x)$ функцийг $x_1f(x_2)$-д $x_1,x_2\ X$-ийн аль нэг цэгийн хувьд буурах гэж нэрлэдэг.

Өсөх, бууруулах функцийг шалгах

Та дериватив ашиглан нэмэгдүүлэх, багасгах функцуудыг судалж болно.

Функцийн өсөлт ба бууралтын интервалыг шалгахын тулд та дараахь зүйлийг хийх ёстой.

1) $f(x)$ функцийн домайныг ол;

2) $f"(x)$ деривативыг ол;

3) $f"\left(x\right)=0$ тэнцүү байх цэгүүдийг ол;

4) $f"(x)$ байхгүй цэгүүдийг олох;

5) Координатын шугам дээр бүх олдсон цэгүүд болон өгөгдсөн функцийн мужийг тэмдэглэнэ;

6) Үүссэн интервал бүр дээр $f"(x)$ деривативын тэмдгийг тодорхойлох;

7) Дүгнэлт хийнэ үү: $f"\left(x\right)0$ интервалууд дээр функц нэмэгдэх болно.

Өсөлт, бууралт, экстремум цэгүүд байгаа эсэхийг судлах асуудлын жишээ

Жишээ 1

Өсөх ба буурах функц, максимум ба минимум цэг байгаа эсэхийг судал: $f(x)=(2x)^3-15x^2+36x+1$

Эхний 6 оноо ижил тул эхлээд тэдгээрийг зурах болно.

1) Тодорхойлолтын домэйн - бүх бодит тоо;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ нь тодорхойлолтын домэйны бүх цэгүүдэд байдаг;

5) Координатын шугам:

Зураг 3

6) Интервал бүр дээр $f"(x)$ деривативын тэмдгийг тодорхойл.

\ \.

yavl функцийн хүрээ. интервал [ 1; 3].

1. x = -3, x = - 1, x = 1.5, x = 4.5 үед функцийн утга тэг болно.

Функцийн утга тэг байх аргументийн утгыг функцийн тэг гэж нэрлэдэг.

//тэд. Энэ функцийн хувьд -3;-1;1.5; 4.5 нь тэг.

2. Интервалууд дээр [ 4.5; 3) ба (1; 1.5) ба (4.5; 5.5] f функцийн график нь абсцисса тэнхлэгийн дээр байрлах ба абсцисса тэнхлэгийн доор (-3; -1) ба (1.5; 4.5) интервалд энэ нь байна. дараах байдлаар тайлбарлав - [ 4.5; 3) ба (1; 1.5) ба (4.5; 5.5] интервалууд дээр функцийг авна. эерэг утгууд, мөн (-3; -1) ба (1.5; 4.5) интервалууд дээр сөрөг байна.

Заасан интервал бүрийг (функц нь ижил тэмдгийн утгыг авдаг) функцийн тогтмол тэмдгийн интервал гэж нэрлэдэг f.//i.e. жишээ нь (0; 3) интервалыг авбал энэ нь өгөгдсөн функцийн тогтмол тэмдгийн интервал биш юм.

Математикийн хувьд функцийн тэмдгийн тогтмол байдлын интервалыг хайхдаа интервалыг заадаг заншилтай байдаг. хамгийн их урт. //Тэд. интервал (2; 3) байна тогтмол интервалфункц f, гэхдээ хариулт нь интервалыг оруулах ёстой [ 4,5; 3) интервалыг агуулсан (2; 3).

3. Хэрэв та x тэнхлэгийн дагуу 4.5-аас 2 хүртэл шилжих юм бол функцийн график буурч, өөрөөр хэлбэл функцийн утга буурч байгааг анзаарах болно. //Математикт [ 4,5 ; 2] функц буурч байна.

x 2-оос 0 хүртэл өсөхөд функцийн график дээшилнэ, өөрөөр хэлбэл. функцын утгууд нэмэгддэг. //Математикт интервал дээр [ 2; 0] функц нэмэгдэж байна.

Энэ интервалаас x1 ба x2 аргументын хоёр утгын хувьд x2 > x1, f (x2) > f (x1) тэгш бус байдал хангагдах тохиолдолд f функцийг дуудна. // эсвэл Функцийг дуудна тодорхой интервалаар нэмэгддэг, хэрэв энэ интервал дахь аргументийн аль нэг утгуудын хувьд аргументын том утга нь функцийн том утгатай тохирч байвал.//өөрөөр хэлбэл. x их байх тусмаа у.

f функцийг дуудна тодорхой интервалаар буурч байна, хэрэв энэ интервалаас x1 ба x2 аргументын аль нэг хоёр утгын хувьд x2 > x1 байх тохиолдолд зарим интервал дээр буурах f(x2) тэгш бус байдал хангагдана, хэрэв энэ интервалаас аргументийн аль нэг утгын хувьд илүү их байвал аргументын утга нь функцийн бага утгатай тохирч байна. //тэд. x их байх тусмаа у бага.

Хэрэв функц бүхэл бүтэн тодорхойлолтын хүрээнд нэмэгдэж байвал түүнийг дуудна нэмэгдэх.

Хэрэв функц бүхэл бүтэн тодорхойлолтын хүрээнд буурч байвал түүнийг дуудна суларч байна.

Жишээ 1нэмэгдэх ба буурах функцүүдийн график.

Жишээ 2

Yavl-ийг тодорхойлно уу. f(x) = 3x + 5 шугаман функц нэмэгдэж байна уу эсвэл буурч байна уу?

Баталгаа. Тодорхойлолтуудыг ашиглацгаая. x1 ба x2 нь аргументийн дурын утгууд ба x1 байг< x2., например х1=1, х2=7