රේඛීය මැදිහත්වීමේ ක්‍රමය භාවිතයෙන් අතරමැදි අගය නිර්ණය කිරීම. Microsoft Excel හි Extrapolation භාවිතා කිරීම

මෙම පදයට වෙනත් අර්ථයන් ඇත, අන්තර් සම්බන්ධනය බලන්න. ශ්‍රිතය ගැන, බලන්න: Interpolant.

ඉන්ටර්පෝලේෂන්, මැදිහත් වීම (සිට lat. අන්තර් පොලිස් - « සිනිඳු, අලුත් කරන ලද, අලුත් කරන ලද; පරිවර්තනය කළා") - පරිගණක ගණිතයේ, දැනට පවතින විවික්ත අගයන් සමූහයකින් ප්‍රමාණයක අතරමැදි අගයන් සෙවීමේ ක්‍රමයකි. "ඉන්ටර්පෝලේෂන්" යන යෙදුම මුලින්ම භාවිතා කරන ලද්දේ ජෝන් වොලිස් විසින් ඔහුගේ "අනන්තයේ අංක ගණිතය" (1656) යන නිබන්ධනයේ ය.

ක්‍රියාකාරී විශ්ලේෂණයේදී, අන්තර් ක්‍රියාකාරිත්වය රේඛීය ක්රියාකරුවන්යනු Banach අවකාශයන් යම් කාණ්ඩයක අංග ලෙස සලකන කොටසකි.

විද්‍යාත්මක සහ ඉංජිනේරු ගණනය කිරීම් සමඟ කටයුතු කරන බොහෝ දෙනෙකුට බොහෝ විට ක්‍රියා කිරීමට සිදු වන්නේ ආනුභවිකව හෝ අහඹු නියැදීමකින් ලබාගත් අගයන් සමූහයක් සමඟිනි. රීතියක් ලෙස, මෙම කට්ටල මත පදනම්ව, එය විය හැකි ශ්රිතයක් ගොඩනැගීමට අවශ්ය වේ ඉහළ නිරවද්යතාවඅනෙකුත් ප්රතිඵල අගයන් පහර. මෙම ගැටළුව ආසන්න වශයෙන් හැඳින්වේ. ඉන්ටර්පෝලේෂන් යනු තනන ලද ශ්‍රිතයේ වක්‍රය හරියටම පවතින දත්ත ලක්ෂ්‍ය හරහා ගමන් කරන ආසන්න ආකාරයකි.

ඉන්ටර්පෝලේෂන් වලට ආසන්න කාර්යයක් ද ඇත, එය සමහරක් ආසන්න වශයෙන් සමන්විත වේ සංකීර්ණ කාර්යයතවත්, සරල කාර්යයක්. යම් කාර්යයක් ඵලදායී ගණනය කිරීම් සඳහා ඉතා සංකීර්ණ නම්, ඔබට එහි අගය ලක්ෂ්‍ය කිහිපයකින් ගණනය කිරීමට උත්සාහ කළ හැකි අතර, ඒවායින් ඉන්ටර්පෝලේට්, සරල ශ්‍රිතයක් ගොඩනඟන්න. ඇත්ත වශයෙන්ම, සරල කළ කාර්යයක් භාවිතා කිරීමෙන් ඔබට එයම ලබා ගැනීමට ඉඩ නොදේ නිවැරදි ප්රතිඵල, මුල් කාර්යය ලබා දෙනු ඇත. නමුත් සමහර පන්තිවල ගැටළු වලදී, ගණනය කිරීම් වල සරල බව සහ වේගයේ අත්කර ගත් ප්‍රතිඵලය ප්‍රතිඵලයේ ඇති වන දෝෂයට වඩා වැඩි විය හැක.

එසේම සඳහන් කළ යුතු කරුණක් වන්නේ operator interpolation ලෙස හැඳින්වෙන හාත්පසින්ම වෙනස් ආකාරයේ ගණිතමය මැදිහත්වීමක් වේ. ක්‍රියාකරු අන්තර් ක්‍රියාකාරිත්වය පිළිබඳ සම්භාව්‍ය කෘතීන් අතර Riesz-Thorin ප්‍රමේයය සහ අනෙකුත් බොහෝ කෘති සඳහා පදනම වන Marcinkiewicz ප්‍රමේයය ඇතුළත් වේ.

අර්ථ දැක්වීම්

සමහර කලාපයෙන් D (\displaystyle x_(i)) (i ∈ 0 , 1 , … , N (\ displaystyle i\in (0,1,\dots ,N))) සමපාත නොවන ලකුණු පද්ධතියක් සලකා බලන්න ( \displaystyle D) . f (\ displaystyle f) ශ්‍රිතයේ අගයන් මෙම ලක්ෂ්‍යවලදී පමණක් දැන ගැනීමට ඉඩ දෙන්න:

Y i = f (x i) , i = 1 , … , N . (\ displaystyle y_(i)=f(x_(i)),\quad i=1,\ldots ,N.)

අන්තර් ඛණ්ඩනය කිරීමේ ගැටලුව නම්, ලබා දී ඇති ශ්‍රිත පන්තියකින් F (\ displaystyle F) ශ්‍රිතයක් සොයා ගැනීමයි.

F (x i) = y i, i = 1, ..., N. (\displaystyle F(x_(i))=y_(i),\quad i=1,\ldots ,N.)

• ලකුණු x i (\displaystyle x_(i)) ලෙස හැඳින්වේ ඉන්ටර්පෝලේෂන් නෝඩ්, සහ ඔවුන්ගේ සම්පූර්ණත්වය වේ interpolation ජාලකය.
• යුගල (x i , y i) (\displaystyle (x_(i),y_(i))) ලෙස හැඳින්වේ දත්ත ලකුණුහෝ මූලික කරුණු.
• "අසල්වැසි" අගයන් අතර වෙනස Δ x i = x i - x i - 1 (\ displaystyle \Delta x_(i)=x_(i)-x_(i-1)) - interpolation ජාල පියවර. එය විචල්‍ය හෝ නියත විය හැක.
• ශ්‍රිතය F (x) (\displaystyle F(x)) - අන්තර් හුවමාරු ශ්‍රිතයහෝ අන්තර් පොලන්තය.

උදාහරණයක්

1. අපට ඉඩ දෙන්න වගු කාර්යය, පහත විස්තර කර ඇති ආකාරයට, x (\ displaystyle x) අගයන් කිහිපයක් සඳහා f (\ displaystyle f) හි අනුරූප අගයන් තීරණය කරයි:

X (\ displaystyle x) f (x) (\ displaystyle f(x))

0
1	0,8415
2	0,9093
3	0,1411
4	−0,7568
5	−0,9589
6	−0,2794

එවැනි ශ්‍රිතයකට නිශ්චිත ලක්ෂ්‍ය හැර වෙනත් ලක්ෂ්‍යයක තිබිය හැකි අගය කුමක්දැයි දැන ගැනීමට අන්තර් පොලනය අපට උපකාර කරයි (උදාහරණයක් ලෙස, විට x = 2,5).

මේ වන විට බොහෝ ඇත විවිධ ආකාරවලින්මැදිහත් වීම. වඩාත්ම සුදුසු ඇල්ගොරිතම තේරීම ප්‍රශ්නවලට පිළිතුරු මත රඳා පවතී: තෝරාගත් ක්‍රමය කෙතරම් නිවැරදිද, එය භාවිතා කිරීමේ පිරිවැය කොපමණද, අන්තර් ක්‍රියාකාරිත්වය කෙතරම් සුමටද, එයට අවශ්‍ය දත්ත ලකුණු කීයක් යනාදිය.

2. අතරමැදි අගය සොයා ගන්න (රේඛීය මැදිහත්වීම මගින්).

6000	15.5
6378	?
8000	19.2

15.5 + (6378 - 6000) 8000 - 6000 ∗ (19.2 - 15.5) 1 = 16.1993 (\ displaystyle ?=15.5+(\frac ((6378-6000)-(6378-6000)) (2000) 15.5))(1))=16.1993)

ක්‍රමලේඛන භාෂා වලින්

y = 3 x + x 2 (\displaystyle y=3x+x^(2)) ශ්‍රිතය සඳහා රේඛීය අන්තර් ක්‍රියාකාරිත්වයේ උදාහරණයක්. පරිශීලකයාට 1 සිට 10 දක්වා අංකයක් ඇතුළත් කළ හැකිය.

ෆෝට්‍රාන්

වැඩසටහන interpol integer i real x, y, xv, yv, yv2 මානය x(10) මානය y(10) call prisv(x, i) call func(x, y, i) write(*,*) "අංකය ඇතුලත් කරන්න: " කියවන්න(*,*) xv නම් ((xv >= 1).සහ.(xv xv)) පසුව yv2 = ((xv - x(i)) * (y(i+1) - y(i)) / (x(i+1) - x(i))) + y(i) end if end do end subroutine

C++

int main() ( system("COLOR 0A"); double ob, x1, x2, y1, y2, p1, p2, pi, skolko, status; system("echo Interpolation X1 - X2 "); system("echo Enter අංකය: "); cin >> ob; system("echo උදාහරණයක් ලෙස 62, C1 = 60, L1 = 1.31, C2 = 80, L2 = 1.29"); cout > x1; cout > x2; cout > y1; cout > y2 ; p1 = y1 - x1; p2 = y2 - x2; pi = p2 / p1; skolko = ob - x1; තත්ත්වය = x2 + (pi * skolko); cout

ඉන්ටර්පෝලේෂන් ක්රම

ආසන්නතම අසල්වැසි මැදිහත්වීම

සරළම අන්තර් ඡේදනය කිරීමේ ක්‍රමය වන්නේ ආසන්නතම අසල්වැසි අන්තර් ක්‍රමයයි.

බහුපද මගින් අන්තර් බන්ධනය

ප්රායෝගිකව, බහුපද මගින් අන්තර් බන්ධනය බොහෝ විට භාවිතා වේ. මෙයට මූලික වශයෙන් හේතු වී ඇත්තේ බහුපද ගණනය කිරීමට පහසු වීම, ඒවායේ ව්‍යුත්පන්නයන් විශ්ලේෂණාත්මකව සොයා ගැනීමට පහසු වීම සහ බහුපද මාලාව අභ්‍යවකාශයේ ඝන වීම අඛණ්ඩ කාර්යයන්(වීර්ස්ට්‍රාස් ප්‍රමේයය).

• රේඛීය මැදිහත්වීම
• නිව්ටන්ගේ අන්තර් ඡේදනය සූත්‍රය
• පරිමිත වෙනස ක්රමය
• IMN-1 සහ IMN-2
• Lagrange බහුපද (interpolation polynomial)
• Aitken යෝජනා ක්රමය
• Spline කාර්යය
• ඝන ස්ප්ලයින්

ප්‍රතිලෝම මැදිහත්වීම (x ලබා දී ඇති y ගණනය කිරීම)

• Lagrange බහුපද
• නිව්ටන්ගේ සූත්‍රය භාවිතා කරමින් ප්‍රතිලෝම අන්තර් ක්‍රියාකාරිත්වය
• Gauss සූත්‍රය භාවිතා කරමින් ප්‍රතිලෝම මැදිහත්වීම

විචල්‍ය කිහිපයක ශ්‍රිතයක අන්තර් ක්‍රියාකාරිත්වය

• Bilinear interpolation
• Bicubic interpolation

වෙනත් මැදිහත්වීම් ක්රම

• තාර්කික මැදිහත්වීම
• ත්‍රිකෝණමිතික මැදිහත්වීම

අදාළ සංකල්ප

• Extrapolation - දී ඇති පරතරයකින් පිටත ලක්ෂ්‍ය සොයා ගැනීමේ ක්‍රම (වක්‍රය දිගුව)
• ආසන්න කිරීම - ආසන්න වක්ර ඉදිකිරීම සඳහා ක්රම

ප්‍රතිලෝම මැදිහත්වීම

අරාවේ (xi, yi) ලක්ෂ්‍ය හරහා ගමන් කරන ප්‍රස්ථාර C2 අවකාශයෙන් ශ්‍රිත පන්තිය මත, i = 0, 1, . . . , එම්.

විසඳුමක්. යොමු ලක්ෂ්‍ය (xi, f(xi)) හරහා ගමන් කරන සහ සඳහන් කළ අවකාශයට අයත් සියලුම ශ්‍රිතයන් අතර, එය S00(a) = S00(b) = 0 යන මායිම් කොන්දේසි තෘප්තිමත් කරමින් cubic spline S(x) වේ. , එය අන්ත (අවම) ක්‍රියාකාරී I(f) සපයයි.

බොහෝ විට ප්‍රායෝගිකව ගැටලුව පැන නගින්නේ ශ්‍රිතයක දී ඇති අගයක් භාවිතා කරමින් තර්කයක අගය සෙවීමයි. මෙම ගැටළුව විසඳනු ලබන්නේ ප්රතිලෝම මැදිහත්වීම් ක්රම මගිනි. නම් ලබා දී ඇති කාර්යයඒකාකාරී වේ, එවිට ප්‍රතිලෝම මැදිහත්වීම ඉතා පහසුවෙන් සිදු කරනු ලබන්නේ ශ්‍රිතය තර්කයකින් සහ අනෙක් අතට ප්‍රතිස්ථාපනය කිරීමෙන් පසුව අන්තර් ඛණ්ඩනය කිරීමෙනි. ලබා දී ඇති කාර්යය ඒකාකාරී නොවේ නම්, මෙම තාක්ෂණය භාවිතා කළ නොහැක. ඉන්පසුව, ශ්රිතයේ සහ තර්කයේ භූමිකාවන් වෙනස් නොකර, අපි එක් හෝ තවත් අතුරු සූත්රයක් ලියන්නෙමු; භාවිතා කරමින් දන්නා අගයන්තර්කය සහ, ශ්‍රිතය දන්නා බව උපකල්පනය කරමින්, තර්කයට අදාළව ලැබෙන සමීකරණය අපි විසඳමු.

පළමු තාක්‍ෂණය භාවිතා කරන විට ඉතිරි පදය ඇගයීම සෘජු අන්තර් ක්‍රියාකාරිත්වයට සමාන වේ, සෘජු ශ්‍රිතයේ ව්‍යුත්පන්නයන් පමණක් ප්‍රතිලෝම ශ්‍රිතයේ ව්‍යුත්පන්නයන් මගින් ප්‍රතිස්ථාපනය කළ යුතුය. දෙවන ක්රමයේ දෝෂය තක්සේරු කරමු. අපට f(x) ශ්‍රිතයක් ලබා දෙන්නේ නම් සහ Ln (x) යනු x0, x1, x2, නෝඩ් වලින් මෙම ශ්‍රිතය සඳහා ගොඩනගා ඇති Lagrange interpolation polynomial වේ. . . , xn, පසුව

f (x) - Ln (x) =(n + 1)! (x− x0) . . . (x− xn) .

අපි හිතමු අපි f (¯x) = y¯ (y¯ ලබා දී ඇති) x¯ හි අගය සොයා ගත යුතුයි. අපි Ln (x) = y¯ සමීකරණය විසඳන්නෙමු. අපි x¯ අගයක් ගනිමු. පෙර සමීකරණයට ආදේශ කිරීමෙන්, අපට ලැබෙන්නේ:

Mn+1

f (x¯) - Ln (x¯) = f (x¯) - y¯ = f (x¯) - f (¯x) =
Langrange හි සූත්‍රය යෙදීමෙන් අපට ලැබේ
(x¯ - x¯) f0 (η) =
මෙහි η x¯ සහ x¯ අතර වේ. x¯ සහ x¯ සහ min අඩංගු විරාමයක් නම්

අවසාන ප්රකාශනයේ සිට එය පහත දැක්වේ:

|x¯ - x¯| 6m1(n+1)! |$n(x¯)| .

මෙම අවස්ථාවේදී, ඇත්ත වශයෙන්ම, අපි Ln (x) = y¯ සමීකරණය නිවැරදිව විසඳා ඇති බව උපකල්පනය කෙරේ.

වගු නිර්මාණය කිරීම සඳහා මැදිහත්වීම භාවිතා කිරීම

ශ්‍රිත වගු සම්පාදනය කිරීමේදී අන්තර්පෝලන න්‍යායට යෙදුම් ඇත. එවැනි ගැටලුවක් ලැබුණු පසු, ගණිතඥයා ගණනය කිරීම් ආරම්භ කිරීමට පෙර ප්රශ්න ගණනාවක් විසඳිය යුතුය. ගණනය කිරීම් සිදු කරනු ලබන සූත්‍රයක් තෝරා ගත යුතුය. මෙම සූත්‍රය අඩවියෙන් අඩවියට වෙනස් විය හැක. සාමාන්‍යයෙන්, ශ්‍රිත අගයන් ගණනය කිරීම සඳහා වන සූත්‍ර අපහසු වන අතර එම නිසා ඒවා සමහර යොමු අගයන් ලබා ගැනීමට භාවිතා කරන අතර පසුව උප වගුගත කිරීම මගින් වගුව ඝනීභවනය වේ. ශ්‍රිතයේ යොමු අගයන් ලබා දෙන සූත්‍රය පහත උප වගු සැලකිල්ලට ගනිමින් වගු වල අවශ්‍ය නිරවද්‍යතාවය සැපයිය යුතුය. ඔබට නියත පියවරක් සමඟ වගු සෑදීමට අවශ්‍ය නම්, ඔබ මුලින්ම එහි පියවර තීරණය කළ යුතුය.

Back First Previous ඊළඟට අන්තිමට Index වෙත යන්න

බොහෝ විට, ශ්‍රිත වගු සම්පාදනය කරනු ලබන්නේ රේඛීය අන්තර් බන්ධනය (එනම්, ටේලර් සූත්‍රයේ පළමු පද දෙක භාවිතා කර අන්තර් සම්බන්ධ කිරීම) හැකි වන පරිදි ය. මෙම අවස්ථාවේදී, ඉතිරි පදයට පෝරමය ඇත

R1 (x) =f00 (ξ)h2t(t - 1).

මෙහි ξ අයත් වන්නේ තර්කයේ යාබද වගු අගයන් දෙකක් අතර පරතරයට වන අතර, එහි x පිහිටා ඇති අතර t යනු 0 සහ 1 අතර වේ. නිෂ්පාදනය t (t - 1) විශාලතම මොඩියුලය ගනී.

අගය t = 12. මෙම අගය 14 වේ. ඒ නිසා,

මෙම දෝෂය සමඟ - ක්‍රමයේ දෝෂය - අතරමැදි අගයන් ප්‍රායෝගිකව ගණනය කිරීමේදී, ඉවත් කළ නොහැකි දෝෂයක් සහ වටකුරු දෝෂයක් ද පැන නගින බව මතක තබා ගත යුතුය. අප කලින් දැක ඇති පරිදි, රේඛීය අන්තර් ක්‍රියාකාරිත්වයේ මාරක දෝෂය වගුගත ශ්‍රිත අගයන්හි දෝෂයට සමාන වේ. වටකුරු දෝෂය මත රඳා පවතී පරිගණක පහසුකම්සහ ගණනය කිරීමේ වැඩසටහනෙන්.

Back First Previous ඊළඟට අන්තිමට Index වෙත යන්න

විෂය දර්ශකය

දෙවන අනුපිළිවෙලෙහි වෙන් වූ වෙනස්කම්, 8 පළමු අනුපිළිවෙල, 8

ස්ප්ලයින්, 15

ඉන්ටර්පෝලේෂන් නෝඩ්, 4

Back First Previous ඊළඟට අන්තිමට Index වෙත යන්න

/ Material_studentam_po_RGR_BZhD / මැදිහත්වීම සිදු කරන්නේ කෙසේද

වගු දත්ත අන්තර් හුවමාරු කිරීම සඳහා සූත්‍රය

කොන්දේසියෙන් NHR (Q, t) ප්‍රමාණය වූ විට, 2 වන ක්‍රියාවෙහි භාවිතා වේ අතර අතරමැදි වේටී 100 සහ ටී 300.

(ව්යතිරේක:කොන්දේසිය අනුව Q 100 හෝ 300 ට සමාන නම්, ඉන්ටර්පෝලේෂන් අවශ්ය නොවේ).

y o- තත්ත්වයෙන් ඔබේ මූලික NHR ප්‍රමාණය, ටොන් වලින්

(Q අකුරට අනුරූප වේ)

y 1 – කුඩා

(වගුව 11-16 සිට, සාමාන්යයෙන් 100 ට සමාන වේ).

y 2 – තව ඔබට ආසන්නතම NHR ප්‍රමාණයේ වටිනාකම ටොන් වලින්

(වගුව 11-16 සිට, සාමාන්යයෙන් 300 ට සමාන වේ).

x 1 y 1 (x 1 ප්රතිවිරුද්ධව පිහිටා ඇත y 1 ), කි.මී.

x 2 - පිළිවෙලින් දූෂිත වායු වලාකුළක (Gt) බෙදා හැරීමේ ගැඹුරේ වගු අගය y 2 (x 2 ප්රතිවිරුද්ධව පිහිටා ඇත y 2 ), කි.මී.

x 0 - අවශ්ය අගය ජී ටීසුදුසු y o(සූත්රය අනුව).

උදාහරණයක්.

NHR - ක්ලෝරීන්; Q = 120 ටී;

SVSP වර්ගය (සිරස් වායු ප්රතිරෝධයේ උපාධිය) - ප්රතිලෝම.

සොයන්න ජී ටී- දූෂිත වාතය වලාකුළක් බෙදා හැරීමේ ගැඹුරේ වගු අගය.

අපි 11-16 වගු හරහා බලා ඔබගේ තත්වයට ගැලපෙන දත්ත සොයා ගනිමු (ක්ලෝරීන්, ප්‍රතිලෝම).

වගුව 11 සුදුසු වේ.

අගයන් තෝරා ගැනීම y 1 , y 2, x 1 , x 2 . වැදගත් - සුළගේ වේගය 1 m/s ලෙස ගන්න, උෂ්ණත්වය 20 °C ලෙස ගන්න.

අපි තෝරාගත් අගයන් සූත්‍රයට ආදේශ කර සොයා ගනිමු x 0 .

වැදගත් - ගණනය කිරීම නිවැරදි නම් x 0 අතර කොහේ හරි අගයක් ඇත x 1 , x 2 .

1.4 Lagrange interpolation සූත්රය

ලැග්‍රේන්ජ් විසින් අන්තර් පොලේටින් තැනීම සඳහා යෝජනා කරන ලද ඇල්ගොරිතමය

වගු (1) වෙතින් වන ශ්‍රිත මඟින් පෝරමයෙහි අන්තර් විස්ථාපනය බහුපද Ln(x) තැනීම සඳහා සපයයි.

පැහැදිලිවම, (10) සඳහා කොන්දේසි (11) ඉටු කිරීම, අන්තර් සම්බන්ධක ගැටලුව සැකසීම සඳහා කොන්දේසි (2) ඉටු කිරීම තීරණය කරයි.

බහුපද li(x) පහත පරිදි ලියා ඇත

සූත්‍රයේ (14) හරයේ එක සාධකයක්වත් බිංදුවට සමාන නොවන බව සලකන්න. නියත ci හි අගයන් ගණනය කිරීමෙන් පසු, ඔබට ලබා දී ඇති ලක්ෂ්‍යවල අන්තර් පොලිත ශ්‍රිතයේ අගයන් ගණනය කිරීමට ඒවා භාවිතා කළ හැකිය.

සූත්‍ර (13) සහ (14) සැලකිල්ලට ගනිමින් Lagrange අන්තර් ධ්‍රැව බහුපද (11) සඳහා සූත්‍රය මෙසේ ලිවිය හැකිය.

qi (x - x0)(x - x1) K (x - xi -1)(x - xi +1) K (x - xn)

1.4.1.Lagrange සූත්රය භාවිතයෙන් අතින් ගණනය කිරීම් සංවිධානය කිරීම

Lagrange සූත්‍රයේ සෘජු යෙදුම සමාන ගණනය කිරීම් විශාල සංඛ්‍යාවක් කරා යොමු කරයි. කුඩා ප්රමාණයේ වගු සඳහා, මෙම ගණනය කිරීම් අතින් හෝ වැඩසටහන් පරිසරයක් තුළ සිදු කළ හැකිය

පළමු අදියරේදී, අපි අතින් ගණනය කිරීම් සඳහා ඇල්ගොරිතමයක් සලකා බලමු. අනාගතයේදී, මෙම ගණනය කිරීම් පරිසරය තුළ නැවත නැවතත් කළ යුතුය

Microsoft Excel හෝ OpenOffice.org Calc.

රූපයේ. රූප සටහන 6 හි දැක්වෙන්නේ නෝඩ් හතරකින් නිර්වචනය කරන ලද අන්තර් සම්බන්ධිත ශ්‍රිතයක මුල් වගුවේ උදාහරණයකි.

Fig.6. අන්තර් සම්බන්ධිත ශ්‍රිතයේ නෝඩ් හතරක් සඳහා මූලික දත්ත අඩංගු වගුව

වගුවේ තුන්වන තීරුවේ අපි සූත්‍ර (14) භාවිතයෙන් ගණනය කරන ලද qi සංගුණකවල අගයන් ලියන්නෙමු. පහත දැක්වෙන්නේ n=3 සඳහා මෙම සූත්‍රවල වාර්තාවකි.

q0=Y0/(x0-x1)/(x0-x2)/(x0-x3)q1=Y1/(x1-x0)/(x1-x2)/(x1-x3)(16) q2=Y2/( x2-x0)/(x2-x1)/(x2-x3)q3=Y3/(x3-x0)/(x3-x1)/(x3-x2)

අතින් ගණනය කිරීම් ක්‍රියාත්මක කිරීමේ ඊළඟ පියවර වන්නේ සූත්‍ර (13) අනුව සිදු කරන ලද li(x) (j=0,1,2,3) අගයන් ගණනය කිරීමයි.

අපි සලකා බලන නෝඩ් හතරක් සහිත වගුවේ අනුවාදය සඳහා මෙම සූත්‍ර ලියන්නෙමු:

l0(x)=q0(x-x1)·(x-x2)·(x-x3),

l1(x)=q1(x-x0)·(x-x2)·(x-x3),

l2(x)=q2(x-x0)·(x-x1)·(x-x3),(17) l3(x)=q3(x-x0)·(x-x1)·(x-x2) .

අපි li(xj) (j=0,1,2,3) බහුපද වල අගයන් ගණනය කර වගු කොටු වල ලියන්නෙමු. සූත්‍රය (11) අනුව Ycalc(x) ශ්‍රිතයේ අගයන් පේළියෙන් li(xj) අගයන් සාරාංශ කිරීමේ ප්‍රතිඵලයක් ලෙස ලැබේ.

ගණනය කළ අගයන් li(xj) සහ Ycalc(x) අගයන්හි තීරු ඇතුළුව වගුවේ ආකෘතිය රූපය 8 හි පෙන්වා ඇත.

සහල්. 8. තර්කයේ xi හි සියලුම අගයන් සඳහා සූත්‍ර (16), (17) සහ (11) භාවිතයෙන් සිදු කරන ලද අතින් ගණනය කිරීම් වල ප්‍රතිඵල සහිත වගුව

රූපයේ දැක්වෙන වගුව ජනනය කිරීමෙන් පසුව. 8, සූත්‍ර (17) සහ (11) භාවිතා කරමින් ඔබට X තර්කයේ ඕනෑම අගයක් සඳහා අන්තර් සම්බන්ධිත ශ්‍රිතයේ අගය ගණනය කළ හැක. උදාහරණයක් ලෙස, X=1 සඳහා අපි li(1) (i=0,) අගයන් ගණනය කරමු. 1,2,3):

l0(1)= 0.7763; l1(1)= 3.5889; l2(1)=-1.5155;l3(1)= 0.2966.

li(1) හි අගයන් සාරාංශ කිරීමෙන් අපි Yinterp(1)=3.1463 අගය ලබා ගනිමු.

1.4.2 මයික්‍රොසොෆ්ට් එක්සෙල් වැඩසටහන් පරිසරය තුළ Lagrange සූත්‍ර භාවිතා කරමින් අන්තර් ක්‍රියා කිරීමේ ඇල්ගොරිතමයක් ක්‍රියාත්මක කිරීම

අත්පොත ගණනය කිරීම් වලදී මෙන්, ඉන්ටර්පෝලේෂන් ඇල්ගොරිතම ක්‍රියාත්මක කිරීම ආරම්භ වන්නේ රූපයේ qi සංගුණක ගණනය කිරීම සඳහා සූත්‍ර ලිවීමෙනි. රූප සටහන 9 මඟින් තර්කයේ ලබා දී ඇති අගයන්, අන්තර් පොලිත ශ්‍රිතය සහ සංගුණක qi සමඟ වගු තීරු පෙන්වයි. මෙම වගුවේ දකුණු පසින් qi සංගුණකවල අගයන් ගණනය කිරීම සඳහා C තීරුවේ සෛලවල ලියා ඇති සූත්‍ර ඇත.

ВС2: "=B2/((A2-A3)*(A2-A4)*(A2-A5))" Ж q0

ВС3: "=B3/((A3-A4)*(A3-A5)*(A3-A2))" Ж q1

ВС4: "=B4/((A4-A5)*(A4-A2)*(A4-A3))" Ж q2

ВС5: "=B5/((A5-A2)*(A5-A3)*(A5-A4))" Ж q3

සහල්. 9 සංගුණක qi සහ ගණනය කිරීමේ සූත්‍ර වගුව

C2 සෛලයේ q0 සූත්‍රය ඇතුළත් කිරීමෙන් පසු එය C3 සිට C5 දක්වා සෛල හරහා දිගු වේ. ඉන්පසු මෙම සෛලවල ඇති සූත්‍ර (16) රූපයේ දැක්වෙන පෝරමයට අනුව සකස් කරනු ලැබේ. 9.

Ycalc(xi),

සූත්‍ර (17) ක්‍රියාත්මක කරමින්, D, E, F සහ G තීරු වල සෛලවල li (x) (i=0,1,2,3) අගයන් ගණනය කිරීම සඳහා අපි සූත්‍ර ලියන්නෙමු. අගය ගණනය කිරීම සඳහා D2 කොටුවේ l0(x0) අපි සූත්‍රය ලියන්නෙමු:

=$C$2*($A2-$A$3)*($A2-$A$4)*($A2-$A$5),

අපි l0 (xi) (i=0,1,2,3) අගයන් ලබා ගනිමු.

Li(x0) (i=1,2,3) ගණනය කිරීම සඳහා ගණනය කිරීමේ සූත්‍ර සෑදීමට $A2 සබැඳි ආකෘතිය මඟින් E, F, G තීරු හරහා සූත්‍රය දිගු කිරීමට ඔබට ඉඩ සලසයි. ඔබ පේළියක් හරහා සූත්‍රයක් ඇදගෙන ගිය විට, තර්ක තීරුවේ දර්ශකය වෙනස් නොවේ. l0(x0) සූත්‍රය ඇඳීමෙන් පසු li(x0) (i=1,2,3) ගණනය කිරීම සඳහා සූත්‍ර (17) අනුව ඒවා නිවැරදි කිරීම අවශ්‍ය වේ.

H තීරුවේ අපි තබමු එක්සෙල් සූත්‍රසූත්‍රය භාවිතා කරමින් li(x) එකතු කිරීමට

(11)ඇල්ගොරිතම.

රූපයේ. රූපය 10 පරිසරය තුළ ක්රියාත්මක කරන ලද වගුවක් පෙන්වයි Microsoft වැඩසටහන්එක්සෙල්. වගුවේ සෛලවල ලියා ඇති සූත්‍රවල නිරවද්‍යතාවයේ සලකුණක් සහ සිදු කරන ලද ගණනය කිරීමේ ක්‍රියාවන් ප්‍රතිඵලයක් ලෙස ලැබෙන විකර්ණ න්‍යාසය li(xj) (i=0,1,2,3),(j=0,1,2, 3), රූපයේ පෙන්වා ඇති ප්රතිඵල නැවත නැවත කිරීම. 8, සහ ප්‍රභව වගුවේ නෝඩ් වල අන්තර් පොලිත ශ්‍රිතයේ අගයන් සමග සමපාත වන අගයන් තීරුවක්.

සහල්. 10. li(xj) (j=0,1,2,3) සහ Ycalc(xj) අගයන් වගුව

සමහර අතරමැදි ස්ථානවල අගයන් ගණනය කිරීම සඳහා එය ප්රමාණවත් වේ

A තීරුවේ සෛල තුළ, A6 කොටුවෙන් ආරම්භ වන අතර, ඔබට අන්තර් සම්බන්ධිත ශ්‍රිතයේ අගයන් තීරණය කිරීමට අවශ්‍ය X තර්කයේ අගයන් ඇතුළත් කරන්න. තෝරන්න

වගුවේ අවසාන (5 වන) පේළියේ, සෛල l0(xn) සිට Ycalc(xn) දක්වා සහ තෝරාගත් සෛලවල ලියා ඇති සූත්‍ර අවසාන කොටස අඩංගු රේඛාව දක්වා දිගු කරන්න.

x තර්කයේ නිශ්චිත අගය.

රූපයේ. 11 හි ශ්‍රිත අගය ලක්ෂ්‍ය තුනකින් ගණනය කරන වගුවක් පෙන්වයි: x=1, x=2 සහ x=3. මූලාශ්‍ර දත්ත වගුවේ පේළි අංක සමඟ අතිරේක තීරුවක් වගුවට හඳුන්වා දී ඇත.

සහල්. 11. Lagrange සූත්‍ර භාවිතා කරමින් අන්තර් සම්බන්ධිත ශ්‍රිතවල අගයන් ගණනය කිරීම

ප්‍රතිපෝෂණයේ ප්‍රතිඵල ප්‍රදර්ශනය කිරීමේ වැඩි පැහැදිලිකම සඳහා, අපි ආරෝහණ අනුපිළිවෙලට අනුපිළිවෙලට අනුපිළිවෙලින් විස්තාරක X අගයන් තීරුවක්, Y (X) ශ්‍රිතයේ ආරම්භක අගයන් තීරුවක් සහ තීරුවක් ඇතුළත් වගුවක් ගොඩනඟමු.

තාප ගති විද්‍යාවේ (තාප ඉංජිනේරු විද්‍යාවේ) ගැටළු විසඳීමේදී අන්තර් ක්‍රියා සූත්‍රය භාවිතා කරන්නේ කෙසේදැයි මට කියන්න.

අයිවන් ෂෙස්ටාකොවිච්

සරලම, නමුත් බොහෝ විට ප්‍රමාණවත් නොවන ප්‍රමාණවත් අන්තර් නිරෝධනය රේඛීය වේ. ඔබට දැනටමත් දන්නා ලක්ෂ්‍ය දෙකක් (X1 Y1) සහ (X2 Y2) ඇති විට සහ X1 සහ X2 අතර පිහිටා ඇති සමහර X හි දවසේ Y අගයන් සොයා ගැනීමට ඔබට අවශ්‍ය වේ. එවිට සූත්රය සරලයි.
Y=(U2-U1)*(X-X1)/(X2-X1)+Y1
මාර්ගය වන විට, මෙම සූත්‍රය X1..X2 පරතරයෙන් පිටත X අගයන් සඳහාද ක්‍රියා කරයි, නමුත් මෙය දැනටමත් Extrapolation ලෙස හඳුන්වන අතර මෙම පරතරයෙන් සැලකිය යුතු දුරකින් එය ඉතා විශාල දෝෂයක් ලබා දෙයි.
තවත් බොහෝ පරුෂ වචන තිබේ. මැදිහත්වීමේ ක්‍රම - පෙළපොතක් කියවීමට හෝ අන්තර්ජාලය පිරික්සීමට මම ඔබට උපදෙස් දෙමි.
ග්‍රැෆික් මැදිහත්වීමේ ක්‍රමය ද කළ හැකිය - දන්නා ලක්ෂ්‍ය හරහා අතින් ප්‍රස්ථාරයක් අඳින්න සහ අවශ්‍ය X සඳහා ප්‍රස්ථාරයෙන් Y සොයා ගන්න. ;)

නවකතාව

ඔබට අර්ථ දෙකක් ඇත. සහ ආසන්න වශයෙන් යැපීම (රේඛීය, හතරැස්, ..)
මෙම ශ්‍රිතයේ ප්‍රස්ථාරය ඔබගේ ලක්ෂ්‍ය දෙක හරහා ගමන් කරයි. ඔබට අතර කොතැනක හෝ අගයක් අවශ්‍ය වේ. හොඳයි, ඔබ එය ප්රකාශ කරන්න!
උදාහරණ වශයෙන්. වගුවෙහි, අංශක 22 ක උෂ්ණත්වයකදී, සංතෘප්ත වාෂ්ප පීඩනය 120,000 Pa, සහ 26, 124,000 Pa වේ. එවිට අංශක 23 ක උෂ්ණත්වයකදී 121000 Pa.

ඉන්ටර්පෝලේෂන් (ඛණ්ඩාංක)

සිතියමේ (රූපය) සම්බන්ධීකරණ ජාලයක් ඇත.
එහි ප්‍රසිද්ධ යොමු ලක්ෂ්‍ය කිහිපයක් (n>3) ඇත, ඒ සෑම එකක්ම දෙකක් ඇත x,y අගයන්- ඛණ්ඩාංක පික්සල් වලින් සහ ඛණ්ඩාංක මීටර් වලින්.
පික්සෙල් වල ඛණ්ඩාංක දැනගෙන මීටර වලින් අතරමැදි ඛණ්ඩාංක අගයන් සොයා ගැනීම අවශ්‍ය වේ.
රේඛීය මැදිහත්වීම සුදුසු නොවේ - රේඛාවෙන් පිටත දෝෂය ඉතා විශාලය.
මේ වගේ: (Xc යනු ගවයා දිගේ මීටරවල ඛණ්ඩාංකය, Xp යනු ගවයා දිගේ පික්සල්වල ඛණ්ඩාංකය, Xc3 යනු ගවයාගේ අපේක්ෂිත අගයයි)
Xc3= (Xc1-Xc2)/(Xp1-Xp2)*(Xp3-Xp2)+Xc2
Yc3= (Yc1-Yc2)/(Yp1-Yp2)*(Yp3-Yp2)+Yc2

Xc සහ Yc සොයා ගැනීම සඳහා එකම සූත්‍රය සොයා ගන්නේ කෙසේද, දෙකක් (මෙහි මෙන්), නමුත් දන්නා යොමු ලකුණු N සැලකිල්ලට ගනිමින්?

Joka fern lowd

ලිඛිත සූත්‍ර අනුව විනිශ්චය කිරීම, පික්සල් සහ මීටරවල ඛණ්ඩාංක පද්ධතිවල අක්ෂ සමපාත වේද?
එනම් Xp -> Xc ස්වාධීනව සහ Yp -> Yc ස්වාධීනව අන්තර් සම්බන්ධිත වේ. එසේ නොවේ නම්, ඔබ Xp,Yp->Xc සහ Xp,Yp->Yc යන ද්විමාන මැදිහත්වීම භාවිතා කළ යුතුය, එය කාර්යය තරමක් සංකීර්ණ කරයි.
Xp සහ Xc ඛණ්ඩාංක යම් යැපීමකින් සම්බන්ධ වන බව තවදුරටත් උපකල්පනය කෙරේ.
රඳා පැවැත්මේ ස්වභාවය දන්නේ නම් (හෝ උපකල්පනය කරන්නේ නම්, උදාහරණයක් ලෙස, අපි උපකල්පනය කරන්නේ Xc=a*Xp^2+b*Xp+c), එවිට අපට මෙම පරායත්තතාවයේ පරාමිතීන් ලබා ගත හැක (දී ඇති යැපීම සඳහා a, b, c) භාවිතා කිරීම විශ්ලේෂණය(ක්රමය අවම වශයෙන් වර්ග) . මෙම ක්‍රමයේදී, ඔබ යම් පරායත්තතාවයක් Xc(Xp) සඳහන් කරන්නේ නම්, ඔබට යොමු දත්ත මත යැපීමෙහි පරාමිතීන් සඳහා සූත්‍රයක් ලබා ගත හැක. මෙම ක්රමය, විශේෂයෙන්ම, සොයා ගැනීමට සහ රේඛීය යැපීම, හොඳම මාර්ගයලබා දී ඇති දත්ත කට්ටලය තෘප්තිමත් කිරීම.
අවාසිය: මෙම ක්‍රමයේදී, Xp පාලන ලක්ෂ්‍යවල දත්ත වලින් ලබාගත් Xc ඛණ්ඩාංක නිශ්චිත ඒවාට වඩා වෙනස් විය හැක. උදාහරණයක් ලෙස, පර්යේෂණාත්මක ලක්ෂ්‍ය හරහා අඳින ලද ආසන්න සරල රේඛාවක් මෙම ලක්ෂ්‍ය හරහා හරියටම ගමන් නොකරයි.
නිශ්චිත ලිපි හුවමාරුවක් අවශ්‍ය නම් සහ රඳා පැවැත්මේ ස්වභාවය නොදන්නා නම්, අන්තර් ක්‍රම භාවිතා කළ යුතුය. සරලම ගණිතමය වන්නේ Lagrange interpolation polynomial වන අතර එය හරියටම යොමු ලක්ෂ්‍ය හරහා ගමන් කරයි. කෙසේ වෙතත්, මෙම බහුපදයේ ඉහළ මට්ටම හේතුවෙන් විශාල සංඛ්යාවක්යොමු ලකුණු සහ දුර්වල අන්තර් සම්බන්ධක ගුණාත්මක භාවය, එය භාවිතා නොකිරීමට වඩා හොඳය. වාසිය සාපේක්ෂ සරල සූත්රයයි.
spline interpolation භාවිතා කිරීම වඩා හොඳය. මෙම ක්‍රමයේ සාරය නම්, අසල්වැසි ලක්ෂ්‍ය දෙකක් අතර එක් එක් කොටසෙහි, අධ්‍යයනය යටතේ යැපීම බහුපදයක් මගින් අන්තර් ඛණ්ඩනය කර ඇති අතර, විරාම දෙකෙහි එක්වන ස්ථානවල සුමට තත්ත්වයන් ලියා ඇත. මෙම ක්‍රමයේ ඇති වාසිය නම් අන්තර් ක්‍රියාකාරිත්වයේ ගුණාත්මක භාවයයි. අවාසි - ඉවත් කිරීම පාහේ කළ නොහැක්කකි සාමාන්ය සූත්රය, ඔබ එක් එක් කොටසෙහි බහුපදයේ සංගුණක ඇල්ගොරිතමය සොයා ගත යුතුය. තවත් අවාසියක් නම් ද්විමාන අන්තර් බන්ධනයට සාමාන්‍යකරණය කිරීමේ දුෂ්කරතාවයයි.

මෙය Bill Jelen ගේ පොතේ පරිච්ඡේදයකි.

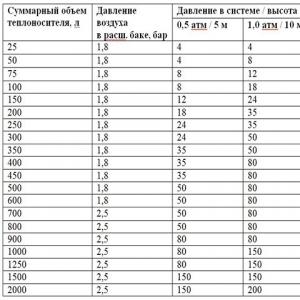
අභියෝගය: සමහර ඉංජිනේරු සැලසුම් ගැටළු පරාමිති අගයන් ගණනය කිරීම සඳහා වගු භාවිතා කිරීම අවශ්ය වේ. වගු විවික්ත බැවින්, නිර්මාණකරු අතරමැදි පරාමිති අගයක් ලබා ගැනීම සඳහා රේඛීය මැදිහත්වීම භාවිතා කරයි. වගුව (රූපය 1) බිමට ඉහලින් උස (පාලන පරාමිතිය) සහ සුළං වේගය (ගණනය කළ පරාමිතිය) ඇතුළත් වේ. උදාහරණයක් ලෙස, ඔබට මීටර් 47 ක උසකට අනුරූප වන සුළං වේගය සොයා ගැනීමට අවශ්ය නම්, ඔබ සූත්රය යෙදිය යුතුය: 130 + (180 - 130) * 7 / (50 - 40) = 165 m / sec.

සටහන හෝ ආකෘතියෙන් බාගන්න, ආකෘතියෙන් උදාහරණ

පාලන පරාමිතීන් දෙකක් තිබේ නම් කුමක් කළ යුතුද? එක් සූත්‍රයක් භාවිතයෙන් ගණනය කිරීම් සිදු කළ හැකිද? වගුව (රූපය 2) විවිධ උස සහ ව්‍යුහයන් සඳහා සුළං පීඩන අගයන් පෙන්වයි. මීටර් 25 ක උසකින් සහ මීටර් 300 ක පරාසයක සුළං පීඩනය ගණනය කිරීම අවශ්ය වේ.

විසඳුම: එක් පාලන පරාමිතියක් සමඟ නඩුව සඳහා භාවිතා කරන ක්රමය දීර්ඝ කිරීමෙන් අපි ගැටළුව විසඳන්නෙමු. මෙම පියවර අනුගමනය කරන්න:

රූපයේ දැක්වෙන වගුව සමඟ ආරම්භ කරන්න. 2. පිළිවෙලින් J1 සහ J2 හි උස සහ පරතරය සඳහා මූලාශ්‍ර සෛල එකතු කරන්න (රූපය 3).

සහල්. 3. සෛලවල ඇති සූත්‍ර J3:J17 මෙගාසූත්‍රයේ ක්‍රියාකාරිත්වය පැහැදිලි කරයි

සූත්‍ර භාවිතයේ පහසුව සඳහා නම් නිර්වචනය කරන්න (රූපය 4).

J3 කොටුවේ සිට J17 කොටුවට අනුක්‍රමිකව ගමන් කිරීමෙන් සූත්‍රය ක්‍රියා කරන ආකාරය නරඹන්න.

මෙගාසූත්‍රය තැනීමට ප්‍රතිලෝම අනුක්‍රමික ආදේශනය භාවිතා කරන්න. කොටුව J17 සිට J19 දක්වා සූත්‍ර පෙළ පිටපත් කරන්න. සූත්‍රයේ J15 වෙත යොමු කිරීම J15 කොටුවේ අගය සමඟ ප්‍රතිස්ථාපනය කරන්න: J7+(J8-J7)*J11/J13. සහ යනාදි. මෙහි ප්‍රතිඵලය වන්නේ අක්ෂර 984 කින් සමන්විත සූත්‍රයක් වන අතර එය මෙම ආකෘතියෙන් වටහා ගත නොහැක. අමුණා ඇති Excel ගොනුවේ ඔබට එය බැලිය හැක. මෙවැනි මෙගා සූත්‍රයක් භාවිතා කිරීමට ප්‍රයෝජනවත් දැයි මට විශ්වාස නැත.

සාරාංශය: වගු අගයන් පරාසයේ මායිම් සඳහා පමණක් නියම කර ඇත්නම් අතරමැදි පරාමිති අගයක් ලබා ගැනීම සඳහා රේඛීය මැදිහත්වීම භාවිතා කරයි; පාලන පරාමිතීන් දෙකක් භාවිතා කරමින් ගණනය කිරීමේ ක්රමයක් යෝජනා කෙරේ.

ඔබට පිටතින් ශ්‍රිත ගණනය කිරීමේ ප්‍රතිඵල දැන ගැනීමට අවශ්‍ය අවස්ථා තිබේ දන්නා ප්රදේශය. විශේෂයෙන් අදාළ වේ මෙම ප්රශ්නයඅනාවැකි ක්රියා පටිපාටිය සඳහා. Excel හි ඔබට මෙම මෙහෙයුම සිදු කළ හැකි ක්රම කිහිපයක් තිබේ. විශේෂිත උදාහරණ සමඟ ඒවා දෙස බලමු.

ක්රමය 2: ප්රස්ථාරය සඳහා නිස්සාරණය

ප්‍රවනතා රේඛාවක් සැලසුම් කිරීමෙන් ඔබට ප්‍රස්ථාරයක් සඳහා එක්ස්ට්‍රොපොලේෂන් ක්‍රියා පටිපාටියක් සිදු කළ හැකිය.

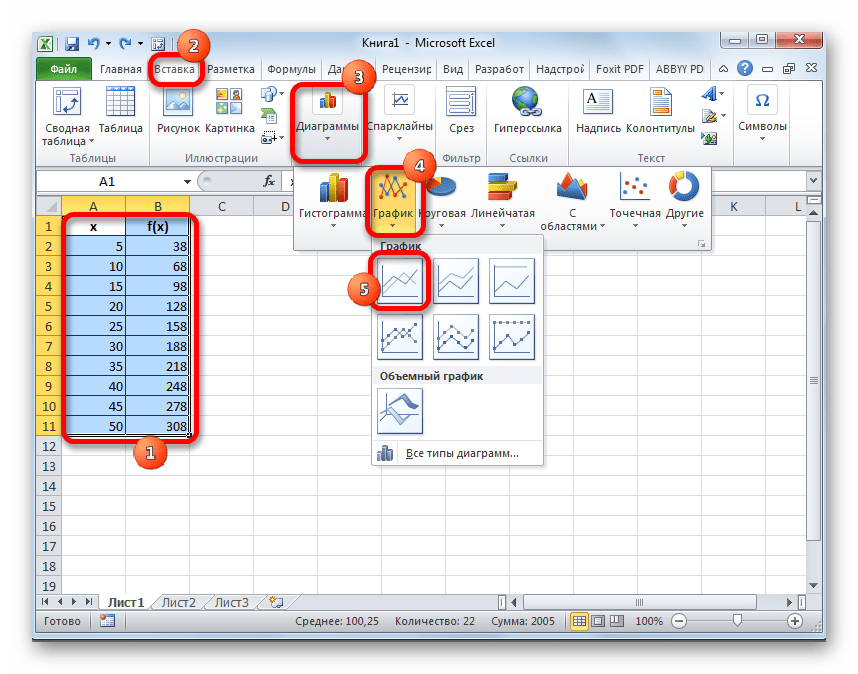
1. පළමුවෙන්ම, අපි ප්‍රස්ථාරයම ගොඩනඟමු. මෙය සිදු කිරීම සඳහා, තර්ක සහ අනුරූප ශ්‍රිත අගයන් ඇතුළුව, වගුවේ සම්පූර්ණ ප්‍රදේශය තේරීමට වම් මූසික බොත්තම තද කර ගනිමින් කර්සරය භාවිතා කරන්න. ඉන්පසුව, ටැබ් එකට ගමන් කරන්න "ඇතුළු කරන්න", බොත්තම මත ක්ලික් කරන්න "කාලසටහන". මෙම නිරූපකය බ්ලොක් එකේ පිහිටා ඇත "රූප සටහන්"මෙවලම් පටිය මත. ලැයිස්තුවක් දිස්වේ පවතින විකල්පප්රස්තාර. අපි අපගේ අභිමතය පරිදි වඩාත් සුදුසු එකක් තෝරා ගනිමු.



2. ප්‍රස්ථාරය ගොඩනැගීමෙන් පසු, එය තෝරා බොත්තම මත ක්ලික් කිරීමෙන් අමතර තර්ක රේඛාව ඉවත් කරන්න මකන්නපරිගණක යතුරු පුවරුව මත.



3. ඊළඟට, අපට අවශ්‍ය පරිදි තර්කවල අගයන් නොපෙන්වන බැවින්, තිරස් පරිමාණයේ බෙදීම් වෙනස් කළ යුතුය. මෙය සිදු කිරීම සඳහා, රූප සටහන මත දකුණු-ක්ලික් කරන්න සහ දිස්වන ලැයිස්තුවේ, අගය තෝරන්න "දත්ත තෝරන්න".



4. විවෘත වන දත්ත මූලාශ්ර තේරීමේ කවුළුවෙහි, බොත්තම මත ක්ලික් කරන්න "වෙනස් කරන්න"තිරස් අක්ෂ ලේබල් සංස්කරණ කොටසෙහි.



5. අක්ෂ අත්සන සැකසීම සඳහා කවුළුව විවෘත වේ. මෙම කවුළුවේ ක්ෂේත්රයේ කර්සරය තබන්න, ඉන්පසු තීරුවේ ඇති සියලුම දත්ත තෝරන්න "X"එහි නම නොමැතිව. ඉන්පසු බොත්තම මත ක්ලික් කරන්න "හරි".



6. දත්ත මූලාශ්ර තේරීමේ කවුළුව වෙත ආපසු යාමෙන් පසුව, අපි එම ක්රියා පටිපාටිය නැවත නැවතත්, එනම්, බොත්තම මත ක්ලික් කරන්න "හරි".



7. දැන් අපගේ ප්‍රස්ථාරය සකස් කර ඇති අතර අපට කෙලින්ම ප්‍රවණතා රේඛාවක් ගොඩනැගීමට පටන් ගත හැකිය. ප්‍රස්ථාරය මත ක්ලික් කරන්න, ඉන්පසු පීත්ත පටිය මත අමතර ටැබ් කට්ටලයක් සක්‍රිය වනු ඇත - "රූප සටහන් සමඟ වැඩ කිරීම". ටැබ් එක වෙත ගමන් කිරීම "පිරිසැලසුම"සහ බොත්තම ඔබන්න "ප්රවණතා රේඛාව"බ්ලොක් එකේ "විශ්ලේෂණය". අයිතමය මත ක්ලික් කරන්න "රේඛීය ආසන්න කිරීම"හෝ "ඝාතීය ආසන්නකරණය".



8. ප්‍රවනතා රේඛාව එකතු කර ඇත, නමුත් එය නැඹුරු විය යුතු තර්කයේ අගය අප විසින් නිශ්චිතව දක්වා නොමැති බැවින් එය ප්‍රස්ථාරයේම රේඛාවට සම්පූර්ණයෙන්ම පහළින් ඇත. මෙය සිදු කිරීම සඳහා, නැවත බොත්තම මත ක්ලික් කරන්න. "ප්රවණතා රේඛාව", නමුත් දැන් අයිතමය තෝරන්න "උසස් ප්රවණතා විකල්ප".



9. ප්‍රවණතා ආකෘති කවුළුව විවෘත වේ. පරිච්ඡේදයේ "Trend Line විකල්ප"සැකසුම් අවහිරයක් ඇත "අනාවැකිය". පෙර ක්‍රමයේදී මෙන්, අපි Extrapolation සඳහා තර්කය ගනිමු 55 . අපට පෙනෙන පරිදි, මෙතෙක් ප්‍රස්ථාරයට තර්කය දක්වා දිගක් ඇත 50 ඇතුළුව. අපි එය තවත් කෙනෙකුට දීර්ඝ කිරීමට අවශ්ය බව හැරෙනවා 5 ඒකක. තිරස් අක්ෂයේ ඒකක 5ක් එක බෙදීමක් සමාන වන බව ඔබට පෙනේ. එබැවින් මෙය එක් කාල පරිච්ඡේදයකි. ක්ෂේත්රයේ "ඉදිරියට"අගය ඇතුලත් කරන්න "1". බොත්තම මත ක්ලික් කරන්න "වසන්න"කවුළුවේ පහළ දකුණු කෙළවරේ.



10. ඔබට පෙනෙන පරිදි, කාලසටහන දිගු කර ඇත නිශ්චිත දිගනැඹුරු රේඛාවක් භාවිතා කිරීම.

ඉතින්, අපි වගු සහ ප්‍රස්ථාර සඳහා Extrapolation හි සරලම උදාහරණ දෙස බැලුවෙමු. පළමු අවස්ථාවේ දී, කාර්යය භාවිතා වේ අනාවැකිය, සහ දෙවන - ප්රවණතා රේඛාවක්. නමුත් මෙම උදාහරණ මත පදනම්ව, ඔබට තවත් බොහෝ දේ තීරණය කළ හැකිය සංකීර්ණ කාර්යයන්පුරෝකථනය කිරීම.

අපගෙන් බොහෝ දෙනෙකුට විවිධ විද්‍යාවන්හි තේරුම්ගත නොහැකි යෙදුම් හමු වී ඇත. නමුත් නොතේරෙන වචන වලට බිය නොවන අය ඉතා ස්වල්පයක් ඇත, නමුත් ඊට පටහැනිව, ඔවුන් ඔවුන්ව දිරිමත් කරන අතර ඔවුන් ඉගෙන ගන්නා විෂයයට ගැඹුරට යාමට බල කරති. අද අපි කතා කරන්නේ ඉන්ටර්පෝලේෂන් වැනි දෙයක් ගැන ය. මෙය දන්නා ලක්ෂ්‍ය භාවිතයෙන් ප්‍රස්ථාර තැනීමේ ක්‍රමයකි, ශ්‍රිතයක් පිළිබඳ අවම තොරතුරු ප්‍රමාණයක් සමඟ, වක්‍රයේ නිශ්චිත කොටස් මත එහි හැසිරීම පුරෝකථනය කිරීමට ඉඩ සලසයි.

නිර්වචනයේ සාරය වෙත යාමට පෙර සහ ඒ ගැන වඩාත් විස්තරාත්මකව කතා කිරීමට පෙර, අපි ඉතිහාසය ගැන ටිකක් ගැඹුරින් සොයා බලමු.

කතාව

පුරාණ කාලයේ සිට අන්තර් සම්බන්ධ කිරීම දන්නා කරුණකි. කෙසේ වෙතත්, මෙම සංසිද්ධිය අතීතයේ විශිෂ්ඨතම ගණිතඥයින් කිහිප දෙනෙකුට එහි වර්ධනයට ණයගැතියි: නිව්ටන්, ලයිබ්නිස් සහ ග්‍රෙගරි. එකල පැවති වඩාත් දියුණු ගණිත ශිල්පීය ක්‍රම භාවිතා කරමින් මෙම සංකල්පය ගොඩනැගුවේ ඔවුන්ය. මෙයට පෙර, මැදිහත්වීම, ඇත්ත වශයෙන්ම, ගණනය කිරීම් වලදී යොදන ලදී, නමුත් ඔවුන් එය කළේ සම්පූර්ණයෙන්ම සාවද්‍ය ක්‍රමවලට අනුව ය. විශාල ප්රමාණයක්යථාර්ථයට වඩා අඩු හෝ අඩු ආකෘතියක් ගොඩනැගීමට දත්ත.

අද අපට වඩාත් සුදුසු අන්තර් සම්බන්ධීකරණ ක්‍රමය පවා තෝරා ගත හැකිය. සෑම දෙයක්ම පරිගණක භාෂාවකට පරිවර්තනය කර ඇති අතර, එය ඉතා නිරවද්‍යතාවයකින් දන්නා ලකුණු වලින් සීමා වූ යම් ප්‍රදේශයක ශ්‍රිතයක හැසිරීම පුරෝකථනය කළ හැකිය.

අන්තර් හුවමාරුව තරමක් පටු සංකල්පයකි, එබැවින් එහි ඉතිහාසය කරුණු වලින් එතරම් පොහොසත් නොවේ. මීළඟ කොටසේදී, අපි අන්තර් ක්‍රියාකාරිත්වය යනු කුමක්ද සහ එය එහි ප්‍රතිවිරුද්ධ දෙයට වඩා වෙනස් වන්නේ කෙසේදැයි සොයා බලමු.

අන්තර් නිරෝධනය යනු කුමක්ද?

අප දැනටමත් පවසා ඇති පරිදි, ලකුණු අනුව ප්‍රස්ථාරයක් තැනීමට ඔබට ඉඩ සලසන ක්‍රම සඳහා පොදු නම මෙයයි. පාසැලේදී, මෙය ප්‍රධාන වශයෙන් සිදු කරනුයේ මේසයක් ඇඳීම, ප්‍රස්ථාරයක ලකුණු හඳුනා ගැනීම සහ ඒවා සම්බන්ධ කරන රේඛා දළ වශයෙන් ඇඳීමෙනි. අවසාන ක්‍රියාව සිදු කරනු ලබන්නේ අධ්‍යයනයට ලක්ව ඇති ශ්‍රිතයේ අන්‍යයන්ට සමානත්වය, අප දන්නා ප්‍රස්ථාර වර්ගය සලකා බැලීම මත ය.

කෙසේ වෙතත්, ලක්ෂ්‍යයෙන් ලක්ෂ්‍ය ප්‍රස්ථාරයක් සැලසුම් කිරීමේ කාර්යය ඉටු කිරීම සඳහා වෙනත්, වඩාත් සංකීර්ණ සහ නිවැරදි ක්‍රම තිබේ. එබැවින්, අන්තර් සම්බන්ධනය යනු දන්නා ලක්ෂ්‍ය වලින් සීමා වූ නිශ්චිත ප්‍රදේශයක ශ්‍රිතයක හැසිරීම පිළිබඳ “අනාවැකි” වේ.

එකම ප්‍රදේශය හා සම්බන්ධ සමාන සංකල්පයක් ඇත - Extrapolation. එය ශ්‍රිතයක ප්‍රස්ථාරයේ පුරෝකථනයක් ද නියෝජනය කරයි, නමුත් ප්‍රස්ථාරයේ දන්නා ලකුණු වලින් ඔබ්බට. මෙම ක්‍රමය සමඟින්, දන්නා ප්‍රාන්තරයක ශ්‍රිතයක හැසිරීම මත පදනම්ව පුරෝකථනයක් සිදු කරනු ලබන අතර, පසුව මෙම ශ්‍රිතය නොදන්නා අන්තරයට යොදනු ලැබේ. සඳහා මෙම ක්රමය ඉතා පහසු වේ ප්රායෝගික යෙදුමසහ සක්‍රීයව භාවිතා කරයි, උදාහරණයක් ලෙස, වෙළඳපොලේ උච්චාවචනයන් පුරෝකථනය කිරීමට සහ අනාවැකි කිරීමට ආර්ථික විද්‍යාවේ ජනවිකාස තත්ත්වයරට තුල.

නමුත් අපි ප්‍රධාන මාතෘකාවෙන් ඈත් වෙලා. මීළඟ කොටසේදී, අපි මැදිහත්වීම සිදුවන්නේ කුමක්ද සහ මෙම මෙහෙයුම සිදු කිරීමට භාවිතා කළ හැකි සූත්‍ර මොනවාදැයි සොයා බලමු.

මැදිහත්වීම් වර්ග

වඩාත් සරල දසුනක්යනු ආසන්නතම අසල්වැසි ක්‍රමය භාවිතා කරමින් අන්තර් ක්‍රියා කිරීමයි. මෙම ක්රමය භාවිතා කරමින්, අපි සෘජුකෝණාස්රාකාර වලින් සමන්විත ඉතා රළු ප්රස්ථාරයක් ලබා ගනිමු. ප්‍රස්ථාරයක අනුකලයක ජ්‍යාමිතික අර්ථය පැහැදිලි කිරීමක් ඔබ කවදා හෝ දැක ඇත්නම්, අප කතා කරන්නේ කුමන ආකාරයේ චිත්‍රක ස්වරූපයක් දැයි ඔබට වැටහෙනු ඇත.

මීට අමතරව, වෙනත් අන්තර් සම්බන්ධක ක්රම තිබේ. වඩාත් ප්රසිද්ධ හා ජනප්රිය බහුපද සම්බන්ධ වේ. ඒවා වඩාත් නිවැරදි වන අතර තරමක් සොච්චම් අගයන් සමඟ ශ්‍රිතයක හැසිරීම පුරෝකථනය කිරීමට ඔබට ඉඩ සලසයි. අපි බලමු පළමු අන්තර් ඡේදනය කිරීමේ ක්‍රමය රේඛීය බහුපද අන්තර් ඡේදනයයි. මෙම කාණ්ඩයේ ඇති සරලම ක්‍රමය මෙය වන අතර, ඔබ සෑම කෙනෙකුම එය පාසලේදී භාවිතා කළ හැකිය. එහි සාරය නම් දන්නා ලක්ෂ්ය අතර සරල රේඛා ගොඩනැගීමයි. ඔබ දන්නා පරිදි, තනි සරල රේඛාවක් තලයක ලක්ෂ්‍ය දෙකක් හරහා ගමන් කරයි, මෙම ලක්ෂ්‍යවල ඛණ්ඩාංක මත පදනම්ව එහි සමීකරණය සොයාගත හැකිය. මෙම සරල රේඛා තැනීමෙන් පසු, අපට කැඩුණු ප්‍රස්ථාරයක් ලැබේ, එය අවම වශයෙන්, නමුත් ශ්‍රිතවල ආසන්න අගයන් පිළිබිඹු කරයි. සාමාන්ය දළ සටහනයථාර්ථයට ගැලපේ. රේඛීය මැදිහත්වීම සිදු කරනු ලබන්නේ එලෙස ය.

උසස් ආකාරයේ මැදිහත්වීම්

වඩා රසවත් එකක් ඇත, නමුත් ඒ සමඟම තවත් දුෂ්කර මාර්ගයමැදිහත් වීම. එය සොයාගනු ලැබුවේ ප්‍රංශ ගණිතඥ ජෝසප් ලුවී ලග්රංගේ විසිනි. මෙම ක්‍රමය භාවිතා කරමින් අන්තර් ක්‍රියාකාරිත්වය ගණනය කිරීම එහි නමින් නම් කර ඇත්තේ එබැවිනි: ලැග්‍රේන්ජ් ක්‍රමය භාවිතයෙන් අන්තර් ක්‍රියා කිරීම. මෙහි උපක්‍රමය මෙයයි: පෙර ඡේදයේ දක්වා ඇති ක්‍රමය භාවිතා කරන්නේ නම් පමණි රේඛීය ශ්රිතය, පසුව Lagrange ක්‍රමය මගින් ප්‍රසාරණය කිරීම සඳහා ඉහළ උපාධිවල බහුපද භාවිතය ද ඇතුළත් වේ. නමුත් විවිධ ක්‍රියාවන් සඳහා අන්තර් ක්‍රියා සූත්‍ර සොයා ගැනීම එතරම් පහසු නැත. තවද කරුණු වැඩි ප්‍රමාණයක් දන්නා තරමට, අන්තර් ක්‍රියා සූත්‍රය වඩාත් නිවැරදි වේ. නමුත් තවත් බොහෝ ක්රම තිබේ.

යථාර්ථයට සමීප වන වඩාත් දියුණු ගණනය කිරීමේ ක්රමයක් තිබේ. එහි භාවිතා වන අන්තර් ධ්‍රැව සූත්‍රය බහුපද සමූහයකි, ඒ එක් එක් යෙදුම ශ්‍රිතයේ කොටස මත රඳා පවතී. මෙම ක්රමය spline ශ්රිතයක් ලෙස හැඳින්වේ. මීට අමතරව, විචල්‍ය දෙකක අන්තර් පොලේට් ශ්‍රිත වැනි දෙයක් කිරීමට ක්‍රම ද තිබේ. ඇත්තේ ක්රම දෙකක් පමණි. ඒවා අතර ද්විපාර්ශ්වික හෝ ද්විත්ව මැදිහත්වීම වේ. මෙම ක්‍රමය මඟින් ඔබට ත්‍රිමාණ අවකාශයේ ලක්ෂ්‍ය භාවිතයෙන් ප්‍රස්ථාරයක් පහසුවෙන් ගොඩනගා ගත හැක. අපි වෙනත් ක්රම ස්පර්ශ නොකරමු. සාමාන්‍යයෙන්, ප්‍රස්ථාර තැනීමේ මෙම සියලු ක්‍රම සඳහා අන්තර් ක්‍රියාකාරිත්වය යනු විශ්වීය නමකි, නමුත් මෙම ක්‍රියාව සිදු කළ හැකි විවිධ ක්‍රම මෙම ක්‍රියාවට යටත් වන ශ්‍රිතයේ වර්ගය අනුව ඒවා කණ්ඩායම් වලට බෙදීමට අපට බල කරයි. එනම්, අප ඉහතින් බැලූ උදාහරණයක් වන ඉන්ටර්පෝලේෂන් සෘජු ක්‍රමවලට යොමු වේ. ප්‍රතිලෝම මැදිහත්වීමක් ද ඇත, එය වෙනස් වන්නේ එය සෘජු ලෙස නොව ගණනය කිරීමට ඉඩ සලසයි ප්රතිලෝම ශ්රිතය(එනම්, y සිට x). එය තරමක් සංකීර්ණ වන අතර හොඳ ගණිතමය දැනුමක් අවශ්‍ය බැවින් අපි අවසාන විකල්ප සලකා බලන්නේ නැත.

අපි සමහර විට වඩාත් වැදගත් කොටස් වලින් එකකට යමු. අප සාකච්ඡා කරන ක්‍රම මාලාව ජීවිතයට අදාළ වන්නේ කෙසේද සහ කොතැනද යන්න එයින් අපි ඉගෙන ගනිමු.

අයදුම්පත

අපි දන්නා පරිදි ගණිතය යනු විද්‍යාවේ රැජිනයි. එමනිසා, මුලදී ඔබ ඇතැම් මෙහෙයුම්වල කාරණය නොපෙනුනත්, ඒවා නිෂ්ඵල බව මින් අදහස් නොවේ. උදාහරණයක් ලෙස, දැන් ස්වල්ප දෙනෙකුට අවශ්‍ය වන ප්‍රස්ථාර පමණක් ගොඩනගා ගත හැකි මැදිහත්වීම නිෂ්ඵල දෙයක් බව පෙනේ. කෙසේ වෙතත්, තාක්‍ෂණය, භෞතික විද්‍යාව සහ වෙනත් බොහෝ විද්‍යාවන්හි (උදාහරණයක් ලෙස, ජීව විද්‍යාව) ඕනෑම ගණනය කිරීම් සඳහා, නිශ්චිත අගයන් සමූහයක් ඇති අතරම, සංසිද්ධිය පිළිබඳ තරමක් සම්පූර්ණ චිත්‍රයක් ඉදිරිපත් කිරීම අතිශයින් වැදගත් වේ. ප්‍රස්ථාරය පුරා විසිරී ඇති අගයන් සෑම විටම නිශ්චිත ප්‍රදේශයක ශ්‍රිතයේ හැසිරීම, එහි ව්‍යුත්පන්නවල අගයන් සහ අක්ෂ සමඟ ඡේදනය වන ස්ථාන පිළිබඳ පැහැදිලි අදහසක් ලබා නොදේ. තවද මෙය අපගේ ජීවිතයේ බොහෝ අංශ සඳහා ඉතා වැදගත් වේ.

මෙය ජීවිතයට ප්‍රයෝජනවත් වන්නේ කෙසේද?

මෙවැනි ප්‍රශ්නයකට පිළිතුරු දීමට ඉතා අපහසු විය හැක. නමුත් පිළිතුර සරලයි: ක්රමයක් නැත. මෙම දැනුම ඔබට කිසිදු ප්‍රයෝජනයක් නොවනු ඇත. නමුත් ඔබ මෙම ද්රව්යය සහ මෙම ක්රියාවන් සිදු කරන ක්රම තේරුම් ගන්නේ නම්, ඔබ ඔබේ තර්කනය පුහුණු කරනු ඇත, එය ජීවිතයේ ඉතා ප්රයෝජනවත් වනු ඇත. ප්රධාන දෙය වන්නේ දැනුමම නොවේ, නමුත් අධ්යයන ක්රියාවලියේදී පුද්ගලයෙකු ලබා ගන්නා කුසලතා. "සදහටම ජීවත් වන්න, සදහටම ඉගෙන ගන්න" යන කියමනක් තිබීම නිකම්ම නොවේ.

අදාළ සංකල්ප

මෙම ගණිත ක්ෂේත්‍රය කෙතරම් වැදගත්ද යන්න (තවමත්) ඔබටම තේරුම් ගත හැක්කේ ඒ හා සම්බන්ධ අනෙකුත් විවිධ සංකල්ප දෙස බැලීමෙන්. අපි දැනටමත් Extrapolation ගැන කතා කර ඇත, නමුත් දළ වශයෙන් ද ඇත. සමහරවිට ඔබ දැනටමත් මෙම වචනය අසා ඇති. ඕනෑම අවස්ථාවක, අපි මෙම ලිපියෙන් එහි තේරුම ගැන ද සාකච්ඡා කළෙමු. ආසන්න කිරීම, අන්තර් ක්‍රියාකාරිත්වය වැනි, ශ්‍රිතවල ප්‍රස්ථාර ගොඩනැගීමට සම්බන්ධ සංකල්ප වේ. නමුත් පළමු සහ දෙවන අතර වෙනස වන්නේ එය සමාන දන්නා ප්‍රස්ථාර මත පදනම් වූ ප්‍රස්ථාරයක ආසන්න ඉදිකිරීමකි. මෙම සංකල්ප දෙක එකිනෙකට බෙහෙවින් සමාන වන අතර, ඒ සෑම එකක්ම අධ්යයනය කිරීම වඩාත් රසවත් කරයි.

නිගමනය

ගණිතය යනු බැලූ බැල්මට පෙනෙන තරම් සංකීර්ණ විද්‍යාවක් නොවේ. ඇය තරමක් සිත්ගන්නා සුළුය. මෙම ලිපියෙන් අපි එය ඔබට ඔප්පු කිරීමට උත්සාහ කළෙමු. අපි කුමන්ත්‍රණයට අදාළ සංකල්ප දෙස බැලුවෙමු, ද්විත්ව මැදිහත්වීම යනු කුමක්දැයි ඉගෙන ගත් අතර එය භාවිතා කරන උදාහරණ දෙස බැලුවෙමු.