Функція називається спадною на проміжку. Достатні ознаки зростання та зменшення функції

Монотонність

Дуже важливою властивістю функції є монотонність. Знаючи цю властивість різних спеціальних функцій, можна визначити поведінку різних фізичних, економічних, соціальних та багатьох інших процесів.

Виділяють наступні видимонотонності функцій:

1) функція зростаєякщо на деякому інтервалі, якщо для будь-яких двох точок і цього інтервалу таких, що виконано, що . Тобто. більшого значення аргументу відповідає більше значення функції;

2) функція зменшуєтьсяякщо на деякому інтервалі, якщо для будь-яких двох точок і цього інтервалу таких, що виконано, що . Тобто. більшого значення аргументу відповідає менше значення функції;

3) функція невпадаєякщо на деякому інтервалі, якщо для будь-яких двох точок і цього інтервалу таких, що виконано, що ;

4) функція не зростаєякщо на деякому інтервалі, якщо для будь-яких двох точок і цього інтервалу таких, що виконано, що .

2. Для перших двох випадків ще застосовують термін "сувора монотонність".

3. Два останні випадки є специфічними і зазвичай задаються у вигляді композиції з декількох функцій.

4. Окремо зазначимо, що розглядати зростання та спадання графіка функції слід саме ліворуч-право і ніяк інакше.

2. Парність/непарність.

Функція називається непарноюякщо при зміні знака аргументу, вона змінює своє значення на протилежне. Формульний запис цього виглядає так . Це означає, що після підстановки на місце всіх іксів значень «мінус ікс», функція змінить свій знак. Графік такої функції симетричний щодо початку координат.

Прикладами непарних функцій є та інших.

Наприклад, графік дійсно має симетричність щодо початку координат:

Функція називається парноюЯкщо зміна символу аргументу, вона не змінює значення. Формульний запис цього виглядає так. Це означає, що після підстановки на місце всіх іксів значень «мінус ікс», функція в результаті не зміниться. Графік такої функції симетричний щодо осі.

Прикладами парних функцій є та інших.

Наприклад, покажемо симетричність графіка щодо осі:

Якщо функція не відноситься до жодного із зазначених видів, то її називають ні парною ні непарною або функцією загального вигляду . Такі функції не мають симетрії.

Такою функцією, наприклад, є нещодавно розглянута нами лінійна функціяз графіком:

3. Особливою властивістюфункцій є періодичність.

Справа в тому, що періодичними функціями, які розглядаються у стандартній шкільній програмі, є лише тригонометричні функції. Ми вже детально про них говорили щодо відповідної теми.

Періодична функція– це функція, яка змінює значення при додаванні до аргументу певного постійного ненульового числа.

Таке мінімальне число називають періодом функціїі позначають літерою.

Формульний запис цього виглядає так: .

Подивимося цю властивість з прикладу графіка синуса:

Згадаємо, що періодом функцій і є , а періодом і – .

Як ми вже знаємо, для тригонометричних функційзі складним аргументомможливо нестандартний період. Йдеться про функції виду:

У них період дорівнює. І про функції:

У них період дорівнює.

Як бачимо, для обчислення нового періоду стандартний період ділиться на множник при аргументі. Від інших видозмін функції він не залежить.

Обмеженість.

функцію y=f(x) називають обмеженою знизу на множині Х⊂D(f), якщо існує таке число а, що для будь-яких хХ виконується нерівність f(x)< a.

функцію y=f(x) називають обмеженою зверху на множині Х⊂D(f), якщо існує таке число а, що для будь-яких хХХ виконується нерівність f(x)< a.

Якщо проміжок Х не вказується, то вважають, що функція обмежена по всій області визначення. Функція обмежена і згори, і знизу називається обмеженою.

Обмеженість функції легко читається за графіком. Можна провести деяку пряму у=а, і якщо функція вища за цю пряму, то обмеженість знизу.

Якщо нижче, відповідно зверху. Нижче наведено графік обмеженої знизу функції. Графік обмеженої функції, хлопці, спробуйте малювати самі.

Тема: Властивості функцій: проміжки зростання та спадання; найбільше та найменше значення; точки екстремуму (локального максимуму та мінімуму), опуклість функції.

Проміжки зростання та спадання.

На підставі достатніх умов (ознак) зростання та зменшення функції знаходяться проміжки зростання та зменшення функції.

Ось формулювання ознак зростання та зменшення функції на інтервалі:

· якщо похідна функції y=f(x)позитивна для будь-кого xз інтервалу X, то функція зростає на X;

· якщо похідна функції y=f(x)негативна для будь-якого xз інтервалу X, то функція зменшується на X.

Таким чином, щоб визначити проміжки зростання та зменшення функції необхідно:

· Визначити область визначення функції;

· Визначити похідну функції;

· Вирішити нерівності та на області визначення;

1. Знайти область визначення функції

2.Знайти похідну функції

3. Прирівняти похідну до нуля та знайти критичні точки функції

4. Відзначити критичні точки в області визначення

5. Обчислити знак похідної у кожному з отриманих інтервалів

6. З'ясувати поведінку функції у кожному інтервалі.

Приклад: Знайдіть проміжки зростання та зменшення функціїf(x) = і число нулів цієї функції на проміжку.

Рішення:

1. D( f) = R

2. f"(x) =

D( f") = D( f) = R

3. Знайдемо критичні точки функції, розв'язавши рівняння f"(x) = 0.

x(x – 10) = 0

критичні точки функції x= 0 і x = 10.

4. Визначимо знак похідної.

f"(x) + – +

f(x) 0 10x

у проміжках (-∞; 0) та (10; +∞) похідна функції позитивна і в точках x= 0 та x = 10 функція f(x) безперервна, отже, дана функція зростає на проміжках: (-∞; 0];

Визначимо знак значень функції кінцях відрізка.

f(0) = 3, f(0) > 0

f(10) = , f(10) < 0.

Так як на відрізку функція зменшується і знак значень функції змінюється, то цьому відрізку один нуль функції.

Відповідь: функція f(x) зростає на проміжках: (-∞; 0];

на проміжку функція має один нуль функції.

2. Точки екстремуму функції: точки максимуму та точки мінімуму. Необхідна та достатня умови існування екстремуму функції. Правило дослідження функції на екстремум .

Визначення 1:Точки, у яких похідна дорівнює нулю, називаються критичними чи стаціонарними.

Визначення 2. Точка називається точкою мінімуму (максимуму) функції , якщо значення функції у цій точці менше (більше) найближчих значень функції.

Слід мати на увазі, що максимум і мінімум даному випадкує локальними.

На рис. 1. зображені локальні максимумита мінімуми.

Максимум та мінімум функції об'єднані загальною назвою: екстремум функції.

Теорема 1.(Необхідна ознака існування екстремуму функції). Якщо функція, що диференціюється в точці, має в цій точці максимум або мінімум, то її похідна при звертається в нуль, .

Теорема 2.(Достатня ознака існування екстремуму функції). Якщо безперервна функція має похідну у всіх точках деякого інтервалу, що містить критичну точку (за винятком може бути самої цієї точки), і якщо похідна при переході аргументу зліва направо через критичну точку змінює знак із плюсу на мінус, то функція у цій точці має максимум, а при переході знака з мінуса на плюс – мінімум.

На підставі достатніх ознак знаходяться проміжки зростання та зменшення функції.

Ось формулювання ознак:

• якщо похідна функції y = f(x)позитивна для будь-кого xз інтервалу X, то функція зростає на X;
• якщо похідна функції y = f(x)негативна для будь-якого xз інтервалу X, то функція зменшується на X.

Таким чином, щоб визначити проміжки зростання та зменшення функції необхідно:

• знайти область визначення функції;

• знайти похідну функції;

• до отриманих проміжків додати граничні точки, в яких функція визначена і безперервна.

Розглянемо приклад для роз'яснення алгоритму.

приклад.

Знайти проміжки зростання та зменшення функції .

Рішення.

Першим кроком є ​​знаходження обросту визначення функції. У нашому прикладі вираз у знаменнику не повинен звертатися в нуль, отже, .

Переходимо до похідної функції:

Для визначення проміжків зростання та зменшення функції за достатньою ознакою розв'язуємо нерівності і в області визначення. Скористайтеся узагальненням методу інтервалів. Єдиним дійсним коренем чисельника є x = 2, а знаменник звертається в нуль при x = 0. Ці точки розбивають область визначення інтервали, у яких похідна функції зберігає знак. Зазначимо ці точки на числовій прямій. Плюсами та мінусами умовно позначимо інтервали, на яких похідна позитивна чи негативна. Стрілки знизу схематично показують зростання або зменшення функції на відповідному інтервалі.

Таким чином, і .

У точці x = 2функція визначена та безперервна, тому її слід додати і до проміжку зростання та до проміжку спадання. У точці x = 0функція не визначена, тому цю точку не включаємо в інтервали, що шукаються.

Наводимо графік функції зіставлення з нею отриманих результатів.

Відповідь:функція зростає при , зменшується на інтервалі (0; 2] .

- Точки екстремуму функції однієї змінної. Достатні умови екстремуму

Нехай функція f(x), визначена і безперервна в проміжку, не є монотонною. Знайдуться такі частини [ , ] проміжку , у яких максимальне і найменше значення досягається функцією у внутрішній точці, тобто. між в.

Кажуть, що функція f(x) має в точці максимум (або мінімум), якщо цю точку можна оточити такою околицею (x 0 - , x 0 +), що міститься в проміжку, де задана функція, що для всіх її точок виконується нерівність.

f(x)< f(x 0)(или f(x)>f(x 0))

Іншими словами, точка x 0 доставляє функції f(x) максимум (мінімум), якщо значення f(x 0) виявляється найбільшим (найменшим) із значень, що приймаються функцією в деякій (хоч би малій) околиці цієї точки. Зазначимо, що визначення максимуму (мінімуму) передбачає, що функція задана з обох боків від точки x 0 .

Якщо існує така околиця, в межах якої (при x = x 0) виконується сувора нерівність

f(x) f(x 0)

то кажуть, що функція має у точці x 0 власний максимум (мінімум), інакше – невласний.

Якщо функція має максимуми в точках x 0 і x 1 , то, застосовуючи до проміжку другу теорему Вейерштрасса, бачимо, що найменшого значення в цьому проміжку функція досягає в деякій точці x 2 між x 0 і x 1 і має там мінімум. Аналогічно між двома мінімумами неодмінно знайдеться максимум. У тому найпростішому (і практично – найважливішому) випадку, коли функція має лише кінцеве число максимумів і мінімумів, вони просто чергуються.

Зауважимо, що для позначення максимуму або мінімуму існує і термін, що їх об'єднує, – екстремум.

Поняття максимум (max f(x)) та мінімум (min f(x)) є локальними властивостями функції та мають місце у певній точці х 0 . Поняття найбільшого (sup f(x)) та найменшого (inf f(x)) значень відносяться до кінцевого відрізку та є глобальними властивостями функції на відрізку.

З малюнка 1 видно, що у точках х 1 і х 3 локальні максимуми, а точках х 2 і х 4 – локальні мінімуми. Проте, найменшого значенняфункція досягає у точці х = а, а найбільшого – у точці х = b.

Поставимо завдання про розшук всіх значень аргументу, що доставляють функції екстремуму. При вирішенні її основну роль гратиме похідна.

Припустимо спочатку, що з функції f(x) у проміжку(a,b) існує кінцева похідна. Якщо в точці х 0 функція має екстремум, то, застосовуючи до проміжку (х 0 - , Х 0 +), про яку була мова вище, теорему Ферма, укладаємо, що f(x) = 0 це полягає необхідна умова екстремуму. Екстремум слід шукати лише у тих точках, де похідна дорівнює нулю.

Не слід, думати, однак, що кожна точка, в якій похідна дорівнює нулю, доставляє функції екстремум: вказана щойно необхідна умова не є достатньою

Екстремуми функції

Визначення 2

Точка $x_0$ називається точкою максимуму функції $f(x)$, якщо є така околиця даної точки, що всім $x$ з цієї околиця виконується нерівність $f(x)\le f(x_0)$.

Визначення 3

Точка $x_0$ називається точкою максимуму функції $f(x)$, якщо є така околиця даної точки, що всім $x$ з цієї околиця виконується нерівність $f(x)\ge f(x_0)$.

Поняття екстремуму функції тісно пов'язані з поняттям критичної точки функції. Введемо її визначення.

Визначення 4

$x_0$ називається критичною точкоюфункції $f(x)$, якщо:

1) $x_0$ - внутрішня точка області визначення;

2) $f"\left(x_0\right)=0$ або немає.

Для поняття екстремуму можна сформулювати теореми про достатні та необхідні умови його існування.

Теорема 2

Достатня умоваекстремуму

Нехай точка $ x_0 $ є критичною для функції $ y = f (x) $ і лежить в інтервалі $ (a, b) $. Нехай кожному інтервалі $\left(a,x_0\right)\ і\ (x_0,b)$ похідна $f"(x)$ існує і зберігає постійний знак.

1) Якщо на інтервалі $(a,x_0)$ похідна $f"\left(x\right)>0$, а на інтервалі $(x_0,b)$ похідна $f"\left(x\right)

2) Якщо інтервалі $(a,x_0)$ похідна $f"\left(x\right)0$, то точка $x_0$ - точка мінімуму цієї функції.

3) Якщо і на інтервалі $(a,x_0)$, і на інтервалі $(x_0,b)$ похідна $f"\left(x\right) >0$ або похідна $f"\left(x\right)

Ця теорема проілюстрована малюнку 1.

Рисунок 1. Достатня умова існування екстремумів

Приклади екстремумів (рис. 2).

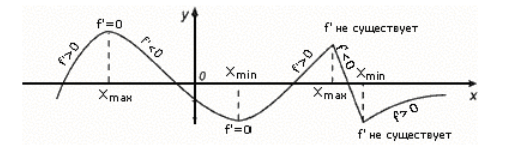
Рисунок 2. Приклади точок екстремумів

Правило дослідження функції на екстремум

2) Знайти похідну $f"(x)$;

7) Зробити висновки про наявність максимумів і мінімумів кожному проміжку, використовуючи теорему 2.

Зростання та зменшення функції

Введемо, для початку, визначення зростаючої та спадної функцій.

Визначення 5

Функція $y=f(x)$, визначена на проміжку $X$, називається зростаючою, якщо для будь-яких точок $x_1,x_2\in X$ при $x_1

Визначення 6

Функція $y=f(x)$, визначена на проміжку $X$, називається спадною, якщо для будь-яких точок $x_1,x_2\in X$ при $x_1f(x_2)$.

Дослідження функції на зростання та спадання

Дослідити функції на зростання та зменшення можна за допомогою похідної.

Для того щоб дослідити функцію на проміжки зростання та спадання, необхідно зробити наступне:

1) Знайти область визначення функції $ f (x) $;

2) Знайти похідну $f"(x)$;

3) Знайти точки, у яких виконується рівність $f"\left(x\right)=0$;

4) Знайти точки, де $f"(x)$ немає;

5) Відзначити на координатній прямій усі знайдені точки та область визначення цієї функції;

6) Визначити знак похідної $f"(x)$ на кожному проміжку, що вийшов;

7) Зробити висновок: на проміжках, де $f"\left(x\right)0$ функція зростає.

Приклади завдань на дослідження функцій на зростання, спад та наявність точок екстремумів

Приклад 1

Дослідити функцію на зростання і спадання, і наявність точок максимумів і мінімумів: $f(x)=(2x)^3-15x^2+36x+1$

Так як перші 6 пунктів збігаються, проведемо для початку їх.

1) Область визначення – всі дійсні числа;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $ f "\ left (x \ right) = 0 $;

\ \ \

4) $f"(x)$ існує у всіх точках області визначення;

5) Координатна пряма:

Малюнок 3.

6) Визначити знак похідної $f"(x)$ на кожному проміжку:

\ \.

Областю значень функції явл. проміжок [1; 3].

1. При x = -3, x = - 1, x = 1,5, х = 4,5 значення функції дорівнює нулю.

Значення аргументу, у якому значення функції дорівнює нулю, називають нулем функції.

//Тобто. для цієї функції числа -3; -1; 1,5; 4,5 є нулями.

2. На проміжках [4,5; 3) і (1; 1,5) і (4,5;5,5] графік функції f розташований над віссю абсцис, а на проміжках (-3; -1) та (1,5; 4,5) під віссю абсцис, це пояснюється так -на проміжках [4,5; 3) та (1; 1,5) та (4,5;5,5] функція приймає позитивні значення, а на проміжках (-3; -1) та (1,5; 4,5) негативні.

Кожен із зазначених проміжків (там де функція набуває значення одного й того ж знака) називають проміжком знаковості функції f.//тобто. наприклад, якщо взяти проміжок (0; 3), то він не є проміжком знакості цієї функції.

У математиці прийнято під час пошуку проміжків знаковості функції вказувати проміжки максимальної довжини. //Тобто. проміжок (2; 3) є проміжком знаковостіфункції f, але у відповідь слід увімкнути проміжок [4,5; 3), що містить проміжок (2; 3).

3. Якщо переміщатися по осі абсцис від 4,5 до 2, можна помітити, що графік функції йде вниз, тобто значення функції зменшуються. //У математиці прийнято говорити, що у проміжку [ 4,5; 2] функція зменшується.

Зі збільшенням x від 2 до 0 графік функції йде нагору, тобто. Значення функції збільшуються. //У математиці прийнято говорити, що у проміжку [ 2; 0] функція зростає.

Функцію f називають , якщо для будь-яких двох значень аргументу x1 і x2 з цього проміжку таких, що x2 > x1, виконується нерівність f(x2) > f(x1). // або функцію називають зростаючою на деякому проміжкуякщо для будь-яких значень аргументу з цього проміжку більшому значенню аргументу відповідає більше значення функції.//Тобто. що більше х, то більше в.

Функцію f називають спадаючою на деякому проміжкуякщо для будь-яких двох значень аргументу x1 і x2 з цього проміжку таких, що x2 > x1, виконується нерівність f(x2)зменшується на деякому проміжку, якщо для будь-яких значень аргументу з цього проміжку більшому значенню аргументу відповідає менше значення функції. //Тобто. що більше х, то менше у.

Якщо функція зростає по всій області визначення, її називають зростаючою.

Якщо функція зменшується по всій області визначення, її називають спадаючою.

приклад 1.графік зростаючої та спадної функцій відповідно.

приклад 2.

Визначити явл. чи лінійна функція f(x) = 3x + 5 зростаючою чи спадною?

Доведення. Відтворюємося визначеннями. Нехай х1 та x2 довільні значення аргументу, причому x1< x2., например х1=1, х2=7