අහඹු විචල්‍යයක ව්‍යාප්ති නියමය වන්නේ ගණිතමය අපේක්ෂාව සොයා ගැනීමයි. විවික්ත අහඹු විචල්යයන්. විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නීතිය
1 වන පරිච්ඡේදය. විවික්ත අහඹු අගය
§ 1. සසම්භාවී විචල්‍යයක සංකල්පය.
විවික්ත අහඹු විචල්‍යයක් බෙදා හැරීමේ නීතිය.
අර්ථ දැක්වීම : සසම්භාවී යනු පරීක්ෂණයේ ප්රතිඵලයක් ලෙස, කල්තියා නොදන්නා සහ අහඹු හේතූන් මත විය හැකි අගයන් සමූහයකින් එක් අගයක් පමණක් ගන්නා ප්‍රමාණයකි.
අහඹු විචල්‍ය වර්ග දෙකක් තිබේ: විවික්ත සහ අඛණ්ඩ.
අර්ථ දැක්වීම : සසම්භාවී විචල්යය X ලෙස හැඳින්වේ විවික්ත (අඛණ්ඩ) එහි අගයන් සමූහය පරිමිත හෝ අනන්ත නම්, නමුත් ගණන් කළ හැකි ය.
වෙනත් වචන වලින් කිවහොත්, විවික්ත අහඹු විචල්‍යයක විය හැකි අගයන් නැවත අංකනය කළ හැක.
ඔබට අහඹු විචල්‍යයක් එහි බෙදා හැරීමේ නියමය භාවිතයෙන් විස්තර කළ හැක.
අර්ථ දැක්වීම : විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නියමය සසම්භාවී විචල්‍යයක විය හැකි අගයන් සහ ඒවායේ සම්භාවිතාවන් අතර ලිපි හුවමාරුව ලෙස හැඳින්වේ.
විවික්ත සසම්භාවී විචල්‍ය X හි බෙදා හැරීමේ නියමය වගුවක ආකාරයෙන් ලබා දිය හැකි අතර, එහි පළමු පේළියේ සසම්භාවී විචල්‍යයේ හැකි සියලුම අගයන් ආරෝහණ අනුපිළිවෙලින් ද, දෙවන පේළියේ ඊට අනුරූප සම්භාවිතාවන් ද දක්වා ඇත. මෙම අගයන්, i.e.
එහිදී р1+ р2+…+ рn=1
එවැනි වගුවක් විවික්ත අහඹු විචල්‍යයක බෙදාහැරීමේ මාලාවක් ලෙස හැඳින්වේ.
අහඹු විචල්‍යයක විය හැකි අගයන් සමූහය අනන්ත නම්, р1+ р2+...+ рn+... ශ්‍රේණිය අභිසාරී වන අතර එහි එකතුව 1 ට සමාන වේ.
විවික්ත අහඹු විචල්‍ය X හි බෙදා හැරීමේ නියමය චිත්‍රක ලෙස නිරූපණය කළ හැක, ඒ සඳහා සෘජුකෝණාස්රාකාර පද්ධතියඛණ්ඩාංක, ඛණ්ඩාංක (xi;pi), i=1,2,...n සමඟ ලකුණු අනුපිළිවෙලින් සම්බන්ධ කරමින් බහු රේඛාවක් ගොඩනගා ඇත. ප්රතිඵලය රේඛාව ලෙස හැඳින්වේ බෙදාහැරීමේ බහුඅස්රය (රූපය 1).
කාබනික රසායන විද්‍යාව කාබනික රසායනයේ "href="/text/category/organicheskaya_hiimya/" rel="bookmark"> පිළිවෙලින් 0.7 සහ 0.8 වේ. සසම්භාවී විචල්‍ය X බෙදා හැරීමේ නීතිය අඳින්න - ශිෂ්‍යයා කරන විභාග ගණන සමත්.
විසඳුමක්. විභාගයේ ප්රතිඵලයක් ලෙස, සලකා බලන අහඹු විචල්‍ය X පහත අගයන්ගෙන් එකක් ගත හැක: x1=0, x2=1, x3=2.
මෙම අගයන්හි සම්භාවිතාව සොයා ගනිමු. සිදුවීම් දක්වන්න:
https://pandia.ru/text/78/455/images/image004_81.jpg" width="259" height="66 src=">
 |
එබැවින්, සසම්භාවී විචල්‍ය X හි බෙදා හැරීමේ නියමය වගුව මඟින් දක්වා ඇත:
පාලනය: 0.6+0.38+0.56=1.
§ 2. බෙදා හැරීමේ කාර්යය
සසම්භාවී විචල්‍යයක සම්පූර්ණ විස්තරයක් බෙදා හැරීමේ ශ්‍රිතය මගින් ද ලබා දේ.
අර්ථ දැක්වීම: විවික්ත අහඹු විචල්‍ය X හි බෙදා හැරීමේ ශ්‍රිතය F(x) ශ්‍රිතය හඳුන්වනු ලබන අතර, එය එක් එක් අගය සඳහා තීරණය කරයි x සසම්භාවී විචල්යය X x ට වඩා අඩු අගයක් ගන්නා සම්භාවිතාව:
F(x)=P(X<х)
ජ්යාමිතික වශයෙන්, බෙදා හැරීමේ ශ්‍රිතය සසම්භාවී විචල්‍ය X විසින් සංඛ්යා රේඛාවේ දැක්වෙන අගය x ලක්ෂ්‍යයේ වමට ඇති ලක්ෂ්‍යයකින් ලබා ගැනීමේ සම්භාවිතාව ලෙස අර්ථ දැක්වේ.
1)0≤F(x)≤1;
2) F(x) යනු (-∞;+∞) මත අඩු නොවන ශ්‍රිතයකි;
3) F(x) - x= xi (i=1,2,...n) ලක්ෂ්‍යවල වමේ සිට අඛණ්ඩව සහ අනෙකුත් සියලුම ලක්ෂ්‍යවල අඛණ්ඩව;
4) F(-∞)=P (X<-∞)=0 как вероятность невозможного события Х<-∞,
F(+∞)=P(X<+∞)=1 как вероятность достоверного события Х<-∞.
විවික්ත අහඹු විචල්‍ය X හි බෙදා හැරීමේ නියමය වගුවක ආකාරයෙන් ලබා දී ඇත්නම්:
එවිට බෙදා හැරීමේ ශ්‍රිතය F(x) සූත්රය මගින් තීරණය වේ:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110">
x≤ x1 සඳහා 0,
x1 හි p1< х≤ x2,
F(x)= p1 + p2 at x2< х≤ х3
x> xn සඳහා 1.
එහි ප්‍රස්ථාරය රූප සටහන 2 හි දැක්වේ:
§ 3. විවික්ත අහඹු විචල්‍යයක සංඛ්යාත්මක ලක්ෂණ.
වැදගත් සංඛ්යාත්මක ලක්ෂණ අතර වේ අපේක්ෂිත අගය.
අර්ථ දැක්වීම: ගණිතමය අපේක්ෂාව M(X) විවික්ත සසම්භාවී විචල්‍ය X යනු එහි සියලුම අගයන්හි නිෂ්පාදනවල එකතුව සහ ඒවාට අනුරූප සම්භාවිතාවයි:
M(X) = ∑ xiri= x1р1 + x2р2+…+ xnрn
ගණිතමය අපේක්ෂාව අහඹු විචල්‍යයක සාමාන්ය අගයේ ලක්ෂණයක් ලෙස ක්රියා කරයි.
ගණිතමය අපේක්ෂාවේ ගුණාංග:
1)M(C)=C, C යනු නියත අගයකි;
2) M (C X) \u003d C M (X),
3)M(X±Y)=M(X)±M(Y);
4)M(X Y)=M(X) M(Y), මෙහි X, Y යනු ස්වාධීන අහඹු විචල්‍ය වේ;
5)M(X±C)=M(X)±C, C යනු නියත අගයකි;
විවික්ත අහඹු විචල්‍යයක එහි මධ්‍යන්‍ය අගය වටා ඇති විය හැකි අගයන්ගේ විසරණයේ මට්ටම සංලක්ෂිත කිරීමට, විචලනය භාවිතා වේ.
අර්ථ දැක්වීම: විසුරුම ඩී ( x ) සසම්භාවී විචල්යය X යනු එහි ගණිතමය අපේක්ෂාවෙන් අහඹු විචල්‍යයේ වර්ග අපගමනයෙහි ගණිතමය අපේක්ෂාවයි:
විසර්ජන ගුණාංග:
1)D(C)=0, C යනු නියත අගයකි;
2)D(X)>0, X යනු අහඹු විචල්යයකි;
3)D(C X)=C2 D(X), මෙහි C යනු නියත අගයකි;
4)D(X+Y)=D(X)+D(Y), මෙහි X, Y යනු ස්වාධීන අහඹු විචල්‍ය වේ;
විචලනය ගණනය කිරීම සඳහා, සූත්රය භාවිතා කිරීම බොහෝ විට පහසුය:
D(X)=M(X2)-(M(X))2,
එහිදී М(Х)=∑ xi2рi= x12р1 + x22р2+…+ xn2рn
D(X) විචලනයට අහඹු විචල්‍යයක වර්ග මානය ඇත, එය සැමවිටම පහසු නොවේ. එබැවින්, අහඹු විචල්‍යයක විය හැකි අගයන් විසුරුවා හැරීමේ දර්ශකයක් ලෙස √D(X) අගය ද භාවිතා වේ.
අර්ථ දැක්වීම: සම්මත අපගමනය σ(X) සසම්භාවී විචල්‍ය X විචල්‍යයේ වර්ග මූලය ලෙස හැඳින්වේ:
කාර්ය අංක 2.විවික්ත අහඹු විචල්‍ය X බෙදාහැරීමේ නීතිය මගින් ලබා දී ඇත:
P2, බෙදා හැරීමේ ශ්‍රිතය F(x) සොයාගෙන එහි ප්‍රස්ථාරය මෙන්ම M(X), D(X), σ(X) සටහනක් සටහන් කරන්න.
විසඳුමක්: සසම්භාවී විචල්‍ය X හි විය හැකි අගයන්හි සම්භාවිතා එකතුව 1 ට සමාන වන බැවින්,
Р2=1- (0.1+0.3+0.2+0.3)=0.1
බෙදා හැරීමේ ශ්‍රිතය සොයන්න F(x)=P(X ජ්යාමිතික වශයෙන්, මෙම සමානාත්මතාවය පහත පරිදි අර්ථ දැක්විය හැක: F(x) යනු සසම්භාවී විචල්‍යයක් සැබෑ අක්ෂයේ නිරූපිත අගය x හි වමට ඇති ලක්ෂ්‍යයකින් ලබා ගැනීමේ සම්භාවිතාවයි. x≤-1 නම්, F(x)=0, මෙම අහඹු විචල්‍යයේ තනි අගයක් (-∞;x) මත නොමැති බැවින්; නම් -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; 0 නම්<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;х) අගයන් දෙකක් x1=-1 සහ x2=0 වැටීම; 1 නම්<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; 2 නම්<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; x>3 නම්, F(x)=P(X=-1) + P(X=0)+ P(X=1)+ P(X=2)+P(X=3)= 0.1 +0.1 +0.3+0.2+0.3=1, x1=-1, x2=0,x3=1,x4=2 අගයන් හතරක් (-∞;x) සහ x5=3 ට වැටෙන බැවින්. x≤-1 සඳහා https://pandia.ru/text/78/455/images/image006_89.gif" width="14 height=2" height="2"> 0, 0.1 සිට -1 දක්වා<х≤0, 0.2 ට 0<х≤1, F(x)= 0.5 ට 1<х≤2, 0.7 ට 2<х≤3, x>3 සඳහා 1 අපි F(x) ශ්‍රිතය චිත්‍රක ලෙස නිරූපණය කරමු (රූපය 3): https://pandia.ru/text/78/455/images/image014_24.jpg" width="158 height=29" height="29">≈1.2845. §
4. ද්විපද බෙදාහැරීමේ නීතිය විවික්ත අහඹු විචල්යය, පොයිසන්ගේ නියමය. අර්ථ දැක්වීම: ද්විපද
විවික්ත සසම්භාවී විචල්‍යයක් බෙදා හැරීමේ නීතිය ලෙස හැඳින්වේ X - n ස්වාධීන පුනරාවර්තන අත්හදා බැලීම් වලදී A සිදුවීමේ සිදුවීම් සංඛ්යාව, ඒ සෑම අවස්ථාවකදීම A සම්භාවිතාව p සමඟ සිදු විය හැකි හෝ සම්භාවිතාව q = 1-p සමඟ සිදු නොවේ. එවිට Р(Х=m) - n අත්හදා බැලීම්වල A හරියටම m වාරයක් සිදුවීමේ සම්භාවිතාව Bernoulli සූත්රය මගින් ගණනය කෙරේ: P(X=m)=Сmnpmqn-m ගණිතමය අපේක්ෂාව, විචලනය සහ මධ්යන්යය සම්මත අපගමනයද්විමය නියමයකට අනුව බෙදා හරින ලද අහඹු විචල්‍ය X පිළිවෙලින් සූත්‍ර මගින් සොයා ගනී: https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> A සිදුවීමේ සම්භාවිතාව - සෑම පරීක්ෂණයකදීම "පහක් ලබා ගැනීම" සමාන වන අතර 1/6 ට සමාන වේ, එනම් P(A)=p=1/6, පසුව P(A)=1-p=q=5/6, එහිදී - "බිංදු පහක් නොවේ." සසම්භාවී විචල්‍ය X අගයන් ගත හැක: 0;1;2;3. Bernoulli සූත්රය භාවිතා කරමින් X හි ඇති හැකි සෑම අගයකම සම්භාවිතාව අපි සොයා ගනිමු: P(X=0)=P3(0)=C03p0q3=1 (1/6)0 (5/6)3=125/216; P(X=1)=P3(1)=C13p1q2=3 (1/6)1 (5/6)2=75/216; P(X=2)=P3(2)=C23p2q=3(1/6)2(5/6)1=15/216; P(X=3)=P3(3)=C33p3q0=1 (1/6)3 (5/6)0=1/216. බව. සසම්භාවී විචල්‍ය X හි ව්‍යාප්ති නියමයේ ආකෘතිය ඇත: පාලනය: 125/216+75/216+15/216+1/216=1. අහඹු විචල්‍ය X හි සංඛ්යාත්මක ලක්ෂණ සොයා ගනිමු: M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, කාර්ය අංක 4.ස්වයංක්‍රීය යන්ත්‍ර මුද්දර කොටස්. නිෂ්පාදිත කොටසක් දෝෂ සහිත වීමේ සම්භාවිතාව 0.002 කි. තෝරාගත් කොටස් 1000 අතර ඇති සම්භාවිතාව සොයන්න: a) 5 දෝෂ සහිත; b) අවම වශයෙන් එකක් දෝෂ සහිතය. විසඳුමක්:
අංකය n=1000 විශාල වේ, දෝෂ සහිත කොටසක් නිෂ්පාදනය කිරීමේ සම්භාවිතාව p=0.002 කුඩා වන අතර, සලකා බලනු ලබන සිදුවීම් (කොටස දෝෂ සහිත බව පෙනේ) ස්වාධීන වේ, එබැවින් Poisson සූත්රය සිදු වේ: Рn(m)= ඊ-
λ
එම් අපි λ=np=1000 0.002=2 සොයා ගනිමු. අ) දෝෂ සහිත කොටස් 5ක් තිබීමේ සම්භාවිතාව සොයන්න (m=5): P1000(5)= ඊ-2
25
= 32 0,13534
= 0,0361 b) අඩුම තරමින් එක් දෝෂ සහිත කොටසක් හෝ ඇති වීමේ සම්භාවිතාව සොයන්න. සිදුවීම A - "තෝරාගත් කොටස් වලින් අවම වශයෙන් එකක් දෝෂ සහිතයි" යනු සිදුවීමේ ප්‍රතිවිරුද්ධයයි - "සියලු තෝරාගත් කොටස් දෝෂ සහිත නොවේ". එබැවින්, P (A) \u003d 1-P (). එබැවින් අපේක්ෂිත සම්භාවිතාව සමාන වේ: Р(А)=1-Р1000(0)=1- ඊ-2
20
\u003d 1-e-2 \u003d 1-0.13534≈0.865. ස්වාධීන වැඩ සඳහා කාර්යයන්.
1.1
1.2.
විසිරුණු සසම්භාවී විචල්‍ය X බෙදාහැරීමේ නීතිය මගින් ලබා දී ඇත: p4, බෙදා හැරීමේ ශ්‍රිතය F(X) සොයාගෙන එහි ප්‍රස්ථාරය මෙන්ම M(X), D(X), σ(X) සටහනක් සකසන්න. 1.3.
පෙට්ටියේ දැනෙන ඉඟි පෑන් 9 ක් ඇත, ඉන් 2 ක් තවදුරටත් ලියන්නේ නැත. අහඹු ලෙස, දැනෙන ඉඟි පෑන් 3 ක් ගන්න. සසම්භාවී විචල්යය X - ගත් ඒවා අතර ලියන හැඟෙන-තුඩු පෑන් ගණන. අහඹු විචල්‍යයක ව්යාප්තිය පිළිබඳ නියමය සම්පාදනය කරන්න. 1.4.
පුස්තකාල රාක්කයේ අහඹු ලෙස පෙළපොත් 6ක් තබා ඇති අතර ඉන් 4ක් බැඳ ඇත. පුස්තකාලයාධිපතියා අහඹු ලෙස පෙළපොත් 4ක් ගනී. සසම්භාවී විචල්‍ය X යනු ගත් ඒවා අතර බැඳුනු පෙළපොත් ගණනයි. අහඹු විචල්‍යයක ව්යාප්තිය පිළිබඳ නියමය සම්පාදනය කරන්න. 1.5.
ටිකට් පතේ කාර්යයන් දෙකක් ඇත. සම්භාවිතාව නිවැරදි තීරණයපළමු කාර්යය 0.9 ට සමාන වේ, දෙවන - 0.7. අහඹු විචල්‍ය X යනු ටිකට් පතේ නිවැරදිව විසඳා ඇති ගැටළු ගණනයි. බෙදා හැරීමේ නියමයක් සම්පාදනය කරන්න, මෙම අහඹු විචල්‍යයේ ගණිතමය අපේක්ෂාව සහ විචලනය ගණනය කරන්න, තවද F (x) බෙදා හැරීමේ ශ්‍රිතය සොයාගෙන එහි ප්‍රස්ථාරය ගොඩනඟන්න. 1.6.
වෙඩික්කරුවන් තිදෙනෙකු ඉලක්කයකට වෙඩි තබයි. පළමු වෙඩික්කරු සඳහා එක් පහරකින් ඉලක්කයට පහර දීමේ සම්භාවිතාව 0.5, දෙවන - 0.8, තෙවන - 0.7. සසම්භාවී විචල්‍ය X යනු වෙඩික්කරුවන් එක් පහරක් බැගින් එල්ල කළහොත් ඉලක්කයට එල්ල වන පහර ගණනයි. බෙදා හැරීමේ නීතිය, M(X),D(X) සොයන්න. 1.7.
පැසිපන්දු ක්‍රීඩකයෙක් පන්දුව කූඩයට විසි කරන්නේ එක් එක් විසි කිරීමකදී 0.8ක් වැදීමේ සම්භාවිතාවක් සහිතවය. සෑම පහරක් සඳහාම, ඔහුට ලකුණු 10 ක් ලැබෙන අතර, අතපසු වූ විට, ඔහුට ලකුණු ප්‍රදානය නොකෙරේ. අහඹු විචල්‍යයක් බෙදා හැරීමේ නියමය සම්පාදනය කරන්න, විසි කිරීම් 3ක් සඳහා පැසිපන්දු ක්‍රීඩකයෙකුට ලැබුණු ලකුණු සංඛ්යාව X. M(X),D(X) සහ ඔහු ලකුණු 10කට වඩා ලබා ගැනීමේ සම්භාවිතාව සොයන්න. 1.8.
කාඩ්පත් මත අකුරු ලියා ඇත, ස්වර 5 ක් සහ ව්යාංජනාක්ෂර 3 ක් පමණි. කාඩ්පත් 3 ක් අහඹු ලෙස තෝරාගෙන ඇති අතර, ලබාගත් කාඩ්පත ආපසු ලබා දෙන සෑම අවස්ථාවකම. සසම්භාවී විචල්යය X යනු ගත් ඒවා අතර ඇති ස්වර ගණනයි. බෙදා හැරීමේ නීතියක් සම්පාදනය කර M(X),D(X),σ(X) සොයා ගන්න. 1.9.
සාමාන්යයෙන්, ගිවිසුම් වලින් 60% රක්ෂණ සමාගමරක්ෂිත සිදුවීමක් සිදුවීම සම්බන්ධයෙන් රක්ෂිත මුදල් ගෙවයි. සසම්භාවී විචල්‍ය X සඳහා බෙදා හැරීමේ නීතියක් අඳින්න - අහඹු ලෙස තෝරාගත් කොන්ත්‍රාත්තු හතරක් අතරින් රක්ෂිත මුදල ගෙවා ඇති කොන්ත්‍රාත්තු ගණන. මෙම ප්‍රමාණයේ සංඛ්යාත්මක ලක්ෂණ සොයන්න. 1.10.
ගුවන්විදුලි මධ්‍යස්ථානය නිශ්චිත කාල පරාසයන් තුළ ද්වි-මාර්ග සන්නිවේදනය ස්ථාපිත කරන තෙක් ඇමතුම් සංඥා (හතරකට නොවැඩි) යවයි. ඇමතුම් ලකුණකට ප්රතිචාරයක් ලැබීමේ සම්භාවිතාව 0.3 කි. සසම්භාවී විචල්‍ය X-යවන ලද ඇමතුම් සංඥා ගණන. බෙදා හැරීමේ නීතිය සම්පාදනය කර F(x) සොයා ගන්න. 1.11.
යතුරු 3 ක් ඇත, එයින් එකක් පමණක් අගුලට ගැලපේ. උත්සාහ කළ යතුර පසුකාලීන උත්සාහයන්ට සහභාගී නොවන්නේ නම්, අහඹු විචල්‍ය X-අඟුල විවෘත කිරීමට දරන උත්සාහයන් සඳහා බෙදා හැරීමේ නීතියක් අඳින්න. M(X),D(X) සොයන්න. 1.12.
විශ්වසනීයත්වය සඳහා උපාංග තුනක අනුක්රමික ස්වාධීන පරීක්ෂණ සිදු කරනු ලැබේ. සෑම ඊළඟ සවිකිරීමපරීක්ෂා කරනු ලබන්නේ පෙර එක විශ්වාසදායක බව ඔප්පු වුවහොත් පමණි. එක් එක් උපකරණ සඳහා පරීක්ෂණය සමත් වීමේ සම්භාවිතාව 0.9 කි. පරීක්ෂා කරන ලද උපාංගවල අහඹු විචල්‍ය X-සංඛ්යාව බෙදා හැරීමේ නියමය සම්පාදනය කරන්න. 1.13
.විවික්ත අහඹු විචල්‍ය X හට හැකි අගයන් තුනක් ඇත: x1=1, x2, x3, සහ x1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
ඉලෙක්ට්රොනික උපාංගයේ බ්ලොක් එක සමාන මූලද්රව්ය 100 ක් අඩංගු වේ. T කාලය තුළ එක් එක් මූලද්රව්යයේ අසමත් වීමේ සම්භාවිතාව 0.002 ට සමාන වේ. මූලද්රව්ය ස්වාධීනව ක්රියා කරයි. T කාලය තුළ මූලද්රව්ය දෙකකට වඩා අසමත් වීමේ සම්භාවිතාව සොයන්න. 1.15.
පෙළපොත පිටපත් 50,000 කින් ප්රකාශයට පත් විය. පෙළපොත වැරදි ලෙස බැඳී ඇති සම්භාවිතාව 0.0002 වේ. සංසරණය අඩංගු සම්භාවිතාව සොයන්න: අ) දෝෂ සහිත පොත් හතරක්, ආ) දෝෂ සහිත පොත් දෙකකට වඩා අඩුය. 1
.16.
සෑම මිනිත්තුවකම PBX වෙත පැමිණෙන ඇමතුම් ගණන λ=1.5 පරාමිතිය සමඟ Poisson නීතියට අනුව බෙදා හරිනු ලැබේ. මිනිත්තුවකින් ඇති විය හැකි සම්භාවිතාව සොයන්න: අ) ඇමතුම් දෙකක්; ආ) අවම වශයෙන් එක් ඇමතුමක්. 1.17.
Z=3X+Y නම් M(Z),D(Z) සොයන්න. 1.18.
ස්වාධීන අහඹු විචල්‍ය දෙකක බෙදා හැරීමේ නීති ලබා දී ඇත: Z=X+2Y නම් M(Z),D(Z) සොයන්න. පිළිතුරු:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110"> 1.1.
p3=0.4; x≤-2 සඳහා 0, 0.3 සිට -2 දක්වා<х≤0, F(x)= 0.5 ට 0<х≤2, 0.9 ට 2<х≤5, x>5 සඳහා 1 0.3 සිට -1 දක්වා<х≤0, 0.4 ට 0<х≤1, F(x)= 0.6 at 1<х≤2, 0.7 ට 2<х≤3, x>3 සඳහා 1 M(X)=1; D(X)=2.6; σ(X) ≈1.612. x≤0 සඳහා https://pandia.ru/text/78/455/images/image025_24.gif" width="2 height=98" height="98"> 0, 0.03 ට 0<х≤1, F(x)= 0.37 ට 1<х≤2, x>2 සඳහා 1 M(X)=2; D(X)=0.62 M(X)=2.4; D(X)=0.48, P(X>10)=0.896 1.
8
.
M(X)=15/8; D(X)=45/64; σ(Х) ≈ M(X)=2.4; D(X)=0.96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(X)=2; D(X)=2/3 1.14.
1.22e-0.2≈0.999 1.15.
a) 0.0189; ආ) 0.00049 1.16.
a) 0.0702; ආ) 0.77687 1.17.
3,8; 14,2 1.18.
11,2; 4. 2 වන පරිච්ඡේදය අඛණ්ඩ අහඹු විචල්යය
අර්ථ දැක්වීම: අඛණ්ඩ
අගය නම් කරන්න, හැකි සියලුම අගයන් සංඛ්යාත්මක අක්ෂයේ පරිමිත හෝ අසීමිත පරතරය සම්පූර්ණයෙන්ම පුරවන්න. පැහැදිලිවම, අඛණ්ඩ අහඹු විචල්‍යයක විය හැකි අගයන් ගණන අනන්තය. අඛණ්ඩ අහඹු විචල්‍යයක් බෙදා හැරීමේ ශ්‍රිතයක් භාවිතයෙන් නියම කළ හැක. අර්ථ දැක්වීම:එෆ් බෙදා හැරීමේ කාර්යය
අඛණ්ඩ අහඹු විචල්‍ය X යනු F(x) ශ්‍රිතයක් වන අතර එය එක් එක් අගය සඳහා xhttps://pandia.ru/text/78/455/images/image028_11.jpg" width="14" height="13">R තීරණය කරයි. බෙදා හැරීමේ ශ්‍රිතය සමහර විට සමුච්චිත ව්‍යාප්ති ශ්‍රිතය ලෙස හැඳින්වේ. බෙදා හැරීමේ ක්‍රියාකාරී ගුණාංග:
1)1≤F(x)≤1 2) අඛණ්ඩ අහඹු විචල්‍යයක් සඳහා, බෙදා හැරීමේ ශ්‍රිතය ඕනෑම ලක්ෂ්‍යයක අඛණ්ඩ වන අතර සමහර විට තනි ලක්ෂ්යවලදී හැර සෑම තැනකම අවකලනය කළ හැකිය. 3) සසම්භාවී විචල්‍යයක් X අන්තරයන් (a; b), [a; b), [a; b] එකකට වැටෙන සම්භාවිතාව F (x) ශ්‍රිතයේ අගයන් අතර වෙනසට සමාන වේ. a සහ b ලක්ෂ්යවලදී, i.e. පී(ඒ<Х 4) අඛණ්ඩ සසම්භාවී විචල්‍ය X එක තනි අගයක් ගැනීමේ සම්භාවිතාව 0 වේ. 5) F(-∞)=0, F(+∞)=1 බෙදා හැරීමේ ශ්‍රිතයක් භාවිතයෙන් අඛණ්ඩ අහඹු විචල්‍යයක් නියම කිරීම එකම එක නොවේ. සම්භාවිතා ව්‍යාප්ති ඝනත්වය (බෙදාහැරීමේ ඝනත්වය) සංකල්පය හඳුන්වා දෙමු. අර්ථ දැක්වීම
:
සම්භාවිතා ඝනත්වය
f
(
x
)
අඛණ්ඩ සසම්භාවී විචල්‍ය X යනු එහි ව්‍යාප්ති ශ්‍රිතයේ ව්‍යුත්පන්නයයි, එනම්: සම්භාවිතා ව්‍යාප්ති ඝනත්වය සමහර විට අවකල ව්‍යාප්ති ශ්‍රිතය හෝ අවකල ව්‍යාප්ති නියමය ලෙස හැඳින්වේ. සම්භාවිතා ව්‍යාප්තියේ ඝනත්වයේ ප්‍රස්ථාරය f(x) ලෙස හැඳින්වේ සම්භාවිතා බෙදා හැරීමේ වක්රය
.
සම්භාවිතා ඝනත්ව ගුණාංග:
1) f(x) ≥0, විට xhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" height="141">.gif" width="14" උස x≤2 සඳහා ="62 src="> 0, f(x)= c(x-2) at 2<х≤6, x>6 සඳහා 0. සොයන්න: a) c හි අගය; ආ) බෙදා හැරීමේ ශ්‍රිතය F(x) සහ එහි ප්‍රස්ථාරය ගොඩනඟන්න; ඇ) Р(3≤х<5) විසඳුමක්:
+
∞ a) සාමාන්‍යකරණ තත්ත්වයෙන් c හි අගය සොයන්න: ∫ f(x)dx=1. එබැවින්, -∞ https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> -∞ 2 2 x 2 නම්<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х - (4/2-4))= 1/8(x2/2-2x+2)=1/16(x-2)2; x≤2 සඳහා Gif" width="14" height="62"> 0, F (x) \u003d (x-2) 2/16 ට 2<х≤6, x>6 සඳහා 1. F(x) ශ්‍රිතයේ ප්‍රස්ථාරය රූප සටහන 3 හි දැක්වේ x≤0 සඳහා https://pandia.ru/text/78/455/images/image034_23.gif" width="14" height="62 src="> 0, F (x) \u003d (3 arctg x) / π 0 ට<х≤√3, x>√3 සඳහා 1. අවකල ව්‍යාප්ති ශ්‍රිතය f(x) සොයන්න විසඳුමක්:
f (x) \u003d F '(x) සිට, පසුව https://pandia.ru/text/78/455/images/image011_36.jpg" width="118" height="24"> විසුරුවා හරින ලද අහඹු විචල්යයන් සඳහා කලින් සලකා බැලූ ගණිතමය අපේක්ෂාවේ සහ විසරණයේ සියලුම ගුණාංග අඛණ්ඩ ඒවා සඳහා ද වලංගු වේ. කාර්ය අංක 3.සසම්භාවී විචල්‍ය X ලබා දී ඇත අවකල කාර්යය f(x): https://pandia.ru/text/78/455/images/image036_19.gif" height="38"> -∞ 2 X3/9 + x2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> +∞ D(X)= ∫ x2 f(x)dx-(M(x))2=∫ x2 x/3 dx+∫1/3x2 dx=(31/18)2=x4/12 +x3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> පී(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. ස්වාධීන විසඳුමක් සඳහා කාර්යයන්.
2.1.
අඛණ්ඩ සසම්භාවී විචල්‍ය X බෙදා හැරීමේ ශ්‍රිතයක් මඟින් ලබා දේ: x≤0 සඳහා 0, x≤ π/6 සඳහා F(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0, F(х)= - π/6 ට 3x<х≤ π/3, x> π/3 සඳහා 1. අවකල ව්‍යාප්ති ශ්‍රිතය f(x) සහ ද සොයන්න ආර්(2π /9<Х< π /2). 2.3.
x≤2 සඳහා 0, f(x)= x සමඟ 2<х≤4, x>4 සඳහා 0. 2.4.
අඛණ්ඩ සසම්භාවී විචල්‍ය X බෙදාහැරීමේ ඝනත්වය මගින් දෙනු ලැබේ: x≤0 සඳහා 0, f(х)= с √х 0 ට<х≤1, x>1 සඳහා 0. සොයන්න: a) අංකය c; b) M(X), D(X). 2.5.
x සඳහා https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" height="39">, x ට 0. සොයන්න: අ) F(x) සහ එහි ප්‍රස්ථාරය සටහන් කරන්න; b) M(X),D(X), σ(X); ඇ) හතරකින් ඇති සම්භාවිතාව ස්වාධීන පරීක්ෂණ X අගය පරතරයට අයත් අගය මෙන් හරියටම 2 ගුණයක් ගනී (1; 4). 2.6.
අඛණ්ඩ සසම්භාවී විචල්‍ය X හි සම්භාවිතා ව්‍යාප්ති ඝනත්වය ලබා දී ඇත: x සඳහා f (x) \u003d 2 (x-2), x ට 0. සොයන්න: අ) F(x) සහ එහි ප්‍රස්ථාරය සටහන් කරන්න; b) M(X),D(X), σ(X); ඇ) ස්වාධීන පරීක්ෂණ තුනකදී X අගය පරතරයට අයත් අගය මෙන් 2 ගුණයක් ගන්නා සම්භාවිතාව . 2.7.
f(x) ශ්‍රිතය ලබා දී ඇත්තේ: https://pandia.ru/text/78/455/images/image045_4.jpg" width="43" height="38 src=">.jpg" width="16" height="15">[-√ 3/2; √3/2]. 2.8.
f(x) ශ්‍රිතය ලබා දී ඇත්තේ: https://pandia.ru/text/78/455/images/image046_5.jpg" width="45" height="36 src="> .jpg" width="16" height="15">[- π /හතර ; π /4]. සොයන්න: a) යම් අහඹු විචල්‍ය X හි ශ්‍රිතය සම්භාවිතා ඝනත්වය වන නියත c හි අගය; b) බෙදා හැරීමේ කාර්යය F(x). 2.9.
සසම්භාවී විචල්‍ය Х, අන්තරය (3;7) මත සංකේන්ද්‍රණය වී F(х)= බෙදා හැරීමේ ශ්‍රිතය මඟින් ලබා දේ. ඒ සම්භාවිතාව සොයන්න සසම්භාවී විචල්‍ය X අගය ගනී: a) 5 ට අඩු, b) 7 ට නොඅඩු. 2.10.
සසම්භාවී විචල්යය X, අන්තරය මත සංකේන්ද්‍රණය වී ඇත (-1; 4), F(x)= බෙදා හැරීමේ ශ්‍රිතය මගින් ලබා දී ඇත. ඒ සම්භාවිතාව සොයන්න සසම්භාවී විචල්‍ය X අගය ගනී: a) 2 ට අඩු, b) 4 ට නොඅඩු. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" height="44 src="> .jpg" width="16" height="15">. සොයන්න: a) අංකය c; b) M(X); ඇ) සම්භාවිතාව P(X > M(X)). 2.12.
අහඹු විචල්යය ලබා දෙන්නේ අවකල ව්‍යාප්ති ශ්‍රිතය මගිනි: https://pandia.ru/text/78/455/images/image050_3.jpg" width="60" height="38 src=">.jpg" width="16 height=15" height="15"> . සොයන්න: a) M(X); ආ) සම්භාවිතාව Р(Х≤М(Х)) 2.13.
කාල ව්යාප්තිය සම්භාවිතා ඝනත්වය මගින් දෙනු ලැබේ: x ≥0 සඳහා https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" height="37">. f(x) යනු සම්භාවිතා ඝනත්ව ව්‍යාප්තියක් බව ඔප්පු කරන්න. 2.14.
අඛණ්ඩ සසම්භාවී විචල්‍ය X හි සම්භාවිතා ව්‍යාප්ති ඝනත්වය ලබා දී ඇත: https://pandia.ru/text/78/455/images/image054_3.jpg" width="174" height="136 src="> (fig.4) 2.16.
අහඹු විචල්‍ය X ව්‍යවස්ථාව අනුව බෙදා හරිනු ලැබේ " සෘජු ත්රිකෝණය»විරාමයේ (0;4) (Fig.5). සම්භාවිතා ඝනත්වය f(x) සඳහා සම්පූර්ණ සැබෑ අක්ෂයේ විශ්ලේෂණාත්මක ප්‍රකාශනයක් සොයන්න. පිළිතුරු
x≤0 සඳහා 0, f(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> x≤ π/6 සඳහා, F(x)= 3sin 3x π/6 ට<х≤ π/3, x> π/3 සඳහා 0. අඛණ්ඩ සසම්භාවී විචල්‍යයක් X සතුව ඇත ඒකාකාර නීතියයම් කාල පරතරයක් මත බෙදා හැරීම (a; b), X හි සියලු හැකි අගයන් අයත් වේ, සම්භාවිතා ව්‍යාප්ති ඝනත්වය f (x) මෙම පරතරය මත නියත වන අතර ඉන් පිටත 0 ට සමාන වේ නම්, i.e. x≤a සඳහා 0, f(x)= a සඳහා<х x≥b සඳහා 0. f(x) ශ්‍රිතයේ ප්‍රස්ථාරය රූපයේ දැක්වේ. එක F(х)= https://pandia.ru/text/78/455/images/image077_3.jpg" width="30" height="37">, D(X)=, σ(Х)=. කාර්ය අංක 1.සසම්භාවී විචල්යය X කොටසෙහි ඒකාකාරව බෙදා හැරේ. සොයන්න: අ) සම්භාවිතා ව්යාප්තිය ඝනත්වය f(x) සහ එහි ප්‍රස්ථාරය ගොඩනැගීම; ආ) බෙදා හැරීමේ ශ්‍රිතය F(x) සහ එහි ප්‍රස්ථාරය ගොඩනඟන්න; ඇ) M(X),D(X), σ(X). විසඳුමක්:
a=3, b=7 සමඟ ඉහත සාකච්ඡා කර ඇති සූත්‍ර භාවිතා කරමින්, අපි සොයා ගන්නේ: https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" height="39"> 3≤х≤7, x>7 සඳහා 0 අපි එහි ප්‍රස්ථාරය ගොඩනඟමු (රූපය 3): x≤3 සඳහා https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86 src="> 0, F(х)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" height="119 src=">fig.4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" height="43">==https://pandia.ru/text/ x සඳහා 78/455/images/image092_10.gif" width="14" height="49 src="> 0<0, f(х)= λе-λх දී x≥0. ඝාතීය නියමයකට අනුව බෙදා හරින ලද අහඹු විචල්‍ය X හි ව්‍යාප්ති ශ්‍රිතය සූත්රය මගින් දෙනු ලැබේ: https://pandia.ru/text/78/455/images/image094_4.jpg" width="191" height="126 src=">fig..jpg" width="22" height="30"> , D(X)=, σ(X)= මේ අනුව, ඝාතීය ව්‍යාප්තියේ ගණිතමය අපේක්ෂාව සහ සම්මත අපගමනය එකිනෙකට සමාන වේ. X හි පරතරය (a;b) ට වැටීමේ සම්භාවිතාව සූත්රය මගින් ගණනය කෙරේ: ආර්(ඒ<Х කාර්ය අංක 2.උපාංගයේ සාමාන්ය ක්‍රියාකාරී කාලය පැය 100 කි. උපාංගයේ අතිකාලයට ඝාතීය බෙදා හැරීමේ නීතියක් ඇතැයි උපකල්පනය කරමින්, සොයන්න: a) සම්භාවිතා බෙදා හැරීමේ ඝනත්වය; b) බෙදා හැරීමේ කාර්යය; ඇ) උපාංගයේ අසාර්ථක-නිදහස් මෙහෙයුම් කාලය පැය 120 ඉක්මවන සම්භාවිතාව. විසඳුමක්:
කොන්දේසිය අනුව, ගණිතමය ව්යාප්තිය M(X)=https://pandia.ru/text/78/455/images/image098_10.gif" height="43 src="> x සඳහා 0<0, a) f(x)= x≥0 සඳහා 0.01e -0.01x. b) x සඳහා F(x)= 0<0, x≥0 හි 1-e -0.01x. ඇ) බෙදා හැරීමේ ශ්‍රිතය භාවිතයෙන් අපි අපේක්ෂිත සම්භාවිතාව සොයා ගනිමු: P(X>120)=1-F(120)=1-(1-e-1.2)=e-1.2≈0.3. §
3.සාමාන්ය බෙදාහැරීමේ නීතිය අර්ථ දැක්වීම:
අඛණ්ඩ සසම්භාවී විචල්‍යයක් X සතුව ඇත සාමාන්ය බෙදාහැරීමේ නීතිය (ගවුසියානු නීතිය),
එහි ව්යාප්තිය ඝනත්වයට ආකෘතිය තිබේ නම්: මෙහි m=M(X), σ2=D(X), σ>0. සාමාන්ය බෙදාහැරීමේ වක්රය ලෙස හැඳින්වේ සාමාන්ය හෝ gaussian වක්රය
(Fig.7) සාමාන්ය නීතියට අනුව බෙදා හරින ලද අහඹු විචල්‍ය X හි බෙදා හැරීමේ ශ්‍රිතය සූත්‍රයට අනුව Laplace ශ්‍රිතය Ф (х) හරහා ප්‍රකාශ වේ: Laplace ශ්‍රිතය කොහෙද. අදහස් දැක්වීම:
Ф(х) ශ්‍රිතය ඔත්තේ (Ф(-х)=-Ф(х)), අමතරව, x>5 නම්, අපට Ф(х) ≈1/2 සලකා බැලිය හැක. F(x) ව්‍යාප්ති ශ්‍රිතයේ ප්‍රස්ථාරය රූපයේ දැක්වේ. අට https://pandia.ru/text/78/455/images/image106_4.jpg" width="218" height="33"> සම්භාවිතාව නිරපේක්ෂ වටිනාකමඅපගමනය අඩු වේ ධනාත්මක අංකයδ සූත්රය මගින් ගණනය කරනු ලැබේ: විශේෂයෙන්ම, m=0 සඳහා සමානාත්මතාවය සත්‍ය වේ: "තුන සිග්මා රීතිය"
සසම්භාවී විචල්‍ය X හි m සහ σ යන පරාමිති සහිත සාමාන්ය ව්‍යාප්ති නියමයක් තිබේ නම්, ප්‍රායෝගිකව එහි අගය පවතිනුයේ අන්තරය (a-3σ; a+3σ), නිසා https://pandia.ru/text/78/455/images/image110_2.jpg" width="157" height="57 src=">a) ආ) අපි සූත්රය භාවිතා කරමු: https://pandia.ru/text/78/455/images/image112_2.jpg" width="369" height="38 src="> Ф(х) ශ්‍රිතයේ අගයන් වගුවට අනුව අපට Ф(1.5)=0.4332, Ф(1)=0.3413 හමු වේ. එබැවින් අපේක්ෂිත සම්භාවිතාව වන්නේ: පී(28 ස්වාධීන වැඩ සඳහා කාර්යයන්
3.1.
සසම්භාවී විචල්යය X අන්තරය තුළ ඒකාකාරව බෙදා හැරේ (-3;5). සොයන්න: b) බෙදා හැරීමේ කාර්යය F(x); ඇ) සංඛ්යාත්මක ලක්ෂණ; ඈ) සම්භාවිතාව P(4<х<6). 3.2.
සසම්භාවී විචල්යය X කොටසෙහි ඒකාකාරව බෙදා හැරේ. සොයන්න: a) බෙදාහැරීමේ ඝනත්වය f(x); b) බෙදා හැරීමේ කාර්යය F(x); ඇ) සංඛ්යාත්මක ලක්ෂණ; ඈ) සම්භාවිතාව Р(3≤х≤6). 3.3.
අධිවේගී මාර්ගයේ ස්වයංක්‍රීය රථවාහන ආලෝකයක් සවි කර ඇති අතර, වාහන සඳහා හරිත ආලෝකය මිනිත්තු 2 ක් ද, තත්පර 3 ක් කහ සහ තත්පර 30 ක් රතු යනාදිය ද දැල්වෙයි. මෝටර් රථය අහඹු ලෙස අධිවේගී මාර්ගය ඔස්සේ ගමන් කරයි. මෝටර් රථය නතර නොවී රථවාහන ආලෝකය පසුකර යාමේ සම්භාවිතාව සොයන්න. 3.4.
උමං දුම්රිය විනාඩි 2 ක පරතරයකින් නිතිපතා ධාවනය වේ. මගියා අහඹු ලෙස වේදිකාවට ඇතුළු වේ. මගියාට දුම්රිය සඳහා තත්පර 50 කට වඩා රැඳී සිටීමට සිදු වන සම්භාවිතාව කුමක්ද? අහඹු විචල්‍ය X හි ගණිතමය අපේක්ෂාව සොයන්න - දුම්රියේ රැඳී සිටින කාලය. 3.5.
බෙදා හැරීමේ ශ්‍රිතය මඟින් ලබා දෙන ඝාතීය ව්‍යාප්තියේ විචලනය සහ සම්මත අපගමනය සොයන්න: F(x)= x හි 0<0, x≥0 සඳහා 1-e-8x. 3.6.
අඛණ්ඩ සසම්භාවී විචල්‍යයක් X සම්භාවිතා ව්‍යාප්ති ඝනත්වය මගින් දෙනු ලැබේ: f(x)=0 x ට<0, x≥0 හි 0.7 e-0.7x. අ) සලකා බලන අහඹු විචල්‍යයේ ව්‍යාප්ති නීතිය නම් කරන්න. b) බෙදා හැරීමේ ශ්‍රිතය F(X) සහ සසම්භාවී විචල්‍ය X හි සංඛ්යාත්මක ලක්ෂණ සොයන්න. 3.7.
සසම්භාවී විචල්‍ය X සම්භාවිතා ව්‍යාප්ති ඝනත්වය මගින් ලබා දී ඇති ඝාතීය නියමය අනුව බෙදා හරිනු ලැබේ: f(x)=0 x ට<0, x≥0 හි 0.4 e-0.4 x. පරීක්ෂණයේ ප්රතිඵලයක් ලෙස, X පරතරයෙන් (2.5; 5) අගයක් ගන්නා සම්භාවිතාව සොයන්න. 3.8.
අඛණ්ඩ සසම්භාවී විචල්‍ය X බෙදා හැරීමේ ශ්‍රිතය මගින් ලබා දී ඇති ඝාතීය නියමය අනුව බෙදා හරිනු ලැබේ: F(x)= x හි 0<0, x≥0 හි 1 වන-0.6x පරීක්ෂණයේ ප්රතිඵලයක් ලෙස, X පරතරයෙන් අගයක් ගන්නා සම්භාවිතාව සොයන්න. 3.9.
සාමාන්යයෙන් බෙදා හරින අහඹු විචල්‍යයක ගණිතමය අපේක්ෂාව සහ සම්මත අපගමනය පිළිවෙලින් 8 සහ 2 වේ. සොයන්න: a) බෙදාහැරීමේ ඝනත්වය f(x); b) පරීක්ෂණයේ ප්රතිඵලයක් ලෙස X, පරතරයෙන් අගයක් ගන්නා සම්භාවිතාව (10;14). 3.10.
සසම්භාවී විචල්‍ය X සාමාන්යයෙන් මධ්‍යන්‍ය 3.5 සහ විචල්‍ය 0.04 සමඟ බෙදා හරිනු ලැබේ. සොයන්න: a) බෙදාහැරීමේ ඝනත්වය f(x); b) පරීක්ෂණයේ ප්රතිඵලයක් ලෙස X පරතරයෙන් අගයක් ගන්නා සම්භාවිතාව . 3.11.
සසම්භාවී විචල්‍ය X සාමාන්යයෙන් M(X)=0 සහ D(X)=1 සමඟ බෙදා හැරේ. කුමන සිදුවීම්: |X|≤0.6 හෝ |X|≥0.6 වැඩි සම්භාවිතාවක් තිබේද? 3.12.
සසම්භාවී විචල්‍ය X සාමාන්යයෙන් M(X)=0 සහ D(X)=1 සමඟ බෙදා හරිනු ලැබේ. එක් පරීක්ෂණයකදී (-0.5;-0.1) හෝ (1;2) එය වැඩි අගයක් ගනී. සම්භාවිතාව? 3.13.
M(X)=10den සමඟ සාමාන්ය බෙදාහැරීමක් භාවිතයෙන් කොටසක වත්මන් මිල ආදර්ශණය කළ හැක. ඒකක සහ σ (X)=0.3 ගුනය. ඒකක සොයන්න: අ) වත්මන් කොටස් මිල den 9.8 සිට වීමට ඇති සම්භාවිතාව. ඒකක 10.4 දක්වා. ඒකක; ආ) "සිග්මා තුනේ රීතිය" භාවිතා කරමින් තොගයේ වත්මන් මිල පිහිටා ඇති මායිම් සොයා ගැනීම. 3.14.
ද්රව්යය ක්රමානුකූල දෝෂයකින් තොරව කිරා මැන බලයි. අහඹු බර කිරන දෝෂ මූල-මධ්‍යන්-චතුරස්‍ර අනුපාතය σ=5r සමඟ සාමාන්ය නීතියට යටත් වේ. ස්වාධීන අත්හදා බැලීම් හතරකදී බර කිරුම් තුනක දෝෂය නිරපේක්ෂ අගය 3r හි සිදු නොවන සම්භාවිතාව සොයන්න. 3.15.
සසම්භාවී විචල්‍ය X සාමාන්යයෙන් M(X)=12.6 සමඟ බෙදා හරිනු ලැබේ. අහඹු විචල්‍යයක පරතරය (11.4;13.8) තුළට වැටීමේ සම්භාවිතාව 0.6826 වේ. සම්මත අපගමනය σ සොයන්න. 3.16.
සසම්භාවී විචල්‍ය X සාමාන්යයෙන් බෙදා හරිනු ලබන්නේ M(X)=12 සහ D(X)=36 සමඟිනි. පරීක්ෂණයේ ප්රතිඵලයක් ලෙස 0.9973 සම්භාවිතාවක් සහිතව, සසම්භාවී විචල්‍ය X පහත වැටෙන විරාමය සොයන්න. 3.17.
ස්වයංක්‍රීය යන්ත්‍රයකින් නිෂ්පාදනය කරන ලද කොටසක් එහි පාලිත පරාමිතියේ නාමික අගයෙන් X අපගමනය මොඩියුලයේ මිනුම් ඒකක 2 ඉක්මවන්නේ නම් දෝෂ සහිත යැයි සැලකේ. සසම්භාවී විචල්‍ය X සාමාන්යයෙන් M(X)=0 සහ σ(X)=0.7 සමඟ බෙදා හරිනු ලැබේ යැයි උපකල්පනය කෙරේ. යන්ත්‍රය දෝෂ සහිත කොටස් වලින් කොපමණ ප්‍රතිශතයක් ලබා දෙයිද? 3.18.
විස්තර පරාමිතිය X සාමාන්යයෙන් බෙදා හරිනු ලබන්නේ නාමික අගයට සමාන 2 ක ගණිතමය අපේක්ෂාවක් සහ 0.014 හි සම්මත අපගමනයෙනි. මුහුණත අගය මොඩියුලයෙන් X හි අපගමනය මුහුණත අගයෙන් 1% නොඉක්මවන සම්භාවිතාව සොයන්න. පිළිතුරු
https://pandia.ru/text/78/455/images/image116_9.gif" width="14" height="110 src="> b) x≤-3 සඳහා 0, F(x)=left"> 3.10.
a)f(x)= , b) Р(3.1≤Х≤3.7) ≈0.8185. 3.11.
|x|≥0.6. 3.12.
(-0,5;-0,1). 3.13.
a) Р(9.8≤Х≤10.4) ≈0.6562. 3.14.
0,111. 3.15.
σ=1.2. 3.16.
(-6;30). 3.17.
0,4%. අහඹු විචල්‍ය X හි බෙදා හැරීමේ නියමය: උදාහරණ #2. පළමු වෙඩික්කරු සඳහා එක් වෙඩි තැබීමකින් එක් වෙඩික්කරුවෙකු විසින් ඉලක්කයට පහර දීමේ සම්භාවිතාව 0.8, දෙවන වෙඩික්කරු සඳහා - 0.85. වෙඩික්කරුවන් ඉලක්කයට එක් වෙඩි පහරක් එල්ල කළේය. තනි වෙඩික්කරුවන් සඳහා ඉලක්කයට පහර දීම ස්වාධීන සිදුවීම් ලෙස උපකල්පනය කරමින්, A සිදුවීමේ සම්භාවිතාව සොයා ගන්න - ඉලක්කයට හරියටම එක් පහරක්. සසම්භාවී විචල්යය
විවිධ තත්වයන් මත පදනම්ව නිශ්චිත අගයන් ගත හැකි විචල්‍යයක් ලෙස හැඳින්වේ, සහ අනෙක් අතට, අහඹු විචල්‍යයක් ලෙස හැඳින්වේ විවික්ත
එහි අගයන් සමූහය සීමිත හෝ ගණන් කළ හැකි නම්. විවික්ත සසම්භාවී විචල්‍යයන්ට අමතරව අඛණ්ඩ අහඹු විචල්යයන් ද ඇත. සසම්භාවී විචල්‍යයක සංකල්පය අපි වඩාත් විස්තරාත්මකව සලකා බලමු. ප්‍රායෝගිකව, බොහෝ විට ඇතැම් අගයන් ගත හැකි ප්‍රමාණ ඇත, නමුත් සලකා බලනු ලබන අත්හදා බැලීම, සංසිද්ධිය, නිරීක්ෂණ වලදී ඒ සෑම එකක්ම කුමන අගයක් ගනීද යන්න විශ්වාසදායක ලෙස පුරෝකථනය කළ නොහැක. නිදසුනක් වශයෙන්, ඊළඟ දවසේ මොස්කව්හි උපත ලබන පිරිමි ළමයින් සංඛ්යාව වෙනස් විය හැකිය. එය බිංදුවට සමාන විය හැකිය (එක පිරිමි ළමයෙක්වත් ඉපදෙන්නේ නැත: සියලුම ගැහැණු ළමයින් ඉපදෙනු ඇත හෝ අලුත උපන් දරුවන් නොසිටිනු ඇත), එකක්, දෙකක්, සහ තවත් සීමිත සංඛ්යාවක් දක්වා n. එවැනි අගයන් ඇතුළත් වේ: වෙබ් අඩවියේ සීනි බීට් මුල්වල ස්කන්ධය, කාලතුවක්කු කවචයක පියාසර පරාසය, කණ්ඩායමක දෝෂ සහිත කොටස් ගණන සහ යනාදිය. එවැනි අගයන් අහඹු ලෙස හැඳින්වේ. ඔවුන් ප්‍රමාණාත්මක දෘෂ්ටි කෝණයකින් අත්හදා බැලීමක හෝ නිරීක්ෂණයක ඇති විය හැකි සියලුම ප්රතිඵල සංලක්ෂිත කරයි. විවික්ත අහඹු විචල්‍ය සඳහා උදාහරණ
සීමිත අගයන් සමඟ, ජනාවාසයක දිවා කාලයේ උපත ලබන දරුවන්ගේ සංඛ්යාව, බස් මගීන් සංඛ්යාව, මොස්කව් මෙට්රෝ විසින් දිනකට ප්රවාහනය කරන මගීන් සංඛ්යාව ආදිය සේවය කළ හැකිය. විවික්ත අහඹු විචල්‍යයක අගයන් ගණන අනන්ත විය හැකි නමුත් එය ගණන් කළ හැකි කට්ටලයකි. නමුත් ඕනෑම අවස්ථාවක, ඒවා යම් අනුපිළිවෙලකට අංකනය කළ හැකිය, නැතහොත්, වඩාත් නිවැරදිව, අහඹු විචල්‍යයක අගයන් සහ ස්වාභාවික සංඛ්යා 1, 2, 3, ..., අතර එකින් එක ලිපි හුවමාරුවක් ස්ථාපිත කළ හැකිය. n. අවධානය: සම්භාවිතා න්‍යායේ නව, ඉතා වැදගත් සංකල්පයක් - බෙදාහැරීමේ නීතිය
. ඉඩ xගත හැක nඅගයන්:. ඒවා සියල්ලම වෙනස් (එසේ නොමැති නම් එකම ඒකාබද්ධ කළ යුතුය) සහ ආරෝහණ අනුපිළිවෙලින් සකස් කර ඇති බව අපි උපකල්පනය කරමු. විවික්ත අහඹු විචල්‍යයක සම්පූර්ණ ගුනාංගීකරනය සඳහා එහි සියලු අගයන් පමණක් නොව, සම්භාවිතාවන් ද ලබා දිය යුතුය
විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නියමය
ඕනෑම රීතියක් (කාර්යය, වගුව) ලෙස හැඳින්වේ පි(x), අහඹු විචල්‍යයක් හා සම්බන්ධ සියලුම ආකාරයේ සිදුවීම්වල සම්භාවිතාව සොයා ගැනීමට ඔබට ඉඩ සලසයි (නිදසුනක් ලෙස, එය යම් අගයක උදාහරණයක් හෝ යම් පරතරයකට වැටීමේ සම්භාවිතාව). විවික්ත අහඹු විචල්‍යයක් සඳහා වඩාත් සරල සහ පහසු බෙදාහැරීමේ නීතිය පහත වගුවේ ආකාරයෙන් දක්වා ඇත: එවැනි වගුවක් ලෙස හැඳින්වේ විවික්ත අහඹු විචල්‍යයක ව්යාප්තිය ආසන්නයේ. බෙදාහැරීමේ ශ්‍රේණියේ ඉහළ පේළිය විවික්ත සසම්භාවී විචල්‍යයක (x) හැකි සියලුම අගයන් ආරෝහණ අනුපිළිවෙලින් ලැයිස්තුගත කරයි, සහ පහළ රේඛාව මෙම අගයන්හි සම්භාවිතා ලැයිස්තුගත කරයි ( පි). සංවර්ධන උදාහරණ 1ශිෂ්‍ය කණ්ඩායම තුළ ලොතරැයියක් සංවිධානය කරන ලදී. රූබල් 1000 ක් වටිනා දේවල් දෙකක් සෙල්ලම් කරයි. සහ එකක මිල රුබල් 3000 කි. රූබල් 100 ක් සඳහා එක් ටිකට්පතක් මිලදී ගත් ශිෂ්‍යයෙකු සඳහා ශුද්ධ ජයග්‍රහණ ප්‍රමාණය බෙදා හැරීමේ නීතිය අඳින්න. ප්‍රවේශපත්‍ර 50ක් විකුණා ඇත. විසඳුමක්. අප උනන්දු වන අහඹු විචල්යය xඅගයන් තුනක් ගත හැක: - 100 rubles. (ශිෂ්‍යයා ජයග්‍රහණය නොකරන්නේ නම්, නමුත් ඇත්ත වශයෙන්ම ඔහු ටිකට් සඳහා ගෙවූ රූබල් 100 ක් අහිමි වුවහොත්), රූබල් 900 ක්. සහ රූබල් 2900 ක්. (සැබෑ ජයග්‍රහණ රුබල් 100 කින් අඩු වේ - ටිකට් පතේ පිරිවැය). පළමු ප්රතිඵලය 50 න් 47 කින් ද, දෙවැන්න 2 කින් ද, තෙවනුව එකකින් ද අනුග්‍රහය දක්වයි. එබැවින් ඔවුන්ගේ සම්භාවිතාවන්: පී(x=-100)=47/50=0,94
,
පී(x=900)=2/50=0,04
,
පී(x=2900)=1/50=0,02
. විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නීතිය xආකෘතිය ඇත බෙදාහැරීමේ ශ්‍රේණියක් සෑදිය හැක්කේ විවික්ත අහඹු විචල්‍යයක් සඳහා පමණි (විවික්ත නොවන එකක් සඳහා එය ගොඩනැගිය නොහැක, එවැනි අහඹු විචල්‍යයක විය හැකි අගයන් සමූහය ගණන් කළ නොහැකි නිසා පමණක් නම්, ඒවා ඉහළින් ලැයිස්තුගත කළ නොහැක. මේසයේ රේඛාව). සියලුම අහඹු විචල්යයන් සඳහා (විවික්ත සහ විවික්ත නොවන) සුදුසු බෙදාහැරීමේ නීතියේ වඩාත් සාමාන්ය ආකාරය වන්නේ බෙදා හැරීමේ ශ්‍රිතයයි. විවික්ත අහඹු විචල්‍යයක ව්‍යාප්ති ශ්‍රිතයහෝ අනුකලිත කාර්යයශ්රිතයක් ලෙස හැඳින්වේ ඕනෑම විවික්ත සසම්භාවී විචල්‍යයක බෙදා හැරීමේ ශ්‍රිතය අඛණ්ඩ පියවර ශ්‍රිතයක් වන අතර එහි පැනීම් සසම්භාවී විචල්‍යයේ විය හැකි අගයන්ට අනුරූප වන අතර මෙම අගයන්හි සම්භාවිතාවන්ට සමාන වේ. උදාහරණ 2විවික්ත අහඹු විචල්යය xඩයි එකක් විසි කිරීමෙන් ලබාගත් ලකුණු ගණනයි. එහි බෙදා හැරීමේ කාර්යය ගොඩනඟන්න. විසඳුමක්. විවික්ත අහඹු විචල්‍යයක බෙදාහැරීමේ ශ්‍රේණිය xපෙනෙන්නේ: බෙදා හැරීමේ කාර්යය එෆ්(x) විශාලත්වයෙන් 1/6 ට සමාන පැනීම් 6 ක් ඇත (පහත රූපයේ). උදාහරණය 3බඳුනක සුදු බෝල 6 ක් සහ කළු බෝල 4 ක් අඩංගු වේ. බඳුනෙන් බෝල 3 ක් ගනු ලැබේ. ඇද ගන්නා ලද බෝල අතර ඇති සුදු බෝල ගණන විවික්ත අහඹු විචල්යයකි x. එයට අනුරූප බෙදාහැරීමේ නීතිය සම්පාදනය කරන්න. x 0, 1, 2, 3 අගයන් ගත හැක. ඒවාට අනුරූප වන සම්භාවිතාවන් වඩාත් පහසුවෙන් ගණනය කළ හැක සම්භාවිතා ගුණ කිරීමේ රීතිය. විවික්ත අහඹු විචල්‍යයක් සඳහා අපි පහත බෙදාහැරීමේ නීතිය ලබා ගනිමු: උදාහරණය 4විවික්ත අහඹු විචල්‍යයක් සඳහා බෙදා හැරීමේ නීතියක් සම්පාදනය කරන්න - එක් පහරකින් පහර දීමේ සම්භාවිතාව 0.1 නම්, පහර හතරකින් ඉලක්කයට එල්ල වන පහර ගණන. විසඳුමක්. විවික්ත අහඹු විචල්යය xවිවිධ අගයන් පහක් ගත හැක: 1, 2, 3, 4, 5. අපි අනුරූප සම්භාවිතාවන් සොයන්නෙමු බර්නූලි සූත්රය
n = 4
, පි = 1,1
, q = 1 - පි = 0,9
, එම් = 0, 1, 2, 3, 4
අපට ලැබෙනවා එබැවින්, විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නියමය xආකෘතිය ඇත විවික්ත අහඹු විචල්‍යයක අගයන්හි සම්භාවිතාව බර්නූලි සූත්රය මගින් තීරණය කළ හැකි නම්, අහඹු විචල්‍යයට ඇත්තේ ද්විපද ව්යාප්තිය . අත්හදා බැලීම් ගණන ප්‍රමාණවත් නම්, මෙම අත්හදා බැලීම් වලදී උනන්දුවක් දක්වන සිදුවීම හරියටම සිදු වීමේ සම්භාවිතාව එම්කාලය, නීතියට කීකරු වන්න විෂ බෙදා හැරීම . විවික්ත අහඹු විචල්‍යයක ව්‍යාප්ති ශ්‍රිතය ගණනය කිරීමට එෆ්(x), මායිම් අගයට වඩා අඩු හෝ සමාන වන සියලුම අගයන් වල සම්භාවිතා එකතු කිරීම අවශ්‍ය වේ. x. උදාහරණ 5විවාහයේ කාලසීමාව මත වර්ෂය තුළ විසුරුවා හරින ලද විවාහ සංඛ්යාව මත යැපීම පිළිබඳ දත්ත වගුවේ අඩංගු වේ. ඊළඟ දික්කසාද විවාහය වසර 5කට අඩු හෝ ඊට සමාන වූ සම්භාවිතාව සොයන්න. විසඳුමක්. සම්භාවිතාව ගණනය කරනු ලබන්නේ අදාළ දික්කසාද විවාහ සංඛ්යාව සම්පූර්ණ අංක 6010 න් බෙදීමෙනි. මීළඟ දික්කසාද විවාහය වසර 5ක් පැවතීමේ සම්භාවිතාව 0.056 කි. ඊළඟ දික්කසාද විවාහයේ කාලසීමාව අවුරුදු 5 ට අඩු හෝ සමාන වීමේ සම්භාවිතාව 0.186 ට සමාන වේ. අපි එය ලබා ගත්තේ අගය එකතු කිරීමෙනි එෆ්(x) වසර 4 ක කාලයක් සහිත විවාහ සඳහා, ඇතුළුව, අවුරුදු 5 ක කාල සීමාවක් සහිත විවාහ සඳහා සම්භාවිතාව. බොහෝ විට විවික්ත අහඹු විචල්‍යයක සියලුම අගයන් නොදනී, නමුත් ශ්‍රේණියේ සමහර අගයන් හෝ සම්භාවිතාවන් දනී. අහඹු විචල්‍යයක ගණිතමය අපේක්ෂාව සහ (හෝ) විචලනයවෙනම පාඩමක් වෙන් කර ඇත. විවික්ත අහඹු විචල්‍යයක් බෙදා හැරීමේ නීතිය සැකසීමේදී සහ එවැනි ගැටළු විසඳීමේ උදාහරණ විශ්ලේෂණය කිරීමේදී උපකාර කළ හැකි මෙම පාඩමෙන් සූත්‍ර කිහිපයක් මෙන්න. විවික්ත සසම්භාවී විචල්‍යයක ගණිතමය අපේක්ෂාව යනු එහි ඇති හැකි සියලුම අගයන්හි නිෂ්පාදනවල එකතුව සහ මෙම අගයන්හි සම්භාවිතාවයි: නිර්වචනය අනුව විවික්ත අහඹු විචල්‍යයක් විසුරුවා හැරීම සඳහා වන සූත්රය වන්නේ: බොහෝ විට පහත විචල්‍ය සූත්රය ගණනය කිරීම් සඳහා වඩාත් පහසු වේ: කොහෙද උදාහරණය 6විවික්ත අහඹු විචල්යය xඅගයන් දෙකක් පමණක් ගත හැක. එය සම්භාවිතාව සමඟ කුඩා අගය ගනී පි= 0.6. විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නියමය සොයන්න x, එහි ගණිතමය අපේක්ෂාව සහ විචලනය බව දන්නේ නම්. විසඳුමක්. අහඹු විචල්‍යයක් විශාල අගයක් ගන්නා සම්භාවිතාව x2
, 1 - 0.6 = 4 ට සමාන වේ. ගණිතමය අපේක්ෂාවේ සූත්රය (1) භාවිතා කරමින්, අපි නොදන්නා දේ අපගේ විවික්ත අහඹු විචල්‍යයේ අගයන් වන සමීකරණයක් සම්පාදනය කරන්නෙමු: විසරණයේ සූත්රය (2) භාවිතා කරමින්, අපි තවත් සමීකරණයක් සම්පාදනය කරමු, එහි නොදන්නා දේ විවික්ත අහඹු විචල්‍යයක අගයන් ද වේ: ලබාගත් සමීකරණ දෙකක පද්ධතිය ආදේශන ක්රමය මගින් විසඳන්න. පළමු සමීකරණයෙන් අපට ලැබේ මෙම ප්රකාශනය දෙවන සමීකරණයට ආදේශ කිරීම, සරල පරිවර්තනයන්ගෙන් පසුව, අපි ලබා ගනිමු චතුරස්රාකාර සමීකරණය මූල දෙකක් ඇත: 7/5 සහ −1 . පළමු මූලය ගැටලුවේ කොන්දේසි සපුරාලන්නේ නැත x2
< x 1
. මේ අනුව, විවික්ත අහඹු විචල්‍යයකට ගත හැකි අගයන් xඅපගේ උදාහරණයේ කොන්දේසි අනුව, සමාන වේ x1
= −1
හා x2
= 2
. විවික්ත අහඹු විචල්‍යයක බෙදාහැරීමේ මාලාවක් ලබා දී ඇත. නැතිවූ සම්භාවිතාව සොයාගෙන බෙදා හැරීමේ කාර්යය සැලසුම් කරන්න. මෙම අගයේ ගණිතමය අපේක්ෂාව සහ විචලනය ගණනය කරන්න. සසම්භාවී විචල්‍ය X ලබා ගන්නේ අගයන් හතරක් පමණි: -4, -3, 1 සහ 2. එය මෙම එක් එක් අගයන් යම් සම්භාවිතාවක් සහිතව ගනී. සියලු සම්භාවිතාවන්හි එකතුව 1 ට සමාන විය යුතු බැවින්, අතුරුදහන් වූ සම්භාවිතාව සමාන වේ: 0,3 + ? + 0,1 + 0,4 = 1, සසම්භාවී විචල්‍ය X හි ව්‍යාප්ති ශ්‍රිතය සම්පාදනය කරන්න. බෙදාහැරීමේ ශ්‍රිතය , එවිට: ප්රතිඵලයක් වශයෙන්, අපි කාර්යය සැලසුම් කරමු එෆ්(x)
. විවික්ත සසම්භාවී විචල්‍යයක ගණිතමය අපේක්ෂාව අහඹු විචල්‍යයේ අගය සහ ඊට අනුරූප සම්භාවිතාවේ නිෂ්පාදනවල එකතුවට සමාන වේ, i.e. විවික්ත අහඹු විචල්‍යයක විචලනය සූත්රය මගින් සොයා ගැනේ: මෙන්න: - අංකයක සාධක සිදුවීමක් යනු අත්දැකීමක ප්රතිඵලයක් ලෙස සිදු විය හැකි හෝ සිදු නොවන ඕනෑම කරුණකි. සිදුවීම් ඒකාබද්ධ කිරීම නමුත්හා හිදී- මෙම සිදුවීම සිට, පෙනුමෙන් හෝ සිදුවීමෙන් සමන්විත වේ නමුත්, හෝ සිදුවීම් හිදී, හෝ සිදුවීම් දෙකම එකවර. තනතුර: සිදුවීම් ඡේදනය නමුත්හා හිදී- මෙම සිදුවීම සිට, සිදුවීම් දෙකෙහිම එකවර සිදුවීමෙන් සමන්විත වේ. තනතුර: සිදුවීම් සම්භාවිතාව නමුත්අත්හදා බැලීම් ගණනෙහි අනුපාතය වේ සිදුවීම් සම්භාවිතාව සිදුවීම් A සහ B ස්වාධීන නම් (එකක් සිදුවීම අනෙකක් සිදුවීමට බලපාන්නේ නැත), එවිට සිදුවීමේ සම්භාවිතාව: සිදුවීම් සම්භාවිතාව සිදුවීම් සම්භාවිතාව නමුත්, සිදුවීම් සම්භාවිතාව හිදී, සිදුවීම් A සහ B නොගැලපේ නම් (ඒවා එකවර සිදු විය නොහැක), එවිට සිදුවීමේ සම්භාවිතාව: සිදුවීමට ඉඩ දෙන්න නමුත්එක් සිදුවීමක් සමඟ එකවර සිදු විය හැක ස්වාධීන පරීක්ෂණ සිදු කිරීමට ඉඩ දෙන්න. සිදුවීමක් සිදුවීමේ (සාර්ථකත්වය) සම්භාවිතාව නමුත්ඒ සෑම එකක් තුළම නියත හා සමාන වේ පි, අසාර්ථක වීමේ සම්භාවිතාව (එනම්, සිදුවීමක් සිදුවීම නොවේ නමුත්) q
=
1 - පි. එවිට සිදුවීමේ සම්භාවිතාව කේතුළ සාර්ථකත්වය nපරීක්ෂණ බර්නූලි සූත්රය මගින් සොයාගත හැකිය: බොහෝ දුරට සාර්ථකත්වයන් ගණන විවික්ත අඛණ්ඩ (උදා, දරුවන් 5 දෙනෙකු සිටින පවුලක ගැහැණු ළමුන් සංඛ්යාව) (උදා, කේතලය වැඩ කරන වේලාව) බෙදාහැරීමේ ශ්‍රේණියක් මඟින් විවික්ත අගය ලබා දීමට ඉඩ දෙන්න: , , ..., - අහඹු විචල්‍යයක අගයන් x; , , ..., අනුරූප සම්භාවිතාවන් වේ. අහඹු විචල්‍යයක ව්‍යාප්ති ශ්‍රිතය xසම්පූර්ණ සංඛ්යා රේඛාව මත ලබා දී ඇති ශ්‍රිතයක් ලෙස හඳුන්වනු ලබන අතර එම සම්භාවිතාවට සමාන වේ xඅඩු වනු ඇත x: සිදුවීම. අහඹු සිදුවීම් මත මෙහෙයුම්. සිදුවීමක සම්භාවිතාව පිළිබඳ සංකල්පය. සම්භාවිතාව එකතු කිරීම සහ ගුණ කිරීම පිළිබඳ නීති. කොන්දේසි සහිත සම්භාවිතාව. සම්පූර්ණ සම්භාවිතා සූත්රය. බේස් සූත්රය. බර්නූලි යෝජනා ක්රමය. සසම්භාවී විචල්යය, එහි ව්‍යාප්ති ශ්‍රිතය සහ බෙදාහැරීමේ ශ්‍රේණිය. බෙදා හැරීමේ කාර්යයේ මූලික ගුණාංග. අපේක්ෂිත අගය. ගණිතමය අපේක්ෂාවේ ගුණාංග. විසුරුම. විසරණ ගුණාංග. ඒකමාන අහඹු විචල්‍යයක සම්භාවිතා ව්යාප්තිය ඝනත්වය. බෙදා හැරීම් වර්ග: ඒකාකාර, ඝාතීය, සාමාන්ය, ද්විපද සහ විෂ ව්යාප්තිය. Moivre-Laplace හි දේශීය සහ සමෝධානික සිද්ධාන්ත. අහඹු විචල්‍ය දෙකක පද්ධතියක නීතිය සහ බෙදා හැරීමේ කාර්යය. අහඹු විචල්‍ය දෙකක පද්ධතියක ව්‍යාප්ති ඝනත්වය. බෙදා හැරීමේ කොන්දේසි සහිත නීති, කොන්දේසි සහිත ගණිතමය අපේක්ෂාව. යැපෙන සහ ස්වාධීන අහඹු විචල්යයන්. සහසම්බන්ධතා සංගුණකය. නියැදිය. නියැදි සැකසීම. බහුඅස්ර සහ සංඛ්යාත හිස්ටෝග්රෑම්. ආනුභවික බෙදා හැරීමේ කාර්යය. බෙදාහැරීමේ පරාමිතීන් තක්සේරු කිරීමේ සංකල්පය. තක්සේරු අවශ්යතා. විශ්වාස පරතරය. ගණිතමය අපේක්ෂාව සහ සම්මත අපගමනය තක්සේරු කිරීම සඳහා පරතරයන් ගොඩනැගීම. සංඛ්යාන උපකල්පන. එකඟතා නිර්ණායක. සම්භාවිතා න්‍යායේ යෙදීම් වලදී, අත්හදා බැලීමේ ප්‍රමාණාත්මක ගුනාංගීකරනය මූලික වැදගත්කමක් දරයි. ප්‍රමාණාත්මකව තීරණය කළ හැකි සහ අත්හදා බැලීමක ප්රතිඵලයක් ලෙස, නඩුව අනුව විවිධ අගයන් ලබා ගත හැකි ප්‍රමාණය ලෙස හැඳින්වේ. අහඹු විචල්‍යයක්. අහඹු විචල්‍ය සඳහා උදාහරණ: 1. දාදු කැටයක විසි කිරීම් දහයක ඉරට්ටේ ලක්ෂ්‍ය සංඛ්යාවක් ඇති වූ සංඛ්යාව. 2. වෙඩි තැබීම් මාලාවක් එල්ල කරන වෙඩික්කරු විසින් ඉලක්කයට එල්ල කරන පහර ගණන. 3. පිපිරෙන ප්‍රක්ෂේපණයක කොටස් ගණන. ඉහත එක් එක් උදාහරණය තුළ, අහඹු විචල්‍යයකට ගත හැක්කේ හුදකලා අගයන් පමණි, එනම් ස්වාභාවික සංඛ්යා මාලාවක් භාවිතයෙන් ගණනය කළ හැකි අගයන්. එවැනි අහඹු විචල්‍යයක්, මෙම විචල්යය යම් සම්භාවිතාවන් සමඟ ගන්නා වෙනම හුදකලා සංඛ්යා විය හැකි අගයන් ලෙස හැඳින්වේ. විවික්ත. විවික්ත අහඹු විචල්‍යයක විය හැකි අගයන් සංඛ්යාව පරිමිත හෝ අනන්ත (ගණන් කළ හැකි) විය හැක. බෙදාහැරීමේ නීතියවිවික්ත අහඹු විචල්‍යයක් එහි විය හැකි අගයන් සහ ඒවාට අනුරූප සම්භාවිතා ලැයිස්තුවක් ලෙස හැඳින්වේ. විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නියමය වගුවක (සම්භාවිතා බෙදාහැරීමේ ශ්‍රේණි), විශ්ලේෂණාත්මකව සහ ප්‍රස්ථාරිකව (සම්භාවිතා ව්යාප්තිය බහුඅස්රය) ආකාරයෙන් දැක්විය හැක. මෙම හෝ එම අත්හදා බැලීම සිදු කරන විට, "සාමාන්යයෙන්" අධ්‍යයනය යටතේ ඇති අගය තක්සේරු කිරීම අවශ්‍ය වේ. සසම්භාවී විචල්‍යයක සාමාන්ය අගයේ කාර්යභාරය ඉටු කරනු ලබන්නේ සංඛ්යාත්මක ලක්ෂණයක් ලෙසිනි ගණිතමය අපේක්ෂාව,සූත්රය මගින් අර්ථ දක්වා ඇත කොහෙද x 1 , x 2
,.. , x n- සසම්භාවී විචල්‍යයක අගයන් x, ඒ පි 1 ,පි 2 ,
... , පි nමෙම අගයන්හි සම්භාවිතාවන් වේ (එය සලකන්න පි 1
+
පි 2
+…+
පි n =
1). උදාහරණයක්. වෙඩි තැබීම ඉලක්කයට සිදු කෙරේ (රූපය 11). I හි පහරක් ලකුණු තුනක් ලබා දෙයි, II - ලකුණු දෙකක්, III හි - එක් ලක්ෂයක්. එක් වෙඩික්කරුවෙකු විසින් එක් පහරකින් දැවී ගිය ලකුණු ගණනට පෝරමයේ බෙදා හැරීමේ නීතියක් ඇත වෙඩික්කරුවන්ගේ දක්ෂතාවය සංසන්දනය කිරීම සඳහා, ලබාගත් ලකුණුවල සාමාන්ය අගයන් සංසන්දනය කිරීම ප්‍රමාණවත් වේ, i.e. ගණිතමය අපේක්ෂාවන් එම්(x) හා එම්(වයි):
එම්(x)
=
1
0,4
+ 2
0,2
+ 3
0,4
= 2,0, එම්(වයි)
=
1
0,2
+ 2
0,5
+ 3
0,3
= 2,1. දෙවන වෙඩික්කරු සාමාන්යයෙන් තරමක් වැඩි ලකුණු සංඛ්යාවක් ලබා දෙයි, i.e. නැවත නැවතත් වෙඩි තැබීම සමඟ, එය හොඳම ප්රතිඵලය ලබා දෙනු ඇත. ගණිතමය අපේක්ෂාවේ ගුණාංග සටහන් කරන්න: 1. නියත අගයක ගණිතමය අපේක්ෂාව නියතයටම සමාන වේ: එම්(සී)
= සී. 2. සසම්භාවී විචල්‍යවල එකතුවේ ගණිතමය අපේක්ෂාව පදවල ගණිතමය අපේක්ෂාවල එකතුවට සමාන වේ: M=(x 1 +
x 2 +…+
x n)=
එම්(x 1)+
එම්(x 2)+…+
එම්(x n). 3. අන්‍යෝන්‍ය වශයෙන් ස්වාධීන අහඹු විචල්‍යවල ගුණිතයේ ගණිතමය අපේක්ෂාව සාධකවල ගණිතමය අපේක්ෂාවන්ගේ ගුණිතයට සමාන වේ. එම්(x 1 x 2 …
x n)
=
එම්(x 1)එම්(x 2)…
එම්(x n). 4. ද්විපද ව්‍යාප්තියේ ගණිතමය නිෂේධනය අත්හදා බැලීම් ගණනේ ගුණිතයට සමාන වන අතර එක් අත්හදා බැලීමක සිදුවීමක සම්භාවිතාව (කාර්යය 4.6). එම්(x)
= pr. අහඹු විචල්‍යයක් "සාමාන්යයෙන්" එහි ගණිතමය අපේක්ෂාවෙන් බැහැර වන ආකාරය තක්සේරු කිරීමට, i.e. සම්භාවිතා න්‍යායේ අහඹු විචල්‍යයක අගයන් පැතිරීම සංලක්ෂිත කිරීම සඳහා, විසරණය යන සංකල්පය භාවිතා වේ. විසුරුමඅහඹු විචල්යය xවර්ග අපගමනයෙහි ගණිතමය අපේක්ෂාව ලෙස හැඳින්වේ: ඩී(x)
=
එම්[(x
-
එම්(x)) 2 ]. විසරණය යනු අහඹු විචල්‍යයක විසරණයේ සංඛ්යාත්මක ලක්ෂණයකි. සසම්භාවී විචල්‍යයක විචලනය කුඩා වන තරමට එහි විය හැකි අගයන් ගණිතමය අපේක්ෂාව වටා පිහිටා ඇති බව අර්ථ දැක්වීමෙන් දැකිය හැකිය, එනම් අහඹු විචල්‍යයේ අගයන් එහි ගණිතමය ගුණයෙන් සංලක්ෂිත වේ. අපේක්ෂාව. විචලනය සූත්රය මගින් ගණනය කළ හැකි බව අර්ථ දැක්වීමෙන් එය අනුගමනය කරයි වෙනත් සූත්‍රයක් භාවිතයෙන් විසරණය ගණනය කිරීම පහසුය: ඩී(x)
=
එම්(x 2)
- (එම්(x)) 2 .
විසුරුවා හැරීමට පහත ගුණාංග ඇත: 1. නියතයේ විසරණය ශුන්‍ය වේ: ඩී(සී)
=
0.
2. වර්ග කිරීම මගින් විසරණ ලකුණෙන් නියත සාධකයක් ගත හැක: ඩී(CX)
=
සී 2 ඩී(x). 3. ස්වාධීන අහඹු විචල්‍යවල එකතුවේ විචලනය නියමවල විචල්‍යයේ එකතුවට සමාන වේ: ඩී(x 1 +
x 2 +
x 3 +…+
x n)=
ඩී(x 1)+
ඩී(x 2)+…+
ඩී(x n) 4. ද්විපද ව්‍යාප්තියේ විචලනය අත්හදා බැලීම් සංඛ්‍යාවේ ගුණිතයට සමාන වන අතර එක් අත්හදා බැලීමක සිදුවීමක් සිදුවීමේ සහ සිදුනොවීමේ සම්භාවිතාව: ඩී(x)
= npq. සම්භාවිතා න්‍යායේ දී, සංඛ්යාත්මක ලක්ෂණයක් බොහෝ විට භාවිතා වේ, එය අහඹු විචල්‍යයක විචල්‍යයේ වර්ගමූලයට සමාන වේ. මෙම සංඛ්යාත්මක ලක්ෂණය සම්මත අපගමනය ලෙස හැඳින්වෙන අතර එය සංකේතයෙන් දැක්වේ එය සසම්භාවී විචල්‍යයක සාමාන්ය අගයෙන් අපගමනය වීමේ ආසන්න ප්‍රමාණය සංලක්ෂිත වන අතර අහඹු විචල්‍යයට සමාන මානයක් ඇත. 4.1.
වෙඩික්කරු ඉලක්කයට වෙඩි තුනක් එල්ල කරයි. සෑම පහරකින්ම ඉලක්කයට පහර දීමේ සම්භාවිතාව 0.3 කි. පහර ගණන බෙදාහැරීමේ මාලාවක් සාදන්න. විසඳුමක්. පහර ගණන විවික්ත අහඹු විචල්යයකි x. එක් එක් අගය x n
අහඹු විචල්යය xයම් සම්භාවිතාවකට අනුරූප වේ පී n . මෙම නඩුවේ විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ නියමය සැකසිය හැක ආසන්න බෙදා හැරීම. මෙම කාර්යයේදී x 0, 1, 2, 3 අගයන් ගනී. බර්නූලි සූත්‍රයට අනුව සසම්භාවී විචල්‍යයේ හැකි අගයන්හි සම්භාවිතාව සොයා ගන්න: ආර් 3 (0)
= (0,7) 3 =
0,343, ආර් 3 (1)
= ආර් 3 (2)
= ආර් 3 (3)
= (0,3) 3 =
0,027. සසම්භාවී විචල්‍යයේ අගයන් සකසා තිබීම xආරෝහණ අනුපිළිවෙලින්, අපි බෙදාහැරීමේ මාලාව ලබා ගනිමු: x n එකතුව බව සලකන්න යන්නෙන් අදහස් වන්නේ සසම්භාවී විචල්‍යයේ සම්භාවිතාවයි xහැකි අය අතරින් අවම වශයෙන් එක් අගයක් ගනු ඇත, එබැවින් මෙම සිදුවීම නිසැක ය 4.2
.1 සිට 4 දක්වා අංක සහිත බෝල හතරක් බඳුනේ ඇත. බෝල දෙකක් පිටතට ගනු ලැබේ. අහඹු අගය xයනු බෝලවල සංඛ්යා එකතුවයි. අහඹු විචල්‍යයක බෙදාහැරීමේ ශ්‍රේණියක් සාදන්න x. විසඳුමක්.අහඹු විචල්‍යයක අගයන් x 3, 4, 5, 6, 7 වේ. අනුරූප සම්භාවිතා සොයන්න. අගය 3 සසම්භාවී විචල්යය xතෝරාගත් බෝල වලින් එකක අංක 1 සහ අනෙක් 2 ඇති එකම අවස්ථාවෙහිදී ගත හැක. පරීක්ෂණයේ ඇති විය හැකි ප්රතිඵල සංඛ්යාව හතරක (හැකි බෝල යුගල ගණන) දෙකකින් සංයෝජන ගණනට සමාන වේ. සම්භාව්ය සම්භාවිතා සූත්රය අනුව, අපි ලබා ගනිමු එලෙසම, ආර්(x= 4) =ආර්(x= 6) =ආර්(x= 7) = 1/6. එකතුව 5 අවස්ථා දෙකකින් දිස්විය හැක: 1 + 4 සහ 2 + 3, එසේ xපෙනෙන්නේ: බෙදා හැරීමේ කාර්යය සොයන්න එෆ්(x) සසම්භාවී විචල්යය xසහ එය කුමන්ත්රණය කරන්න. සඳහා ගණනය කරන්න xඑහි ගණිතමය අපේක්ෂාව සහ විචලනය. විසඳුමක්. අහඹු විචල්‍යයක ව්‍යාප්ති නියමය බෙදා හැරීමේ ශ්‍රිතය මගින් ලබා දිය හැක එෆ්(x)
=පී(x
x).
බෙදා හැරීමේ කාර්යය එෆ්(x) යනු සම්පූර්ණ සැබෑ අක්ෂය මත අර්ථ දක්වා ඇති අඩු නොවන, වම්-අඛණ්ඩ ශ්‍රිතයකි. එෆ්
(-
)=
0,එෆ්
(+
)=
1. විවික්ත අහඹු විචල්‍යයක් සඳහා, මෙම ශ්‍රිතය සූත්රය මගින් ප්‍රකාශ වේ එබැවින්, මෙම නඩුවේදී බෙදාහැරීමේ කාර්යය කුමන්ත්රණය එෆ්(x) යනු පියවර රේඛාවකි (රූපය 12) එෆ්(x) අපේක්ෂිත අගයඑම්(x) යනු අගයන්හි බරිත සාමාන්‍යය වේ x 1 , X 2 ,……X nඅහඹු විචල්යය xබර සමඟ ρ
1,
ρ
2, ……
, ρ
n
සහ සසම්භාවී විචල්‍යයේ මධ්‍යන්‍ය අගය ලෙස හැඳින්වේ x. සූත්රය අනුව එම්(x)= x 1
ρ
1 + x 2
ρ
2 +……+ x n
ρ
n එම්(x) = 3 0.14 + 5 0.2 + 7 0.49 + 11 0.17 = 6.72. විසුරුමඅහඹු විචල්‍යයක අගයන් එහි සාමාන්ය අගයෙන් විසරණය වීමේ මට්ටම සංලක්ෂිත වන අතර එය දක්වනු ලැබේ ඩී(x): ඩී(x)= එම්[(එච්.එම්(x)) 2 ]= එම්(x 2)
–[එම්(x)] 2 . විවික්ත අහඹු විචල්‍යයක් සඳහා, විචලනයට ස්වරූපය ඇත නැතහොත් එය සූත්රය මගින් ගණනය කළ හැක ගැටලුවේ සංඛ්යාත්මක දත්ත සූත්‍රයට ආදේශ කිරීමෙන් අපට ලැබෙන්නේ: එම්(x 2)
=
3 2
∙ 0,14+5 2
∙ 0,2+7 2
∙ 0,49+11 2
∙ 0,17 = 50,84 ඩී(x)
= 50,84-6,72 2
= 5,6816. 4.4.
ඩයිස් දෙකක් එකවරම දෙවරක් විසි කරයි. විවික්ත අහඹු විචල්‍යයක් සඳහා ද්විපද ව්‍යාප්ති නියමයක් ලියන්න x- දාදු කැට දෙකක ඉරට්ටේ මුළු ලකුණු සංඛ්‍යාවක සිදුවීම් ගණන. විසඳුමක්. අපි අහඹු සිදුවීමක් සලකා බලමු නමුත්= (එක් විසි කිරීමකදී දාදු කැට දෙකක් මත, මුළු ලකුණු සංඛ්යාව ඉරට්ටේ වැටුණි). සම්භාවිතාව පිළිබඳ සම්භාව්ය අර්ථ දැක්වීම භාවිතා කරමින්, අපි සොයා ගනිමු ආර්(නමුත්)=
කොහෙද n
- පරීක්ෂණයේ ඇති විය හැකි ප්රතිඵල සංඛ්යාව රීතිය මගින් සොයාගත හැකිය ගුණ කිරීම්: n
= 6∙6 =36, එම්
-
හිතකර සිදුවීම් ගණන නමුත්ප්රතිඵල - සමාන එම්= 3∙6=18. මේ අනුව, එක් අත්හදා බැලීමක සාර්ථකත්වයේ සම්භාවිතාව වේ ρ
= පී(නමුත්)=
1/2.
බර්නූලි පරීක්ෂණ යෝජනා ක්රමය භාවිතයෙන් ගැටළුව විසඳනු ලැබේ. මෙහි එක් අභියෝගයක් වන්නේ එක් වරක් කැට දෙකක් පෙරළීමයි. එවැනි පරීක්ෂණ ගණන n
= 2. සසම්භාවී විචල්යය xසම්භාවිතාවන් සමඟ 0, 1, 2 අගයන් ගනී ආර් 2 (0)
= අහඹු විචල්‍යයක අපේක්ෂිත ද්විපද ව්යාප්තිය xබෙදාහැරීමේ මාලාවක් ලෙස නිරූපණය කළ හැක: x n ρ
n 4.5
. කොටස් හයකින් යුත් කණ්ඩායමක සම්මත කොටස් හතරක් ඇත. අයිතම තුනක් අහඹු ලෙස තෝරා ගන්නා ලදී. විවික්ත අහඹු විචල්‍යයක සම්භාවිතා ව්යාප්තිය සම්පාදනය කරන්න x- තෝරාගත් ඒවා අතර සම්මත කොටස් ගණන සහ එහි ගණිතමය අපේක්ෂාව සොයා ගන්න. විසඳුමක්.අහඹු විචල්‍යයක අගයන් xඅංක 0,1,2,3 වේ. ඒක පැහැදිලියි ආර්(x=0)=0, සම්මත නොවන කොටස් දෙකක් පමණක් ඇති බැවින්. ආර්(x=1) = ආර්(X= 2) = ආර්(x=3) = අහඹු විචල්‍යයක බෙදා හැරීමේ නීතිය xබෙදාහැරීමේ මාලාවක් ලෙස නියෝජනය කරන්න: x n ρ
n අපේක්ෂිත අගය එම්(x)=1
∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2. 4.6
. විවික්ත අහඹු විචල්‍යයක ගණිතමය අපේක්ෂාව බව ඔප්පු කරන්න x- සිදුවීමේ සිදුවීම් ගණන නමුත්තුල nස්වාධීන පරීක්ෂණ, ඒ සෑම එකක් තුළම සිදුවීමක් සිදුවීමේ සම්භාවිතාව සමාන වේ ρ
- එක් අත්හදා බැලීමක සිදුවීමක සම්භාවිතාව මගින් අත්හදා බැලීම් ගණනේ ගුණිතයට සමාන වේ, එනම් ද්විපද ව්‍යාප්තියේ ගණිතමය අපේක්ෂාව බව ඔප්පු කිරීමට එම්(x)
=n .
ρ
, විචලනය අතරතුර ඩී(x)
=np
. විසඳුමක්.අහඹු අගය x 0, 1, 2 අගයන් ගත හැක..., n. සම්භාවිතාව ආර්(x= k) බර්නූලි සූත්රය මගින් සොයා ගැනේ: ආර්(x=k)= ආර් n(k)= සසම්භාවී විචල්‍ය බෙදා හැරීම් මාලාව xපෙනෙන්නේ: x n ρ
n q n කොහෙද q=
1-
ρ
. ගණිතමය අපේක්ෂාව සඳහා, අපට ප්රකාශනය ඇත: එම්(x)= එක් පරීක්ෂණයකදී, එනම්, සමඟ n=අහඹු විචල්‍යයක් සඳහා 1 x 1 - සිදුවීමේ සිදුවීම් ගණන නමුත්- බෙදාහැරීමේ මාලාවට පෝරමය ඇත: x n ρ
n එම්(x 1)=
0 q +
1
∙ පි
=
පි ඩී(x 1)
=
පි
–
පි 2
=
පි(1-
පි)
=
pq. අ x k - සිදුවීමේ සිදුවීම් ගණන නමුත්කුමන පරීක්ෂණයේදී, එවිට ආර්(x වෙත)=
ρ
හා X=X 1 +X 2 +....+X n . මෙතනින් අපිට ලැබෙනවා එම්(x)= එම්(x 1
)+ එම්(x 2)+
… + එම්(x n)=
nρ,
ඩී(x)=D(x 1)+D(x 2)+
...
+D(x n)=npq. 4.7.
QCD ප්‍රමිතිකරණය සඳහා නිෂ්පාදන පරීක්ෂා කරයි. අයිතමය සම්මත වීමේ සම්භාවිතාව 0.9 කි. සෑම කණ්ඩායමකම අයිතම 5 ක් අඩංගු වේ. විවික්ත අහඹු විචල්‍යයක ගණිතමය අපේක්ෂාව සොයන්න x- කාණ්ඩ ගණන, ඒ සෑම එකක්ම සම්මත නිෂ්පාදන 4 කට සමාන වේ - කාණ්ඩ 50 ක් සත්‍යාපනයට යටත් නම්. විසඳුමක්. අහඹු ලෙස තෝරාගත් සෑම කොටසකම සම්මත අයිතම 4ක් තිබීමේ සම්භාවිතාව නියතය; යන්නෙන් දක්වමු ρ
.එවිට සසම්භාවී විචල්‍යයේ ගණිතමය අපේක්ෂාව xසමාන එම්(x)=
50∙ρ.
අපි සම්භාවිතාව සොයා බලමු ρ
බර්නූලි සූත්‍රයට අනුව: ρ=පී 5 (4)= එම්(x)=
50∙0,32=16. 4.8
. දාදු කැට තුනක් දමනවා. පහත වැටුණු ලක්ෂ්‍යවල එකතුවේ ගණිතමය අපේක්ෂාව සොයන්න. විසඳුමක්.අහඹු විචල්‍යයක ව්යාප්තිය ඔබට සොයාගත හැකිය x- පහත වැටුණු ලක්ෂ්‍යවල එකතුව සහ පසුව එහි ගණිතමය අපේක්ෂාව. කෙසේ වෙතත්, මෙම මාර්ගය ඉතා අපහසුයි. අහඹු විචල්‍යයක් නියෝජනය කරමින් වෙනත් උපක්‍රමයක් භාවිතා කිරීම පහසුය x, එහි ගණිතමය අපේක්ෂාව ගණනය කළ යුත්තේ, සරල අහඹු විචල්‍ය කිහිපයක එකතුවක් ලෙස, ගණනය කිරීමට පහසු වන ගණිතමය අපේක්ෂාවයි. අහඹු විචල්යය නම් x මමලබා ගත් ලකුණු ගණන වේ මම-වන අස්ථි ( මම= 1, 2, 3), පසුව ලකුණු එකතුව xස්වරූපයෙන් ප්රකාශිත X = X 1 + X 2 + X 3 . මුල් අහඹු විචල්‍යයේ ගණිතමය අපේක්ෂාව ගණනය කිරීම සඳහා, එය ඉතිරිව ඇත්තේ ගණිතමය අපේක්ෂාවේ ගුණය භාවිතා කිරීමට පමණි. එම්(x 1
+ X 2 + X 3
)= එම්(x 1
)+ එම්(x 2)+ එම්(x 3
). ඒක පැහැදිලියි ආර්(x මම = කේ)=
1/6, වෙත=
1, 2, 3, 4, 5, 6,
මම=
1,
2, 3. එබැවින් අහඹු විචල්‍යයක ගණිතමය අපේක්ෂාව x මමආකෘතිය ඇත එම්(x මම)
=
1/6∙1
+ 1/6∙2
+1/6∙3
+ 1/6∙4
+ 1/6∙5
+ 1/6∙6
= 7/2, එම්(x)
=
3∙7/2 = 10,5.
4.9.
පරීක්ෂණය අතරතුර අසමත් වූ උපාංග සංඛ්‍යාවේ ගණිතමය අපේක්ෂාව තීරණය කරන්න, නම්: අ) සියලුම උපාංග සඳහා අසාර්ථක වීමේ සම්භාවිතාව සමාන වේ ආර්, සහ පරීක්ෂණයට ලක්වන උපාංග ගණන සමාන වේ n; ආ) අසාර්ථක වීමේ සම්භාවිතාව මම
–
උපකරණයට සමාන වේ පි මම
,
මම=
1,
2, … , n. විසඳුමක්.සසම්භාවී විචල්‍යයට ඉඩ දෙන්න xඅසාර්ථක උපාංග ගණන, එසේ නම් X = X 1 + X 2 +… + X n ,
x මම
=
ඒක පැහැදිලියි ආර්(x මම =
1)=
ආර් මම ,
ආර්(x මම =
0)=
1–
ආර් මම ,i= 1,
2,
…
,n. එම්(x මම)=
1∙ආර් මම +
0∙(1-ආර් මම)=පී මම , එම්(x)= එම්(x 1)+ එම්(x 2)+… +එම්(x n)=පී 1 +P 2 + ... + පී n .
"a" නම්, උපාංගය අසමත් වීමේ සම්භාවිතාව සමාන වේ, i.e. ආර් මම =p,i= 1,
2, …
,n. එම්(x)=
np. අහඹු විචල්යය බව යමෙකු දුටුවහොත් මෙම පිළිතුර වහාම ලබා ගත හැකිය xපරාමිති සහිත ද්විපද ව්‍යාප්තියක් ඇත ( n,
පි).
4.10.
ඩයිස් දෙකක් එකවරම දෙවරක් විසි කරයි. විවික්ත අහඹු විචල්‍යයක් සඳහා ද්විපද ව්‍යාප්ති නියමයක් ලියන්න X -දාදු කැට දෙකක ඉරට්ටේ ලක්ෂ්‍ය සංඛ්‍යාවක සිදුවීම් ගණන. විසඳුමක්. ඉඩ නමුත්=(පළමු මරණයේ ඉරට්ටේ අංකයක් අහිමි වීම), B =(දෙවන මරණයේ ඉරට්ටේ අංකයක් අහිමි වීම). එක් විසිකිරීමකදී දාදු කැට දෙකෙහිම ඉරට්ටේ අංකයක් නැතිවීම නිෂ්පාදනයෙන් ප්‍රකාශ කෙරේ AB.ඉන්පසු ආර්
(AB)
= ආර්(නමුත්)∙ආර්(හිදී)
=
දාදු කැට දෙකේ දෙවන විසි කිරීමේ ප්රතිඵලය පළමුවැන්න මත රඳා නොපවතී, එබැවින් බර්නූලි සූත්රය අදාළ වේ n
=
2,p = 1/4,
q
=
1– පි = 3/4.
අහඹු අගය x 0, 1, 2 අගයන් ගත හැක ,
බර්නූලි සූත්රය මගින් අප සොයා ගන්නා සම්භාවිතාව: ආර්(X= 0)= පී 2
(0)
=
q
2
= 9/16, ආර්(X= 1)= පී 2
(1)= සී ආර්(X= 2)= පී 2
(2)= සී සසම්භාවී විචල්‍ය බෙදා හැරීම් මාලාව X: 4.11.
උපාංගය කාලයත් සමඟ එක් එක් මූලද්රව්යයේ අසාර්ථක වීමේ එකම ඉතා කුඩා සම්භාවිතාවක් සහිත ස්වාධීනව ක්රියාත්මක වන මූලද්රව්ය විශාල සංඛ්යාවක් සමන්විත වේ. ටී. කාලයත් සමඟ අසාර්ථක වීමේ සාමාන්ය සංඛ්යාව සොයා ගන්න ටීමූලද්රව්ය, මෙම කාලය තුළ අවම වශයෙන් එක් මූලද්රව්ය අසමත් වීමේ සම්භාවිතාව 0.98 නම්. විසඳුමක්.
කාලයත් සමඟ අසාර්ථක වීම් ගණන ටීමූලද්රව්ය - අහඹු විචල්යයකි x, Poisson නීතියට අනුව බෙදා හරිනු ලබන, මූලද්රව්ය සංඛ්යාව විශාල බැවින්, මූලද්රව්ය ස්වාධීනව ක්රියා කරන අතර එක් එක් මූලද්රව්යයේ අසාර්ථක වීමේ සම්භාවිතාව කුඩා වේ. සිදුවීමක සාමාන්ය සිදුවීම් සංඛ්යාව nඅත්හදා බැලීම් සමාන වේ එම්(x)
=
np.
අසාර්ථක වීමේ සම්භාවිතාව නිසා වෙතසිට මූලද්රව්ය nසූත්‍රයෙන් ප්‍රකාශ වේ ආර් n
(වෙත)
කොහෙද
=
np, එවිට කිසිදු මූලද්රව්යයක් නියමිත වේලාවට අසමත් වීමේ සම්භාවිතාව ටී
අපි ලබාගන්නවා K = 0: ආර් n
(0)= ඊ - . එබැවින්, ප්රතිවිරුද්ධ සිදුවීමේ සම්භාවිතාව කාලයත් සමග වේ ටී
අවම වශයෙන් එක් මූලද්රව්යයක් අසමත් වේ - 1 ට සමාන වේ - ඊ -
ගැටලුවේ තත්ත්වය අනුව, මෙම සම්භාවිතාව 0.98 ට සමාන වේ. සමීකරණයෙන් 1
- ඊ -
= 0,98, ඊ -
= 1 – 0,98 =
0,02, මෙතැන් සිට
=
-ln
0,02
4. ඒ නිසා කාලය සඳහා ටීඋපාංගයේ ක්රියාකාරිත්වය සාමාන්යයෙන් මූලද්රව්ය 4 කින් අසාර්ථක වනු ඇත. 4.12
. "දෙකක්" රෝල් කරන තුරු ඩයි රෝල් කරනු ලැබේ. සාමාන්ය ටෝස් ගණන සොයන්න. විසඳුමක්. අපි සසම්භාවී විචල්‍යයක් හඳුන්වා දෙමු x- අපට උනන්දුවක් දක්වන සිදුවීම සිදු වන තෙක් සිදු කළ යුතු පරීක්ෂණ ගණන. සම්භාවිතාව x= 1 යනු ඩයි එකේ එක විසි කිරීමකදී "දෙකක්" වැටෙන සම්භාවිතාවට සමාන වේ, i.e. ආර්(X= 1)
= 1/6. සිදුවීම x= 2 යනු පළමු අත්හදා බැලීමේදී "දෙක" වැටුණේ නැත, නමුත් දෙවන එකේදී එය වැටුණි. සිදුවීම් සම්භාවිතාව x= 2 ස්වාධීන සිදුවීම්වල සම්භාවිතාව ගුණ කිරීමේ රීතිය මගින් අපි සොයා ගනිමු: ආර්(X= 2)
= (5/6)∙(1/6) එලෙසම, ආර්(X= 3)
= (5/6) 2 ∙1/6, ආර්(X= 4)
= (5/6) 2 ∙1/6 ආදිය අපට සම්භාවිතා බෙදා හැරීම් මාලාවක් ලැබේ: (5/6) වෙත
∙1/6 සාමාන්ය විසිකිරීම් ගණන (අත්හදා බැලීම්) ගණිතමය අපේක්ෂාවයි එම්(x)
=
1∙1/6 +
2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6
+ … + වෙත
(5/6) වෙත -1 ∙1/6
+ … = 1/6∙(1+2∙5/6 +3∙(5/6) 2
+ … + වෙත
(5/6) වෙත -1
+ …) අපි මාලාවේ එකතුව සොයා ගනිමු: ප්රතිඵලයක් වශයෙන්, එම්(x)
=
(1/6) (1/ (1 –
5/6) 2
= 6. මේ අනුව, “ඩියුස්” වැටෙන තුරු සාමාන්යයෙන් දාදු කැට 6 ක් විසි කිරීම අවශ්‍ය වේ. 4.13.
සිදුවීම සිදුවීමේ එකම සම්භාවිතාව සමඟ ස්වාධීන පරීක්ෂණ සිදු කරනු ලැබේ නමුත්සෑම පරීක්ෂණයකදීම. සිදුවීමක් සිදුවීමේ සම්භාවිතාව සොයන්න නමුත්ස්වාධීන අත්හදා බැලීම් තුනක සිදුවීමේ සිදුවීම් ගණනෙහි විචලනය 0.63 නම් .
විසඳුමක්.අත්හදා බැලීම් තුනේ සිදුවීමේ සිදුවීම් ගණන අහඹු විචල්යයකි xද්විපද නීතිය අනුව බෙදා හරිනු ලැබේ. ස්වාධීන අත්හදා බැලීම් වලදී සිදුවීමක සිදුවීම් සංඛ්‍යාවේ විචලනය (එක් එක් අත්හදා බැලීමේ සිදුවීමක් සිදුවීමේ එකම සම්භාවිතාව සමඟ) අත්හදා බැලීම් සංඛ්‍යාවේ ගුණිතයට සමාන වන අතර සිදුවීම සිදුවීමේ සහ සිදුනොවීමේ සම්භාවිතාව ( කාර්යය 4.6) ඩී(x)
=
npq.
කොන්දේසිය අනුව n
=
3,
ඩී(x)
=
0.63, ඒ නිසා ඔබට පුළුවන් ආර්සමීකරණයෙන් සොයා ගන්න 0,63
= 3∙ආර්(1-ආර්), විසඳුම් දෙකක් ඇති ආර් 1
=
0.7 සහ ආර් 2
=
0,3.
1.2.
p4=0.1; x≤-1 සඳහා 0,
(Fig.5)
x≤a සඳහා https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0,
,
සාමාන්ය වක්රය x=m සරල රේඛාවට සාපේක්ෂව සමමිතික වේ, උපරිමය x=a ට සමාන වේ.
,
විසඳුමක්.
ආයුධ ලාංඡනයක් නොවැටීමේ සම්භාවිතාව: P(0) = 0.5*0.5*0.5= 0.125
P(1) = 0,5
*0,5*0,5 + 0,5*0,5
*0,5 + 0,5*0,5*0,5
= 3*0,125=0,375
P(2) = 0,5
*0,5
*0,5 + 0,5
*0,5*0,5
+ 0,5*0,5
*0,5
= 3*0,125=0,375
කබා තුනක් වැටීමේ සම්භාවිතාව: P(3) = 0.5 * 0.5 * 0.5 = 0.125
පරීක්ෂා කරන්න: P = P (0) + P (1) + P (2) + P (3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 x 0
1
2
3
පී 0,125
0,375
0,375
0,125
විසඳුමක්.
A සිදුවීම සලකා බලන්න - ඉලක්කයට එක් පහරක්. මෙම සිදුවීමේ සිදුවිය හැකි සිදුවීම් පහත පරිදි වේ:
එවිට A සිදුවීමේ සම්භාවිතාව - ඉලක්කයට හරියටම එක් පහරක්, සමාන වනු ඇත: P(A) = 0.12+0.17+0.68 = 0.97 
, අහඹු විචල්යය එක් එක් අගයන් ගන්නා, i.e. 
.අර්ථය
...
සම්භාවිතාව
...
නොගැලපෙන සහ හැකි එකම ඒවා වේ: ඒවා සම්පූර්ණ සිදුවීම් පද්ධතියක් සාදයි. එබැවින්, ඒවායේ සම්භාවිතා එකතුව එකකට සමාන වේ:
.ජයග්රාහී මුදල -100
900
2900
සම්භාවිතාව 0,94
0,04
0,02
විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ කාර්යය: ඉදිකිරීම්
, අහඹු විචල්‍යයේ අගය සම්භාවිතාව තීරණය කරයි xසීමිත අගයට වඩා අඩු හෝ සමාන වේ x.අර්ථය 1
2
3
4
5
6
සම්භාවිතාව 1/6
1/6
1/6
1/6
1/6
1/6
අර්ථය 0
1
2
3
සම්භාවිතාව 1/30
3/10
1/2
1/6
. හිදී
විවික්ත අහඹු විචල්‍යයක බෙදා හැරීමේ කාර්යය: ගණනය කිරීම
විවාහයේ දිග (වසර) අංකය සම්භාවිතාව එෆ්(x)
0
10
0,002
0,002
1
80
0,013
0,015
2
177
0,029
0,044
3
209
0,035
0,079
4
307
0,051
0,130
5
335
0,056
0,186
6
358
0,060
0,246
7
413
0,069
0,314
8
432
0,072
0,386
9
402
0,067
0,453
10 හෝ ඊට වැඩි 3287
0,547
1,000
සමස්ත 6010
1
විවික්ත අහඹු විචල්‍යයක ව්‍යාප්ති නියමය සහ ගණිතමය අපේක්ෂාව සහ විචලනය අතර සම්බන්ධය
(1)
, (2)
.
,
උපග්රන්ථය
සංයෝජනවල මූලද්රව්ය
සිදුවීම් මත ක්රියා
;
;
සම්භාවිතාව පිළිබඳ සම්භාව්ය අර්ථ දැක්වීම
, සිදුවීම සිදුවීමට හිතකරය නමුත්, මුළු අත්හදා බැලීම් ගණනට 
:
සම්භාවිතා ගුණ කිරීමේ සූත්රය
සූත්රය භාවිතයෙන් සොයා ගත හැක:
- සිදුවීම් සම්භාවිතාව නමුත්,
- සිදුවීම් සම්භාවිතාව හිදී,
- සිදුවීම් සම්භාවිතාව හිදීසිද්ධිය බව සපයා ඇත නමුත්දැනටමත් සිදුවී ඇත.
සම්භාවිතා එකතු කිරීමේ සූත්රය
සූත්රය භාවිතයෙන් සොයා ගත හැක:
- සිදුවීම් ඒකාබද්ධ සිදුවීමේ සම්භාවිතාව නමුත්හා හිදී.
සම්පූර්ණ සම්භාවිතා සූත්රය
,
,
…,
අපි ඒවාට උපකල්පන කියමු. ද දනී 
- ඉටු වීමේ සම්භාවිතාව මම-වන කල්පිතය සහ 
- ක්රියාත්මක කිරීමේදී A සිදුවීමේ සම්භාවිතාව මම th කල්පිතය. එවිට සිදුවීමේ සම්භාවිතාව නමුත්සූත්රය භාවිතයෙන් සොයා ගත හැක:
බර්නූලි යෝජනා ක්රමය
බර්නූලි යෝජනා ක්‍රමයේ, මෙය ඉහළම සම්භාවිතාවට අනුරූප වන යම් සිදුවීමක සිදුවීම් ගණනයි. සූත්රය භාවිතයෙන් සොයා ගත හැක:
අහඹු විචල්යයන්
විවික්ත අහඹු විචල්‍යවල සංඛ්යාත්මක ලක්ෂණ
x
ආර්
බෙදා හැරීමේ කාර්යය
විභාගය සඳහා ප්රශ්න
.
.
,
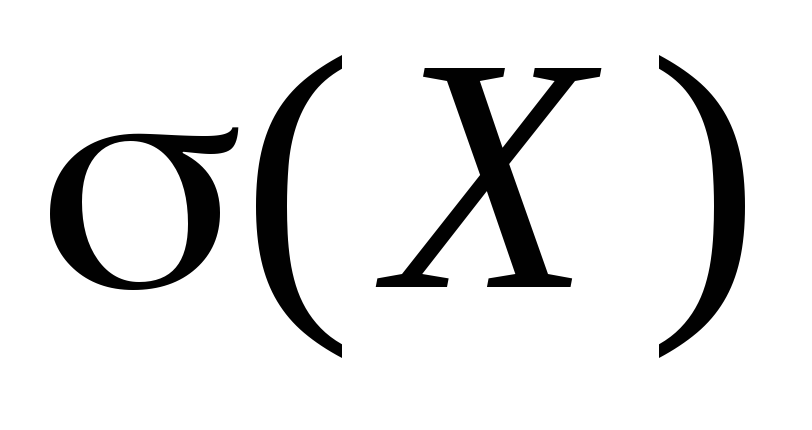0,3(0,7) 2
= 0,441,
(0,3) 2 0,7
= 0,189,
.
.
.
,
,ආර් 2 (1)
=
∙
,ආර් 2 (2)
=
=1/5,
= 3/5,
= 1/5.
ρ
වෙත
(1-ρ
) n-වෙත
ρq n- 1
ρq n- 2
ρ
n
ρq n -
1
+2
ρ
2
q n -
2
+…+.n
ρ
n
= 0,94∙0,1=0,32.
.
,ආර්∙q
=
6/16,
,
ආර් 2
=
1/16.
,
වෙතg
වෙත -1
= (
g වෙත)
g
.
