Закон розподілу випадкової величини знайти математичне очікування. Дискретні випадкові величини. закон розподілу дискретної випадкової величини
Розділ 1. Дискретна випадкова величина
§ 1. Поняття випадкової величини.
Закон розподілу дискретної випадкової величини.
Визначення : Випадковою називається величина, яка в результаті випробування приймає тільки одне значення з можливої безлічі своїх значення, наперед невідоме і залежить від випадкових причин.
Розрізняють два види випадкових величин: дискретні та безперервні.
Визначення : Випадкова величина Х називається дискретний (перервний), якщо безліч її значень кінцеве чи нескінченне, але лічильне.
Іншими словами, можливі значення дискретної випадкової величини можна перенумерувати.
Описати випадкову величину можна з її закону розподілу.
Визначення : Законом розподілу дискретної випадкової величини називають відповідність між можливими значеннями випадкової величини та їх ймовірностями.
Закон розподілу дискретної випадкової величини Х може бути заданий у вигляді таблиці, у першому рядку якої вказані в порядку зростання всі можливі значення випадкової величини, а в другому рядку відповідні ймовірності цих значень, тобто.
де р1 + р2 + ... + рn = 1
Така таблиця називається рядом розподілу дискретної випадкової величини.
Якщо безліч можливих значень випадкової величини нескінченно, ряд р1+ р2+…+ рn+… сходиться та її сума дорівнює 1.
Закон розподілу дискретної випадкової величини Х можна зобразити графічно, для чого прямокутної системикоординат будують ламану, що з'єднує послідовно точки з координатами (xi; pi), i = 1,2, ... n. Отриману лінію називають багатокутником розподілу (Рис.1).
Органічна хімія органічної хімії відповідно дорівнюють 0,7 і 0,8. Скласти закон розподілу випадкової величини Х - числа іспитів, які здасть студент.
Рішення. Розглянута випадкова величина X в результаті іспиту може прийняти одне з наступних значень: x1 = 0, x2 = 1, х3 = 2.
Знайдемо ймовірність цих значень. Позначимо події:
https://pandia.ru/text/78/455/images/image004_81.jpg" width="259" height="66 src=">
 |
Отже, закон розподілу випадкової величини Х визначається таблицею:
Контроль: 0,6 +0,38 +0,56 = 1.
§ 2. Функція розподілу
Повний опис випадкової величини також дає функція розподілу.
Визначення: Функцією розподілу дискретної випадкової величини Х називається функція F(x), що визначає для кожного значення х ймовірність того, що випадкова величина Х прийме значення менше х:
F(x)=Р(Х<х)
Геометрично функція розподілу інтерпретується як ймовірність того, що випадкова величина Х прийме значення, яке зображується на числовій прямій точці, що лежить ліворуч від точки х.
1)0≤ F(x) ≤1;
2) F(x)- незнижена функція на (-∞; + ∞);
3) F(x)- безперервна ліворуч у точках х= xi (i=1,2,…n) і безперервна переважають у всіх інших точках;
4) F(-∞)=Р (Х<-∞)=0 как вероятность невозможного события Х<-∞,
F(+∞)=Р(Х<+∞)=1 как вероятность достоверного события Х<-∞.
Якщо закон розподілу дискретної випадкової величини Х заданий у вигляді таблиці:
то функція розподілу F(x) визначається формулою:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110">
0 при х≤ x1,
р1 при x1< х≤ x2,
F(x)= р1 + р2 при x2< х≤ х3
1 при х>хn.
Її графік зображено на рис.2:

§ 3. Числові характеристики дискретної випадкової величини.
До важливих числових характеристик належить математичне очікування.
Визначення: Математичним очікуванням М(Х) дискретної випадкової величини Х називається сума творів всіх її значень відповідні їм ймовірності:
М(Х) = ∑ xiрі = x1р1 + x2р2+…+ xnрn
Математичне очікування є характеристикою середнього значення випадкової величини.
Властивості математичного очікування:
1) M(C)=C, де З-постійна величина;
2) М (З Х) = З М (Х),
3)М(Х±Y)=М(Х)±M(Y);
4) M (X Y) = M (X) M (Y), де X, Y - незалежні випадкові величини;
5) M(X±C)=M(X)±C, де З-постійна величина;
Для характеристики ступеня розсіювання можливих значень дискретної випадкової величини навколо середнього значення служить дисперсія.
Визначення: Дисперсією D ( X ) випадкової величини Х називається математичне очікування квадрата відхилення випадкової величини від її математичного очікування:
Властивості дисперсії:
1)D(C)=0, де З-постійна величина;
2) D(X)>0, де Х - випадкова величина;
3)D(C X)=C2 D(X), де З-постійна величина;
4) D (X + Y) = D (X) + D (Y), де X, Y - незалежні випадкові величини;
Для обчислення дисперсії часто буває зручно користуватися формулою:
D(X)=M(X2)-(M(X))2,
де М(Х) = ∑ xi2рi = x12р1 + x22р2 + ... + xn2рn
Дисперсія D(X) має розмірність квадрата випадкової величини, що завжди зручно. Тому як показник розсіювання можливих значень випадкової величини використовують також величину D(X).
Визначення: Середнім квадратичним відхиленням σ(Х) випадкової величини Х називається квадратний корінь з дисперсії:
![]()
Завдання №2.Дискретна випадкова величина Х задана законом розподілу:
Знайти Р2, функцію розподілу F(x) та побудувати її графік, а також M(X),D(X), σ(Х).
Рішення: Оскільки сума ймовірностей можливих значень випадкової величини Х дорівнює 1, то
Р2 = 1 - (0,1 +0,3 +0,2 +0,3) = 0,1
Знайдемо функцію розподілу F(х)=P(X Геометрично цю рівність можна витлумачити так: F(х) є ймовірність того, що випадкова величина прийме значення, яке зображується на числовій осі точкою, що лежить ліворуч від точки х. Якщо х≤-1, то F(х)=0, тому що на (-∞;х) немає жодного значення даної випадкової величини; Якщо -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; Якщо 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;х) потрапляють два значення x1=-1 і x2=0; Якщо 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Якщо 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Якщо х>3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)+Р(Х=3)= 0,1 +0,1+0,3+0,2+0,3=1, тому що в проміжок (-∞;х) потрапляють чотири значення x1=-1, x2=0,x3=1,х4=2 та х5=3. https://pandia.ru/text/78/455/images/image006_89.gif" width="14 height=2" height="2"> 0 при х≤-1, 0,1 при -1<х≤0, 0,2 при 0<х≤1, F(x)= 0,5 при 1<х≤2, 0,7 при 2<х≤3, 1 при х>3 Зобразимо функцію F(x)графічно (рис.3): https://pandia.ru/text/78/455/images/image014_24.jpg" width="158 height=29" height="29">≈1,2845. §
4. Біноміальний закон розподілу дискретна випадкова величина, закон Пуассона. Визначення: Біноміальним
називається закон розподілу дискретної випадкової величини Х - числа події А в n незалежних повторних випробуваннях, в кожному з яких події А може наступити з ймовірністю p або не наступити з ймовірністю q=1-p. Тоді Р(Х=m)-імовірність появи події А рівно m разів у n випробуваннях обчислюється за формулою Бернуллі: Р(Х=m)=Сmnpmqn-m Математичне очікування, дисперсію та середнє квадратичне відхиленнявипадкової величини Х, розподіленої за бінарним законом, знаходять відповідно за формулами: https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> Імовірність події А - «випадання п'ятірки» в кожному випробуванні одна і та ж і дорівнює 1/6, тобто . Р(А)=р=1/6, тоді Р(А)=1-p=q=5/6, де - «Випадання не п'ятірки». Випадкова величина Х може набувати значень: 0;1;2;3. Імовірність кожного з можливих значень Х знайдемо за формулою Бернуллі: Р(Х=0)=Р3(0)=С03р0q3=1 (1/6)0 (5/6)3=125/216; Р(Х=1)=Р3(1)=С13р1q2=3 (1/6)1 (5/6)2=75/216; Р(Х=2)=Р3(2)=С23р2q =3 (1/6)2 (5/6)1=15/216; Р(Х=3)=Р3(3)=С33р3q0=1 (1/6)3 (5/6)0=1/216. Т. о. закон розподілу випадкової величини Х має вигляд: Контроль: 125/216+75/216+15/216+1/216=1. Знайдемо числові характеристики випадкової величини Х: M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, Завдання №4.Верстат-автомат штампує деталі. Імовірність того, що виготовлена деталь виявиться бракованою, дорівнює 0,002. Знайти ймовірність того, що серед 1000 відібраних деталей виявиться: а) 5 бракованих; б) хоч би одна бракована. Рішення:
Число n=1000 велике, ймовірність виготовлення бракованої деталі р=0,002 мала, і події, що розглядаються (деталь виявиться бракованою) незалежні, тому має місце формула Пуассона: Рn(m)= e-
λ
λm Знайдемо λ=np=1000 0,002=2. а)Знайдемо ймовірність того, що буде 5 бракованих деталей (m=5): Р1000 (5) = e-2
25
= 32 0,13534
= 0,0361 б)Знайдемо ймовірність того, що буде хоча б одна бракована деталь. Подія А -«хоча одна з відібраних деталей бракована» є протилежною події -«всі відібрані деталі не браковані». Отже, Р(А)=1-Р(). Звідси шукана ймовірність дорівнює: Р(А)=1-Р1000(0)=1- e-2
20
= 1 - e-2 = 1-0,13534 ≈ 0,865. Завдання для самостійної роботи.
1.1
1.2.
Дисперсна випадкова величина Х задана законом розподілу: Знайти р4, функцію розподілу F(X) та побудувати її графік, а також M(X),D(X), σ(Х). 1.3.
У коробці 9 фломастерів, з яких 2 фломастери вже не пишуть. Навмання беруть 3 фломастери. Випадкова величина Х - число друкарських фломастерів серед взятих. Скласти закон розподілу випадкової величини. 1.4.
На стелажі бібліотеки у випадковому порядку розставлено 6 підручників, причому 4 з них у палітурці. Бібліотекар бере навмання 4 підручники. Випадкова величина Х-число підручників у палітурці серед взятих. Скласти закон розподілу випадкової величини. 1.5.
У квитку два завдання. Ймовірність правильного рішенняпершого завдання дорівнює 0,9, другий-0,7. Випадкова величина Х-число правильно вирішених завдань у квитку. Скласти закон розподілу, обчислити математичне очікування та дисперсію цієї випадкової величини, а також знайти функцію розподілу F(x) та побудувати її графік. 1.6.
Три стрілки стріляють по мішені. Імовірність попадання в ціль при одному пострілі для першого стрілка дорівнює 0,5, для другого-0,8, для третього -0,7. Випадкова величина Х - число попадань у ціль, якщо стрілки роблять по одному пострілу. Знайти закон розподілу, M(X), D(X). 1.7.
Баскетболіст кидає м'яч у кошик із ймовірністю влучення при кожному кидку 0,8. За кожне влучення він отримує 10 очок, а у разі промаху очки йому не нараховують. Скласти закон розподілу випадкової величини Х-числа очок, отриманих баскетболістом за 3 кидки. Знайти M(X),D(X), а також можливість того, що він отримає більше 10 очок. 1.8.
На картках написані літери, всього 5 голосних та 3 приголосних. Навмання вибирають 3 картки, причому щоразу взяту картку повертають назад. Випадкова величина Х-число гласних букв серед взятих. Скласти закон розподілу та знайти M(X),D(X),σ(Х). 1.9.
У середньому по 60% договорів страхова компаніявиплачує страхові суми у зв'язку з настанням страхового випадку. Скласти закон розподілу випадкової величини Х - числа договорів, за якими було виплачено страхову суму серед навмання відібраних чотирьох договорів. Знайти числові показники цієї величини. 1.10.
Радіостанція через певні проміжки часу надсилає позивні сигнали (не більше чотирьох) до встановлення двостороннього зв'язку. Імовірність отримання відповіді на позивний сигнал дорівнює 0,3. Випадкова величина Х-число надісланих позивних сигналів. Скласти закон розподілу та знайти F(x). 1.11.
Є 3 ключі, з яких лише один підходить до замку. Скласти закон розподілу випадкової величини Х-числа спроб відкриття замку, якщо випробуваний ключ у наступних спробах не бере участі. Знайти M(X),D(X). 1.12.
Виготовляються послідовні незалежні випробування трьох приладів на надійність. Кожен наступний приладвипробовується лише у тому випадку, якщо попередній виявився надійним. Імовірність витримати випробування для кожного приладу дорівнює 0,9. Скласти закон розподілу випадкової величини Х числа випробуваних приладів. 1.13
.Дискретна випадкова величина Х має три можливі значення: х1 = 1, х2, х3, причому х1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
Блок електронного пристрою має 100 однакових елементів. Імовірність відмови кожного елемента протягом часу Т дорівнює 0,002. Елементи працюють незалежно. Знайти ймовірність те, що за час Т відмовить не більше двох елементів. 1.15.
Підручник видано тиражем 50000 екземплярів. Імовірність того, що підручник зброшурований неправильно, дорівнює 0,0002. Знайти ймовірність того, що тираж містить: а) чотири браковані книги, б) менше двох бракованих книг. 1
.16.
Число дзвінків, що надходять на АТС кожну хвилину, розподілено за законом Пуассона з параметром =1,5. Знайдіть ймовірність того, що за хвилину надійде: а) два виклики; б) хоча б один виклик. 1.17.
Знайти M(Z),D(Z), якщо Z=3X+Y. 1.18.
Наведено закони розподілу двох незалежних випадкових величин: Знайти M(Z),D(Z), якщо Z=X+2Y. Відповіді:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110"> 1.1.
р3 = 0,4; 0 при х≤-2, 0,3 при -2<х≤0, F(x)= 0,5 при 0<х≤2, 0,9 при 2<х≤5, 1 при х>5 0,3 при -1<х≤0, 0,4 при 0<х≤1, F(x)= 0,6 при 1<х≤2, 0,7 при 2<х≤3, 1 при х>3 M(Х)=1; D(Х)=2,6; σ(Х) ≈1,612. https://pandia.ru/text/78/455/images/image025_24.gif" width="2 height=98" height="98"> 0 при х≤0, 0,03 при 0<х≤1, F(x)= 0,37 при 1<х≤2, 1 при х>2 M(Х)=2; D(Х)=0,62 M(Х)=2,4; D(Х)=0,48, P(X>10)=0,896 1.
8
.
M(Х)=15/8; D(Х)=45/64; σ(Х) ≈ M(Х)=2,4; D(Х)=0,96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(Х)=2; D(Х)=2/3 1.14.
1,22 e-0,2 ≈ 0,999 1.15.
а) 0,0189; б) 0,00049 1.16.
а) 0,0702; б) 0,77687 1.17.
3,8; 14,2 1.18.
11,2; 4. Розділ 2. Безперервна випадкова величина
Визначення: Безперервний
називають величину, всі можливі значення якої повністю заповнюють кінцевий чи нескінченний проміжок числової осі. Очевидно, кількість можливих значень безперервної випадкової величини нескінченна. Безперервну випадкову величину можна ставити за допомогою функції розподілу. Визначення:Ф ункцією розподілу
безперервної випадкової величини Х називається функція F(х), що визначає для кожного значення x width="14" Функцію розподілу іноді називають інтегральною функцією розподілу. Властивості функції розподілу:
1)1≤ F(x) ≤1 2)У безперервної випадкової величини функція розподілу безперервна у будь-якій точці і диференційована всюди, крім, можливо, окремих точок. 3) Імовірність потрапляння випадкової величини Х до одного з проміжків (а;b), [а;b), [а;b], дорівнює різниці значень функції F(х) у точках а і b, тобто. Р(а<Х 4) Імовірність того, що безперервна випадкова величина Х набуде одного окремого значення дорівнює 0. 5) F(-∞)=0, F(+∞)=1 Завдання безперервної випадкової величини з допомогою функції розподілу є єдиним. Введемо поняття густини розподілу ймовірностей (щільність розподілу). Визначення
:
Щільністю розподілу ймовірностей
f
(
x
)
безперервної випадкової величини Х називається похідна від її функції розподілу, тобто: Щільність розподілу ймовірностей іноді називають диференціальною функцією розподілу чи диференціальним законом розподілу. Графік щільності розподілу ймовірностей f(x) називається кривою розподілу ймовірностей
.
Властивості густини розподілу ймовірностей:
1)f(x) ≥0,при хhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" height="141">.gif" width="14" height ="62 src="> 0 при х≤2, f(x)= с(х-2) при 2<х≤6, 0 при х>6. Знайти: а) значення с; б) функцію розподілу F(х) та побудувати її графік; в) Р(3≤х<5) Рішення:
+
∞ а) Значення знайдемо з умови нормування: f(x)dx=1. Отже, -∞ https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> -∞ 2 2 х якщо 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х - (4/2-4))= 1/8(х2/2-2х+2)=1/16(х-2)2; Gif" width="14" height="62"> 0 при х≤2, F(х)= (х-2)2/16 при 2<х≤6, 1 при х>6. Графік функції F(х) зображено на рис.3 https://pandia.ru/text/78/455/images/image034_23.gif" width="14" height="62 src="> 0 при х≤0, F(х)= (3 arctg х)/π при 0<х≤√3, 1 при х>√3. Знайти диференціальну функцію розподілу f(х) Рішення:
Т. к.f(х) = F'(x), то https://pandia.ru/text/78/455/images/image011_36.jpg" width="118" height="24"> Усі властивості математичного очікування і дисперсії, розглянуті раніше дисперсних випадкових величин, справедливі й у безперервних. Завдання №3.Випадкова величина Х задана диференціальною функцією f(x): https://pandia.ru/text/78/455/images/image036_19.gif" height="38"> -∞ 2 X3/9 + х2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> +∞ D(X)= ∫ х2 f(x)dx-(М(х))2=∫ х2 х/3 dx+∫1/3х2 dx=(31/18)2=х4/12 +х3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. Завдання для самостійного вирішення.
2.1.
Безперервна випадкова величина Х задана функцією розподілу: 0 при х≤0, F(х)= 0 при х≤ π/6, 0 при х≤ π/6, F(х)= - cos 3x при π/6<х≤ π/3, 1 при х> π/3. Знайти диференціальну функцію розподілу f(x), а також Р(2π /9<Х< π /2). 2.3.
0 при х≤2, f(х)= з х при 2<х≤4, 0 при х>4. 2.4.
Безперервна випадкова величина Х задана щільністю розподілу: 0 при х≤0, f(х)= з √х при 0<х≤1, 0 при х>1. Знайти: а) число с; б) М(Х), D(X). 2.5.
https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" height="39"> при х, 0 при х. Знайти: а) F(х) та побудувати її графік; б) M(X), D(X), σ(Х); в) ймовірність того, що у чотирьох незалежних випробуванняхвеличина Х прийме рівно 2 рази значення, що належить інтервалу (1; 4). 2.6.
Задано щільність розподілу ймовірностей безперервної випадкової величини Х: f(х)= 2(х-2) при х, 0 при х. Знайти: а) F(х) та побудувати її графік; б) M(X), D(X), σ(Х); в) ймовірність того, що у трьох незалежних випробуваннях величина Х прийме рівно 2 рази значення, що належить відрізку . 2.7.
Функція f(х) задана у вигляді: https://pandia.ru/text/78/455/images/image045_4.jpg" width="43" height="38 src=">.jpg" width="16" height="15">[-√ 3/2; √3/2]. 2.8.
Функція f(x) задана у вигляді: https://pandia.ru/text/78/455/images/image046_5.jpg" width="45" height="36 src="> .jpg" width="16" height="15">[- π /4; π /4]. Знайти: а) значення постійної с, коли він функція буде щільністю ймовірності деякої випадкової величини Х; б) функцію розподілу F(x). 2.9.
Випадкова величина Х, зосереджена інтервалі (3;7), задана функцією розподілу F(х)= . Знайти ймовірність того, що випадкова величина Х набуде значення: а) менше 5; б) не менше 7. 2.10.
Випадкова величина Х, зосереджена на інтервалі (-1; 4), задана функцією розподілу F(х) = . Знайти ймовірність того, що випадкова величина Х набуде значення: а) менше 2; б) не менше 4. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" height="44 src="> .jpg" width="16" height="15">. Знайти: а) число с; б) М(Х); в) ймовірність Р(Х> М(Х)). 2.12.
Випадкова величина задана диференціальною функцією розподілу: https://pandia.ru/text/78/455/images/image050_3.jpg" width="60" height="38 src=">.jpg" width="16 height=15" height="15"> . Знайти: а) М(Х); б) ймовірність Р(Х≤М(Х)) 2.13.
Розподіл Рем'я задається щільністю ймовірності: https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" height="37"> при х ≥0. Довести, що f(x) дійсно є густиною розподілу ймовірностей. 2.14.
Задано щільність розподілу ймовірностей безперервної випадкової величини Х: https://pandia.ru/text/78/455/images/image054_3.jpg" width="174" height="136 src=">(рис.4) 2.16.
Випадкова величина Х розподілена згідно із законом « прямокутного трикутника»в інтервалі (0; 4) (рис.5). Знайти аналітичний вираз для густини ймовірності f(x) на всій числовій осі. Відповіді
0 при х≤0, f(х)= 0 при х≤ π/6, 0 при х≤ π/6, F(х)= 3sin 3x при π/6<х≤ π/3, 0 при х> π/3. Безперервна випадкова величина Х має рівномірний законрозподілу на деякому інтервалі (а;b), якому належать всі можливі значення Х, якщо щільність розподілу ймовірностей f(x) постійна цьому інтервалі і дорівнює 0 поза ним, тобто. 0 при х≤а, f(х)= при a<х 0 при х≥b. Графік функції f(x) зображено на рис. 1 F(х) = width="30", D(X)=, σ(Х)=. Завдання №1.Випадкова величина Х рівномірно розподілена на відрізку. Знайти: а) щільність розподілу ймовірностей f(x) та побудувати її графік; б) функцію розподілу F(x) та побудувати її графік; в) M(X), D(X), σ(Х). Рішення:
Скориставшись формулами, розглянутими вище, а=3, b=7, знаходимо: https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" height="39"> при 3≤х≤7, 0 при х>7 Побудуємо її графік (рис.3): https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86 src="> 0 при х≤3, F(х)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" height="119 src=">рис.4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" height="43">==https://pandia.ru/text/ 78/455/images/image092_10.gif" width="14" height="49 src="> 0 при х<0, f(х)= λе-λх при х≥0. Функція розподілу випадкової величини Х, розподіленої за показовим законом, задається формулою: https://pandia.ru/text/78/455/images/image094_4.jpg" width="191" height="126 src=">рис..jpg" width="22" height="30"> , D(X)=, σ(Х)= Таким чином, математичне очікування та середнє квадратичне відхилення показового розподілу рівні між собою. Імовірність потрапляння Х до інтервалу (a;b) обчислюється за формулою: Р(a<Х Завдання №2.Середній час безвідмовної роботи приладу дорівнює 100 год. Вважаючи, що час безвідмовної роботи приладу має показовий закон розподілу, знайти: а) густина розподілу ймовірностей; б) функцію розподілу; в) ймовірність, що час безвідмовної роботи приладу перевищить 120 год. Рішення:
За умовою математичний розподіл M(X) = 0 при х<0, а) f(х)= 0,01-0,01х при х≥0. б) F(x)= 0 при х<0, 1-е -0,01х при х≥0. в) Шукану ймовірність знайдемо, використовуючи функцію розподілу: Р(X>120)=1-F(120)=1-(1- е -1,2)= е -1,2 ≈0,3. §
3.Нормальний закон розподілу Визначення:
Безперервна випадкова величина Х має нормальний закон розподілу (закон Гауса),
якщо її щільність розподілу має вигляд: де m=M(X), σ2=D(X), σ>0. Криву нормального закону розподілу називають нормальної або гаусової кривої
(Мал.7) Функція розподілу випадкової величини Х, розподіленої за нормальним законом, виражається через функцію Лапласа Ф(х) за формулою: де – функція Лапласа. Примітка:
Функція Ф(х) є непарною (Ф(-х)=-Ф(х)), крім того, при х>5 вважатимуться Ф(х) ≈1/2. Графік функції розподілу F(x) зображено на рис. 8 https://pandia.ru/text/78/455/images/image106_4.jpg" width="218" height="33"> Імовірність того, що абсолютна величинавідхилення менше позитивного числаδ обчислюється за формулою: Зокрема, при m=0 справедлива рівність: «Правило трьох сигм»
Якщо випадкова величина Х має нормальний закон розподілу з параметрами m і σ то практично достовірно, що її значення укладені в інтервалі (a-3σ; a+3σ), т. до. https://pandia.ru/text/78/455/images/image110_2.jpg" width="157" height="57 src=">а) б) Скористаємося формулою: https://pandia.ru/text/78/455/images/image112_2.jpg" width="369" height="38 src="> По таблиці значень функції Ф(х) знаходимо Ф(1,5)=0,4332, Ф(1)=0,3413. Отже, шукана ймовірність: P(28) Завдання для самостійної роботи
3.1.
Випадкова величина Х рівномірно розподілена в інтервалі (-3; 5). Знайдіть: б) функції розподілу F(x); в) числові показники; г) ймовірність Р(4<х<6). 3.2.
Випадкова величина Х рівномірно розподілена на відрізку. Знайдіть: а) густина розподілу f(x); б) функції розподілу F(x); в) числові показники; г) ймовірність Р(3?х?6). 3.3.
На шосе встановлено автоматичний світлофор, в якому 2 хвилини для транспорту горить зелене світло, 3 секунди жовте і 30 секунд червоне і т. д. Машина проїжджає шосе у випадковий момент часу. Знайти ймовірність того, що машина проїде повз світлофор, не зупиняючись. 3.4.
Поїзди метрополітену йдуть регулярно з інтервалом 2 хвилини. Пасажир виходить на платформу у довільний момент часу. Яка ймовірність того, що чекати на поїзд пасажиру доведеться більше 50 секунд. Знайти математичне очікування випадкової величини Х – час очікування поїзда. 3.5.
Знайти дисперсію та середнє квадратичне відхилення показового розподілу, заданого функцією розподілу: F(x)= 0 при х<0, 1-е-8х при х≥0. 3.6.
Безперервна випадкова величина Х задана щільністю розподілу ймовірностей: f(x)= 0 при х<0, 0,7 е-0,7х при х≥0. а) Назвіть закон розподілу випадкової величини, що розглядається. б) Знайдіть функцію розподілу F(X) та числові характеристики випадкової величини Х. 3.7.
Випадкова величина Х розподілена за показовим законом, заданим щільністю розподілу ймовірностей: f(x)= 0 при х<0, 0,4 е-0,4 х при х≥0. Знайти ймовірність того, що в результаті випробування Х набуде значення інтервалу (2,5;5). 3.8.
Безперервна випадкова величина Х розподілена за показовим законом, заданим функцією розподілу: F(x)= 0 при х<0, 1-е-0,6х при х≥0 Знайти ймовірність того, що в результаті випробування Х набуде значення відрізка . 3.9.
Математичне очікування та середнє квадратичне відхилення нормально розподіленої випадкової величини відповідно дорівнюють 8 і 2. Знайдіть: а) густина розподілу f(x); б) ймовірність того, що в результаті випробування Х набуде значення з інтервалу (10; 14). 3.10.
Випадкова величина Х розподілена нормально з математичним очікуванням 3,5 та дисперсією 0,04. Знайдіть: а) густина розподілу f(x); б) ймовірність того, що в результаті випробування Х набуде значення відрізка . 3.11.
Випадкова величина Х розподілена нормально з M(X)=0 та D(X)=1. Яка з подій: |Х|≤0,6 або |Х|≥0,6 має більшу ймовірність? 3.12.
Випадкова величина Х розподілена нормально з M(X)=0 і D(X)=1.З якого інтервалу (-0,5;-0,1) або (1;2) при одному випробуванні вона набуде значення з більшою ймовірністю? 3.13.
Поточна ціна за одну акцію може бути змодельована за допомогою нормального закону розподілу з M(X)=10ден. од. і σ (Х) = 0,3 ден. од. Знайти: а) ймовірність того, що поточна ціна акції буде від 9,8 грош. од. до 10,4 грош. од.; б) за допомогою «правила трьох сигм» знайти межі, в яких буде перебувати поточна ціна акції. 3.14.
Здійснюється зважування речовини без систематичних помилок. Випадкові помилки зважування підпорядковані нормальному закону із середнім квадратичним ставленням σ=5г. Знайти ймовірність того, що в чотирьох незалежних дослідах помилка при трьох зважування не відбудеться за абсолютною величиною 3г. 3.15.
Випадкова величина Х розподілена нормально з M(X)=12,6. Імовірність потрапляння випадкової величини до інтервалу (11,4;13,8) дорівнює 0,6826. Знайдіть середнє квадратичне відхилення σ. 3.16.
Випадкова величина Х розподілена нормально з M(X)=12 і D(X)=36. Знайти інтервал, який з ймовірністю 0,9973 потрапить в результаті випробування випадкова величина Х. 3.17.
Деталь, виготовлена автоматично, вважається бракованою, якщо відхилення Х контрольованого параметра від номіналу перевищує по модулю 2 одиниці вимірювання . Передбачається, що випадкова величина Х розподілена нормально з M(X)=0 та σ(Х)=0,7. Скільки відсотків бракованих деталей видає автомат? 3.18.
Параметр Х деталі розподілено нормально з математичним очікуванням 2 рівним номіналу і середнім квадратичним відхиленням 0,014. Знайти ймовірність, що відхилення Х від номіналу по модулю не перевищить 1% номіналу. Відповіді
https://pandia.ru/text/78/455/images/image116_9.gif" width="14" height="110 src="> б) 0 при х≤-3, F(х) = left"> 3.10.
а) f (x) = , б) Р(3,1≤Х≤3,7) ≈0,8185. 3.11.
|x|≥0,6. 3.12.
(-0,5;-0,1). 3.13.
а) Р(9,8≤Х≤10,4) ≈0,6562. 3.14.
0,111. 3.15.
σ=1,2. 3.16.
(-6;30). 3.17.
0,4%. Закон розподілу випадкової величини X: Приклад №2. Ймовірність влучення в мету одного стрільця за одного пострілу першого стрілка дорівнює 0.8, другого стрілка – 0.85. Стрілки зробили по одному пострілу в ціль. Вважаючи попадання в ціль для окремих стрільців подіями незалежними, знайти ймовірність події А – одно попадання в ціль. Випадковою величиною
називається змінна, яка може набувати тих чи інших значень в залежності від різних обставин, і в свою чергу, випадкова величина називається дискретний
, якщо безліч її значень звісно чи счётно. Крім дискретних випадкових величин, існують також безперервні випадкові величини. Розглянемо докладніше поняття випадкової величини. На практиці часто зустрічаються величини, які можуть набувати деяких значень, але не можна достовірно передбачити, яке саме значення кожна з них прийме в досвіді, явищі, спостереженні, що розглядається. Наприклад, кількість хлопчиків, які народяться в Москві найближчого дня, може бути різною. Воно може бути рівним нулю (не народиться жодного хлопчика: народяться всі дівчатка або взагалі не буде новонароджених), одному, двом і так далі до деякого кінцевого числа n. До подібних величин належать: маса коренеплоду цукрових буряків на ділянці, дальність польоту артилерійського снаряда, кількість бракованих деталей у партії тощо. Такі величини називатимемо випадковими. Вони характеризують усі можливі результати досвіду чи спостереження з кількісного боку. Прикладами дискретних випадкових величин
з кінцевим числом значень можуть служити кількість дітей, що народилися, протягом дня в населеному пункті, кількість пасажирів автобуса, кількість пасажирів, перевезених московським метро за добу і т.п. Число значень дискретної випадкової величини може бути і нескінченним, але лічильним безліччю. Але в будь-якому випадку їх можна в якомусь порядку пронумерувати, або, точніше, встановити взаємно-однозначну відповідність між значеннями випадкової величини та натуральними числами 1, 2, 3, ..., n. Увага: нове, дуже важливе поняття теорії ймовірностей закон розподілу
. Нехай Xможе приймати nзначень: . Вважатимемо, що вони всі різні (інакше однакові повинні бути об'єднані) і розташовані в порядку, що зростає. Для повної характеристики дискретної випадкової величини мають бути задані як її значення, а й ймовірності
Законом розподілу дискретної випадкової величини
називається будь-яке правило (функція, таблиця) p(x), що дозволяє знаходити ймовірності всіляких подій, пов'язаних із випадковою величиною (наприклад, ймовірність того, що вона приклад якесь значення або потрапить до якогось інтервалу). Найбільш просто та зручно закон розподілу дискретної випадкової величини задавати у вигляді наступної таблиці: Така таблиця називається поряд розподілу дискретної випадкової величини. У верхньому рядку ряду розподілу перераховані у порядку зростання всі можливі значення дискретної випадкової величини (ікси), а в нижній - ймовірності цих значень ( p). Події приклад 1.У студентській групі організовано лотерею. Розігрується дві речі вартістю по 1000 руб. та одна вартістю по 3000 руб. Скласти закон розподілу суми чистого виграшу для студента, який придбав один квиток за 100 руб. Усього продано 50 квитків. Рішення. Випадкова величина, що цікавить нас Xможе приймати три значення: - 100 руб. (якщо студент не виграє, а фактично програє 100 руб., Сплачені ним за квиток), 900 руб. та 2900 руб. (Фактичний виграш зменшується на 100 руб. - На вартість квитка). Першому результату сприяють 47 випадків із 50, другому - 2, а третьому - один. Тому їхні ймовірності такі: P(X=-100)=47/50=0,94
,
P(X=900)=2/50=0,04
,
P(X=2900)=1/50=0,02
. Закон розподілу дискретної випадкової величини Xмає вигляд Ряд розподілу може бути побудований тільки для дискретної випадкової величини (для недискретної він не може бути побудований хоча б тому, що безліч можливих значень такої випадкової величини нечисленна, їх не можна перерахувати у верхньому рядку таблиці). Найбільш загальною формою закону розподілу, придатною всім випадкових величин (як дискретних, і недискретних), є функція розподілу. Функцією розподілу дискретної випадкової величиниабо інтегральною функцієюназивається функція Функція розподілу будь-якої дискретної випадкової величини є розривна ступінчаста функція, стрибки якої відбуваються в точках, що відповідають можливим значенням випадкової величини, і дорівнюють ймовірності цих значень. приклад 2.Дискретна випадкова величина X- Число очок, що випали при киданні гральної кістки. Постояти її функцію розподілу. Рішення. Ряд розподілу дискретної випадкової величини Xмає вигляд: Функція розподілу F(x) має 6 стрибків, рівних за величиною 1/6 (на малюнку внизу). приклад 3.В урні 6 білих куль і 4 чорні кулі. З урни виймають 3 кулі. Число білих куль серед вийнятих куль - дискретна випадкова величина X. Скласти відповідний їй закон розподілу. Xможе приймати значення 0, 1, 2, 3. Відповідні їм ймовірності найпростіше обчислити правилу множення ймовірностей. Отримуємо наступний закон розподілу дискретної випадкової величини: приклад 4.Скласти закон розподілу дискретної випадкової величини - числа попадань у ціль при чотирьох пострілах, якщо ймовірність влучення при одному пострілі дорівнює 0,1. Рішення. Дискретна випадкова величина Xможе приймати п'ять різних значень: 1, 2, 3, 4, 5. Відповідні їм ймовірності знайдемо за формулі Бернуллі
n = 4
, p = 1,1
, q = 1 - p = 0,9
, m = 0, 1, 2, 3, 4
отримуємо Отже, закон розподілу дискретної випадкової величини Xмає вигляд Якщо ймовірність значень дискретної випадкової величини можна визначити за формулою Бернуллі, то випадкова величина має біномний розподіл . Якщо кількість випробувань досить велика, то ймовірність того, що в цих випробуваннях подія, що цікавить, настане саме mраз, підпорядковується закону розподілу Пуассона . Щоб обчислити функцію розподілу дискретної випадкової величини F(х), потрібно скласти ймовірності всіх тих значень, які менші або рівні граничному значенню х. Приклад 5.У таблиці дані залежності кількості розірваних протягом року шлюбів від тривалості шлюбу. Знайти ймовірність того, що черговий розірваний шлюб мав тривалість меншу, ніж 5 років. Рішення. Імовірності обчислені шляхом розподілу числа відповідних розірваних шлюбів на загальне число 6010. Ймовірність того, що черговий розірваний шлюб був тривалістю 5 років, дорівнює 0,056. Імовірність, що тривалість чергового розірваного шлюбу менша чи дорівнює 5 років, дорівнює 0,186. Ми отримали її, додавши до значення F(x) для шлюбів із тривалістю по 4 роки включно ймовірність для шлюбів із тривалістю у 5 років. Часто не всі значення дискретної випадкової величини відомі, але відомі деякі значення або ймовірності з ряду, а також математичне очікування та (або) дисперсія випадкової величини, яким присвячено окремий урок. Наведемо тут деякі формули з цього уроку, які можуть допомогти при складанні закону розподілу дискретної випадкової величини і розберемо приклади вирішення таких завдань. Математичне очікування дискретної випадкової величини - сума творів всіх можливих значень на ймовірності цих значень: Формула дсперсії дискретної випадкової величини за визначенням: Часто для обчислень зручніша наступна формула дисперсії: де Приклад 6.Дискретна випадкова величина Xможе набувати лише два значення. Найменше значення вона набуває з ймовірністю p= 0,6. Знайти закон розподілу дискретної випадкової величини X, якщо відомо, що її математичне очікування та дисперсія. Рішення. Імовірність того, що випадкова величина набуде більшого значення x2
, що дорівнює 1 − 0,6 = 4 . Використовуючи формулу (1) математичного очікування, складемо рівняння, в якому невідомі значення нашої дискретної випадкової величини: Використовуючи формулу (2) дисперсії, складемо інше рівняння, в якому невідомі - значення дискретної випадкової величини: Систему із двох отриманих рівнянь вирішуємо шляхом підстановки. З першого рівняння отримуємо Підставивши цей вираз у друге рівняння, після нескладних перетворень отримаємо квадратне рівняння яке має два корені: 7/5 та −1 . Перший корінь не відповідає умовам завдання, оскільки x2
< x 1
. Таким чином, значення, які може набувати дискретна випадкова величина Xза умовами нашого прикладу, рівні x1
= −1
і x2
= 2
. Дано ряд розподілу дискретної випадкової величини. Знайти ймовірність і побудувати графік функції розподілу. Обчислити математичне очікування та дисперсію цієї величини. Випадкова величина Х набирає лише чотири значення: -4, -3, 1 і 2. Кожне з цих значень вона приймає з певною ймовірністю. Так як сума всіх ймовірностей повинна дорівнювати 1, то недостатня ймовірність дорівнює: 0,3 + ? + 0,1 + 0,4 = 1, Складемо функцію розподілу випадкової величини Х. Відомо, що функція розподілу , тоді: Отже, Побудуємо графік функції F(x)
. Математичне очікування дискретної випадкової величини дорівнює сумі творів значення випадкової величини відповідну ймовірність, тобто. Дисперсію дискретної випадкової величини знайдемо за формулою: Тут: - Факторіал числа Подія – це будь-який факт, який може статися чи не статися внаслідок досвіду. Об'єднання подій Аі У– це подія З, яка полягає у появі або події А, або події У, або обох подій одночасно. Позначення: Перетин подій Аі У– це подія З, що полягає у одночасному появі обох подій. Позначення: Ймовірність події А- Це відношення числа дослідів Ймовірність події Якщо події А та В – незалежні (поява одного не впливає на появу іншого), то ймовірність події дорівнює: Ймовірність події Ймовірність події А, Ймовірність події В, Якщо події А і В несумісні (не можуть з'явитися одночасно), то ймовірність події дорівнює: Нехай подія Аможе статися одночасно з однією з подій Нехай проводиться n незалежних випробувань. Ймовірність появи (успіху) події Ау кожному їх постійна і дорівнює p, ймовірність невдачі (тобто не появи події А) q
=
1 - p. Тоді ймовірність появи kуспіхів у nвипробуваннях можна знайти за формулою Бернуллі: Найімовірніше число успіхів дискретні безперервні (н-р, кількість дівчаток у сім'ї з 5 дітьми) (н-р, час справної роботи чайника) Нехай дискретна величина задана поряд розподілу: , , …, - значення випадкової величини Х; , , …, - відповідні їм значення ймовірностей. Функцією розподілу випадкової величини Хназивається функція , задана на всій числовій прямій і дорівнює ймовірності того, що Хбуде менше х: Подія. Операції над випадковими подіями. Концепція ймовірності події. Правила складання та множення ймовірностей. Умовні можливості. Формула цілковитої ймовірності. Формула Байєса. Схема Бернуллі. Випадкова величина, її функція розподілу та ряд розподілу. Основні характеристики функції розподілу. Математичне очікування. Властивості математичного очікування. Дисперсія. Властивості дисперсії. Щільність розподілу ймовірностей одновимірної випадкової величини. Види розподілів: рівномірний, експоненціальний, нормальний, біноміальний та розподіл Пуассона. Локальна та інтегральні теореми Муавра-Лапласа. Закон та функція розподілу системи двох випадкових величин. Щільність розподілу двох випадкових величин. Умовні закони розподілу, умовне математичне очікування. Залежні та незалежні випадкові величини. Коефіцієнт кореляції. Вибірка. Обробка вибірки. Полігон та гістограма частот. Емпірична функція розподілу. Поняття оцінки параметрів розподілу. Вимоги до оцінки. Довірчий інтервал. Побудова інтервалів для оцінки математичного очікування та середнього квадратичного відхилення. Статистичні гіпотези. Критерії згоди. У додатках теорії ймовірностей основне значення має кількісна характеристика експерименту. Величина, яка може бути кількісно визначена і яка в результаті експерименту може приймати в залежності від випадку різні значення, називається випадковою величиною. Приклади випадкових величин: 1. Число випадань парного числа очок при десяти киданнях гральної кістки. 2. Кількість попадань у мету стрільцем, який здійснює серію пострілів. 3. Число осколків снаряда, що розірвався. У кожному з наведених прикладів випадкова величина може набувати лише ізольовані значення, тобто значення, які можна пронумерувати за допомогою натурального ряду чисел. Така випадкова величина, можливі значення якої є окремі ізольовані числа, які ця величина набуває з певними ймовірностями, називається дискретний. Число можливих значень дискретної випадкової величини може бути кінцевим або нескінченним (числовим). Законом розподілудискретної випадкової величини називають перелік її можливих значень та відповідних їм ймовірностей. Закон розподілу дискретної випадкової величини можна задати у вигляді таблиці (ряд розподілу ймовірностей), аналітично та графічно (багатокутник розподілу ймовірностей). При здійсненні того чи іншого експерименту виникає необхідність оцінювати величину, що вивчається, «в середньому». Роль середнього значення випадкової величини грає числова характеристика, що називається математичним очікуванням,яка визначається формулою де x 1 , x 2
,.. , x n– значення випадкової величини X, а p 1 ,p 2 ,
... , p n- ймовірності цих значень (зауважимо, що p 1
+
p 2
+…+
p n =
1). приклад. Здійснюється стрілянина по мішені (рис. 11). Попадання до I дає три очки, у II – два очки, у III – одне очко. Число очок, що вибиваються при одному пострілі одним стрільцем, має закон розподілу виду Для порівняння майстерності стрільців досить порівняти середні значення очок, що вибиваються, тобто. математичні очікування M(X) та M(Y):
M(X)
=
1
0,4
+ 2
0,2
+ 3
0,4
= 2,0, M(Y)
=
1
0,2
+ 2
0,5
+ 3
0,3
= 2,1. Другий стрілець дає у середньому дещо більше очок, тобто. при багаторазовій стрільбі він даватиме найкращий результат. Зазначимо властивості математичного очікування: 1. Математичне очікування постійної величини дорівнює самій постійній: M(C)
= C. 2. Математичне очікування суми випадкових величин дорівнює сумі математичних очікувань доданків: M =(X 1 +
X 2 +…+
X n)=
M(X 1)+
M(X 2)+…+
M(X n). 3. Математичне очікування твору взаємно незалежних випадкових величин дорівнює твору математичних очікувань змножувачів M(X 1 X 2 …
X n)
=
M(X 1)M(X 2)…
M(X n). 4. Математичне заперечення біномінального розподілу дорівнює добутку числа випробувань на ймовірність появи події в одному випробуванні (завдання 4.6). M(X)
= ін. Для оцінки того, як випадкова величина «у середньому» ухиляється від свого математичного очікування, тобто. щоб охарактеризувати розкид значень випадкової величини теорії ймовірностей служить поняття дисперсії. Дисперсієювипадкової величини Xназивають математичне очікування квадрата відхилення: D(X)
=
M[(X
-
M(X)) 2 ]. Дисперсія є числової характеристикою розсіювання випадкової величини. З визначення видно, що менше дисперсія випадкової величини, тим купальніше розташовуються її можливі значення біля математичного очікування, тобто краще значення випадкової величини характеризуються її математичним очікуванням. З визначення випливає, що дисперсія може бути обчислена за формулою Дисперсію зручно обчислювати за іншою формулою: D(X)
=
M(X 2)
- (M(X)) 2 .
Дисперсія має такі властивості: 1. Дисперсія постійної дорівнює нулю: D(C)
=
0.
2. Постійний множник можна виносити за знак дисперсії, зводячи його у квадрат: D(CX)
=
C 2 D(X). 3. Дисперсія суми незалежних випадкових величин дорівнює сумі дисперсії доданків: D(X 1 +
X 2 +
X 3 +…+
X n)=
D(X 1)+
D(X 2)+…+
D(X n) 4. Дисперсія біномного розподілу дорівнює добутку числа випробувань на ймовірність появи та непояви події в одному випробуванні: D(X)
= npq. Теоретично ймовірностей часто використовується числова характеристика, що дорівнює кореню квадратному з дисперсії випадкової величини. Ця числова характеристика називається середнім квадратним відхиленням та позначається символом Вона характеризує приблизний розмір ухилення випадкової величини від її середнього значення та має однакову з випадковою величиною розмірність. 4.1.
Стрілець проводить по мішені три постріли. Імовірність влучення в ціль при кожному пострілі дорівнює 0,3. Побудувати низку розподілу числа попадань. Рішення. Число влучень є дискретною випадковою величиною X. Кожному значенню x n
випадкової величини Xвідповідає певна ймовірність P n . Закон розподілу дискретної випадкової величини у разі можна задати поряд розподілу. У цій задачі Xприймає значення 0, 1, 2, 3. За формулою Бернуллі знайдемо ймовірність можливих значень випадкової величини: Р 3 (0)
= (0,7) 3 =
0,343, Р 3 (1)
= Р 3 (2)
= Р 3 (3)
= (0,3) 3 =
0,027. Розташувавши значення випадкової величини Xу зростаючому порядку отримаємо ряд розподілу: X n Зауважимо, що сума означає ймовірність того, що випадкова величина Xприйме хоча б одне значення з числа можливих, а ця подія є достовірною, тому 4.2
.В урні є чотири кулі з номерами від 1 до 4. Вийняли дві кулі. Випадкова величина X- Сума номерів куль. Побудувати низку розподілу випадкової величини X. Рішення.Значеннями випадкової величини Xє 3, 4, 5, 6, 7. Знайдемо відповідні ймовірності. Значення 3 випадкової величини Xможе приймати в одному випадку, коли одна з обраних куль має номер 1, а інший 2. Число всіляких результатів випробування дорівнює числу поєднань з чотирьох (число можливих пар куль) по два. За класичною формулою ймовірності отримаємо Аналогічно, Р(Х= 4) =Р(Х= 6) =Р(Х= 7) = 1/6. Сума 5 може з'явитися у двох випадках: 1 + 4 та 2 + 3, тому Хмає вигляд: Знайти функцію розподілу F(x) випадкової величини Xта побудувати її графік. Обчислити для Xїї математичне очікування та дисперсію. Рішення. Закон розподілу випадкової величини може бути заданий функцією розподілу F(x)
= P(X
x).
Функція розподілу F(x) - Незменшуюча, безперервна зліва функція, визначена на всій числовій осі, при цьому F
(-
)=
0,F
(+
)=
1. Для дискретної випадкової величини ця функція виражається формулою Тому в даному випадку Графік функції розподілу F(x) являє собою ступінчасту лінію (рис. 12) F(x) Математичне очікуванняМ(Х) є зваженою середньої арифметичної значень х 1 х 2 ,……х nвипадкової величини Хпри вагах ρ
1,
ρ
2, ……
, ρ
n
і називається середнім значенням випадкової величини Х. За формулою М(Х)= х 1
ρ
1 + х 2
ρ
2 + ……+ х n
ρ
n М(Х) = 3 · 0,14 +5 · 0,2 +7 · 0,49 +11 · 0,17 = 6,72. Дисперсіяхарактеризує ступінь розсіювання значень випадкової величини від свого середнього значення та позначається D(Х): D(Х)=М[(Х-М(Х)) 2 ]= М(Х 2)
–[М(Х)] 2 . Для дискретної випадкової величини дисперсія має вигляд або вона може бути обчислена за формулою Підставляючи числові дані завдання у формулу, отримаємо: М(Х 2)
=
3 2
∙ 0,14+5 2
∙ 0,2+7 2
∙ 0,49+11 2
∙ 0,17 = 50,84 D(Х)
= 50,84-6,72 2
= 5,6816. 4.4.
Дві гральні кістки одночасно кидають двічі. Написати біноміальний закон розподілу дискретної випадкової величини Х- Числа випадань парного сумарного числа очок на двох гральних кістках. Рішення. Введемо до розгляду випадкову подію А= (На двох кістках при одному киданні випало в сумі парне число очок). Використовуючи класичне визначення ймовірності, знайдемо Р(А)=
де n
- Число всіляких результатів випробування знаходимо за правилом множення: n
= 6∙6 =36, m
-
кількість сприятливих подій Арезультатів - одно m= 3∙6=18. Таким чином, ймовірність успіху в одному випробуванні дорівнює ρ
= Р(А)=
1/2.
Завдання вирішується із застосуванням схеми випробувань Бернуллі. Одним випробуванням тут буде кидання двох гральних кісток один раз. Число таких випробувань n
= 2. Випадкова величина Хприймає значення 0, 1, 2 з ймовірностями Р 2 (0)
= Шуканий біномінальний розподіл випадкової величини Хможна подати у вигляді ряду розподілу: х n ρ
n 4.5
. У партії із шести деталей є чотири стандартні. Навмання відібрано три деталі. Скласти розподіл ймовірностей дискретної випадкової величини Х– числа стандартних деталей серед відібраних та знайти її математичне очікування. Рішення.Значеннями випадкової величини Хє числа 0,1,2,3. Зрозуміло, що Р(Х=0)=0, оскільки нестандартних деталей лише дві. Р(Х=1) = Р(Х = 2) = Р(Х=3) = Закон розподілу випадкової величини Хпредставимо у вигляді ряду розподілу: х n ρ
n Математичне очікування М(Х)=1
∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2. 4.6
. Довести, що математичне очікування дискретної випадкової величини Х- Число появи події Ав nнезалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює ρ
- Так само твору числа випробувань на ймовірність появи події в одному випробуванні, тобто довести, що математичне очікування біномінального розподілу М(Х)
=n .
ρ
, а дисперсія D(X)
=np
. Рішення.Випадкова величина Хможе набувати значень 0, 1, 2…, n. Ймовірність Р(Х= к) знаходиться за формулою Бернуллі: Р(Х= до) = Р n(к)= Ряд розподілу випадкової величини Хмає вигляд: х n ρ
n q n де q=
1-
ρ
. Для математичного очікування маємо вираз: М(Х)= У разі одного випробування, тобто при n = 1для випадкової величини Х 1-числа появи події А- Ряд розподілу має вигляд: х n ρ
n M(X 1)=
0 ∙ q +
1
∙ p
=
p D(X 1)
=
p
–
p 2
=
p(1-
p)
=
pq. Якщо Хдо – кількість появи події Ав до-му випробуванні, то Р(Х до)=
ρ
і Х = Х 1 +Х 2 +….+Х n . Звідси отримуємо М(Х)=М(Х 1
)+М(Х 2)+
… +М(Х n)=
nρ,
D(X)=D(X 1)+D(X 2)+
...
+D(X n)= npq. 4.7.
ВТК перевіряє вироби на стандартність. Імовірність того, що виріб стандартний, дорівнює 0,9. Кожна партія містить 5 виробів. Знайти математичне очікування дискретної випадкової величини Х- числа партій, у кожній з яких виявиться одно 4 стандартні вироби – якщо перевірці підлягає 50 партій. Рішення. Імовірність того, що в кожній довільно обраній партії виявиться 4 стандартні вироби, постійна; позначимо її через ρ
. Тоді математичне очікування випадкової величини Ходно М(Х)=
50∙ρ.
Знайдемо ймовірність ρ
за формулою Бернуллі: ρ=Р 5 (4)= М(Х)=
50∙0,32=16. 4.8
. Впадають три гральні кістки. Знайти математичне очікування суми очок, що випали. Рішення.Можна знайти розподіл випадкової величини Х- суми очок, що випали, а потім її математичне очікування. Однак такий шлях надто громіздкий. Простіше використовувати інший прийом, представляючи випадкову величину Х, математичне очікування якої потрібно обчислити, як суми кількох більш простих випадкових величин, математичне очікування яких обчислити легше. Якщо випадкова величина Х i- Це число очок, що випали на i- й кістки ( i= 1, 2, 3), то сума очок Хвисловиться у вигляді Х = Х 1 + Х 2 + Х 3 . Для обчислення математичного очікування вихідної випадкової величини залишиться лише скористатися властивістю математичного очікування М(Х 1
+ Х 2 + Х 3
)= М(Х 1
)+ М(Х 2)+ М(Х 3
). Очевидно, що Р(Х i = До)=
1/6, К=
1, 2, 3, 4, 5, 6,
i=
1,
2, 3. Отже, математичне очікування випадкової величини Х iмає вигляд М(Х i)
=
1/6∙1
+ 1/6∙2
+1/6∙3
+ 1/6∙4
+ 1/6∙5
+ 1/6∙6
= 7/2, М(Х)
=
3∙7/2 = 10,5.
4.9.
Визначити математичне очікування кількості приладів, які відмовили в роботі за час випробувань, якщо: а) ймовірність відмови для всіх приладів одна і та ж дорівнює р, а кількість випробуваних приладів дорівнює n; б) ймовірність відмови для i
–
го приладу дорівнює p i
,
i=
1,
2, … , n. Рішення.Нехай випадкова величина Х– кількість приладів, що відмовили, тоді Х = Х 1 + Х 2 + … + Х n ,
X i
=
Зрозуміло, що Р(Х i =
1)=
Р i ,
Р(Х i =
0)=
1–
Р i ,i= 1,
2,
…
,n. М(Х i)=
1∙Р i +
0∙(1-Р i)=Р i , М(Х)=М(Х 1)+М(Х 2)+ … +М(Х n)=Р 1 +Р 2 + … +Р n .
У разі «а» ймовірність відмови приладів одна й та сама, тобто Р i =p,i= 1,
2, …
,n. М(Х)=
np. Цю відповідь можна було отримати відразу, якщо помітити, що випадкова величина Хмає біномний розподіл з параметрами ( n,
p).
4.10.
Дві гральні кістки кидають одночасно двічі. Написати біноміальний закон розподілу дискретної випадкової величини Х -числа випадання парного числа очок на двох гральних кістках Рішення. Нехай А= (Випадання парного числа на першій кістці), В =(Випадання парного числа на другий кістки). Випадання парного числа на обох кістках при одному киданні висловиться твором АВ.Тоді Р
(АВ)
= Р(А)∙Р(У)
=
Результат другого кидання двох гральних кісток не залежить від першого, тому застосовна формула Бернуллі при n
=
2,р = 1/4,
q
=
1- р = 3/4.
Випадкова величина Хможе приймати значення 0, 1, 2 ,
ймовірність яких знайдемо за формулою Бернуллі: Р(Х = 0)= Р 2
(0)
=
q
2
= 9/16, Р(Х = 1)= Р 2
(1)= З Р(Х = 2)= Р 2
(2)= З Ряд розподілу випадкової величини Х: 4.11.
Пристрій складається з великої кількості незалежно працюючих елементів з однаковою дуже малою ймовірністю відмови кожного елемента за час t. Знайти середню кількість тих, хто відмовився за час tелементів, якщо ймовірність того, що за цей час відмовить хоч один елемент, дорівнює 0,98. Рішення.
Кількість тих, хто відмовив за час tелементів – випадкова величина Х, Яка розподілена за законом Пуассона, оскільки число елементів велике, елементи працюють незалежно і можливість відмови кожного елемента мала. Середня кількість появи події в nвипробуваннях одно М(Х)
=
np.
Оскільки ймовірність відмови Доелементів з nвиражається формулою Р n
(До)
де
=
np, то ймовірність того, що не відмовить жоден елемент за час t
отримаємо при К = 0: Р n
(0)= е - . Тому ймовірність протилежної події – за час t
відмовить хоча б один елемент - 1 - е -
. За умовою завдання ця ймовірність дорівнює 0,98. З рівняння 1
- е -
= 0,98, е -
= 1 – 0,98 =
0,02, звідси
=
-ln
0,02
4. Отже, за час tроботи пристрою відмовить у середньому 4 елементи. 4.12
. Гральна кістка кидається до того часу, поки не випаде «двійка». Знайти середню кількість кидань. Рішення. Введемо випадкову величину Х- Число випробувань, яке треба зробити, поки що цікавить нас подія не настане. Імовірність того, що Х= 1 дорівнює ймовірності те, що з одному киданні кістки випаде «двійка», тобто. Р(Х = 1)
= 1/6. Подія Х= 2 означає, що з першому випробуванні «двійка» не випала, а за другому випала. Ймовірність події Х= 2 знаходимо за правилом множення ймовірностей незалежних подій: Р(Х = 2)
= (5/6)∙(1/6) Аналогічно, Р(Х = 3)
= (5/6) 2 ∙1/6, Р(Х = 4)
= (5/6) 2 ∙1/6 і т.д. Отримаємо низку розподілу ймовірностей: (5/6) до
∙1/6 Середня кількість кидань (випробувань) є математичне очікування М(Х)
=
1∙1/6 +
2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6
+ … + До
(5/6) До -1 ∙1/6
+ … = 1/6∙(1+2∙5/6 +3∙(5/6) 2
+ … + До
(5/6) До -1
+ …) Знайдемо суму ряду: Отже, М(Х)
=
(1/6) (1/ (1 –
5/6) 2
= 6. Таким чином, потрібно здійснити в середньому 6 кидань гральної кістки доти, доки не випаде «двійка». 4.13.
Виробляються незалежні випробування з однаковою ймовірністю появи події Ау кожному випробуванні. Знайти ймовірність появи події А, якщо дисперсія числа події у трьох незалежних випробуваннях дорівнює 0,63 .
Рішення.Число появи події у трьох випробуваннях є випадковою величиною Х, розподіленою за біноміальним законом. Дисперсія числа події у незалежних випробуваннях (з однаковою ймовірністю появи події у кожному випробуванні) дорівнює добутку числа випробувань на ймовірності появи та непояви події (завдання 4.6) D(Х)
=
npq.
За умовою n
=
3,
D(Х)
=
0,63, тому можна рзнайти з рівняння 0,63
= 3∙р(1-р), яке має два рішення р 1
=
0,7 та р 2
=
0,3.

 1.2.
р4 = 0,1; 0 при х≤-1,
1.2.
р4 = 0,1; 0 при х≤-1,

 (Рис.5)
(Рис.5) https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 при х≤а,
https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 при х≤а, ,
, Нормальна крива симетрична щодо прямої х=m, має максимум т. х=а, рівний .
Нормальна крива симетрична щодо прямої х=m, має максимум т. х=а, рівний .
![]() ,
,![]()
![]()

Рішення.
Імовірність того, що не випало жодного герба: P(0) = 0,5*0,5*0,5= 0,125
P(1) = 0,5
*0,5*0,5 + 0,5*0,5
*0,5 + 0,5*0,5*0,5
= 3*0,125=0,375
P(2) = 0,5
*0,5
*0,5 + 0,5
*0,5*0,5
+ 0,5*0,5
*0,5
= 3*0,125=0,375
Імовірність того, що випало три герби: P(3) = 0,5*0,5*0,5 = 0,125
Перевірка: P = P (0) + P (1) + P (2) + P (3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 X 0
1
2
3
P 0,125
0,375
0,375
0,125
Рішення.
Розглянемо подію A – одне влучення в ціль. Можливі варіанти настання цієї події такі:
Тоді ймовірність події А – рівно одне влучення в ціль, дорівнюватиме: P(A) = 0.12+0.17+0.68 = 0.97 ![]() , З якими випадкова величина набуває кожного із значень, тобто.
, З якими випадкова величина набуває кожного із значень, тобто. ![]() .
.Значення
...
Ймовірність
...
![]() є несумісними та єдино можливими: вони утворюють повну систему подій. Тому сума їх ймовірностей дорівнює одиниці:
є несумісними та єдино можливими: вони утворюють повну систему подій. Тому сума їх ймовірностей дорівнює одиниці:![]() .
.Сума виграшу -100
900
2900
Ймовірність 0,94
0,04
0,02
Функція розподілу дискретної випадкової величини: побудова
![]() , Що визначає ймовірність, що значення випадкової величини Xменше або дорівнює граничному значенню х.
, Що визначає ймовірність, що значення випадкової величини Xменше або дорівнює граничному значенню х.Значення 1
2
3
4
5
6
Ймовірність 1/6
1/6
1/6
1/6
1/6
1/6

Значення 0
1
2
3
Ймовірність 1/30
3/10
1/2
1/6
![]() . При
. При
Функція розподілу дискретної випадкової величини: обчислення
Тривалість шлюбу (років) Число Ймовірність F(x)
0
10
0,002
0,002
1
80
0,013
0,015
2
177
0,029
0,044
3
209
0,035
0,079
4
307
0,051
0,130
5
335
0,056
0,186
6
358
0,060
0,246
7
413
0,069
0,314
8
432
0,072
0,386
9
402
0,067
0,453
10 і більше 3287
0,547
1,000
Усього 6010
1
Зв'язок закону розподілу дискретної випадкової величини з математичним очікуванням та дисперсією
 (1)
(1)
![]() , (2)
, (2)![]() .
.![]()

![]() ,
,



ДОДАТОК
Елементи комбінаторики

Дії над подіями
 ;
; ;
;
Класичне визначення ймовірності
 , які сприяють появі події Адо загальної кількості дослідів
, які сприяють появі події Адо загальної кількості дослідів  :
:
Формула множення ймовірностей
 можна знайти за формулою:
можна знайти за формулою: - ймовірність події А,
- ймовірність події А, - ймовірність події В,
- ймовірність події В, - ймовірність події Уза умови, що подія Авже сталося.
- ймовірність події Уза умови, що подія Авже сталося.
Формула складання ймовірностей
 можна знайти за формулою:
можна знайти за формулою: - ймовірність спільної появи подій Аі У.
- ймовірність спільної появи подій Аі У.
Формула повної ймовірності
 ,
,
 ,
…,
,
…,
 - Назвемо їх гіпотезами. Також відомі
- Назвемо їх гіпотезами. Також відомі  - ймовірність виконання i-ой гіпотези та
- ймовірність виконання i-ой гіпотези та  - ймовірність появи події А під час виконання i-ой гіпотези. Тоді ймовірність події Аможе бути знайдена за формулою:
- ймовірність появи події А під час виконання i-ой гіпотези. Тоді ймовірність події Аможе бути знайдена за формулою:
Схема Бернуллі

 у схемі Бернуллі – це кількість появи деякої події, якій відповідає найбільша ймовірність. Можна знайти за формулою:
у схемі Бернуллі – це кількість появи деякої події, якій відповідає найбільша ймовірність. Можна знайти за формулою:
Випадкові величини
Числові характеристики дискретних випадкових величин
Х



Р



Функція розподілу
Питання до іспиту

 .
.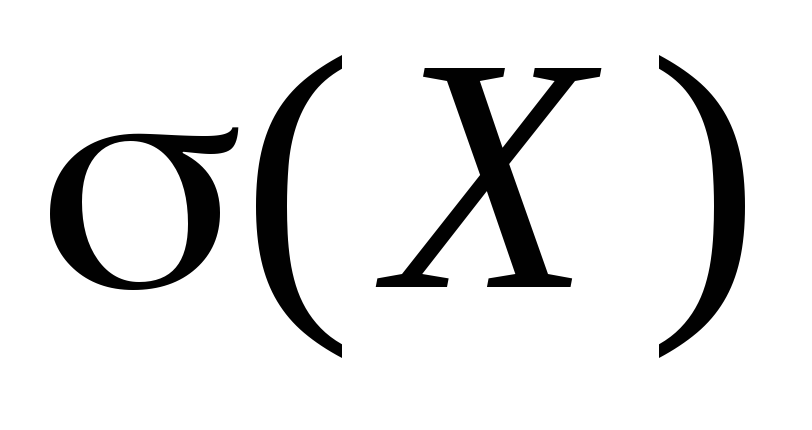 .
. ,
, 0,3(0,7) 2
= 0,441,
0,3(0,7) 2
= 0,441, (0,3) 2 0,7
= 0,189,
(0,3) 2 0,7
= 0,189,

 .
.
 .
. .
.

 ,
,
 ,Р 2 (1)
=
,Р 2 (1)
= ∙
∙ ,Р 2 (2)
=
,Р 2 (2)
=
 =1/5,
=1/5, = 3/5,
= 3/5, = 1/5.
= 1/5.
 ρ
до
(1-ρ
) n-до
ρ
до
(1-ρ
) n-до
 ρq n- 1
ρq n- 1
 ρq n- 2
ρq n- 2
 ρ
n
ρ
n ρq n -
1
+2
ρq n -
1
+2
 ρ
2
q n -
2
+…+.n
ρ
2
q n -
2
+…+.n
 ρ
n
ρ
n
 = 0,94∙0,1=0,32.
= 0,94∙0,1=0,32.
 .
. ,р∙q
=
6/16,
,р∙q
=
6/16, ,
р 2
=
1/16.
,
р 2
=
1/16.
 ,
,
 Доg
До -1
= (
Доg
До -1
= ( g До)
g
g До)
g
 .
.







