Схема повторних незалежних випробувань. Формула Бернуллі. Схема Бернуллі. Приклади розв'язання задач

Повторні незалежні випробування називаються випробуваннями Бернуллі, якщо кожне випробування має лише два можливі результати та ймовірності результатів залишаються незмінними для всіх випробувань.

Зазвичай ці два результати називаються "успіхом" (У) або "невдачею" (Н) і відповідні ймовірності позначають pі q. Зрозуміло, що p 0, q³ 0 та p+q=1.

Простір елементарних подій кожного випробування складається із двох подій У та Н.

Простір елементарних подій nвипробувань Бернуллі Ω містить 2 nелементарних подій, що являють собою послідовності (ланцюжки) з nсимволів У та Н. Кожна елементарна подія є одним із можливих результатів послідовності nвипробувань Бернуллі. Оскільки випробування незалежні, то, за теоремою множення, ймовірності перемножуються, тобто ймовірність будь-якої конкретної послідовності є твір, отриманий при заміні символів У і Н на pі qвідповідно, тобто, наприклад: Р( )=(У У Н У Н ... Н У )= p p q p q ... q q p .

Зазначимо, результат випробування Бернуллі часто позначають 1 і 0 і тоді елементарна подія в послідовності nвипробувань Бернуллі - є ланцюжок, що складається з нулів та одиниць. Наприклад:  =(1, 0, 0, ..., 1, 1, 0).

Випробування Бернуллі є найважливішою схемою, що розглядається в теорії ймовірностей. Ця схема названа на честь швейцарського математика Я. Бернуллі (1654-1705), які у своїх роботах глибоко досліджували цю модель.

Основне завдання, яке нас буде тут цікавити: яка ймовірність тієї події, що в nвипробуваннях Бернуллі відбулося mуспіхів?

За виконання зазначених умов ймовірність того, що при проведенні незалежних випробувань подія спостерігатиметься рівно m раз (неважливо, у яких саме дослідах), визначається за формулі Бернуллі:

(21.1)

де - ймовірність появи у кожному випробуванні, а
- ймовірність того, що в цьому досвіді подія не відбулося.

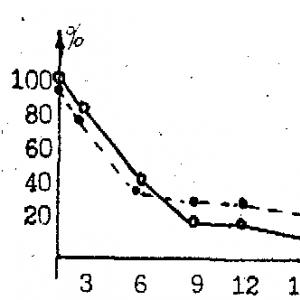
Якщо розглядати P n (m)як функцію m, вона задає розподіл ймовірностей, яке називається биномиальным. Досліджуємо цю залежність P n (m)від m, 0£ m£ n.

Події B m ( m = 0, 1, ..., n), які перебувають у різному числіпояви події Ав nвипробування, несумісні і утворюють повну групу. Отже,
.

Розглянемо співвідношення:

=
=
=
.

Звідси слідує що P n (m+1))>P n (m),якщо (n- m)p> (m+1)q, тобто. функція P n (m) зростає, якщо m< np- q. Аналогічно, P n (m+1)< P n (m),якщо (n- m)p< (m+1)q, тобто. P n (m)зменшується, якщо m> np- q.

Таким чином, існує число m 0 ,при якому P n (m)сягає найбільшого значення. Знайдемо m 0 .

За змістом числа m 0 маємо P n (m 0)³ P n (m 0 -1) та P n (m 0) ³ P n (m 0 +1), звідси

, (21.2)

. (21.3)

Вирішуючи нерівності (21.2) та (21.3) щодо m 0 , отримуємо:

p/ m 0 ³ q/(n- m 0 +1) Þ m 0 £ np+ p,

q/(n- m 0 ) ³ p/(m 0 +1) Þ m 0 ³ np- q.

Отже, потрібне число m 0 задовольняє нерівностям

np- q£ m 0 £ np+p. (21.4)

Так як p+q=1, то довжина інтервалу, що визначається нерівністю (21.4), дорівнює одиниці і є, принаймні, одне ціле число m 0 , що задовольняє нерівності (21.4):

1) якщо np - q- ціле число, тобто два значення m 0 , а саме: m 0 = np - qі m 0 = np - q + 1 = np + p;

2) якщо np - q- дробове, то існує одне число m 0 , а саме єдине ціле, укладене між дробовими числамиотриманими з нерівності (21.4);

3) якщо np- ціле число, то існує одне число m 0 , а саме m 0 = np.

Число m 0 називається найбільш ймовірним або найімовірнішим значенням (числом) появи події Aу серії з nнезалежних випробувань.

На цьому уроці знаходимо ймовірність настання події у незалежних випробуваннях при повторенні випробувань . Випробування називаються незалежними, якщо ймовірність того чи іншого результату кожного випробування не залежить від того, які результати мали інші випробування . Незалежні випробування можуть проводитися як у однакових умовах, і у різних. У першому випадку ймовірність появи деякої події у всіх випробуваннях одна й та сама, у другому випадку вона змінюється від випробування до випробування.

Приклади незалежних повторних випробувань :

• вийде з ладу один із вузлів приладу або два, три вузли, причому вихід з ладу кожного вузла не залежить від іншого вузла, а ймовірність виходу з ладу одного вузла постійна у всіх випробуваннях;
• вироблена в деяких постійних технологічних умовах деталь, або три, чотири, п'ять деталей, виявляться нестандартними, причому одна деталь може виявитися нестандартною незалежно від будь-якої іншої деталі та ймовірність того, що деталь виявиться нестандатною, постійна у всіх випробуваннях;
• з кількох пострілів по мішені один, три чи чотири постріли потрапляють у мету незалежно від наслідків інших пострілів і можливість попадання в ціль постійна у всіх випробуваннях;
• при опусканні монети автомат спрацює правильно один, два чи інше число разів незалежно від того, який результат мали інші опускання монети, і можливість того, що автомат спрацює правильно, постійна у всіх випробуваннях.

Ці події можна описати однією схемою. Кожна подія настає у кожному випробуванні з однією і тією ж ймовірністю, яка не змінюється, якщо стають відомими результати попередніх випробувань. Такі випробування називаються незалежними, а схема називається схемою Бернуллі . Передбачається, що такі випробування можуть бути повторені як завгодно велика кількістьразів.

Якщо ймовірність pнастання події Aу кожному випробуванні постійна, то ймовірність того, що в nнезалежних випробуваннях подія Aнастане mраз, знаходиться по формулі Бернуллі :

(де q= 1 – p- ймовірність того, що подія не настане)

Поставимо завдання – знайти ймовірність того, що подія такого типу nнезалежних випробуваннях настане mразів.

Формула Бернуллі: приклади розв'язання задач

приклад 1.Знайти ймовірність того, що серед взятих випадково п'яти деталей дві стандартні, якщо ймовірність того, що кожна деталь виявиться стандартною, дорівнює 0,9.

Рішення. Ймовірність події А, Що полягає в тому, що взята випадково деталь стандартна, є p=0,9 , а ймовірність того, що вона нестандартна, є q=1–p= 0,1. Позначена в умові завдання подія (позначимо її через У) настане, якщо, наприклад, перші дві деталі виявляться стандартними, а наступні три – нестандартними. Але подія Утакож настане, якщо перша та третя деталі виявляться стандартними, а решта – нестандартними, або якщо друга та п'ята деталі будуть стандартними, а решта – нестандартними. Є й інші можливості настання події У. Кожна з них характеризується тим, що з п'яти деталей дві, що займають будь-які місця з п'яти, виявляться стандартними. Отже, загальне числорізних можливостей настання події Удорівнює кількості можливостей розміщення на п'яти місцях двох стандартних деталей, тобто. дорівнює кількості поєднань з п'яти елементів по два, а .

Імовірність кожної з можливостей по теоремі множення ймовірностей дорівнює добутку п'яти множників, у тому числі два, відповідні появі стандартних деталей, рівні 0,9, інші три, відповідні появі нестандартних деталей, рівні 0,1, тобто. ця ймовірність становить. Так як зазначені десять можливостей є несумісними подіями, за теоремою складання ймовірність події У, яку позначимо

приклад 2.Імовірність того, що верстат протягом години вимагатиме уваги робітника, дорівнює 0,6. Припускаючи, що неполадки на верстатах незалежні, знайти ймовірність того, що протягом години уваги робітника вимагатиме якийсь один верстат із чотирьох обслуговуваних ним.

Рішення. Використовуючи формулу Бернулліпри n=4 , m=1 , p=0,6 та q=1–p=0,4 , отримаємо

приклад 3.Для нормальної роботиавтобази на лінії має бути не менше восьми автомашин, а їх є десять. Можливість невиходу кожної машини на лінію дорівнює 0,1. Знайти можливість нормальної роботи автобази в найближчий день.

Рішення. Автобаза працюватиме нормально (подія F), якщо на лінію вийдуть чи вісім (подія А), або дев'ять (подія У), або всі десять автомашин подія (подія C). За теоремою складання ймовірностей,

Кожен доданок знаходимо за формулою Бернуллі. Тут n=10 , m=8; 10 , а p=1-0,1=0,9, оскільки pмає означати можливість виходу автомашини на лінію; тоді q= 0,1. В результаті отримаємо

приклад 4.Нехай ймовірність того, що покупцю необхідне чоловіче взуття 41-го розміру, дорівнює 0,25. Знайти ймовірність того, що із шести покупців принаймні двом необхідне взуття 41-го розміру.

Коротка теорія

Теорія ймовірностей має справу з такими експериментами, які можна повторювати (принаймні теоретично) необмежену кількість разів. Нехай деякий експеримент повторюється в один раз, причому результати кожного повторення не залежать від результатів попередніх повторень. Такі серії повторень називають незалежними випробуваннями. Окремим випадком таких випробувань є незалежні випробування Бернуллі, які характеризуються двома умовами:

1) результатом кожного випробування є один із двох можливих результатів, званих відповідно «успіхом» або «невдачею».

2) ймовірність «успіху», у кожному наступному випробуванні не залежить від результатів попередніх випробувань та залишається постійною.

Теорема Бернуллі

Якщо проводиться серія з незалежних випробувань Бернуллі, у кожному з яких «успіх» з'являється з ймовірністю, то ймовірність того, що «успіх» у випробуваннях з'явиться рівно раз, виражається формулою:

де – ймовірність «невдачі».

- Число поєднань елементів по (див. основні формули комбінаторики)

Ця формула називається формулою Бернуллі.

Формула Бернуллі дозволяє позбавитися великої кількості обчислень - складання та множення ймовірностей - при досить великій кількості випробувань.

Схему випробувань Бернуллі називають також біномною схемою, а відповідні ймовірності – біноміальними, що пов'язано з використанням біномних коефіцієнтів.

Розподіл за схемою Бернуллі дозволяє, зокрема, знайти найімовірніше число настання події.

Якщо кількість випробувань nвелике, то користуються:

Приклад розв'язання задачі

Умова задачі

Схожість насіння деякої рослини становить 70%. Яка ймовірність того, що з 10 посіяних насіння зійдуть: 8, принаймні 8; не менше 8?

Рішення завдання

Скористаємося формулою Бернуллі:

У нашому випадку

Нехай подія – з 10 насінин зійдуть 8:

Нехай подія зійде принаймні 8 (це означає 8, 9 або 10)

Нехай подія зійде не менше 8 (це означає 8,9 або 10)

Відповідь

Середнявартість рішення контрольної роботи 700 - 1200 рублів (але не менше 300 руб. за все замовлення). На ціну сильно впливає терміновість рішення (від доби до кількох годин). Вартість онлайн-допомоги на іспиті/заліку – від 1000 руб. за рішення квитка.

Заявку можна залишити прямо в чаті, попередньо скинувши умову завдань та повідомивши необхідні вам терміни вирішення. Час відповіді – кілька хвилин.

Визначення повторних незалежних випробувань. Формули Бернуллі для обчислення ймовірності та найімовірнішого числа. Асимптотичні формули для формули Бернуллі (локальна та інтегральна, теореми Лапласа). Використання інтегральної теореми. Формула Пуассона для малоймовірних випадкових подій.

Повторні незалежні випробування

На практиці доводиться стикатися з такими завданнями, які можна представити у вигляді випробувань, що багаторазово повторюються, в результаті кожного з яких може з'явитися або не з'явитися подія A . При цьому інтерес представляє результат не кожного окремого випробування, а Загальна кількістьпояви події A в результаті певної кількості випробувань. У таких завданнях потрібно вміти визначати ймовірність будь-якого числа m появи події A в результаті n випробувань. Розглянемо випадок, коли випробування є незалежними та ймовірність появи події A у кожному випробуванні постійна. Такі випробування називаються повторними незалежними.

Прикладом незалежних випробувань може бути перевірка на придатність виробів, взятих однією з низки партій. Якщо в цих партіях відсоток шлюбу однаковий, то ймовірність того, що вибраний виріб буде бракованим, у кожному випадку є постійним числом.

Формула Бернуллі

Скористаємося поняттям складної події, Під яким мається на увазі поєднання кількох елементарних подій, що перебувають у появі або непояві події A в i -му випробуванні. Нехай проводиться n незалежних випробувань, у кожному з яких подія A може з'явитися з ймовірністю p , або не з'явитися з ймовірністю q = 1-p . Розглянемо подію B_m , що полягає в тому, що подія A в цих n випробуваннях настане рівно m разів і, отже, не настане рівно (n-m) разів. Позначимо A_i~(i=1,2,\ldots,(n))поява події A , a \overline(A)_i - непоява події A в i-му випробуванні. В силу сталості умов випробування маємо

Подія A може з'явитися m разів у різних послідовностях або комбінаціях, чергуючись із протилежною подією \overline(A) . Число можливих комбінацій такого роду дорівнює числу поєднань з n елементів по m, тобто C_n^m. Отже, подію B_m можна у вигляді суми складних несумісних між собою подій, причому кількість доданків дорівнює C_n^m :

B_m=A_1A_2\cdots(A_m)\overline(A)_(m+1)\cdots\overline(A)_n+cdots+\overline(A)_1\overline(A)_2\cdots\overline(A)_( n-m)A_(n-m+1)\cdots(A_n),

де кожен добуток подія A входить m разів, а \overline(A) - (n-m) разів.

Імовірність кожної складної події, що входить у формулу (3.1), з теореми множення ймовірностей для незалежних подій дорівнює p^(m)q^(n-m) . Оскільки загальна кількість подій дорівнює C_n^m , то, використовуючи теорему складання ймовірностей для несумісних подій, отримуємо ймовірність події B_m (позначимо її P_(m,n) )

P_(m,n)=C_n^mp^(m)q^(n-m)\quad \text(or)\quad P_(m,n)=\frac(n{m!(n-m)!}p^{m}q^{n-m}. !}

Формулу (3.2) називають формулою Бернуллі, а випробування, що повторюються, задовольняють умові незалежності і сталості ймовірностей появи в кожному з них події A , називають випробуваннями Бернулліабо схемою Бернуллі.

Приклад 1. Імовірність виходу за межі поля допуску при обробці деталей токарному верстатідорівнює 0,07. Визначити ймовірність того, що з п'яти навмання відібраних протягом зміни деталей в однієї розміри діаметра не відповідають заданому допуску.

Рішення. Умова завдання відповідає вимогам схеми Бернуллі. Тому, вважаючи n=5,\,m=1,\,p=0,\!07, за формулою (3.2) отримуємо

P_(1,5)=C_5^1(0,\!07)^(1)(0,\!93)^(5-1)\approx0,\!262.

Приклад 2. Спостереженнями встановлено, що у певній місцевості у вересні буває 12 дощових днів. Яка ймовірність того, що з випадково взятих цього місяця 8 днів 3 дні виявляться дощовими?

Рішення.

P_(3;8)=C_8^3(\left(\frac(12)(30)\right)\^3{\left(1-\frac{12}{30}\right)\!}^{8-3}=\frac{8!}{3!(8-3)!}{\left(\frac{2}{5}\right)\!}^3{\left(\frac{3}{5}\right)\!}^5=56\cdot\frac{8}{125}\cdot\frac{243}{3125}=\frac{108\,864}{390\,625}\approx0,\!2787. !}

Найімовірніше число події

Найімовірнішим числом появиподії A в n незалежних випробуваннях називається таке число m_0 , для якого ймовірність, що відповідає цій кількості, перевищує або, принаймні, не менше ймовірності кожного з інших можливих чисел появи події A . Для визначення найбільш ймовірного числа не обов'язково обчислювати ймовірності можливих чисел появи події, достатньо знати число випробувань n і ймовірність появи події A в окремому випробуванні. Позначимо P_(m_0,n) ймовірність, що відповідає найімовірнішому числу m_0 . Використовуючи формулу (3.2), записуємо

P_(m_0,n)=C_n^(m_0)p^(m_0)q^(n-m_0)=\frac(n{m_0!(n-m_0)!}p^{m_0}q^{n-m_0}. !}

Згідно з визначенням найімовірнішого числа, ймовірності настання події A відповідно m_0+1 і m_0-1 разів повинні, принаймні, не перевищувати ймовірність P_(m_0,n) , тобто.

P_(m_0,n)\geqslant(P_(m_0+1,n));\quad P_(m_0,n)\geqslant(P_(m_0-1,n))

Підставляючи в нерівності значення P_(m_0,n) та виразу ймовірностей P_(m_0+1,n) та P_(m_0-1,n) , отримуємо

Вирішуючи ці нерівності щодо m_0, отримуємо

M_0\geqslant(np-q),\quad m_0\leqslant(np+p)

Об'єднуючи останні нерівності, отримуємо подвійну нерівність, яку використовують для визначення найімовірнішого числа:

Np-q \ leqslant (m_0) \ leqslant (np + p).

Оскільки довжина інтервалу, що визначається нерівністю (3.4), дорівнює одиниці, тобто.

(np+p)-(np-q)=p+q=1,

і подія може відбутися в n випробуваннях тільки ціле число разів, слід мати на увазі, що:

1) якщо np-q - ціле число, то існують два значення найімовірнішого числа, а саме: m_0=np-q і m"_0=np-q+1=np+p;

2) якщо np-q - дробове число, то існує одне найбільш ймовірне число, а саме: єдине ціле, укладене між дробовими числами, отриманими з нерівності (3.4);

3) якщо np - ціле число, то існує одне найімовірніше число, а саме: m_0 = np.

При великих значеннях n користуватися формулою (3.3) для розрахунку ймовірності, що відповідає найімовірнішому числу, незручно. Якщо у рівність (3.3) підставити формулу Стірлінга

N!\approx(n^ne^(-n)\sqrt(2\pi(n))),

справедливу для досить великих n і прийняти найімовірніше число m_0=np , то отримаємо формулу для наближеного обчислення ймовірності, що відповідає найімовірнішому числу:

P_(m_0,n)\approx\frac(n^ne^(-n)\sqrt(2\pi(n))\,p^(np)q^(nq))((np)^(np) e^(-np)\sqrt(2\pi(np))\,(nq)^(nq)e^(-nq)\sqrt(2\pi(nq)))=\frac(1)(\ sqrt(2pi(npq)))=frac(1)(sqrt(2pi)sqrt(npq)).

Приклад 2. Відомо, що частина продукції, що поставляється заводом на торговельну базу \frac(1)(15), не задовольняє всім вимогам стандарту. На базу було завезено партію виробів у кількості 250 шт. Знайти найімовірніше число виробів, що задовольняють вимогам стандарту, і обчислити ймовірність того, що в цій партії виявиться найімовірніше число виробів.

Рішення. За умовою n=250,\,q=\frac(1)(15),\,p=1-\frac(1)(15)=\frac(14)(15). Відповідно до нерівності (3.4) маємо

250\cdot\frac(14)(15)-\frac(1)(15)\leqslant(m_0)\leqslant250\cdot\frac(14)(15)+\frac(1)(15)

звідки 233 \ 26 \ leqslant (m_0) \ leqslant234 \ 26. Отже, найімовірніше число виробів, які відповідають вимогам стандарту, у партії з 250 шт. 234. Підставляючи дані у формулу (3.5), обчислюємо ймовірність наявності в партії найімовірнішого числа виробів:

P_(234,250)\approx\frac(1)(\sqrt(2\pi\cdot250\cdot\frac(14)(15)\cdot\frac(1)(15)))\approx0,\!101

Локальна теорема Лапласа

Користуватися формулою Бернуллі при великих значеннях дуже важко. Наприклад, якщо n=50,\,m=30,\,p=0,\!1, то знаходження ймовірності P_(30,50) треба обчислити значення висловлювання

P_(30,50)=\frac(50{30!\cdot20!}\cdot(0,\!1)^{30}\cdot(0,\!9)^{20} !}

Природно, виникає питання: чи не можна обчислити ймовірність, що цікавить, не використовуючи формулу Бернуллі? Виявляється, можна. Локальна теорема Лапласа дає асимптотичну формулу, яка дозволяє приблизно знайти ймовірність появи подій рівно m разів у n випробуваннях, якщо число випробувань досить велике.

Теорема 3.1. Якщо ймовірність p появи події A в кожному випробуванні постійна і відмінна від нуля і одиниці, то ймовірність P_(m,n) того, що подія A з'явиться в n випробуваннях рівно m разів, приблизно дорівнює (тим точніше, ніж більше n) значення функції

Y=\frac(1)(\sqrt(npq))\frac(e^(-x^2/2))(\sqrt(2\pi))=\frac(\varphi(x))(\sqrt (npq))при .

Існують таблиці, які містять значення функції \varphi(x)=\frac(1)(\sqrt(2\pi))\,e^(-x^2/2)), Що відповідають позитивним значенням аргументу x. Для негативних значеньаргументу використовують самі таблиці, оскільки функція \varphi(x) парна, тобто. \varphi(-x)=\varphi(x).

Отже, приблизно ймовірність того, що подія A з'явиться в n випробуваннях рівно m разів,

P_(m,n)\approx\frac(1)(\sqrt(npq))\,\varphi(x),де x = frac (m-np) (sqrt (npq)).

Приклад 3. Знайти ймовірність того, що подія A настане рівно 80 разів у 400 випробуваннях, якщо ймовірність появи події A у кожному випробуванні дорівнює 0,2.

Рішення. За умовою n=400,\,m=80,\,p=0,\!2,\,q=0,\!8. Скористаємося асимптотичною формулою Лапласа:

P_(80,400)\approx\frac(1)(\sqrt(400\cdot0,\!2\cdot0,\!8))\,\varphi(x)=\frac(1)(8)\,\varphi (x).

Обчислимо визначуване даними завдання значення x :

X = frac (m-np) (sqrt (npq)) = frac (80-400 cdot0,! 2) (8) = 0.

За таблицею дод, 1 знаходимо \varphi(0)=0,\!3989. Шукана ймовірність

P_ (80,100) = frac (1) (8) cdot0, 3989 = 0, 04986.

Формула Бернуллі призводить приблизно до такого ж результату (викладки через їхню громіздкість опущені):

P_ (80,100) = 0, \!0498.

Інтегральна теорема Лапласа

Припустимо, що проводиться n незалежних випробувань, у кожному з яких ймовірність появи події A є постійною і дорівнює p . Необхідно обчислити ймовірність P_((m_1,m_2),n) того, що подія A з'явиться в n випробуваннях не менше m_1 і не більше m_2 разів (для стислості говоритимемо "від m_1 до m_2 разів"). Це можна зробити за допомогою інтегральної теореми Лапласа.

Теорема 3.2. Якщо ймовірність p наступу події A у кожному випробуванні постійна і відмінна від нуля і одиниці, то приблизно ймовірність P_((m_1,m_2),n) того, що подія A з'явиться у випробуваннях від m_1 до m_2 разів,

P_((m_1,m_2),n)\approx\frac(1)(\sqrt(2\pi))\int\limits_(x")^(x"")e^(-x^2/2) \, dx,де.

При вирішенні завдань, які потребують застосування інтегральної теореми Лапласа, користуються спеціальними таблицями, оскільки невизначений інтеграл \int(e^(-x^2/2)\,dx)не виражається через елементарні функції. Таблиця для інтегралу \Phi(x)=\frac(1)(\sqrt(2\pi))\int\limits_(0)^(x)e^(-z^2/2)\,dzнаведено у дод. 2 де дані значення функції \Phi(x) для позитивних значень x , для x<0 используют ту же таблицу (функция \Phi(x) нечетна, т. е. \Phi(-x)=-\Phi(x) ). Таблица содержит значения функции \Phi(x) лишь для x\in ; для x>5 можна прийняти \Phi(x)=0,\!5 .

Отже, приблизно ймовірність того, що подія A з'явиться в n незалежних випробуваннях від m_1 до m_2 разів,

P_((m_1,m_2),n)\approx\Phi(x"")-\Phi(x"),де x"=\frac(m_1-np)(\sqrt(npq)); ~x""=\frac(m_2-np)(\sqrt(npq)).

Приклад 4. Імовірність того, що деталь виготовлена ​​з порушеннями стандартів p=0,!2 . Знайти ймовірність того, що серед 400 випадково відібраних нестандартних деталей виявиться від 70 до 100 деталей.

Рішення. За умовою p=0,\!2,\,q=0,\!8,\,n=400,\,m_1=70,\,m_2=100. Скористаємося інтегральною теоремою Лапласа:

P_((70,100),400)\approxPhi(x"")-Phi(x").

Обчислимо межі інтегрування:

нижній

X"=\frac(m_1-np)(\sqrt(npq))=\frac(70-400\cdot0,\!2)(\sqrt(400\cdot0,\!2\cdot0,\!8)) =-1, \! 25,

верхній

X""=\frac(m_2-np)(\sqrt(npq))=\frac(100-400\cdot0,\!2)(\sqrt(400\cdot0,\!2\cdot0,\!8) ) = 2, \! 5,

Таким чином

P_((70,100),400)\approx\Phi(2,\!5)-\Phi(-1,\!25)=\Phi(2,\!5)+\Phi(1,\!25) .

За таблицею дод. 2 знаходимо

\Phi(2,\!5)=0,\!4938;~~~~~\Phi(1,\!25)=0,\!3944.

Шукана ймовірність

P_((70,100),400) = 0, 4938 +0, 3944 = 0, 8882.

Застосування інтегральної теореми Лапласа

Якщо число m (кількість події A при n незалежних випробуваннях) буде змінюватися від m_1 до m_2 , то дріб \frac(m-np)(\sqrt(npq))буде змінюватися від \frac(m_1-np)(\sqrt(npq))=x"до \frac(m_2-np)(\sqrt(npq))=x"". Отже, інтегральну теорему Лапласа можна записати і так:

P\left\(x"\leqslant\frac(m-np)(\sqrt(npq))\leqslant(x"")\right\)=\frac(1)(\sqrt(2\pi))\ int\limits_(x")^(x"")e^(-x^2/2)\,dx.

Поставимо завдання знайти ймовірність того, що відхилення відносної частоти \frac(m)(n) від постійної ймовірності p по абсолютної величинине перевищує заданого числа \varepsilon>0. Іншими словами, знайдемо ймовірність здійснення нерівності \left|\frac(m)(n)-p\right|\leqslant\varepsilon, що те саме, -\varepsilon\leqslant\frac(m)(n)-p\leqslant\varepsilon. Цю ймовірність будемо позначати так: P\left\(\left|\frac(m)(n)-p\right|\leqslant\varepsilon\right\). З урахуванням формули (3.6) для цієї ймовірності отримуємо

P\left\(\left|\frac(m)(n)-p\right|\leqslant\varepsilon\right\)\approx2\Phi\left(\varepsilon\,\sqrt(\frac(n)(pq) )) \ right).

Приклад 5. Імовірність того, що деталь нестандартна, p = 0, 1! Знайти ймовірність того, що серед випадково відібраних 400 деталей відносна частота появи нестандартних деталей відхилиться від ймовірності p = 0, 1 по абсолютній величині не більше ніж на 0,03.

Рішення. За умовою n=400,\,p=0,\!1,\,q=0,\!9,\,\varepsilon=0,\!03. Потрібно знайти ймовірність P\left\(\left|\frac(m)(400)-0,\!1\right|\leqslant0,\!03\right\). Використовуючи формулу (3.7), отримуємо

P\left\(\left|\frac(m)(400)-0,\!1\right|\leqslant0,\!03\right\)\approx2\Phi\left(0,\!03\sqrt( \frac(400)(0,\!1\cdot0,\!9))\right)=2\Phi(2)

За таблицею дод. 2 знаходимо \Phi(2)=0,\!4772 , отже, 2\Phi(2)=0,\!9544 . Отже, шукана ймовірність приблизно дорівнює 0,9544. Сенс отриманого результату такий: якщо взяти досить велике число проб по 400 деталей у кожній, то приблизно 95,44% цих проб відхилення відносної частоти від постійної ймовірності p=0,!1 по абсолютній величині не перевищить 0,03.

Формула Пуассона для малоймовірних подій

Якщо ймовірність настання події в окремому випробуванні близька до нуля, то навіть при великому числівипробувань n, але при невеликому значенні твори np одержувані за формулою Лапласа значення ймовірностей P_(m,n) виявляються недостатньо точними і виникає потреба в іншій наближеній формулі.

Теорема 3.3. Якщо ймовірність p настання події A у кожному випробуванні постійна, але мала, число незалежних випробувань n досить велике, але значення твору np=\lambda залишається невеликим (не більше десяти), то ймовірність того, що в цих випробуваннях подія A настане m разів,

P_(m,n)\approx\frac(\lambda^m)(m\,e^{-\lambda}. !}

Для спрощення розрахунків із застосуванням формули Пуассона складено таблицю значень функції Пуассона \frac(\lambda^m)(m\,e^{-\lambda} !}(Див. дод. 3).

Приклад 6. Нехай можливість виготовлення нестандартної деталі дорівнює 0,004. Знайти ймовірність того, що серед 1000 деталей виявиться 5 нестандартних.

Рішення. Тут n=1000,p=0,004,~\lambda=np=1000\cdot0,\!004=4. Усі три числа задовольняють вимогам теореми 3.3, тому знаходження ймовірності шуканої події P_(5,1000) застосовуємо формулу Пуассона. За таблицею значень функції Пуассона (додаток 3) при \lambda=4;m=5 отримуємо P_(5,1000)\approx0,\!1563.

Знайдемо ймовірність тієї самої події за формулою Лапласа. Для цього спочатку обчислюємо значення x відповідне m=5 :

X=\frac(5-1000\cdot0,\!004)(\sqrt(1000\cdot0,\!004\cdot0,\!996))\approx\frac(1)(1,\!996)\approx0 , \!501.

Тому згідно з формулою Лапласа шукана ймовірність

P_(5,1000)\approx\frac(\varphi(0,\!501))(1,\!996)\approx\frac(0,\!3519)(1,\!996)\approx0,\ !1763

а згідно з формулою Бернуллі точне її значення

P_(5,1000)=C_(1000)^(5)\cdot0,\!004^5\cdot0,\!996^(995)\approx0,\!1552.

Таким чином, відносна помилкаобчислення ймовірностей P_(5,1000) за наближеною формулою Лапласа складає

\frac(0,\!1763-0,\!1552)(0,\!1552)\approx0,\!196, або 13, 6%

а за формулою Пуассона -

\frac(0,\!1563-0,\!1552)(0,\!1552)\approx0,\!007, або 0, 7%

Т. е. у багато разів менше.
Перейти до наступного розділу
Одновимірні випадкові величини У вашому браузері вимкнено Javascript.
Щоб розрахувати, необхідно дозволити елементи ActiveX!

1

1. Боголюбов О.М. Математики. Механіки: біографічний довідник - Київ: Наукова думка, 1983.

2. Гулай Т.А., Долгополова О.Ф., Литвин Д.Б. Аналіз та оцінка пріоритетності розділів математичних дисциплін, що вивчаються студентами економічних спеціальностей аграрних вузів // Вісник АПК Ставропілля. - 2013. - № 1 (9). - С. 6-10.

3. Долгополова А.Ф., Гулай Т.А., Литвин Д.Б. Перспективи застосування математичних методівв економічних дослідженнях / / Аграрна наука, творчість, зростання. - 2013. - С. 255-257.

У математиці часто зустрічаються завдання, у яких присутня велика кількість повторень однієї й тієї ж умови, випробування чи експерименту. Результатом кожного випробування буде вважатися зовсім інший результат від попереднього. Залежності в результатах також спостерігатися не буде. Як результат випробування можна розрізнити кілька можливостей елементарних наслідків: виникнення події (А) або виникнення події, яке доповнює А.

Тоді спробуємо припустити, що можливість виникнення події Р(А) регулярна і дорівнює р (0<р<1).

Прикладами такого випробування може бути велика кількість завдань, таких як підкидання монетки, вилучення з темного мішка чорно-білих куль або народження чорно-білих кроликів.

Такий експеримент називають конфігурацією повторних незалежних випробувань чи схемою Бернуллі.

Якоб Бернуллі народився у сім'ї фармацевта. Батько намагався наставити сина на медичний шлях, але Я. Бернуллі захопився математикою самостійно, а пізніше це стало його професією. Йому належать різні трофеї у роботах на теми з теорії ймовірностей та чисел, рядів та диференціального числення. Вивчивши теорію ймовірності з однієї роботи Гюйгенса «Про розрахунки в азартній грі», Якоб захопився цим. У цій книзі був навіть чіткого визначення концепції «імовірність». Саме Я. Бернуллі ввів у математику більшу частину сучасних понять теорії ймовірностей. Так само Бернуллі першим висловив свій варіант закону великих чисел. Ім'я Якоба носять різні роботи, теореми та схеми: «Числа Бернуллі», «Многочлен Бернуллі», «Диференційне рівняння Бернуллі», «Розподіл Бернуллі» та «Рівняння Бернуллі».

Повернемося до повторень. Як було зазначено вище, то результаті різних випробувань можливі два результати: або з'явиться подія А, або протилежність цієї події. Сама схема Бернуллі позначає виробництво n-го кількості типових вільних дослідів, і в кожному з цих дослідів може з'явитися необхідна подія А (ймовірність цієї події відома: Р(А)=р), ймовірність протилежної події події А позначена за q=P( A) = 1-p. Потрібно визначення ймовірності, що з проведенні випробувань невідомої кількості подія А з'явиться рівно k раз.

Важливо пам'ятати про основну умову при вирішенні завдань за допомогою схеми Бернуллі-це сталість. Без нього схема втрачає будь-який сенс.

Цією схемою можна використовувати рішення завдань різного рівня складності: від простих (та сама монетка) до складних (відсотки). Однак найчастіше схема Бернуллі застосовується у вирішенні таких завдань, які пов'язані з контролем властивостей різної продукції та впевненості в різних механізмах. Тільки для вирішення завдання до початку роботи повинні бути відомі заздалегідь всі умови та значення.

Не всі завдання теорії ймовірностей зводяться до сталості за умов. Навіть якщо взяти за приклад чорні та білі кулі у темному мішку: при витягуванні однієї кулі співвідношення кількості та кольорів кульок у мішку змінилося, а значить змінилася і сама ймовірність.

Однак якщо ж умови у нас постійні, то ми можемо точно визначити необхідну від нас ймовірність того, що подія А відбудеться рівно з n можливих.

Цей факт Якоб Бернуллі скомпонував теорему, яку згодом стали називати його ім'ям. "Теорема Бернуллі" є однією з головних теорем у теорії ймовірності. Вперше її опублікували у праці Я.Бернуллі «Мистецтво припущень». Що ж є ця теорема? «Якщо ймовірність р наступу події А кожному випробуванні постійна, то ймовірність Рk,n те, що подія настане k разів у n випробуваннях, які залежать друг від друга дорівнює: , де q=1-p».

На підтвердження дієвості формули можна навести завдання.

Завдання № 1:

З n скляних банок протягом місяця зберігання k розбиваються. Навмання взяли m банок. Знайти ймовірність, що серед цих банок не розіб'ються. n=250, k=10, m=8,l=4.

Рішення: Маємо схему Бернуллі зі значеннями:

p=10/250=0,04 (імовірність те, що банки розіб'ються);

n=8 (кількість випробувань);

k=8-4=4 (кількість розбитих банок).

Використовуємо формулу Бернуллі

Отримали:

Відповідь: 0,0141

Завдання № 2:

Імовірність виготовлення несправного виробу з виробництва дорівнює 0,2. Знайти ймовірність того, що з 10 виготовлених на цьому виробництві виробів рівно k повинні бути справними. Виконати рішення k = 0, 1, 10.

Нам цікава подія A - виготовлення справних деталей, що відбувається раз на годину з ймовірністю p=1-0,2=0,8. Потрібно визначити ймовірність того, що ця подія відбудеться до разів. Події A протилежна подія «не A», тобто. Виготовлення несправного виробу.

Отже, маємо: n=10; p=0,8; q=0,2.

У результаті знайдемо можливість, що з 10 виготовлених виробів всі вироби несправні (k=0), що один виріб справний (k=1), що несправних немає взагалі (k=10):

У висновку хотілося б відзначити, що в сучасності багато вчених намагаються довести, що «формула Бернуллі» не відповідає законам природи і можна вирішити завдання, не застосовуючи її до використання. Звичайно, це можливо, більшість завдань з теорії ймовірності можливо виконати без формули Бернуллі, головне не заплутатися у великих обсягах цифр.

Бібліографічне посилання

Хомутова Є.А., Калініченко В.А. ФОРМУЛА БЕРНУЛИ В ТЕОРІЇ МОЖЛИВОСТІ // Міжнародний студентський науковий вісник. - 2015. - № 3-4.;
URL: http://eduherald.ru/ru/article/view?id=14141 (дата звернення: 12.03.2019). Пропонуємо до вашої уваги журнали, що видаються у видавництві «Академія Природознавства»