Төрөл бүрийн байршлын тоо. Комбинаторикийн үндсэн томъёо. Комбинаторик: орлуулах томъёо, байрлуулах

Дахин зохицуулалт. Сэлгээний тооны томъёо

-аас солих n элементүүд

Багцыг нь тавь Xорно n элементүүд.

Тодорхойлолт. -аас давталгүйгээр байршуулахn багцын элементүүдX By n дуудсан -аас солих n элементүүд.

Аливаа сэлгэлт нь олонлогийн бүх элементүүдийг агуулна гэдгийг анхаарна ууX , мөн яг нэг удаа. Өөрөөр хэлбэл, сэлгэлт нь зөвхөн элементүүдийн дарааллаар бие биенээсээ ялгаатай бөгөөд элементүүдийг солих замаар бие биенээсээ олж авч болно (иймээс нэр).

Бүх сэлгэцийн тооn элементүүдийг тэмдгээр тэмдэглэв .

Нэгэнт сэлгэлт байдаг онцгой тохиолдолдээр давталтгүйгээр байршуулах , дараа нь тоог олох томъёо Бид үүнийг (2) томъёогоор орлуулж авна :

Тиймээс,

(3)

Жишээ. 5 номыг тавиур дээр хэдэн янзаар байрлуулж болох вэ?

Шийдэл. Номыг тавиур дээр байрлуулах олон арга байдаг тул таван элементийн өөр өөр орлуулалт байдаг:арга замууд.

Сэтгэгдэл. (1)-(3) томъёог цээжлэх шаардлагагүй: тэдгээрийн хэрэглээтэй холбоотой асуудлыг бүтээгдэхүүний дүрмийг ашиглан үргэлж шийдэж болно. Хэрэв оюутнуудад бодлогын хослолын загварыг бий болгоход бэрхшээлтэй байгаа бол ашигласан томъёо, дүрмийн багцыг нарийсгах нь дээр (алдаа гаргах боломж бага байх болно). Оршил, томъёо (3)-ыг ашигладаг асуудлуудыг ихэвчлэн ямар ч асуудалгүйгээр шийддэг нь үнэн.

Даалгаврууд

1. F. Тэд билетийн касс дээр хэдэн янзаар дараалал үүсгэж болох вэ: 1) 3 хүн; 2) 5 хүн?

Шийдэл.

Төрөл бүрийн сонголтуудДараалалд байгаа n хүний ​​зохион байгуулалт нь зөвхөн хүмүүсийн байрлалын дарааллаар бие биенээсээ ялгаатай, өөрөөр хэлбэл тэдгээр нь n элементийн өөр өөр солигдол юм.

Гурван хүн P3 = 3 дараалалд орж болно! = 6 өөр арга.

Хариулт: 1) 6 арга; 2) 120 арга.

2. T. Дөрвөн хүний ​​суудалтай вандан сандал дээр 4 хүн хэдэн янзаар багтах вэ?

Шийдэл.

Хүмүүсийн тоо нь вандан сандал дээрх суудлын тоотой тэнцүү тул байрлуулах сонголтуудын тоо нь 4 элементийн сэлгэцийн тоотой тэнцүү байна: P4 = 4! = 24.

Та бүтээгдэхүүний дүрмийн дагуу дүгнэлт хийж болно: эхний хүнд 4 газрын аль нэгийг сонгох боломжтой, хоёр дахь нь - үлдсэн 3-ын аль нэгийг, гурав дахь нь - үлдсэн 2-ын аль нэгийг нь сонгох боломжтой, сүүлийн нэг нь үлдсэн 1 байрыг авна. ; бүх зүйл бий = Дөрвөн хүний ​​суудалтай вандан сандал дээр 4 хүнийг суулгах 24 өөр арга.

Хариулт: 24 арга.

3. M. At Vova’s үдийн хоолонд - нэгдүгээр, хоёрдугаар, гуравдугаар курс, бялуу. Тэр мэдээж бялуугаар эхэлж, үлдсэнийг нь идэх болно тодорхой дарааллаар. Дугаарыг нь олоорой боломжит сонголтуудүдийн хоол.

Сурах бичгээс М-бодлого. А.Г. Мордковичийн гарын авлага

Т - ред. С.А.Теляковский

Ф- М.В.Ткачева

Шийдэл.

Бялууны дараа Вова гурван тавагны аль нэгийг нь сонгож, дараа нь хоёрыг нь сонгож, үлдсэнийг нь дуусгаж болно. Үдийн хоолны боломжит сонголтуудын нийт тоо: =6.

Хариулт: 6.

4. F. Өгүүлбэр дэх үгсийн дарааллыг өөрчилснөөр хэдэн өөр зөв (орос хэлний үүднээс) хэллэг зохиож болох вэ: 1) "Би зугаалахаар явсан"; 2) "Муур хашаанд алхаж байна"?

Шийдэл.

Хоёрдахь өгүүлбэрт "in" гэсэн угтвар үг нь хамаарах "yard" гэсэн нэр үгийн өмнө заавал байх ёстой. Тиймээс, "хашаанд" гэсэн хосыг нэг үгээр тоолбол та гурван нөхцөлт үгийн өөр өөр орлуулах тоог олох боломжтой: P3 = 3! = 6. Тиймээс энэ тохиолдолд та 6 зөв өгүүлбэр хийж болно.

Хариулт: 1) 6; 2) 6.

5. Дөрвөн өнцөгтийн оройг тодорхойлохын тулд K, L, M, H үсгийг хэдэн янзаар ашиглаж болох вэ?

Шийдэл.

Дөрвөн өнцөгтийн оройнуудыг дугаарласан, тус бүр нь тогтмол тоотой гэж бид таамаглах болно. Дараа нь асуудал нь 4 үсгийг 4 газар (орой) байрлуулах янз бүрийн аргын тоог тоолох, өөрөөр хэлбэл өөр өөр орлуулах тоог тоолох явдал юм: P4 = 4! =24 арга.

Хариулт: 24 арга.

6. F. Дөрвөн найз кино театрын тасалбар худалдаж авсан: нэгдүгээр эгнээний 1, 2-р суудал, хоёр дахь эгнээний 1, 2-р суудал. Найзууд кино театрын эдгээр 4 суудлыг хэдэн янзаар авч болох вэ?

Шийдэл.

Дөрвөн найз 4 өөр газар авах боломжтой P4 = 4! = 24 өөр арга.

Хариулт: 24 арга.

7. T. Илгээгч нь багцыг 7 өөр байгууллагад хүргэх ёстой. Тэр хэдэн замыг сонгож чадах вэ?

Шийдэл.

Маршрутыг шуудан зөөгч байгууллагуудад очих дараалал гэж ойлгох хэрэгтэй. Байгууллагуудыг 1-ээс 7 хүртэл дугаарлая, дараа нь маршрутыг 7 тооны дарааллаар харуулах бөгөөд тэдгээрийн дараалал өөрчлөгдөж болно. Маршрутын тоо нь 7 элементийн сэлгэцийн тоотой тэнцүү байна: P7= 7! = 5,040.

Хариулт: 5040 маршрут.

8. T. Хүчин зүйлүүдийг дахин цэгцэлж түүнээс гаргаж авсан abcde үржвэртэй ижил тэнцүү хэдэн илэрхийлэл байдаг вэ?

Шийдэл.

Дараалал нь өөрчлөгдөж болох abcde таван өөр хүчин зүйлийн үржвэрийг өгсөн болно (хүчин зүйлүүдийг дахин зохион байгуулахад бүтээгдэхүүн өөрчлөгдөхгүй).

Нийт P5 = 5 байна! = Таван үржүүлэгчийг зохион байгуулах 120 өөр арга; Бид тэдгээрийн аль нэгийг нь (abcde) анхных гэж үздэг, үлдсэн 119 илэрхийлэл нь үүнтэй ижил байна.

Хариулт: 119 илэрхийлэл.

9. Т.Ольга найзынхаа утасны дугаар 5, 7, 8 гэсэн тоогоор төгссөнийг санаж байгаа ч эдгээр дугаарууд ямар дарааллаар гарч ирдгийг мартжээ. Найзтайгаа уулзахын тулд түүний хийх ёстой хамгийн олон сонголтыг зааж өгнө үү.

Шийдэл.

Утасны дугаарын сүүлийн гурван орон нь P3 =3-ын аль нэгэнд байрлаж болно! =6 боломжит захиалга, үүнээс зөвхөн нэг нь зөв. Ольга тэр даруй залгаж болно зөв сонголт, гуравдугаарт залгаж болно гэх мэт. Тэр хамгийн олон тооны сонголтуудыг залгах шаардлагатай болно зөв сонголтсүүлчийнх, өөрөөр хэлбэл зургаа дахь нь байх болно.

Хариулт: 6 сонголт.

10. T. Тооноос хэдэн зургаан оронтой тоо (давтаагүй тоо) хийж болох вэ: a) 1,2, 5, 6, 7, 8; б) 0, 2, 5, 6, 7, 8? Шийдэл.

a) Өгөгдсөн 6 оронтой: 1, 2, 5, 6, 7, 8, тэдгээрээс та зөвхөн эдгээр цифрүүдийг дахин цэгцлэх замаар өөр өөр зургаан оронтой тоо гаргаж болно. Өөр өөр зургаан оронтой тооны тоо P6 = 6-тай тэнцүү байна! = 720.

б) Өгөгдсөн 6 оронтой тоо: 0, 2, 5, 6, 7, 8, тэдгээрээс та янз бүрийн зургаан оронтой тоо гаргах хэрэгтэй. Өмнөх асуудлаас ялгагдах зүйл нь тэг нь эхэлж болохгүй.

Та бүтээгдэхүүний дүрмийг шууд хэрэглэж болно: эхний байранд 5 цифрээс (тэгээс бусад) аль нэгийг нь сонгож болно; хоёрдугаарт - үлдсэн 5 цифрийн аль нэг нь (4 нь "тэг биш" бөгөөд одоо бид тэгийг тоолж байна); Гуравдугаар байранд - эхний хоёр сонголтын дараа үлдсэн 4 цифрийн аль нэг нь гэх мэт. Нийт сонголтуудын тоо: = 600.

Та шаардлагагүй сонголтуудыг арилгах аргыг ашиглаж болно. 6 цифрийг P6 = 6 болгон өөрчилж болно! = 720 өөр арга зам. Эдгээр аргуудын дунд эхний ээлжинд тэг байх аргууд байх болно, энэ нь хүлээн зөвшөөрөгдөхгүй юм. Эдгээр хүчингүй сонголтуудын тоог тоолъё. Хэрэв эхний ээлжинд тэг байгаа бол (энэ нь тогтмол), дараа нь дараагийн таван байранд "тэг бус" 2, 5, 6, 7, 8 гэсэн 5 тоо байх янз бүрийн аргын тоог агуулж болно 5 газар байрлуулж болно P5 = 5 тэнцүү! = 120, өөрөөр хэлбэл тэгээс эхэлсэн тоонуудын орлуулах тоо нь 120. Энэ тохиолдолд өөр өөр зургаан оронтой тоонуудын шаардлагатай тоо нь тэнцүү байна: P6 - P5 = 720 - 120 = 600.

Хариулт: a) 720; б) 600 тоо.

11. T. Хэр их дунд дөрвөн оронтой тоо(дахин давтагдахгүйгээр) 3, 5, 7, 9 гэсэн тооноос бүрдэнэ: а) 3-аар эхэлсэн;

б) 15-ын үржвэр үү?

Шийдэл.

a) 3, 5, 7, 9 тоонуудаас бид 3-аас эхэлсэн дөрвөн оронтой тоог гаргадаг.

Бид эхний ээлжинд 3 дугаарыг засдаг; дараа нь үлдсэн гурав дээр5, 7 9 тоонуудыг дурын дарааллаар байрлуулж болно. Тэдний байршлын сонголтуудын нийт тоо P-тэй тэнцүү байна 3 = 3!=6. Дөрвөн оронтой тооноос бүрдэх маш олон янзын тоо байх болноөгөгдсөн тоонууд ба 3-аас эхэлнэ.

б) Эдгээр цифрүүдийн нийлбэр 3 + 5 + 7 + 9 = 24 нь 3-т хуваагддаг тул эдгээр цифрүүдээс бүрдсэн дөрвөн оронтой тоо 3-т хуваагддаг болохыг анхаарна уу. Эдгээр тоонуудын зарим нь хуваагддаг байхын тулд 15 гэхэд 5-аар төгсөх шаардлагатай.

Бид 5-ын тоог хамгийн сүүлд засдаг; үлдсэн 3 цифрийг 5 Rz = 3-ын урд гурван газар байрлуулж болно! = 6 өөр арга. 15-д хуваагдах эдгээр тооноос бүрдэх маш олон янзын дөрвөн оронтой тоо байх болно.

Хариулт: a) 6 тоо; б) 6 тоо.

12. T. 1, 3, 5, 7 тоонуудаас гаргаж болох дөрвөн оронтой бүх тооны цифрүүдийн нийлбэрийг ол (давталгүйгээр).

Шийдэл.

1, 3, 5, 7 (давталтгүйгээр) цифрүүдээс бүрдэх дөрвөн оронтой тоо бүр 1 + 3 + 5 + 7 = 16-тай тэнцүү цифрүүдийн нийлбэртэй байна.

Эдгээр тооноос та P4 = 4 болгож чадна! = 24 өөр өөр тоо, зөвхөн цифрүүдийн дарааллаар ялгаатай. Эдгээр бүх тооны цифрүүдийн нийлбэр нь тэнцүү байх болно

16 = 384.

Хариулт: 384.

13. Т.Олег, Игорь нарын долоон хөвгүүн дараалан зогсож байна. Дараах тохиолдолд боломжит хослолын тоог ол.

a) Олег эгнээний төгсгөлд байх ёстой;

б) Олег эгнээний эхэнд, Игорь эгнээний төгсгөлд байх ёстой;

в) Олег, Игорь нар бие биенийхээ хажууд зогсох ёстой.
Шийдэл.

a) 7 газарт ердөө 7 хөвгүүд байдаг, гэхдээ нэг элемент нь тогтмол бөгөөд дахин зохион байгуулах боломжгүй (Олег эгнээний төгсгөлд байна). Боломжит хослолын тоо нь Олегийн өмнө зогсож буй 6 хөвгүүдийн сэлгэцийн тоотой тэнцүү байна: P6=6!=720.

бусад таван элементтэй дахин нэг элемент болгон хослуулах. Дараа нь боломжит хослолуудын тоо P6 = 6 болно! = 720.

Одоо Олег, Игорь хоёрыг IO дарааллаар зэрэгцүүлэн зогсооцгооё. Дараа нь бид өөр P6 = 6 авна! = 720 өөр хослол.

Олег, Игорь хоёр бие биенийхээ хажууд байгаа хослолын нийт тоо (ямар ч дарааллаар) 720 + 720 = 1,440 байна.

Хариулт: a) 720; б) 120; в) 1440 хослол.

14. M. Тоглолт эхлэхийн өмнө арван нэгэн хөлбөмбөгчин жагсаж байна. Эхнийх нь ахлагч, хоёр дахь нь хаалгач, бусад нь санамсаргүй байдлаар ажилладаг. Барилгын хэдэн арга байдаг вэ?

Шийдэл.

Ахлагч, хаалгачийн дараа гурав дахь тоглогч үлдсэн 9 газрын аль нэгийг, 8-аас дараагийнх гэх мэтийг сонгож болно. Бүтээгдэхүүний дүрмийг ашигласан барилгын аргын нийт тоо нь:

1 =362,880, эсвэл P 9 = 9! = 362,880.

Хариулт: 362,880.

15. M. Кубын оройг A, B, C, D, E, F, G, K үсгээр хэдэн янзаар тэмдэглэж болох вэ?

Шийдэл.

Эхний оройн хувьд та 8 үсгийн аль нэгийг, хоёр дахь нь - үлдсэн 7 үсгийн аль нэгийг сонгож болно. Бүтээгдэхүүний дүрмийн дагуу нийт аргын тоо байна.=40 320, эсвэл P8 = 8!

Хариулт: 40,320.

16. T. Даваа гарагийн хуваарь нь алгебр, геометр, биологи, түүх, биеийн тамир, хими гэсэн зургаан хичээлтэй. Та энэ өдрийн хичээлийн хуваарийг хэд хэдэн аргаар зохиож, хоёр математикийн хичээлийг зэрэгцүүлж болох вэ?

Шийдэл.

Нийт 6 хичээлтэй, үүнээс хоёр математикийн хичээл хажууд байх ёстой.

Бид хоёр элементийг (алгебр ба геометр) эхлээд AG дарааллаар, дараа нь GA дарааллаар "наав". "Наах" сонголт бүрийн хувьд бид P5 = 5 авна! = 120 хуваарийн сонголт. Хуваарь үүсгэх арга замын нийт тоо нь 120 (AG) +120 (GA) = 240 байна.

Хариулт: 240 арга.

17. T. “Конус” гэдэг үгийн K, O, N үсэг зэрэгцэн оршдог үсгүүдийн хэдэн солих вэ?

Шийдэл.

5 үсэг өгөгдсөн бөгөөд тэдгээрийн гурав нь бие биенийхээ хажууд байх ёстой. K, O, N гурван үсэг P3 = 3-ын аль нэгнийх нь хажууд зогсож болно! = 6 арга. K, O, N үсгүүдийг "наах" арга бүрийн хувьд бид P3 = 3 авна! = Үсгийг солих 6 арга, "наах", U, S. K, O, N үсэг зэрэгцэн оршдог "конус" үгийн үсгүүдийн өөр өөр солилтын нийт тоо 6 6 = 36 байна. пермутаци - анаграмууд.

Хариулт: 36 анаграмм.

18. Т.Театрын нэг эгнээнд 5 хүү, 5 охин 1-ээс 10 хүртэлх суудалд хэдэн янзаар суух вэ? Хөвгүүд сондгой тоотой, охид тэгш тоотой суудалд суувал тэд үүнийг хэдэн аргаар хийж чадах вэ?

Шийдэл.

Хөвгүүдийн зохион байгуулалт бүрийг охидын зохион байгуулалттай хослуулж болно, тиймээс бүтээгдэхүүний дүрмийн дагуу нийт тооЭнэ тохиолдолд хүүхдийг суулгах 120 арга бий. 20= 14400.

Хариулт: 3,628,800 арга зам; 14,400 арга зам.

19. Т.Таван хөвгүүн, дөрвөн охин есөн хүний ​​суудалтай сандал дээр суухыг хүсдэг бөгөөд ингэснээр охин бүр хоёр хөвгүүний дунд сууна. Тэд үүнийг хэдэн аргаар хийж чадах вэ?

Шийдэл.

Даалгаврын нөхцлийн дагуу охид, хөвгүүд ээлжлэн солигдох ёстой, өөрөөр хэлбэл охид зөвхөн тэгш тоотой, хөвгүүд зөвхөн сондгой тоотой газар сууж болно. Тиймээс охид зөвхөн охидтой, хөвгүүд зөвхөн хөвгүүдтэй байраа сольж болно. Дөрвөн охин дөрвөн тэгш газар P4 = 4 сууж болно! = 24 арга, таван сондгой газар таван хөвгүүн P5 = 5! = 120 арга.

Охидыг байрлуулах арга бүрийг хөвгүүдийг байрлуулах арга бүртэй хослуулж болох тул бүтээгдэхүүний дүрмийн дагуу нийт аргын тоо дараах байдалтай тэнцүү байна: P420 = 2880 арга.

Хариулт: 2880 арга.

20. F. 30 ба 210 тоонуудыг энгийн үржвэрийн үржвэр болгон хэдэн аргаар бичиж болох вэ: 1) 30; 2) 210?

Шийдэл.

Эдгээр тоонуудыг анхны хүчин зүйл болгон авч үзье.

30 = 2 ; 210 = 2 .

30-ын тоог анхны хүчин зүйлийн үржвэр болгон бичиж болно

Р 3 = 3! = 6 янз бүрийн арга замууд(хүчин зүйлүүдийг дахин цэгцлэх).

210 тоог анхны тоонуудын үржвэр болгон бичиж болно
үржүүлэгчидР 4 = 4! = 24 өөр арга.

Хариулт: 1) 6 арга; 2) 24 арга.

21. F. 1, 2, 3, 5 тоонуудыг ашиглан давтагдахгүй цифрүүдтэй хэдэн өөр тэгш дөрвөн оронтой тоог бичиж болох вэ?

Шийдэл.

Тоо тэгш байхын тулд тэгш оронтой тоогоор төгссөн байх ёстой, өөрөөр хэлбэл 2. Хоёрыг сүүлчийн байранд нь засъя, үлдсэн гурван орон нь урд нь дурын дарааллаар гарч ирэх ёстой. 3 оронтой өөр өөр орлуулалтын тоо P3 = 3 байна! = 6; тиймээс бас 6 өөр тэгш дөрвөн оронтой тоо байх болно (гурван оронтой солих бүрт 2-ын тоог нэмнэ).

Хариулт: 6 тоо.

22. F. 1,2, 4, 6, 8 оронтой тоогоор ижил оронгүй хэдэн өөр сондгой таван оронтой тоог бичиж болох вэ?

Шийдэл.

Бүрдсэн тоо сондгой байхын тулд сондгой тоогоор төгссөн байх ёстой, өөрөөр хэлбэл нэг. Үлдсэн 4 цифрийг нэгжийн өмнө байрлуулж, дахин цэгцэлж болно.

Таван оронтой сондгой тооны нийт тоо нь солих тоотой тэнцүү байна: P4 = 4! =24.

23. F. 1-ийн цифрийг ашиглан дахин давтагдахгүй цифртэй хэдэн өөр зургаан оронтой тоог бичиж болох вэ? 2 3, 4, 5, 6, хэрэв: 1) тоо нь 56-аар эхлэх ёстой; 2) 5 ба 6 тоонууд хажууд байх ёстой юу?

Шийдэл.

Бид тооны эхэнд 5 ба 6 гэсэн хоёр цифрийг засаж, үлдсэн 4 цифрээс янз бүрийн орлуулалтуудыг нэмнэ; өөр өөр зургаан оронтой тооны тоо тэнцүү байна: P4 = 4! = 24.

5 ба 6-ын цифрүүд (ямар ч дарааллаар) байгаа өөр өөр зургаан оронтой тоонуудын нийт тоо нь 120 + 120 = 240 тоо юм. (56 ба 65-р сонголтууд нь хоорондоо нийцэхгүй тул нэгэн зэрэг хэрэгжүүлэх боломжгүй; бид нэгтгэлийн нийлбэр дүрмийг хэрэгжүүлдэг.)

Хариулт: 1) 24 дэх; 2) 240 тоо.

24. F. 1,2,3,4 тоонуудаас ижил цифргүй хэдэн өөр тэгш дөрвөн оронтой тоо гаргаж болох вэ?

Шийдэл.

Тэгш тоо тэгш оронтой тоогоор төгсөх ёстой. Бид 2-ын тоог хамгийн сүүлд засаж, дараа нь өмнөх 3 цифрийг P3 = 3 болгон өөрчилж болно! = 6 өөр арга; Бид төгсгөлд нь хоёртой 6 тоог авна. Бид 4-ийн тоог хамгийн сүүлд засаж, бид P3 = 3 авна! = Өмнөх гурван цифр болон 4-өөр төгссөн 6 тооны өөр өөр 6 тооны солилт.

Тэгш дөрвөн оронтой тооны нийт тоо нь 6 + 6 = 12 өөр тоо байх болно.

Хариулт: 12 тоо.

Сэтгэгдэл. Бид хослолын нийлбэрийн дүрмийг ашиглан нийт сонголтуудын тоог олдог (хоёроор төгссөн тоонуудын 6 сонголт, дөрөвөөр төгссөн тоонуудын 6 сонголт; төгсгөлд нь хоёр ба дөрөвтэй тоо барих аргууд нь бие биенээ үгүйсгэдэг, хоорондоо нийцэхгүй байдаг. нийтсонголтууд нь төгсгөлд нь 2, төгсгөлд нь 4-тэй сонголтуудын тоонуудын нийлбэртэй тэнцүү). 6 + 6 = 12 гэсэн оруулга нь P оруулгатай харьцуулахад бидний үйлдлийн шалтгааныг илүү сайн тусгасан болно.

25. F. 1) 12 тоог анхны үржвэрийн үржвэр болгон хэдэн янзаар бичих вэ? 2) 24; 3) 120?

Шийдэл.

Энэ асуудлын онцлог нь эдгээр тоо тус бүрийн задралд ижил, давтагдах хүчин зүйлүүд байдаг. Хүчин зүйлсээс өөр өөр сэлгэлт үүсгэх үед бид хоёр ижил хүчин зүйлийг сольсон тохиолдолд шинэ сэлгэлт авахгүй.

1) 12 тоог гурван үндсэн хүчин зүйл болгон задалдаг бөгөөд тэдгээрийн хоёр нь ижил байна: 12 = .

Хэрэв бүх хүчин зүйлүүд өөр байсан бол тэдгээрийг P3 = 3 бүтээгдэхүүнд дахин зохион байгуулж болно! = 6 өөр арга. Эдгээр аргуудыг жагсаахын тулд бид хоёр хоёрыг нөхцөлт байдлаар "ялгаж", нэгийг нь онцлон тэмдэглэнэ: 12 = 2.

Дараа нь оршин суугчдад задрах 6 хувилбар боломжтой.

Гэвч үнэн хэрэгтээ тоонуудын доогуур зураас нь математикт ямар ч утгагүй тул энгийн тэмдэглэгээний үр дүнд үүссэн 6 орлуулалт дараах байдалтай байна.

өөрөөр хэлбэл, бид 6 биш, харин 3 өөр сэлгэлт авсан.

P x гэж тэмдэглэе гурван элемент, түүний дотор хоёр ижил элементийн шаардлагатай тооны сэлгэлт; тэгвэл бидний олж авсан үр дүнг дараах байдлаар бичиж болно: Рз = Р X Гэхдээ 2 нь хоёр элементийн өөр өөр сэлгэлтийн тоо, өөрөөр хэлбэл 2 == 2! = P 2, тиймээс P3, = P x P 2, иймээс P x = . (энэ нь давталттай сэлгэлтийн тооны томъёо юм).

Зөвхөн нэгдмэл бүтээгдэхүүний дүрэмд үндэслэн хүн өөрөөр тайлбарлаж болно.

Гурван хүчин зүйлийн бүтээгдэхүүнийг бий болгохын тулд эхлээд 3-р хүчин зүйлийн газрыг сонгох; үүнийг гурван аргын аль нэгээр хийж болно. Үүний дараа бид үлдсэн хоёр зайг хоёроор дүүргэнэ; Үүнийг 1 аргаар хийж болно. Бүтээгдэхүүний дүрмийн дагуу нийт аргын тоо: 3-1 =3., Р x =20.

Хоёрдахь арга. Таван хүчин зүйлийн үржвэрийг бүрдүүлэхдээ бид эхлээд тав (5 арга), дараа нь гурвын (4 арга) газрыг сонгож, үлдсэн 3 газрыг хоёроор (1 арга) дүүргэнэ; бүтээгдэхүүний дүрмийн дагуу 5 4 1 = 20.

Хариулт: 1) 3; 2) 4; 3) 20.

26. F. 3 нүдийг улаан, үлдсэн 3 нүдийг цагаан, хар эсвэл ногоон өнгөөр ​​будсан (тус бүр өөр өөрийн өнгөтэй) байхаар 6 нүдийг хэдэн аргаар будаж болох вэ?

Шийдэл.

6 элементийн сэлгэлт, тэдгээрийн гурав нь ижил байна:

Үгүй бол: цагаанаар будахын тулд та 6 нүдний аль нэгийг сонгож болно, хар - 5-аас, ногоон - 4-ээс; Үлдсэн гурван эсийг улаанаар будсан байна. Нийт аргын тоо: 6 5 4 1 = 120.

Хариулт: 120 арга.

27.Т. Явган хүн хойд зүгт нэг, баруун тийш гурван блок явах ёстой. Бүх боломжит явган хүний ​​замыг бичнэ үү.= 4.

Хариулт: 4 маршрут.

28. M. a) Дөрвөн ижил албан тушаалтны үүдэнд дөрвөн дэд захирлын нэр бүхий самбар өлгөх шаардлагатай. Үүнийг хэдэн аргаар хийж болох вэ?

б) 9 “А” ангид лхагва гаригт 5 хичээл орно: алгебр, геометр, биеийн тамир, орос хэл, Англи хэл. Та энэ өдрийн хуваарийн хэдэн сонголт үүсгэж болох вэ?

в) Дөрвөн хулгайч дөрвөн зүгт нэг нэгээр нь хэдэн янзаар тарааж чадах вэ?

г) Адъютант генералын тушаалын таван хувийг таван хороонд хүргүүлэх ёстой. Тэр захиалгын хуулбарыг хүргэх замыг хэдэн аргаар сонгож болох вэ?

Шийдэл.

a) Эхний тавагны хувьд та 4 шүүгээний аль нэгийг сонгож болно,
Хоёр дахь нь - үлдсэн гурвын аль нэг нь, гурав дахь нь - үлдсэн хоёрын аль нэг нь, дөрөв дэх нь - нэг нь үлдсэн; дүрмийн дагуу
бүтээгдэхүүн, арга замуудын нийт тоо: 4 3 2 1 = 24, эсвэл P4 = 4! = 24.= 120, эсвэл P5 = 5! = 120.

Хариулт: a) 24; б) 120; в) 24; г) 120.

Уран зохиол

Афанасьев В.В. Жишээ ба асуудлууд дахь магадлалын онол, - Ярославль: Ярославль улсын багшийн их сургууль, 1994 он.

Баврин I. I. Дээд математик: Багшийн их сургуулийн хими, математикийн чиглэлээр суралцаж буй оюутнуудад зориулсан сурах бичиг - 2-р хэвлэл, шинэчилсэн найруулга. - М.: Боловсрол, 1993 он.

Бунимович Е.А., Булычев В.А. Магадлал ба статистик. 5-9-р анги: Ерөнхий боловсролын гарын авлага боловсролын байгууллагууд, - М .: тоодог, 2005.

Виленкин Н. Я болон бусад. Алгебр ба математик шинжилгээ 10-р ангийн хувьд: Зааварбүхий сургууль, ангийн сурагчдад зориулсан гүнзгийрүүлсэн судалгааматематик. - М.: Боловсрол, 1992.

Виленкин Н. Я болон бусад. 11-р ангийн алгебр, математикийн шинжилгээ: Математикийн гүнзгийрүүлсэн сургалттай сургууль, ангийн сурагчдад зориулсан сурах бичиг - М.: Просвещение, 1990.

Глэйзер Г.И. Сургуулийн математикийн түүх: 9-10-р анги. Багш нарт зориулсан гарын авлага. - М.: Боловсрол 1983 он.

Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Математик 9: Алгебр. Функцүүд. Өгөгдлийн шинжилгээ - М.: Bustard, 2000.

Колягин болон бусад. Алгебр ба анализын эхлэл 11-р анги. Сургуулийн математик - 2002 - No4 - 43,44,46-р тал.

Люпшкас В.С. Математикийн нэмэлт хичээлүүд: магадлалын онол: 9-11-р ангийн сурах бичиг - М., 1991.

Макарычев Ю.Н., Миндюк Н.Г. Статистик ба магадлалын онолын элементүүд: 7-9-р ангийн сурагчдад зориулсан сурах бичиг - М.: Просвещение, 2005.

Мордкович А.Г., Семенов П.В. Алгебр ба анализын эхлэл, 10-р анги: Ерөнхий боловсролын байгууллагын сурах бичиг (профайлын түвшин) - М.: Мнемосина, 2005.

Ткачева М.В., Федорова Н.Е. Статистикийн элементүүд ба магадлал: 7-9-р ангийн сурагчдад зориулсан сурах бичиг - М.: Просвещение, 2005.

Комбинаторикийн хувьд тэд өгөгдсөн объектуудаас (элементүүд) тодорхой төрлийн хэдэн хослол хийж болох тухай асуултуудыг судалдаг.

Математикийн нэг салбар болох комбинаторик үүссэн нь мөрийтэй тоглоомын онолын тухай Б.Паскаль, П.Фермат нарын бүтээлүүдтэй холбоотой. Комбинаторын аргыг хөгжүүлэхэд асар их хувь нэмэр оруулсан Г.В. Лейбниц, Ж.Бернулли, Л.Эйлер нар.

Францын философич, зохиолч, математикч, физикч Блез Паскаль (1623-1662) математикийн гайхалтай чадвараа эрт харуулжээ. Паскалийн математикийн сонирхлын хүрээ маш олон янз байсан. Паскаль проекцийн геометрийн үндсэн теоремуудын нэгийг нотолсон (Паскалын теорем), нийлбэрийн машин (Паскалын нэмэх машин) зохион бүтээсэн, бином коэффициентийг (Паскалын гурвалжин) тооцоолох аргыг өгсөн, математик индукцийн аргыг анх удаа зөв тодорхойлж, хэрэгжүүлсэн хүн юм. нотлох үүднээс, мөн хязгааргүй жижиг анализыг хөгжүүлэхэд чухал алхам хийсэн чухал үүрэгмагадлалын онолын гарал үүсэл. Гидростатикт Паскаль үндсэн хуулиа (Паскалын хууль) бий болгосон. Паскалийн "Аймагт бичсэн захидал" нь Францын сонгодог зохиолын шилдэг бүтээл байв.

Готфрид Вильгельм Лейбниц (1646-1716) - Германы гүн ухаантан, математикч, физикч, зохион бүтээгч, хуульч, түүхч, хэл шинжлэгч. Математикийн хувьд тэрээр И.Ньютонтой хамт дифференциал ба интеграл тооцоог боловсруулсан. Тэрээр комбинаторикт чухал хувь нэмэр оруулсан. Ялангуяа түүний нэр нь тооны онолын асуудлуудтай холбоотой байдаг.

Готфрид Вильгельм Лейбниц нь тийм ч гайхалтай дүр төрхгүй байсан тул нэлээд энгийн хүн мэт сэтгэгдэл төрүүлжээ. Парист нэг өдөр тэрээр өөрийн таньдаг гүн ухаантны номыг худалдаж авна гэж найдаж номын дэлгүүрт оров. Нэгэн зочин энэ номын талаар асуухад номын худалдагч түүнийг толгойноосоо хөл хүртэл шалгаж үзээд: "Чамд яагаад хэрэгтэй байна вэ? Чи үнэхээр ийм ном унших чадвартай юу?" Эрдэмтэн хариулж амжаагүй байтал номын зохиогч өөрөө "Агуу Лейбницт мэндчилгээ дэвшүүлье!" Гэж дэлгүүрт оров. Энэ бол үнэхээр алдартай Лейбниц байсан бөгөөд ном нь эрдэмтдийн дунд маш их эрэлт хэрэгцээтэй байсан гэдгийг худалдагч ойлгохгүй байв.

Ирээдүйд дараахь чухал үүрэг гүйцэтгэнэ

Лемма.Элементүүдийн олонлогт, мөн элементүүдийн олонлогт оруулаарай. Дараа нь бүх ялгаатай хосуудын тоо тэнцүү байх болно.

Баталгаа.Үнэн хэрэгтээ, олонлогийн нэг элементээр бид ийм өөр хос, нийтдээ олон тооны элементүүдийг хийж чадна.

Байршил, сэлгэлт, хослолууд

Гурван элементийн багцтай болцгооё. Эдгээр хоёр элементийг бид ямар аргаар сонгож болох вэ?

Тодорхойлолт.Элемент тус бүрээр нь янз бүрийн элементүүдийн олонлогийн зохицуулалт гэдэг нь өгөгдсөн элементүүдээс бүрдсэн элементүүдээс бүрдэх ба элементүүдийн өөрөө эсвэл элементүүдийн дарааллаар ялгаатай хослолууд юм.

Элементүүдийн багцын бүх зохицуулалтын тоог элементээр (франц хэлний "зохицуулалт" гэсэн үгийн эхний үсгээс авсан) гэж тэмдэглэнэ.

Теорем.Элементийн багц элементийг элемент тус бүрээр нь байрлуулах тоо тэнцүү байна

Баталгаа.Бидэнд элементүүд байгаа гэж бодъё. Байршуулах боломжтой байг. Бид эдгээр байршлыг дарааллаар нь барих болно. Эхлээд эхний байршуулах элементийг тодорхойлъё. Өгөгдсөн элементүүдийн багцаас үүнийг янз бүрийн аргаар сонгож болно. Эхний элементийг сонгосны дараа хоёр дахь элементийг сонгох гэх мэт сонголтууд хэвээр байна. Ийм сонголт бүр нь шинэ байрлалыг өгдөг тул эдгээр бүх сонголтыг бие биетэйгээ чөлөөтэй хослуулж болно. Тиймээс бидэнд байна:

Жишээ.Таван өнгийн материал байвал туг өөр өөр өнгийн гурван хэвтээ зураасаар хэдэн янзаар бүтэх вэ?

Шийдэл.Шаардлагатай тооны гурван хамтлаг туг:

Тодорхойлолт.Элементүүдийн багцыг солих нь элементүүдийг тодорхой дарааллаар байрлуулах явдал юм.

Тиймээс гурван элементийн олонлогийн бүх өөр өөр сэлгэлтүүд байна

Элементүүдийн бүх сэлгэлтийн тоог тэмдэглэсэн (Францын "сэлгэн залгалт", "хөдөлгөөн" гэсэн үгийн эхний үсгээс). Тиймээс бүх өөр өөр орлуулалтын тоог томъёогоор тооцоолно

Жишээ.Шатрын тавцан дээр 8 дэгээг бие биенээ онохгүйгээр хэдэн янзаар байрлуулах вэ?

Даалгавар . Бүх захиалсан багцын тоог тодорхойл урт r, олонлогийн элементүүдээс бүрдэх боломжтой X (
), хэрэв элемент бүрийн сонголт
, бүх иж бүрдэлээс үйлдвэрлэгддэг X.

Захиалсан багц
нь декартын бүтээгдэхүүний элемент юм
, бүрдэнэ rижил үржүүлэгчид X. Бүтээгдэхүүний дүрмийн дагуу багцын элементийн тоо
тэнцүү байна
. Бид томъёог гаргаж авсан
.

Жишээ. Бүх арван оронтой тоог ашиглан дөрвөн оронтой хэдэн утасны дугаар хийж болох вэ?

Энд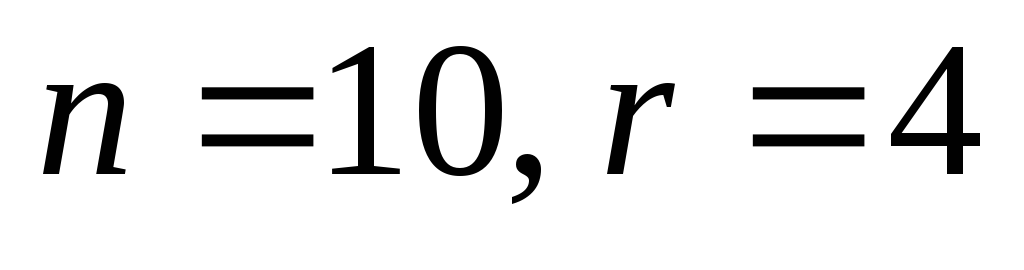
, тоо хэмжээ утасны дугааруудтэнцүү байна

2.1.5. Дахин давталтгүйгээр байршуулах

Даалгавар . Хичнээн багц захиалсан бэ
-аас бүрдэж болно nбагцын элементүүд X, хэрэв олонлогийн бүх элементүүд өөр бол?

Эхний элемент сонгож болно nарга замууд. Хэрэв эхний элемент аль хэдийн сонгогдсон бол хоёр дахь элемент та зөвхөн сонгох боломжтой
арга замууд, хэрэв аль хэдийн сонгосон бол
бүрэлдэхүүн
, дараа нь элемент сонгож болно
арга замууд (аль хэдийн сонгосон элементийг давтахыг зөвшөөрөхгүй). Бүтээгдэхүүний дүрмээр бид авдаг

Энэ томьёог тэмдэглэгээг ашиглан өөрөөр бичдэг
. Учир нь

.

Жишээ. Хэрэв 20 хүн оролцсон бол олимпиадын ялагчдын хэдэн өөр жагсаалт (эхний, хоёрдугаар, гуравдугаар байр) байж болох вэ? Хүн үү?

Энд
, шаардлагатай тоо байна

2.1.6. Дахин давтагдахгүйгээр солих

Давталтгүйгээр байршуулах онцгой тохиолдлыг авч үзье: хэрэв
, дараа нь багцын бүх элементүүд байршуулалтад оролцоно X, өөрөөр хэлбэл дээж нь ижил найрлагатай бөгөөд зөвхөн элементүүдийн дарааллаар бие биенээсээ ялгаатай. Ийм дээжийг нэрлэдэг орлуулалт . -аас солих тоо nэлементүүдийг төлөөлдөг :

Жишээ.Зургаан хүн цалингаа авахыг хүсвэл кассанд хэдэн янзаар жагсах вэ?

2.1.7. Дахин давтагдах өөрчлөлтүүд

Багцыг нь тавь Xорно кянз бүрийн элементүүд:
.Давталттай солих найрлага
Бид захиалсан уртын багцыг дуудах болно
, аль элемент уулздаг нэг удаа
. Ийм орлуулалтын тоог тэмдэглэв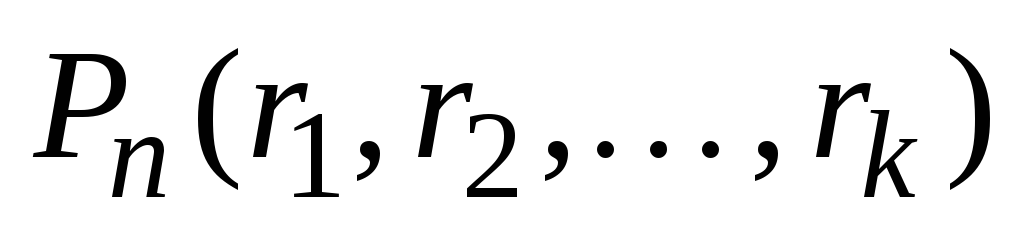
.

Жишээ. Захидлуудаас
найрлагыг давтах замаар орлуулалт бичье
. Түүний урт
, мөн захидал а 2 удаа ордог, б- 2 удаа, в- нэг удаа. Ийм солих нь жишээлбэл,
эсвэл
.

Давталттай сэлгэлтийн тооны томьёог гаргаж авцгаая. Оролцоонд орсон бүх ижил элементүүдийг өөр өөр индексээр дугаарлаж үзье, өөрөөр хэлбэл. дахин зохион байгуулахын оронд
бид авдаг
. Одоо сэлгэцийн бүх элементүүд өөр өөр байдаг бөгөөд ийм солих тоо нь тэнцүү байна
. Эхний элемент нь сонголтод тохиолддог нэг удаа. Эхний элементээс индексүүдийг хасъя (бидний жишээн дээр бид сэлгэлтийг авдаг
), харин өөр өөр сэлгэлтийн тоо багасах болно 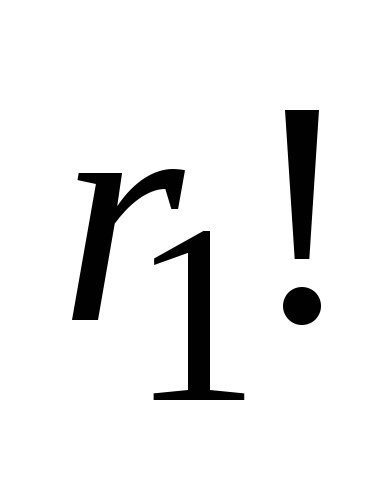удаа, учир нь Хэрэв бид ижил элементүүдийн дарааллыг өөрчлөх юм бол бидний дээж өөрчлөгдөхгүй. Хэрэв бид хоёр дахь элементээс индексүүдийг хасвал сэлгэцийн тоо багасах болно нэг удаа. Гэх мэт, тоо бүхий элемент хүртэл к– сэлгэлтийн тоо багасна нэг удаа. Бид томъёог авдаг

Жишээ. Та "дамжуулах" гэсэн үгийн үсгийг дахин цэгцлэхэд хэдэн өөр "үг" авах боломжтой вэ?

Энэ үгэнд "e" ба "a" үсэг хоёр удаа, үлдсэн хэсэг нь тус бүр нэг удаа гарч ирдэг. Бид найрлагыг давтах замаар дахин зохион байгуулах тухай ярьж байна
урт. Ийм солих тоо нь тэнцүү байна

2.1.8. Хослолууд

Даалгавар . Хэдэн өөр багц rэлементүүдийг агуулсан багцаас бүрдэж болно nэлементүүд?

Бид эхлээд захиалсан багцуудыг зохиох болно rтус бүр дэх элементүүд. Ийм багцын тоо (эдгээр нь nэлементүүд r) тэнцүү байна
. Одоо бид элементүүдийг бичсэн дараалал нь бидэнд хамаагүй гэдгийг анхаарч үздэг. Үүний зэрэгцээ, -аас өөр өөр байршил, зөвхөн элементүүдийн дарааллаар ялгаатай, бид нэг хослолыг авдаг. Жишээлбэл, хоёр өөр байршил
Тэгээд
хоёр элемент нь нэг хослолд тохирч байна
. Тиймээс хослолуудын тоо В 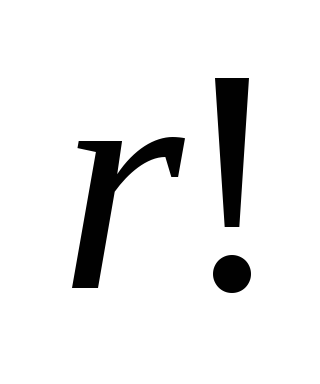нэг удаа бага тообайршуулалт :

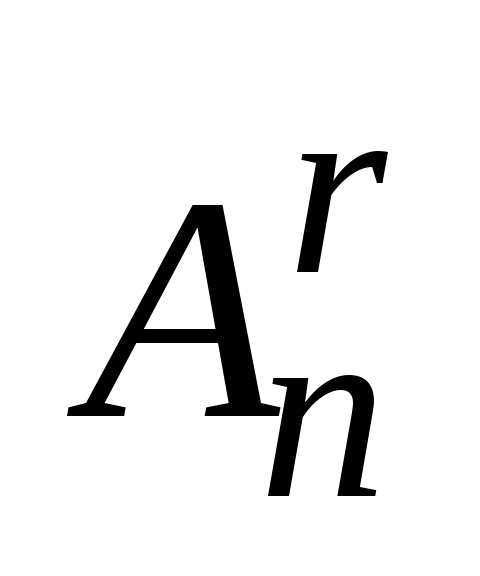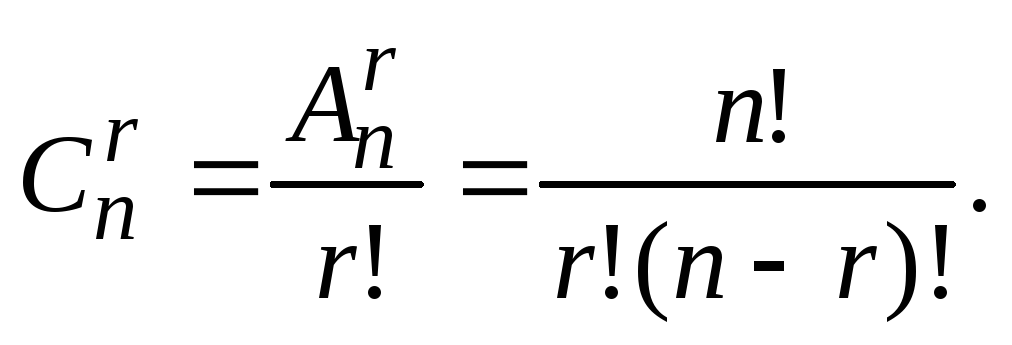
Жишээ. Найман арчигчаас гурвыг нь сонгох хэд хэдэн арга байдаг

Комбинаторик - өгөгдсөн объектуудаас тодорхой нөхцлийн дагуу хэдэн өөр хослол хийж болох тухай асуултуудыг судалдаг математикийн салбар.

Комбинаторик нь 16-р зуунд үүссэн. Эхний комбинатын асуудал нь мөрийтэй тоглоомтой холбоотой байв. Өнөөдөр тээврийн асуудлыг шийдвэрлэх, үйлдвэрлэлийн төлөвлөгөө гаргах, бүтээгдэхүүн борлуулахад комбинатын аргыг ашигладаг. Комбинаторик ба асуудлуудын хоорондын холбоо тогтоогдсон шугаман програмчлал, статистик. Комбинаторикийг шифр бичих, тайлах, мэдээллийн онолын бусад асуудлыг шийдвэрлэхэд ашигладаг.

Комбинаторын аргууд нь цэвэр математикийн асуудалд чухал үүрэг гүйцэтгэдэг - бүлгүүдийн онол ба тэдгээрийн төлөөлөл, геометрийн үндсийг судлах, ассоциатив бус алгебрууд гэх мэт.

Комбинаторын бодлогын жишээ. Хэдэн ширхэг гурван оронтой тооТа 0, 2, 4, 6, 8 тоонуудыг тус бүрийг нэгээс илүүгүй ашиглаж болох уу?

Iарга зам. Ийм бүх тоог бичихийг хичээцгээе. Эхний байр нь 0-ээс бусад тоо байж болно. Жишээ нь: 2. Хоёрдугаар байр нь 0, 4, 6, 8-ын аль ч тоо байж болно. Энэ нь 0 байг. Дараа нь гурав дахь тоо нь 4, 6, 8-ын аль нь ч байж болно. Бид гурван тоо авдаг

0-ийн оронд 4-ийг хоёрдугаарт тавьж, гурав дахь тоог 0, 6, 8 гэж бичиж болно.

Үүнтэй адилаар бид эхний ээлжинд 2 дугаартай гурван оронтой тооны дахин хоёр гурвалсан тоог авна.

Бичсэн 12-ыг эс тооцвол эхний ээлжинд 2-той гурван оронтой тоо бол нөхцөлийг хангасан тоо байхгүй.

Хэрэв бид эхний ээлжинд 4-ийн тоог бичиж, 0, 2, 6, 8 тоонуудаас үлдсэнийг нь сонговол 12 тоо гарч ирнэ.

Эхний ээлжинд 6, эхний ээлжинд 8 дугаартай ижил тооны гурван оронтой тоог хийж болно. Тиймээс шаардлагатай хэмжээ нь:

Эдгээр тоонууд нь:

204, 206, 208, 240, 246, 248, 260, 264, 268, 280, 284, 286;

402, 406, 408, 420, 426, 428, 460, 462, 468, 480, 482, 486;

602, 604, 608, 620, 624, 628, 640, 642, 648, 680, 682, 684;

802, 804, 806, 820, 824, 826, 840, 842, 846, 860, 862, 864.

Хариулт: 48. ◄

Өмнөх асуудлыг шийдвэрлэхийн тулд бидний хэрэглэж байсан үндэслэлийн аргыг нэрлэдэг боломжит хувилбаруудыг хайж олох .

Нэмэх, үржүүлэх дүрэм

Комбинаторын нэмэх дүрэм("эсвэл" дүрэм - комбинаторикийн үндсэн дүрмүүдийн нэг бөгөөд хэрэв байгаа бол гэж заасан байдаг n элементүүд ба элемент А 1сонгож болно м 1 арга зам, элемент А 2сонгож болно м 2 А n сонгож болно м n арга, дараа нь сонгох эсвэл А 1, эсвэл А 2, эсвэл, гэх мэт А n Чадах

м 1 + м 2 + ... + м n

арга замууд.

Жишээлбэл, 9 машин, 7 бамбарууш, 3-аас хүүхдэд зориулсан бэлгийг сонго төмөр замуудЧадах

арга замууд.

Хариулт: 19. ◄

Үржүүлэх дүрэм ("ба" дүрэм) - өөр нэг чухал дүрэмкомбинаторик. Түүний хэлснээр хэрэв элемент А 1сонгож болно м 1 арга зам, элемент А 2сонгож болно м 2 арга зам гэх мэт, элемент А n сонгож болно м n арга, дараа нь элементүүдийн багц ( А 1, А 2, ... , А n ) сонгож болно

м 1 · м 2 · ... · м n

арга замууд.

Жишээлбэл.

1) Та 9 машин, 7 бамбарууш, 3 төмөр замаас сонголтоо хийж хүүхэддээ автомашин, бамбарууш, төмөр зам бэлэглэх боломжтой.

9 7 3 = 189

арга замууд.

Хариулт: 189.

2) Дээр дурдсан асуудлыг шийдэхийн тулд үржүүлэх дүрмийг ашиглая: 0, 2, 4, 6, 8-ын цифрүүдээс хэдэн гурван оронтой тоо гаргаж, тоог бичихдээ тус бүрийг нэгээс илүүгүй удаа ашиглаж болох вэ?

IIарга зам.

0 нь эхлээд орж болохгүй, энэ нь эхний цифрийг 2, 4, 6, 8 - 4 аргаас сонгох ёстой гэсэн үг;

хоёр дахь цифр нь үлдсэн дөрвөн аргын аль нэг нь байж болно - 4 аргын;

Гурав дахь цифрийг үлдсэн 3-3 аргын дундаас сонгож болно.

Тиймээс, шаардлагатай гурван оронтой тооны тоо:

4 4 3 = 48.

Хариулт: 48. ◄

Дахин зохион байгуулалт

Маш их n элементүүд гэж нэрлэдэг захиалсан , хэрэв түүний элемент тус бүрд 1-ээс натурал тоо өгөгдсөн бол n .

Дахин зохион байгуулалт -аас n элементүүд нь ямар ч дараалсан багц юм n элементүүд.

Жишээлбэл, 4 элементээс ♦ ♣ ♠ Дараах 24 өөрчлөлтийг хийж болно:

♦ ♣ ♠	♦ ♣ ♠	♣ ♦ ♠	♠ ♦ ♣
♦ ♠ ♣	♦ ♠ ♣	♣ ♦ ♠	♠ ♦ ♣
♦ ♣ ♠	♣ ♦ ♠	♣ ♦ ♠	♠ ♦ ♣
♦ ♣ ♠	♣ ♠ ♦	♣ ♠ ♦	♠ ♣ ♦
♦ ♠ ♣	♠ ♦ ♣	♣ ♠ ♦	♠ ♣ ♦
♦ ♠ ♣	♠ ♣ ♦	♣ ♠ ♦	♠ ♣ ♦

◄

-аас солих тоо n элементүүдийг ихэвчлэн тодорхойлсон байдаг П n . Боломжит хувилбаруудыг хайж олох замаар үүнийг шалгахад хялбар байдаг

P 1 = 1; P2 = 2; P 3 = 6; P 4 = 24.

Ерөнхийдөө, боломжит сэлгэлтийн тоо -аас n элементүүд нь бүгдийн бүтээгдэхүүнтэй тэнцүү байна натурал тоонууд 1-ээс n , тэр бол n! ("en factorial"-ыг уншина уу):

П n= 1 · 2 · 3 · ... · ( n- 1 ) · n = n!.

П.-ийн хувьд nдавтагдах томъёо хүчинтэй байна:

П n = nП n- 1 .

Факториалын утгыг зөвхөн натурал тоонд төдийгүй 0-д тодорхойлно.

0! = 1 .

Бүхэл тоонуудын факториалуудын хүснэгт 0 өмнө 10
n		1	2	3	4	5	6	7	8	9	10
n!	1	1	2	6	24	120	720	5 040	40 320	362 880	3 628 800

Жишээлбэл, хоёр хүү, хоёр охин зэрэгцэн суухгүй бол театрт 1-ээс 10-р байр хүртэл 5 хүү, 5 охин нэг эгнээнд хэдэн янзаар суух вэ?

Ижил тооны аргатай хоёр тохиолдол байдаг: 1) хөвгүүд - сондгой газар, охид тэгш газар, 2) эсрэгээр.

Эхний тохиолдлыг авч үзье. Хөвгүүд сондгой суудалд сууж болно

P5 = 120

арга замууд. Тэгш тоотой газруудад охидод зориулсан маш олон арга бий. Үржүүлэх дүрмийн дагуу хөвгүүд сондгой газар, охид тэгш газар байрлаж болно

120 · 120 = 14,400

арга замууд. Тэгэхээр, нийтээрээ

14 400 + 14 400 = 28 800.

Хариулт: 28,800. ◄

Дахин давтагдах өөрчлөлтүүд

Давталттай солих -аас n элементүүд, түүний дотор к өөр, байсаар байхад n 1 эхний төрлийн үл ялгагдах элементүүд, n 2 хоёр дахь төрлийн үл ялгагдах элементүүд гэх мэт, n к үл ялгагдах элементүүд к -р төрөл (хаана n 1 + n 2 + … + н к = n ), эдгээр элементүүдийн аливаа зохицуулалт n янз бүрийн газар.

Урт давтагдах сэлгэлтийн тоо n -аас к өөр өөр элементүүд, дагуу авсан n 1 , n 2 , …, н к удаа бүрийг дараах байдлаар тэмдэглэж, тооцоолно:$$P_(n_1,n_2, ... , n_k)=\frac(n){n_1!n_2! ... n_k!}~.$$!}

Жишээлбэл, 1, 2, 2, 3, 3, 3, 4, 4, 4, 4 гэсэн цифрүүдээс хэдэн өөр арван оронтой тоо гаргаж болох вэ?

IN энэ тохиолдолд: n = 10, n 1 = 1, n 2 = 2, n 3 = 3, n 4 = 4,$$P_(1, 2, 3, 4)=\frac(10{1!2! 3! 4!}=\frac{10!}{1!2! 3! 4!}=12~600.$$!}

Хариулт: 12,600. ◄

Байршлуулалт

n элементийг m дарааллаар байрлуулснаар(m ≤ n) м өгөгдлөөс тодорхой дарааллаар авсан элементүүд n элементүүд.

-аас хоёр байр nэлементүүд мтэдгээр нь элементүүдийн хувьд эсвэл тэдгээрийн зохион байгуулалтын дарааллаар ялгаатай бол өөр гэж үзнэ.

Жишээлбэл, бүх байршлыг эмхэтгэе дөрвөн элемент A B C Dтус бүр хоёр элемент:

A B; A C;A D;

B A; B C; B D;

C A; C B; C D;

D A; D B; D C.

◄

Бүх байршлын тоо nэлементүүд м\(A_n^m\) (унших: " А-аас n By м") бөгөөд дараах томъёог ашиглан тооцоолно:$$A_n^m=n\cdot (n-1)\cdot (n-2)\cdot ...\cdot (n-m+1)\\A_n^ m= \фрак(n{(n-m)!}$$!}

Даалгаврын жишээ.

1) -аас байршуулах ойлголтыг ашиглацгаая n элементүүд м Өмнө нь хоёр удаа ярилцаж байсан асуудлыг шийдэхийн тулд: 0, 2, 4, 6, 8-ын цифрүүдээс хэдэн гурван оронтой тоо гаргаж, тоог бичихдээ тус бүрийг нэгээс илүүгүй удаа ашиглаж болох вэ?

I IIарга зам.

Эхний цифрийг 2, 4, 6, 8 олонлогоос дөрвөн аргаар сонгож болно. Эдгээр тохиолдол бүрт хоёр, гурав дахь цифрүүдийн хосуудын тоо нь үлдсэн 4 цифрийн байршлын тоотой 2-оор тэнцүү байна. Энэ нь шаардлагатай гурван оронтой тоо нь: $$4\cdot A_4^ 2=4\cdot\frac(4) гэсэн үг.{(4-2)!}=4\cdot \frac{4!}{2!}=4\cdot (3\cdot 4)=48.$$Ответ: 48.!}

2) Сансарт нисэхийн тулд зургаан хүний ​​бүрэлдэхүүнтэй баг байх шаардлагатай. Үүнд: хөлөг онгоцны командлагч, түүний нэг ба хоёрдугаар офицер, хоёр нисэх инженер, нэг нь ахлах, нэг эмч байх ёстой. Команд штабыг 20 нисгэгч, нисэх инженерийг 15 мэргэжилтнээс, эмчийг 5 эмчээс сонгож байна. Багийг хэдэн аргаар ажиллуулж болох вэ?

Командлах боловсон хүчнийг сонгоход тушаал чухал байдаг тул командлагч болон түүний хоёр туслахыг \(A_(20)^3\) аргаар сонгож болно. Нислэгийн инженерүүдийн дараалал бас чухал бөгөөд энэ нь тэднийг сонгох \(A_(15)^2\) арга байдаг гэсэн үг. Ганцхан эмч байна, түүнд сонголт бий 5 арга замууд. Комбинаторын үржүүлгийн дүрмийг ашиглан хөлөг онгоцны боломжит багийн тоог олцгооё:$$A_(20)^3\cdot A_(15)^2\cdot 5=\frac(20){17!}\cdot \frac{15!}{13!}\cdot 5=(18\cdot 19\cdot 20)\cdot (14\cdot 15)\cdot 5=7~182~000.$$Ответ: 7 182 000. !} ◄

Хэрэв энэ нь тодорхой байна m = n , дараа нь$$A_n^m=A_n^n=P_n=n!.$$

Энэ нь бас үнэн юм бол m = n - 1 , дараа нь$$A_n^(n-1)=A_n^n=P_n=n!.$$

Давталт бүхий байрлалууд

Ердийн байршуулалтаас гадна бас байдаг давталт бүхий байршуулалт эсвэл буцаан олголттой дээж .

Байг n янз бүрийн объектууд. Тэднээс сонголт хийцгээе м хэсэг, дээр ажиллаж байна дараах зарчмаар. Аль нэгийг нь авъя, гэхдээ бид үүнийг ямар ч эгнээнд байрлуулахгүй, зүгээр л 1-р дугаарын доор нэрийг нь бичээд дараа нь объектыг бусад хэсэгт буцааж өгнө. Дараа нь дахин n Нэг объектыг (магадгүй саяхан авсан объектыг оруулаад) сонгоод, нэрийг нь 2-оор тэмдэглээд, объектыг буцааж өгье. Биднийг авах хүртэл гэх мэт м гарчиг.

Дахин давтагдах байршлыг \(\overline(A)_n^m\) гэж тэмдэглэсэн бөгөөд үржүүлэх дүрмийн дагуу $$\overline(A)_n^m=n^m.$$Томьёог ашиглан тооцоолно. энд бид хэзээ тохиолдлыг зөвшөөрдөг m > n , өөрөөр хэлбэл нийт сонгогдсон объектуудаас олон байна. Энэ нь гайхах зүйл биш юм: объект бүрийг "ашигласан" дараа буцааж буцааж, дахин ашиглах боломжтой.

Жишээлбэл, тэмдэгт бүр нь 0-ээс 9 хүртэлх тоо эсвэл латин цагаан толгойн үсэг (ижил жижиг, том үсэг - нэг тэмдэгт) бөгөөд давтаж болох зургаан тэмдэгтээс бүрдэх нууц үгийн сонголтуудын тоо тэнцүү байна. руу: $$\overline(A)_(10 +26)^6=\overline(A)_(36)^6=36^6=2~176~782~336.$$Хэрэв жижиг үсэг болон том үсэгнүүдөөр өөр тэмдэгтүүд гэж тооцогддог (ихэвчлэн тохиолддог), дараа нь боломжит нууц үгийн тоо улам их болно: $$\overline(A)_(10+26+26)^6=\overline(A)_(62) ^6= 62^6=56~800~235~584.$$

◄

Хослолууд

n элементийн хослол, тус бүр нь m(m ≤ n) -аас бүрдсэн аливаа багц юм м өгөгдлөөс сонгосон элементүүд n элементүүд.

Хослолын байршлаас ялгаатай нь элементүүдийг ямар дарааллаар жагсаах нь хамаагүй. Хоёр хослол nэлементүүд мнаад зах нь нэг элементээр ялгаатай байвал өөр гэж үзнэ.

Жишээлбэл, дөрвөн элементийн бүх хослолыг хийцгээе A B C Dтус бүр хоёр элемент:

A B; A C;A D;

B C; B D;

C D.

◄

Бүх хослолын тоо nэлементүүд м\(C_n^m\) тэмдэглэнэ (унших: " C-аас n By м") бөгөөд дараах томъёог ашиглан тооцоолно:$$C_n^m=\frac(A_n^m)(P_m)$$$$C_n^m=\frac(n\cdot (n-1)\cdot (n) -2 )~\cdot~ ...~\cdot~ (n-m+1))(1\cdot2\cdot3~\cdot~...~\cdot ~m)$$$$C_n^m=\ frac( n{m!\cdot (n-m)!}.$$!}

Даалгаврын жишээ.

1) Сургуулийн засварын баг нь 12 будагч, 5 мужаанаас бүрддэг. Үүнээс биеийн тамирын заалны засварын ажилд 4 будагчин, 2 мужаан ажиллах ёстой. Үүнийг хэдэн аргаар хийж болох вэ?

Сонгосон дөрвийн зураачдын дараалал, сонгосон хос тус бүрийн мужаануудын дараалал хамаагүй тул комбинатор үржүүлэх дүрмийн дагуу шаардлагатай тооны арга нь:$$C_(12)^4-тэй тэнцүү байна. \cdot C_5^2 =\frac(12{4!\cdot 8!}\cdot \frac{5!}{2!\cdot 3!}=\frac{9\cdot10\cdot11\cdot12}{1\cdot2\cdot3\cdot4}\cdot \frac{4\cdot5}{1\cdot 2}=4~950.$$Ответ: 4 950. !} ◄

2) Ангид 30 сурагч, 13 хүү, 17 охин. Энэ ангийн 7 сурагчтай багийг ядаж нэг охинтой байх ёстой бол хэдэн аргаар бүрдүүлэх вэ?

Нэг ангиас 7 хүнтэй байж болох бүх багийн тоо нь \(C_(30)^7\). Зөвхөн хөвгүүдтэй багуудын тоо нь \(C_(13)^7\). Энэ нь дор хаяж нэг охинтой багуудын тоо:$$C_(30)^7 - C_(13)^7 =\frac(30) гэсэн үг.{7!\cdot 23!} - \frac{13!}{7!\cdot 6!}=2~035~800-1~716=2~034~084.$$Ответ: 2 034 084. !} ◄

Давталттай хослолууд

Түүнээс гадна ердийн хослолуудавч үзэж байна давталттай хослолууд .

Багцанд байгаарай n объектууд. Тэднээс сонголт хийцгээе м хэсэг, дараах зарчмаар ажилладаг. Аль нэгийг нь авъя, гэхдээ бид үүнийг ямар ч эгнээнд оруулахгүй, зүгээр л бичээд дараа нь объектыг бусад хэсэгт буцааж өгнө. Дараа нь дахин n Нэг объектыг сонгоод (магадгүй өмнө нь авч, бичсэнийг оруулаад), нэрийг нь бичээд объектыг буцааж буцааж өгье. Биднийг авах хүртэл гэх мэт м гарчиг.

Давталттай байршуулалтаас үндсэн ялгаа нь энэ тохиолдолд жагсаалтын элементүүдийг дугаарлахгүй байх явдал юм. Жишээлбэл, жагсаалт "А, В, А, Б"болон жагсаалт "A, A, B, C"адилхан гэж үздэг.

Давталттай хослолуудыг \(\overline(C)_n^m\) гэж тэмдэглэсэн бөгөөд $$\overline(C)_n^m=P_(m,~n-1)=\frac((m+) томъёог ашиглан тооцоолно. n-1){m!\cdot (n-1)!}.$$И ещё один способ записи той же формулы:$$\overline{C}_n^m=C_{m+n-1}^m=\frac{(m+n-1)!}{m!\cdot (n-1)!}.$$Заметим, что подобно размещениям с повторениями, допустим случай, когда !} m > n , өөрөөр хэлбэл нийт сонгогдсон объектуудаас олон байна. Үнэн хэрэгтээ объект бүрийг "ашигласан" дараа буцааж өгдөг бөгөөд дахин дахин ашиглах боломжтой.

Жишээлбэл, 4 төрлийн бялуу худалдаалагдаж байгаа бол 7 бялууг чихрийн цехээс хэдэн аргаар худалдаж авч болохыг олж мэдье?

Төрөл бүрийн бялууны тоог 7-оос доошгүй гэж үзэх нь зүйн хэрэг бөгөөд хэрэв хүсвэл зөвхөн нэгээс нь бялуу авч болно. Худалдан авсан бялууг хайрцагт байрлуулах дараалал нь чухал биш тул бид давталттай хослолуудтай харьцаж байна. Та 4 төрлөөс 7 бялуу сонгох шаардлагатай тул шаардлагатай тооны арга нь:$$\overline(C)_4^7=\frac((7+4-1){7!\cdot (4-1)!}=\frac{10!}{7!\cdot 3!}=\frac{8\cdot 9\cdot 10}{1\cdot 2\cdot 3}=120.$$!}

Хариулт: 120. ◄

Ньютоны бином ба бином коэффициентүүд

Тэгш байдал$$(x+a)^n=C_n^0x^na^0+C_n^1x^(n-1)a^1+...+C_n^mx^(n-m)a^m+...+ C_n^nx^0a^n$$ дуудагдсан Ньютоны бином эсвэл Ньютоны томъёо . Баруун хэсэгтэгш байдал гэж нэрлэдэг нийлбэр болгон хоёр талын тэлэлт , ба коэффициентүүд \(C_n^0,~C_n^1,~...~,~C_n^n\) - бином коэффициент .

Бином коэффициентийн шинж чанарууд:

\(~~~~~~~~1.~~C_n^0=C_n^n=1\\ ~~~~~~~~2.~~C_n^m=C_n^(n-m)\\ ~~ ~~~~~~3.~~C_n^m=C_(n-1)^(m-1)+C_(n-1)^(m)\\ ~~~~~~~~4.~ ~C_n^0+C_n^1+C_n^2+~...~+C_n^n=2^n\\ ~~~~~~~~5.~~C_n^0+C_n^2+C_n^ 4+~... =C_n^1+C_n^3+C_n^5+~...=2^(n-1)\\ ~~~~~~~~6.~~C_n^n+C_ (n+1)^n+C_(n+2)^n+~...~+C_(n+m-1)^n=C_(n+m)^(n+1)\\ \)

Бином тэлэлтийн шинж чанарууд:

1. Өргөтгөх бүх гишүүний тоо нь хоёр гишүүний илтгэгчээс нэг их,

Энэ нь тэнцүү юм n+ 1 .

2. Үзүүрийн нийлбэр x Тэгээд а тэлэлтийн гишүүн бүр нь биномын экспоненттай тэнцүү,

тэр бол (n - m) + m = n .

3. Өргөтгөх ерөнхий нэр томъёо (тэмдэглэсэн Т n+1 ) $$T_(n+1)=C_n^m x^(n-m)a^m,~~~~m=0,~1,~2,~...~,~n.$$ хэлбэртэй байна.

Паскалийн гурвалжин

Бином илтгэгч тус бүрийн хувьд бином коэффициентийн бүх боломжит утгууд (хослолын тоо). n хязгааргүй гурвалжин хүснэгт хэлбэрээр бичиж болно. Энэ хүснэгтийг нэрлэдэг Паскалийн гурвалжин:

					\(C_0^0\)
				\(C_1^0\)		\(C_1^1\)
			\(C_2^0\)		\(C_2^1\)		\(C_2^2\)
		\(C_3^0\)		\(C_3^1\)		\(C_3^2\)		\(C_3^3\)
	\(C_4^0\)		\(C_4^1\)		\(C_4^2\)		\(C_4^3\)		\(C_4^4\)
\(C_5^0\)		\(C_5^1\)		\(C_5^2\)		\(C_5^3\)		\(C_5^4\)		\(C_5^5\)
	. . .				. . .				. . .

Энэ гурвалжинд эгнээ тус бүрийн туйлын тоо 1-тэй тэнцүү байна. Үнэхээр \(C_n^0=C_n^n=1\). Мөн туйлын бус тоо бүр нь өмнөх мөрийн дээрх хоёр тооны нийлбэртэй тэнцүү байна: \(C_n^m=C_(n-1)^(m-1)+C_(n-1)^(m) )\).

Тиймээс энэ гурвалжин нь \(C_n^m\) тоог тооцоолох өөр (давтагдах) аргыг санал болгож байна:

n = 0									1
n = 1								1		1
n = 2							1		2		1
n = 3						1		3		3		1
n = 4					1		4		6		4		1
n = 5				1		5		10		10		5		1
n = 6			1		6		15		20		15		6		1
n = 7		1		7		21		35		35		21		7		1
n = 8	1		8		28		56		70		56		28		8		1
...				...				...		...				...

MS EXCEL-д n элементийн сэлгэлтийн тоог тоолъё. Томьёог ашиглан бид бүх солих сонголтыг хуудсан дээр харуулна ( Англи хэлний орчуулганэр томъёо: орлуулах).

n элементийн багцыг солих нь элементүүдийг тодорхой дарааллаар байрлуулах явдал юм.

Олонлогийн элементүүд нь тоо, үсэг, ерөнхийдөө ямар ч объект байж болно. Хамгийн гол нь эдгээр элементүүд өөр өөр байдаг. Учир нь Аливаа объектыг тоотой холбож болно, дараа нь Сэлгээний хувьд тэд ихэвчлэн бүхэл тоонуудын төгсгөлтэй багцыг ашигладаг, жишээлбэл, (1; 2; 3; 4; 5). Хэдийгээр захидлын багцыг уран зохиолоос ихэвчлэн олж болно. Жишээлбэл, гурван элементийн олонлогийн (a, b, c) бүх өөр өөр сэлгэлтүүд байна abc, acb, бак, МЭӨ, такси, cba.

n элементийн сэлгэцийн тоо n байна! (фактор).

MS EXCEL-д факториалыг тооцоолохын тулд =FACT() функц байдаг. Англи хувилбар FACT(). Сэлгээний тоо n-тэй хамт маш хурдан өсөх нь тодорхой байна: n=7-ийн хувьд сэлгэлтийн тоо 5040 байна. Шударга ёсны үүднээс хэлэхэд ихэнхдээ солих сонголтуудыг өөрөө олох шаардлагагүй гэдгийг тэмдэглэх нь зүйтэй бөгөөд гол зүйл нь тэдний тоог ол.

Жич:Сэлгэцийг n=k-ийн байршлын онцгой тохиолдол гэж үзэж болно (нийтлэлийг үзнэ үү). Тиймээс та REST() функцийг ашиглан сэлгэцийн тоог тооцоолж болно. n=7-ийн хувьд Сэлгээний тоог = PERMANENT(7,7) томъёогоор тооцоолно.

Анхаарна уу: Та давталттай сэлгэлтийн талаар уншиж болно (элемент бүрийг сонгосны дараа элементүүдийг авсан олонлог руу буцаах).

Жишээ файлд өгөгдсөн n-ийн бүх Сэлгээг харуулах бүх нийтийн томьёог үүсгэсэн. Жишээлбэл, n=3-ийн хувьд.

Даалгавар

6 машин өөрбрэндүүд амьд үлдэх уралдаанд оролцдог: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Лада Калина, Volkswagen Polo. Бүх оролцогчдын дунд суудал хуваарилах боломжит хувилбаруудын тоог тодорхойл.

Бид 6 газар 6 машины сэлгэцийн тоог тодорхойлох хэрэгтэй. Тэдгээр. n=6. Ийм 720 солих байдаг нь харагдаж байна: =PREST(6,6) эсвэл 6! =БОДИТ(6)

Бүх сэлгэлтүүдийг олохын тулд жишээ файлыг ашиглацгаая.

Автомашины брэндүүдтэй тоон утгыг санамсаргүй байдлаар харьцуулж, брэндийн нэрсийн товчлолыг хийцгээе: LADA Granta (LG = 1), Hyundai Solaris (HS = 2), ...

Нүдэнд бичих замаар AT 5 6-р утгыг бид уралдаанд оролцож байсан газарт нь машин байрлуулах бүх сонголтыг тодорхойлно.

Анхаарна уу: Та нийтлэл дэх Байршлын тухай, мөн нийтлэлээс хослолын талаар уншиж болно.

Төрөл бүрийн асуудлыг шийдвэрлэхийн тулд бүх боломжит сэлгэлтийг тоолох шаардлагатай байж болно (нийтлэлийг үзнэ үү).

Сэлгээний урвуу

Сэлгээ бүрийн хувьд а 1, а 2, а 3,..., а n -ийн nбүхэл тоо 1, 2, 3, ..., n, урвуу нь хос ( аби, аи) хэрэв би< j выполняется а i> а j. Сэлгээний урвуу тоо нь сэлгэлт хэрхэн өсөх дарааллаар "эрэмбэлэгдээгүй" байгааг харуулдаг.

Жишээлбэл, 1, 2, 3, 4-ийн орлуулалт дахь урвуу өөрчлөлтийн тоо 0 (4 бүхэл тоонуудын сэлгэлтийг 1-ээс 4 хүртэл өсөх дарааллаар эрэмбэлсэн), 4, 3, 1, 2 нь 5, учир нь.:

• эхний элемент (i=1) нь 4 ба түүнээс их байна 3тоонууд (j=2, 3, 4-тэй), баруун талд байрладаг (4>3, 4>1, 4>2), i.e. бидэнд 3 урвуу байна;
• хоёр дахь элемент (i=2) нь 3 ба түүнээс их байна 2баруун талд байрлах тоонууд (j=3, 4-тэй) (3>1, 3>2), i.e. бидэнд өөр 2 урвуу байна;
• Гурав дахь элемент (i=3) нь 1-тэй тэнцүү бөгөөд баруун талд байрлах j=4-тэй тооноос бага (1)<2), то эта пара не является инверсией. Т.е. у перестановки 4, 3, 1, 2 число инверсий равно 3+2+0=5.

Жишээ файлд сэлгэлт бүрийн хувьд тоог урвуу байдлаар тооцдог.