Лопитал дүрмийн нарийвчилсан шийдэл бүхий онлайн хязгаарлалт. L'Hopital-ийн дүрэм: онол ба шийдлийн жишээ

Л'Хопиталын теорем(мөн Бернулли-Л'Хопитал дүрэм) - функцын хязгаарыг олох, хэлбэрийн тодорхойгүй байдлыг илрүүлэх арга ба . Энэ аргыг зөвтгөх теорем нь тодорхой нөхцөлд функцүүдийн харьцааны хязгаар нь тэдгээрийн деривативуудын харьцааны хязгаартай тэнцүү байна гэж заасан байдаг.

Яг нарийн үг хэллэг.

Дүрэм гэж хэлсэн бол функцууд е(x) ба g(x) дараах нөхцлүүдтэй байна:

тэгээд байна . Түүгээр ч барахгүй теорем нь бусад суурийн хувьд ч үнэн (заасан үндэслэлд нотолгоог өгөх болно).

Өгүүллэг.

Энэ төрлийн тодорхойгүй байдлыг илчлэх аргыг нийтэлсэн Лопиталонд хэвлэгдсэн "Хязгааргүй жижиг тоонуудын шинжилгээ" хэмээх бүтээлдээ 1696 жил. Энэхүү бүтээлийнхээ оршилд Лопитал нээлтүүдийг ямар ч эргэлзээгүйгээр ашигласан гэж тэмдэглэжээ Лейбницмөн Бернулли ах нар болон "Тэд хүссэн зүйлдээ зохиогчийн эрхээ нэхэмжилж байвал дургүйцэхгүй." Иоганн Бернулли L'Hopital-ийн бүх бүтээлийг нэхэмжилж, ялангуяа L'Hopital-ыг нас барсны дараа тэрээр "Тоологч нь бутархайн утгыг тодорхойлох Infinitesimal Analysis" сэтгүүлд хэвлэгдсэн миний аргын сайжруулалт гэсэн гайхалтай гарчигтай бүтээлээ хэвлүүлсэн. мөн хуваагч заримдаа алга болдог", 1704 .

Баталгаа.

Хандлага эцэс төгсгөлгүй жижиг

Функцуудын хязгаар тэгтэй тэнцүү байх (хэлбэрийн тодорхойгүй байдал гэж нэрлэгддэг) тохиолдолд теоремыг баталъя.

Учир нь бид функцуудыг харж байна еболон gзөвхөн цэгийн баруун цоорсон хагас хороололд а, Бид чадна Үргэлжилсэн арга замЭнэ үед тэдгээрийг дахин тодорхойлох: let е(а) = g(а) = 0. Заримыг нь аваарай xхэлэлцэж буй хагас хөршийн бөгөөд сегментэд хамаарах боломжтой теорем Коши. Энэ теоремоор бид дараахь зүйлийг олж авна.

,

гэхдээ е(а) = g(а) = 0, тиймээс .

Эцсийн хязгаарын хувьд болон

Хязгааргүйн төлөө

Энэ нь функцүүдийн харьцааны хязгаарын тодорхойлолт юм.

Хязгааргүй том харьцаа

Хэлбэрийн тодорхойгүй байдлын теоремыг баталъя.

Эхлэхийн тулд деривативын харьцааны хязгаарыг төгсгөлтэй ба тэнцүү гэж үзье А. Тэгээд хичээж байхдаа xруу абаруун талд энэ хамаарлыг дараах байдлаар бичиж болно А+ α, энд α - О(нэг). Энэ нөхцлийг бичье:

Засацгаая тсегментээс болон холбогдох теорем Кошибүгдэд нь xсегментээс:

Юунд хүргэж болох вэ дараагийн төрөл:

.

Учир нь x, хангалттай ойрхон байна а, илэрхийлэл нь утга учиртай; баруун талын эхний хүчин зүйлийн хязгаар нь нэгтэй тэнцүү байна (үүнээс хойш е(т) ба g(т) - тогтмолууд, a е(x) ба g(x) хязгааргүй байх хандлагатай байдаг). Иймээс энэ үржүүлэгч нь 1 + β-тэй тэнцүү байх ба энд β нь хязгааргүй жижиг функц юм. xруу абаруун талд. Бид энэ баримтын тодорхойлолтыг α-ийн тодорхойлолттой ижил утгыг ашиглан бичнэ.

Функцуудын харьцааг (1 + β) хэлбэрээр илэрхийлж болохыг бид олж мэдсэн. А+ α), ба .Аливаа өгөгдлийн хувьд функцуудын харьцаа хоорондын зөрүүний модуль ба Абага байсан нь функцүүдийн харьцааны хязгаар нь үнэхээр тэнцүү байна гэсэн үг юм А.

Бөмбөлөг нүдтэй бор шувууны сүргийг төсөөлөөд үз дээ. Үгүй ээ, энэ бол аянга биш, хар салхи биш, бүр гартаа чавх барьсан бяцхан хүү ч биш. Зүгээр л дэгдээхэйнүүдийн зузаан руу асар том их бууны сум нисдэг. Яг орон нутгийн дүрэмтодорхойгүй байгаа хязгаарыг шийдвэрлэх эсвэл .

L'Hopital-ийн дүрэм бол эдгээр эргэлзээг хурдан бөгөөд үр дүнтэй арилгах боломжийг олгодог маш хүчирхэг арга бөгөөд асуудлын цуглуулгад, хяналтын ажил, офсет, тогтвортой тамга ихэвчлэн олддог: "хязгаарыг тооцоолох, L'Hopital-ийн дүрмийг ашиглахгүйгээр". Зоригтой шаардлага байж болно цэвэр ухамсароноож, ямар ч хичээлийн хязгаарт Хязгаарлалт. Шийдлийн жишээ, Сонирхолтой хязгаарууд. Шийдвэрлэх аргуудыг хязгаарлах, Гайхалтай тэнцэл, "тэгээс тэг" эсвэл "хязгааргүйгээс хязгааргүй" тодорхойгүй байдал үүсдэг. Даалгаврыг товчхон томъёолсон ч гэсэн - "хязгаарыг тооцоолох" бол та L'Hospital-ийн дүрмийг биш харин дуртай зүйлээ ашиглах болно гэдгийг далдаар ойлгодог.

Нийтдээ хоёр дүрэм байдаг бөгөөд тэдгээр нь мөн чанараараа ч, хэрэглэх арга барилаараа ч хоорондоо маш төстэй юм. Сэдвийн талаархи шууд жишээнүүдээс гадна бид судлах болно нэмэлт материал, энэ нь математик анализыг цаашид судлах явцад хэрэг болно.

Дүрмүүдийг товч "практик" хэлбэрээр өгөх болно гэдгийг би даруй анхааруулах бөгөөд хэрэв та онолыг давах шаардлагатай бол илүү нарийвчлалтай тооцоолол хийхийн тулд сурах бичигт хандахыг зөвлөж байна.

L'Hospital-ийн анхны дүрэм

Үүний функцуудыг авч үзье хязгааргүй жижигхэзээ нэгэн цагт. Хэрэв тэдний харилцаанд хязгаарлалт байгаа бол тодорхойгүй байдлыг арилгахын тулд бид үүнийг авч болно хоёр деривативууд- тоологч болон хуваагчаас. Үүнд: , тэр бол .

Анхаарна уу : хязгаар нь бас байх ёстой, эс тэгвээс дүрэм үйлчлэхгүй.

Дээрхээс юу гарах вэ?

Эхлээд та олох чадвартай байх хэрэгтэй функцүүдийн деривативуудМөн сайн байх тусмаа сайн =)

Хоёрдугаарт, деривативуудыг тоологчоос ТУСДАА, хуваагчаас тусад нь авна. Хэмжилтийг ялгах дүрэмтэй андуурч болохгүй !!!

Гуравдугаарт, "х" нь хаана ч, тэр дундаа хязгааргүй байдалд чиглэж болно - хэрэв зөвхөн тодорхойгүй байдал байсан бол.

Эхний өгүүллийн 5-р жишээ рүү буцъя хязгаарлалтын тухай, энэ нь дараах үр дүнд хүргэсэн:

Тодорхойгүй байдал 0:0 бол бид L'Hospital-ийн эхний дүрмийг хэрэгжүүлдэг:

Таны харж байгаагаар тоологч ба хуваагчийг ялгах нь биднийг хагас эргэлтээр хариулт руу хөтөлсөн: бид "хоёр" гэж орлуулсан хоёр энгийн деривативыг олсон бөгөөд тодорхойгүй байдал ул мөргүй алга болсон юм!

L'Hopital-ийн дүрмийг хоёр ба түүнээс дээш удаа дараалан хэрэглэх нь ердийн зүйл биш юм (энэ нь хоёр дахь дүрэмд мөн хамаарна). Үүнийг чимэг үдшийн жишээ 2 хичээлээр гаргая гайхалтай хязгааруудын тухай:

Дээр давхар орхоёр уут дахин хөргөнө. L'Hospital-ийн дүрмийг хэрэгжүүлье:

Эхний алхамд хуваагчийг авдаг болохыг анхаарна уу нийлмэл функцийн дериватив. Үүний дараа бид хэд хэдэн завсрын хялбаршуулалтыг хийж, ялангуяа косинусаас салж, энэ нь нэгдмэл байх хандлагатай байгааг харуулж байна. Тодорхой бус байдлыг арилгаагүй тул бид L'Hopital дүрмийг дахин хэрэглэнэ (хоёр дахь мөр).

Би танд зориулж бага зэрэг өөрийгөө шалгах жишээг сонгоогүй. Тэд хэрхэн олдсон нь бүрэн тодорхойгүй бол деривативууд, та ялгах техникээ бэхжүүлэх хэрэгтэй, хэрэв та косинусын заль мэхийг ойлгохгүй байвал буцаж очно уу гайхалтай хязгаарууд. би олж харахгүй байна онцгой утгаБи дериватив болон хязгаарлалтын талаар хангалттай дэлгэрэнгүй ярьсан тул алхам алхмаар тайлбар дээр. Өгүүллийн шинэлэг зүйл нь дүрмүүд болон зарим техникийн шийдлүүдэд оршдог.

Өмнө дурьдсанчлан, ихэнх тохиолдолд L'Hopital дүрмийг ашиглах шаардлагагүй боловч шийдлийг бүдүүлэг шалгахын тулд тэдгээрийг ашиглахыг зөвлөж байна. Ихэнхдээ, гэхдээ үргэлж биш. Тиймээс, жишээлбэл, ашигласан жишээг шалгах нь илүү ашигтай байдаг гайхалтай тэнцэл.

L'Hospital-ийн хоёр дахь дүрэм

Ах-2 унтаж байгаа хоёр наймтай тулалддаг. Үүнтэй адилаар:

Хэрэв харилцааны хязгаар байгаа бол хязгааргүй томфункцийн цэг дээр: , дараа нь тодорхойгүй байдлыг арилгахын тулд бид авч болно хоёр дериватив– Тоологчоос ТУС, хуваагчаас ТУСЛА. Үүнд: , тэр бол тоологч ба хуваагчийг ялгах үед хязгаарын утга өөрчлөгдөхгүй.

Анхаарна уу : хязгаар байх ёстой

Дахин хэлэхэд янз бүрийн хэлбэрээр практик жишээнүүд үнэ цэнэ өөр байж болно, үүнд хязгааргүй. Тодорхой бус байдал байх нь чухал.

Эхний хичээлийн 3-р жишээг шалгая: . Бид L'Hospital-ийн хоёр дахь дүрмийг ашигладаг:

Бид аваргуудын тухай ярьж байгаа тул хоёр каноник хязгаарыг шинжлэх болно.

Жишээ 1

Хязгаарыг тооцоолох

"Ердийн" аргаар хариулт авах нь тийм ч хялбар биш тул "хязгааргүйгээс хязгааргүй" тодорхойгүй байдлыг илрүүлэхийн тулд бид L'Hopital дүрмийг ашигладаг.

Энэ замаар, шугаман функцнэгээс их суурьтай логарифмаас илүү өсөлтийн дараалал(гэх мэт). Мэдээжийн хэрэг, дээд зэрэглэлийн "x" нь ийм логарифмуудыг "татах" болно. Үнэн хэрэгтээ, функц нь нэлээд удаан ургадаг бөгөөд түүний хуваарьижил "x" -тэй харьцуулахад илүү зөөлөн байдаг.

Жишээ 2

Хязгаарыг тооцоолох

Өөр нэг бүдгэрсэн хүрээ. Тодорхой бус байдлыг арилгахын тулд бид L'Hopital дүрмийг дараалан хоёр удаа ашигладаг.

Экспоненциал функц, нэгээс их суурьтай(гэх мэт) -аас өндөр өсөлтийн дараалал эрчим хүчний функцэерэг зэрэгтэй.

Энэ хугацаанд ижил төстэй хязгаарлалтууд тулгардаг бүрэн функциональ судалгаа, тухайлбал, олох үед графикийн асимптот. Тэд мөн дээрх зарим даалгавар дээр харагдаж байна магадлалын онол. Үзүүлсэн хоёр жишээг анхаарч үзэхийг би танд зөвлөж байна, энэ нь тоологч ба хуваагчийг ялгахаас илүү сайн зүйл байхгүй цөөхөн тохиолдлын нэг юм.

Цаашид бичвэрт би L'Hopital-ийн эхний болон хоёр дахь дүрмийг ялгахгүй, энэ нь зөвхөн нийтлэлийг зохион байгуулах зорилгоор хийгдсэн болно. Ер нь миний бодлоор математикийн аксиом, теорем, дүрэм, шинж чанарыг хэтрүүлэн тоолох нь бага зэрэг хор хөнөөлтэй, учир нь "Теорем 19-ийн дагуу 3-р дүгнэлтийн дагуу ..." гэх мэт хэллэгүүд зөвхөн нэг зүйлийн хүрээнд мэдээлэлтэй байдаг. эсвэл өөр сурах бичиг. Мэдээллийн өөр эх сурвалжид мөн адил "үр дүн 2 ба теорем 3" байх болно. Ийм мэдэгдэл нь зөвхөн зохиогчдын хувьд албан ёсны бөгөөд тохиромжтой байдаг. Математикийн баримтын мөн чанарыг дурдах нь дээр. Үл хамаарах зүйл бол түүхэн тогтсон нэр томъёо юм, жишээлбэл, анхны гайхалтай хязгаарэсвэл хоёр дахь гайхалтай хязгаар.

Парисын Шинжлэх Ухааны Академийн гишүүн Маркиз Гийом Франсуа де Лопиталын тавьсан сэдвийг бид үргэлжлүүлэн хөгжүүлсээр байна. Нийтлэл нь тодорхой практик будгийг олж авдаг бөгөөд нэлээд нийтлэг ажилд дараахь зүйлийг шаарддаг.

Дулаацахын тулд хэд хэдэн жижиг бор шувуутай харьцъя:

Жишээ 3

Косинусыг арилгах замаар хязгаарыг урьдчилан хялбаршуулж болох боловч бид нөхцөлийг хүндэтгэж, тоологч ба хуваагчийг нэн даруй ялгах болно.

Деривативыг олох явцад стандарт бус зүйл байдаггүй, жишээлбэл, ердийн хуваагчийг ашигладаг. ялгах дүрэмажилладаг .

Үзсэн жишээ нь устгагдаж, дамждаг гайхалтай хязгаарууд, ижил төстэй тохиолдлыг өгүүллийн төгсгөлд авч үзсэн болно Цогцолбор хязгаар.

Жишээ 4

L'Hopital-ийн дүрмийн дагуу хязгаарыг тооцоол

Энэ бол жишээ юм бие даасан шийдвэр. Сайхан онигоо =)

Ердийн нөхцөл байдал бол ялгасны дараа гурван эсвэл дөрвөн давхар бутархайг олж авах явдал юм.

Жишээ 5

L'Hospital-ийн дүрмийг ашиглан хязгаарыг тооцоол

Өргөдөл гаргахыг гуйж байна гайхалтай тэнцэл, гэхдээ зам нь нөхцөлөөр хатуу кодлогдсон байна:

Ялгаварсны дараа би олон давхар фракцаас салж, хамгийн их хялбаршуулахыг зөвлөж байна.. Мэдээжийн хэрэг, ахисан түвшний оюутнууд алгасаж болно сүүлчийн алхамТэгээд тэр даруй бичнэ үү: , гэхдээ зарим хязгаарт онц сайн оюутнууд ч төөрөлдөх болно.

Жишээ 6

L'Hospital-ийн дүрмийг ашиглан хязгаарыг тооцоол

Жишээ 7

L'Hospital-ийн дүрмийг ашиглан хязгаарыг тооцоол

Эдгээр нь өөртөө туслах жишээ юм. Жишээ 7-д та юуг ч хялбарчилж чадахгүй, бутархайг ялгасны дараа хэтэрхий энгийн болж хувирна. Гэхдээ 8-р жишээнд L'Hopital дүрмийг хэрэглэсний дараа тооцоолол нь хамгийн тохиромжтой биш тул гурван давхар байгууламжаас салах нь зүйтэй юм. Бүрэн шийдэлмөн хичээлийн төгсгөлд хариулт. Хэрэв танд ямар нэгэн асуудал байгаа бол - тригонометрийн хүснэгттуслах.

Мөн ялгавартай байдлын дараа тодорхойгүй байдал үүссэн тохиолдолд хялбаршуулах нь зайлшгүй шаардлагатай арилгаагүй.

Жишээ 8

L'Hospital-ийн дүрмийг ашиглан хязгаарыг тооцоол

Явах:

Сонирхолтой нь, анхны ялгааны дараах анхны тодорхойгүй байдал нь тодорхойгүй байдал болж хувирсан бөгөөд L'Hôpital-ийн дүрмийг цаашид ч үл тоомсорлодог. Мөн "ойлт" болгоны дараа дөрвөн давхар бутархайг хэрхэн арилгаж, тогтмолуудыг хязгаарын тэмдэгээс гаргаж байгааг анхаарна уу. Илүү их энгийн жишээнүүдТогтмол тоонуудыг гаргахгүй байх нь илүү тохиромжтой, гэхдээ хязгаар нь нарийн төвөгтэй үед бид бүх зүйлийг-бүх зүйлийг-бүх зүйлийг хялбаршуулдаг. Шийдвэрлэсэн жишээний заль мэх нь бас хэзээд байдагт оршино , гэхдээ иймээс синусыг арилгах явцад шинж тэмдгүүдэд эргэлзэх нь гайхмаар зүйл биш юм. Эцсийн шатанд синусыг устгах боломжгүй байсан ч жишээ нь нэлээд хүнд, уучлагдах боломжтой юм.

Нөгөө өдөр би нэгэн сонирхолтой даалгавартай таарав:

Жишээ 9

Үнэнийг хэлэхэд, энэ хязгаар нь юутай тэнцэх вэ гэдэгт би бага зэрэг эргэлзэж байсан. Дээр дурдсанчлан "x" нь илүү байна өндөр захиалгаөсөлт нь логарифмаас илүү, гэхдээ энэ нь куб логарифмаас илүү байх уу? Хэн ялахыг өөрөө олж мэдэхийг хичээгээрэй.

Тийм ээ, L'Hopital-ийн дүрэм бол бор шувуу руу их буугаар буудах төдийгүй шаргуу хөдөлмөр юм ....

L'Hôpital-ийн дүрмийг уут эсвэл ядарсан наймуудад хэрэглэхийн тулд маягтын тодорхой бус байдлыг багасгадаг.

Тодорхой бус байдлыг шийдвэрлэх талаар хичээлийн 9-13 дугаар жишээнд дэлгэрэнгүй авч үзсэн болно. Шийдвэрлэх аргуудыг хязгаарлах. Үүний тулд өөр нэгийг авъя:

Жишээ 10

L'Hopital-ийн дүрмийг ашиглан функцийн хязгаарыг тооцоол

Эхний алхамд бид илэрхийлэлийг өгдөг Ерөнхий хуваарь, ингэснээр тодорхойгүй байдлыг тодорхойгүй байдал болгон хувиргадаг. Дараа нь бид L'Hopital дүрмийг дагаж мөрддөг:

Энд дашрамд хэлэхэд дөрвөн давхар илэрхийлэлд хүрэх нь утгагүй тохиолдол юм.

Тодорхойгүй байдал нь дараах болон хувирахыг эсэргүүцдэггүй.

Жишээ 11

L'Hopital-ийн дүрмийг ашиглан функцийн хязгаарыг тооцоол

Энд байгаа хязгаар нь нэг талыг барьсан бөгөөд ийм хязгаарлалтыг гарын авлагад аль хэдийн авч үзсэн болно Функцийн график ба шинж чанарууд. Таны санаж байгаагаар "сонгодог" логарифмын график тэнхлэгийн зүүн талд байхгүй тул бид зөвхөн баруун талаас тэг рүү ойртож чадна.

L'Hôpital-ийн нэг талын хязгаарлалтын дүрмүүд ажилладаг боловч тодорхой бус байдлыг эхлээд шийдвэрлэх хэрэгтэй. Эхний алхамд бид тодорхойгүй байдлыг олж авсан бутархайг гурван давхар болгож, дараа нь загвар схемийн дагуу шийдэл гарна.

Тоолуур ба хуваагчийг ялгаж авсны дараа бид хялбарчлахын тулд дөрвөн давхар бутархайгаас ангижрах болно. Үүний үр дүнд тодорхойгүй байдал үүссэн. Бид заль мэхийг давтан хэлье: бид дахин бутархайг гурван давхар болгож, үүссэн тодорхойгүй байдалд L'Hopital дүрмийг дахин хэрэглэнэ.

Бэлэн.

Анхны хязгаарҮүнийг хоёр гурилан бүтээгдэхүүн болгон багасгахыг оролдож болно:

Гэхдээ нэгдүгээрт, хуваагч дахь дериватив нь илүү хэцүү, хоёрдугаарт, үүнээс сайн зүйл гарахгүй.

Энэ замаар, ижил төстэй жишээг шийдэхийн өмнө та дүн шинжилгээ хийх хэрэгтэй(амаар эсвэл ноорог дээр) ЯМАР тодорхойгүй байдлыг бууруулах нь илүү ашигтай вэ - "тэгээс тэг" эсвэл "хязгааргүйгээс хязгааргүй" хүртэл.

Хариуд нь архи уудаг хамтрагчид болон илүү чамин нөхдүүд гэрэл рүү татагддаг. Өөрчлөлтийн арга нь энгийн бөгөөд стандарт юм.

Шийдэл онлайн функцийн хязгаарлалт. Нэг цэг дэх функц эсвэл функциональ дарааллын хязгаарын утгыг олох, тооцоол хязгаарлаххязгааргүй дэх функцийн утга. тооны цувралын нийлэлтийг тодорхойлох ба бидний ачаар илүү их зүйлийг хийж болно онлайн үйлчилгээ- . Бид танд функцийн хязгаарыг онлайнаар хурдан бөгөөд үнэн зөв олох боломжийг олгодог. Та өөрөө орно функцийн хувьсагчХүсч буй хязгаарын хувьд манай үйлчилгээ таны төлөө бүх тооцоог хийж, үнэн зөв бөгөөд энгийн хариултыг өгдөг. Мөн төлөө хязгаарыг онлайнаар олохта тоон цуврал болон хоёуланг нь оруулж болно аналитик функцууд, шууд илэрхийлэлд тогтмолуудыг агуулсан. Энэ тохиолдолд олсон функцийн хязгаар нь эдгээр тогтмолуудыг илэрхийлэлд тогтмол аргумент болгон агуулна. Манай үйлчилгээ аливаа асуудлыг шийддэг сорилттой даалгаваруудбайршлаар онлайн хязгаарлалт, энэ нь функц болон тооцоолох шаардлагатай цэгийг зааж өгөхөд хангалттай функцийн хязгаар. Тооцоолох онлайн хязгаарлалт, та ашиглаж болно янз бүрийн аргаүр дүнг харьцуулахдаа тэдгээрийг шийдвэрлэх дүрмүүд шийдлийг онлайнаар хязгаарлах www.site дээр, энэ нь даалгаврыг амжилттай дуусгахад хүргэнэ - та өөрийн алдаа, үсгийн алдаанаас зайлсхийх болно. Эсвэл та функцийн хязгаарын бие даасан тооцоололд нэмэлт хүчин чармайлт, цаг зарцуулахгүйгээр бидэнд бүрэн итгэж, бидний үр дүнг ажилдаа ашиглах боломжтой. Бид хязгааргүй гэх мэт хязгаарын утгыг оруулахыг зөвшөөрдөг. Та нийтлэг нэр томъёог оруулах ёстой тооны дараалалболон www.siteутгыг тооцох болно онлайнаар хязгаарлахнэмэх эсвэл хасах хязгааргүй.

Математик анализын үндсэн ойлголтуудын нэг нь функцийн хязгаарболон дарааллын хязгаарнэг цэгт болон хязгааргүй үед зөв шийдэж чаддаг байх нь чухал хязгаар. Манай үйлчилгээгээр энэ нь тийм ч хэцүү биш байх болно. Шийдвэр гарч байна онлайн хязгаарлалтсекундын дотор хариулт үнэн зөв, бүрэн гүйцэд байна. Тооцооллын судалгаа нь үүнээс эхэлдэг хязгаарт хүрэх, хязгаарДээд математикийн бараг бүх хэсэгт ашиглагддаг тул сервертэй байх нь ашигтай байдаг шийдлийг онлайнаар хязгаарлахаль сайт вэ.

0/0 эсвэл ∞/∞ хэлбэрийн тодорхойгүй байдал болон тооцоололд үүссэн бусад тодорхой бус байдлын тодруулга хязгаархязгааргүй жижиг буюу хязгааргүй хоёрын харьцаа том функцууд L'Hospital-ийн дүрмийн тусламжтайгаар маш хялбаршуулсан (үнэндээ хоёр дүрэм, тэдгээрийн талаархи тайлбар).

мөн чанар L'Hospital-ийн дүрэм Хязгааргүй жижиг эсвэл хязгааргүй том хоёр функцийн харьцааны хязгаарыг тооцоолоход 0/0 эсвэл ∞/∞ хэлбэрийн тодорхойгүй байдал гарсан тохиолдолд хоёр функцийн харьцааны хязгаарыг 2-ын хязгаараар сольж болно. тэдгээрийн харьцаа деривативуудулмаар тодорхой үр дүнд хүрнэ.

L'Hopital-ийн дүрмийн томъёолол руу шилжье.

Хязгааргүй жижиг хоёр утгын хязгаарын тухай Л'Хопиталын дүрэм. Хэрэв функцууд е(x) ба g(x аа, мөн энэ хороололд g"(x ахоорондоо тэнцүү ба тэгтэй тэнцүү

().

Хязгааргүй их хоёр хэмжигдэхүүний хязгаарын тухай Л'Хопиталын дүрэм. Хэрэв функцууд е(x) ба g(x) нь тухайн цэгийн зарим хэсэгт ялгаатай байдаг а, боломжит цэгийг эс тооцвол а, мөн энэ хороололд g"(x)≠0 ба хэрэв эдгээр функцүүдийн хязгаарууд нь тухайн цэг дээрх функцийн утга руу чиглэнэ. ахоорондоо тэнцүү ба хязгааргүйтэй тэнцүү

(),

тэгвэл эдгээр функцүүдийн харьцааны хязгаар нь тэдгээрийн деривативуудын харьцааны хязгаартай тэнцүү байна

().

Өөрөөр хэлбэл, 0/0 эсвэл ∞/∞ хэлбэрийн тодорхойгүй байдлын хувьд хоёр функцийн харьцааны хязгаар нь хэрэв сүүлийнх нь байгаа бол тэдгээрийн деривативуудын харьцааны хязгаартай тэнцүү байна (хязгааргүй эсвэл хязгааргүй).

Тайлбар.

1. Функц ажиллах үед L'Hopital-ийн дүрэм мөн хамаарна е(x) ба g(x)-д тодорхойлогдоогүй x = а.

2. Хэрэв функцын деривативын харьцааны хязгаарыг тооцохдоо е(x) ба g(x) бид дахин 0/0 эсвэл ∞/∞ хэлбэрийн тодорхойгүй байдалд хүрвэл L'Hopital-ийн дүрмийг дахин дахин (дор хаяж хоёр удаа) хэрэглэх ёстой.

3. (x) функцын аргумент нь төгсгөлгүй тоо руу чиглэх үед L'Hopital-ийн дүрэм мөн хамаарна. а, мөн хязгааргүй хүртэл ( x → ∞).

Бусад төрлийн тодорхойгүй байдлыг мөн 0/0 ба ∞/∞ төрлийн тодорхойгүй байдал болгон бууруулж болно.

"Тэгийг тэгээр хуваасан", "хязгааргүйг хязгааргүй хуваасан" төрлийн тодорхойгүй байдлын тодруулга.

Жишээ 1

x=2 нь 0/0 хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс функц бүрийн дериватив ба бид авна

Тоолуур дээр олон гишүүнтийн деривативыг тооцоолж, хуваагч дээр - нийлмэл логарифм функцийн дериватив. Сүүлчийн тэнцүү тэмдгийн өмнө ердийн хязгаар, x-ийн оронд deuce-г орлуулах.

Жишээ 2 L'Hospital-ийн дүрмийг ашиглан хоёр функцийн харьцааны хязгаарыг тооцоол.

Шийдэл. Орлуулах өгөгдсөн функцүнэт зүйлс x

Жишээ 3 L'Hospital-ийн дүрмийг ашиглан хоёр функцийн харьцааны хязгаарыг тооцоол.

Шийдэл. Өгөгдсөн утгын функцэд орлуулах x=0 нь 0/0 хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид тоологч ба хуваагч дахь функцүүдийн деривативуудыг тооцоод дараахь зүйлийг авна.

Жишээ 4Тооцоол

Шийдэл. Өгөгдсөн функцэд х-ийн утгыг нэмэх хязгаартай тэнцүү болгох нь ∞/∞ хэлбэрийн тодорхойгүй байдалд хүргэдэг. Тиймээс бид L'Hopital-ийн дүрмийг баримтална:

Сэтгэгдэл. Эхний деривативуудын харьцааны хязгаар нь хэлбэрийн тодорхой бус байдал тул L'Hopital дүрмийг хоёр удаа хэрэглэх, өөрөөр хэлбэл хоёр дахь деривативуудын харьцааны хязгаарт хүрэх жишээнүүд рүү шилжье. 0/0 эсвэл ∞/∞.

L'Hopital-ийн дүрмийг өөрөө хэрэгжүүлээд дараа нь шийдлийг хараарай

"Тэгийг хязгааргүй үржүүлсэн" хэлбэрийн тодорхойгүй байдлын тодруулга

Жишээ 12.Тооцоол

.

Шийдэл. Бид авдаг

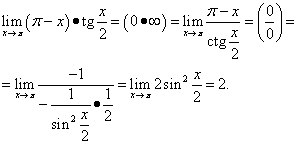
Энэ жишээнд тригонометрийн таних тэмдэг ашигладаг.

"Тэгээс тэг хүртэл", "хязгааргүй нь тэгтэй тэнцүү", "хязгааргүй байдлын нэг" гэсэн төрлүүдийн тодорхойгүй байдлын тодруулга.

Маягтын тодорхойгүй байдал , эсвэл ихэвчлэн 0/0 эсвэл ∞/∞ хэлбэрийн функцийн логарифмыг ашиглан багасгадаг.

Илэрхийллийн хязгаарыг тооцоолохын тулд логарифмын ижил төстэй байдлыг ашиглах хэрэгтэй бөгөөд үүний онцгой тохиолдол нь логарифмын өмч юм. .

Функцийн логарифмын ижилсэл ба тасралтгүй байдлын шинж чанарыг ашиглан (хязгаарын тэмдгээс давахын тулд) хязгаарыг дараах байдлаар тооцоолно.

Тус тусад нь экспонент дахь илэрхийллийн хязгаарыг олж, бүтээх хэрэгтэй долсон хэмжээнд хүртэл.

Жишээ 13

Шийдэл. Бид авдаг

.

.

Жишээ 14 L'Hopital-ийн дүрмийг ашиглан тооцоол

Шийдэл. Бид авдаг

Экспонент дахь илэрхийллийн хязгаарыг тооцоол

.

.

Жишээ 15 L'Hopital-ийн дүрмийг ашиглан тооцоол

Дүрэм гэж хэлсэн бол функцууд е(x) ба g(x) дараах нөхцлүүдтэй байна:

тэгээд байна . Түүгээр ч барахгүй теорем нь бусад суурийн хувьд ч үнэн (заасан үндэслэлд нотолгоог өгөх болно).

Өгүүллэг

Энэ төрлийн тодорхойгүй байдлыг илчлэх аргыг Лопитал онд хэвлэгдсэн "Хязгааргүй жижиг тоонуудын шинжилгээ" бүтээлдээ нийтлүүлсэн. Энэ бүтээлийнхээ оршилд Лопитал Лейбниц болон ах дүү Бернулли нарын нээлтийг ямар ч эргэлзээгүйгээр ашигласан бөгөөд "Тэд хүссэн зүйлдээ зохиогчийн эрхээ харуулахын эсрэг юу ч байхгүй" гэж онцолжээ. Иоганн Бернулли L'Hospital-ийн бүх ажлыг нэхэмжилсэн бөгөөд ялангуяа L'Hospital нас барсны дараа тэрээр "Бутархай, хуваагч, хуваарийн утгыг тодорхойлох Infinitesimal Analysis-д хэвлэгдсэн миний аргын сайжруулалт" гэсэн гайхалтай гарчигтай бүтээлээ хэвлүүлсэн. заримдаа алга болдог", .

Баталгаа

Хязгааргүй жижиг тоонуудын харьцаа

Функцуудын хязгаар тэгтэй тэнцүү байх (хэлбэрийн тодорхойгүй байдал гэж нэрлэгддэг) тохиолдолд теоремыг баталъя.

Учир нь бид функцуудыг харж байна еболон gзөвхөн цэгийн баруун цоорсон хагас хороололд а, бид энэ үед тэдгээрийг тасралтгүй дахин тодорхойлж болно: let е(а) = g(а) = 0 . Заримыг нь авцгаая xавч үзэж буй хагас хөршөөс авч, сегментэд Коши теоремыг хэрэглэнэ. Энэ теоремоор бид дараахь зүйлийг олж авна.

,

гэхдээ е(а) = g(а) = 0 , ийм учраас .

Төгсгөлийн хязгаарын хувьд src="/pictures/wiki/files/56/85e2b8bb13d6fb1ddcf88e22a4bb6ef2.png" border="0"> болон src="/pictures/wiki/files/101/e8b2f2b8861947c812f2b8861947c812f2b8861947c812f2b8861947c81200"6find. ,

Энэ нь функцүүдийн харьцааны хязгаарын тодорхойлолт юм.

Хязгааргүй том харьцаа

Хэлбэрийн тодорхойгүй байдлын теоремыг баталъя.

Эхлэхийн тулд деривативын харьцааны хязгаарыг төгсгөлтэй ба тэнцүү гэж үзье А. Тэгээд хичээж байхдаа xруу абаруун талд энэ хамаарлыг дараах байдлаар бичиж болно А+ α , энд α - (1). Энэ нөхцлийг бичье:

.

Засацгаая тсегментээс аваад Коши теоремыг бүгдэд нь хэрэглэнэ xсегментээс:

, үүнийг дараах хэлбэрт оруулж болно. .

Учир нь x, хангалттай ойрхон байна а, илэрхийлэл нь утга учиртай; баруун талын эхний хүчин зүйлийн хязгаар нь нэгтэй тэнцүү байна (учир нь е(т) ба g(т) нь тогтмол ба е(x) ба g(x) хязгааргүй байх хандлагатай байдаг). Иймээс энэ хүчин зүйл нь 1 + β-тэй тэнцүү бөгөөд энд β нь хязгааргүй жижиг функц юм. xруу абаруун талд. Бид α-ийн тодорхойлолттой ижил утгыг ашиглан энэ баримтын тодорхойлолтыг бичнэ.

.

Функцуудын харьцааг (1 + β) хэлбэрээр илэрхийлж болохыг бид олж мэдсэн. А+ α) , ба . Өгөгдсөн аль нэгийн хувьд функцүүдийн харьцаа хоорондын зөрүүгийн модулийг олж болно Абага байсан нь функцүүдийн харьцааны хязгаар нь үнэхээр тэнцүү байна гэсэн үг юм А .

Хэрэв хязгаар бол Ахязгааргүй (үүнийг нэмэх хязгаартай тэнцүү гэж үзье), тэгвэл

(x))(g"(x))>2M)" src="/pictures/wiki/files/101/e46c5113c49712376d1c357b5b202a65.png" border="0">.

β-ийн тодорхойлолтод бид авна; баруун талын эхний хүчин зүйл нь 1/2-ээс их байх болно x, хангалттай ойрхон байна а, дараа нь src="/pictures/wiki/files/50/2f7ced4a9b4b06f7b9085e982250dbcf.png" border="0">.

Бусад үндэслэлүүдийн хувьд нотлох баримтууд нь өгөгдсөнтэй төстэй байна.

Жишээ

(Зөвхөн тоологч ба хуваагч BOTH нь 0 ; эсвэл ; эсвэл .

Викимедиа сан. 2010 он.

Бусад толь бичгүүдээс "L'Hopital дүрэм" гэж юу болохыг хараарай:

Тодорхой бус байдлыг илчлэх үндсэн дүрмүүдийн нэг нь түүхэн буруу нэр. L. p.-г I. Bernoulli олж, 1696 онд энэ дүрмийг нийтэлсэн G. L'Hopital-д мэдээлсэн (L'Hopital-ыг үзнэ үү). Тодорхойгүй илэрхийлэлүүдийг үзнэ үү ... Зөвлөлтийн агуу нэвтэрхий толь бичиг

Функцийн харьцааны хязгаарыг авч үзэж буй функцүүдийн деривативын харьцааны хязгаарт бууруулах замаар хэлбэрийн тодорхойгүй байдлыг тодруулах. Тэгэхээр, бодит функц f ба g нь тоон цэгийн баруун гар талын цоорхойд тодорхойлогдсон тохиолдолд ... ... Математик нэвтэрхий толь бичиг

Bernoulli L'Hospital-ийн дүрэм нь u хэлбэрийн тодорхойгүй байдлыг илрүүлэх функцүүдийн хязгаарыг олох арга юм. Аргыг зөвтгөх теорем нь тодорхой нөхцөлд функцүүдийн харьцааны хязгаар нь тэдгээрийн деривативуудын харьцааны хязгаартай тэнцүү байна ... ... Википедиа

AT математик шинжилгээ L'Hopital-ийн дүрэм нь функцүүдийн хязгаарыг олох, 0/0 ба хэлбэрийн тодорхойгүй байдлыг илрүүлэх арга юм. Аргыг зөвтгөх теорем нь тодорхой нөхцөлд функцүүдийн харьцааны хязгаар нь хязгаартай тэнцүү байна ... ... Википедиа

Математик анализын хувьд L'Hopital-ийн дүрэм нь функцүүдийн хязгаарыг олох, 0/0 ба хэлбэрийн тодорхойгүй байдлыг илрүүлэх арга юм. Аргыг зөвтгөх теорем нь тодорхой нөхцөлд функцүүдийн харьцааны хязгаар нь хязгаартай тэнцүү байна ... ... Википедиа