Санамсаргүй хэмжигдэхүүний тархалтын хууль нь математикийн хүлээлтийг олох явдал юм. Дискрет санамсаргүй хэмжигдэхүүн. дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль
1-р бүлэг. Дискрет санамсаргүй утга
§ 1. Санамсаргүй хэмжигдэхүүний тухай ойлголтууд.
Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль.
Тодорхойлолт : Санамсаргүй хэмжигдэхүүн нь туршилтын үр дүнд өөрийн боломжит багц утгуудаас зөвхөн нэг утгыг авдаг, урьдчилан мэдэгддэггүй, санамсаргүй шалтгаанаас хамаарна.
Санамсаргүй хэмжигдэхүүн нь дискрет ба тасралтгүй гэсэн хоёр төрөлтэй.
Тодорхойлолт : Х санамсаргүй хэмжигдэхүүнийг дуудна салангид (тасралттай) хэрэв түүний утгуудын багц нь хязгаарлагдмал эсвэл хязгааргүй, гэхдээ тоолж болно.
Өөрөөр хэлбэл, салангид санамсаргүй хэмжигдэхүүний боломжит утгуудыг дахин дугаарлаж болно.
Санамсаргүй хэмжигдэхүүнийг тархалтын хуулийг ашиглан тодорхойлж болно.
Тодорхойлолт : Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль санамсаргүй хэмжигдэхүүний боломжит утгууд ба тэдгээрийн магадлалын хоорондох захидал харилцааг нэрлэнэ.
Дискрет санамсаргүй хэмжигдэхүүн X-ийн тархалтын хуулийг хүснэгт хэлбэрээр зааж өгч болох бөгөөд эхний мөрөнд санамсаргүй хэмжигдэхүүний бүх боломжит утгыг өсөх дарааллаар, хоёр дахь мөрөнд эдгээрийн харгалзах магадлалыг зааж өгсөн болно. үнэт зүйлс, жишээлбэл.
Энд р1+ р2+…+ рn=1
Ийм хүснэгтийг салангид санамсаргүй хэмжигдэхүүний тархалтын цуваа гэж нэрлэдэг.
Хэрэв санамсаргүй хэмжигдэхүүний боломжит утгуудын багц хязгааргүй бол p1+ p2+…+ pn+… цуврал нийлж, нийлбэр нь 1-тэй тэнцүү байна.
Дискрет санамсаргүй хэмжигдэхүүн X-ийн тархалтын хуулийг графикаар дүрсэлж болно тэгш өнцөгт системкоординатууд (xi; pi), i=1,2,...n-тэй цэгүүдийг дараалан холбосон полилинийг байгуулна. Үүссэн мөрийг дуудна түгээлтийн полигон (Зураг 1).
Органик хими" href="/text/category/organicheskaya_hiimya/" rel="bookmark">органик хими тус тус 0.7 ба 0.8 байна. Х санамсаргүй хэмжигдэхүүн - оюутны тэнцэх шалгалтын тоог хуваарилах хуулийг гарга.
Шийдэл. Шалгалтын үр дүнд тооцсон санамсаргүй хэмжигдэхүүн X нь дараах утгуудын аль нэгийг авч болно: x1=0, x2=1, x3=2.
Эдгээр утгуудын магадлалыг олцгооё: Үйл явдлыг тэмдэглэе.
https://pandia.ru/text/78/455/images/image004_81.jpg" өргөн "259" өндөр "66 src=">
 |
Тиймээс X санамсаргүй хэмжигдэхүүний тархалтын хуулийг хүснэгтээр өгөв.
Хяналт: 0.6+0.38+0.56=1.
§ 2. Түгээлтийн функц
Санамсаргүй хэмжигдэхүүний бүрэн тодорхойлолтыг мөн тархалтын функцээр өгдөг.
Тодорхойлолт: Х дискрет санамсаргүй хэмжигдэхүүний тархалтын функц X санамсаргүй хэмжигдэхүүн нь x-ээс бага утгыг авах магадлалыг x утга тус бүрээр тодорхойлдог F(x) функц гэж нэрлэдэг.
F(x)=P(X<х)
Геометрийн хувьд тархалтын функцийг санамсаргүй хэмжигдэхүүн X нь х цэгийн зүүн талд байрлах цэгээр тоон шулуун дээр дүрслэгдсэн утгыг авах магадлал гэж тайлбарладаг.
1)0≤ F(x) ≤1;
2) F(x) нь (-∞;+∞) дээр буурахгүй функц;
3) F(x) - x= xi (i=1,2,...n) цэгүүдэд зүүн талдаа үргэлжилсэн, бусад бүх цэгүүдэд тасралтгүй;
4) F(-∞)=P (X<-∞)=0 как вероятность невозможного события Х<-∞,
F(+∞)=P(X<+∞)=1 как вероятность достоверного события Х<-∞.
Дискрет санамсаргүй хэмжигдэхүүн X-ийн тархалтын хуулийг хүснэгт хэлбэрээр өгвөл:
Дараа нь F(x) тархалтын функцийг дараах томъёогоор тодорхойлно.
https://pandia.ru/text/78/455/images/image007_76.gif" height="110">
x≤ x1-ийн хувьд 0,
x1 дээр р1< х≤ x2,
F(x)= x2 дээр р1 + р2< х≤ х3
x>xn-д 1.
Түүний графикийг 2-р зурагт үзүүлэв.

§ 3. Дискрет санамсаргүй хэмжигдэхүүний тоон шинж чанар.
Чухал тоон шинж чанарууд орно хүлээгдэж буй үнэ цэнэ.
Тодорхойлолт: Математикийн хүлээлт M(X) Дискрет санамсаргүй хэмжигдэхүүн X нь түүний бүх утгуудын үржвэр ба тэдгээрийн харгалзах магадлалын нийлбэр юм.
М(X) = ∑ xiри= x1р1 + x2р2+…+ xnрn
Математикийн хүлээлт нь санамсаргүй хэмжигдэхүүний дундаж утгын шинж чанар болдог.
Математикийн хүлээлтийн шинж чанарууд:
1)M(C)=C, энд C нь тогтмол утга;
2)M(C X)=C M(X),
3)M(X±Y)=M(X) ±M(Y);
4)M(X Y)=M(X) M(Y), энд X,Y нь бие даасан санамсаргүй хэмжигдэхүүн;
5)M(X±C)=M(X)±C, энд C нь тогтмол утга;
Дискрет санамсаргүй хэмжигдэхүүний боломжит утгуудын дундаж утгын ойролцоо тархалтын түвшинг тодорхойлохын тулд дисперсийг ашигладаг.
Тодорхойлолт: Зөрчил Д ( X ) санамсаргүй хэмжигдэхүүн X нь санамсаргүй хэмжигдэхүүний математик хүлээлтээс квадрат хазайлтын математик хүлээлт юм.
Тархалтын шинж чанарууд:
1)D(C)=0, энд C нь тогтмол утга;
2)D(X)>0, энд X нь санамсаргүй хэмжигдэхүүн;
3)D(C X)=C2 D(X), энд C нь тогтмол утга;
4)D(X+Y)=D(X)+D(Y), энд X,Y нь бие даасан санамсаргүй хэмжигдэхүүн;
Зөрчлийг тооцоолохын тулд дараах томъёог ашиглах нь ихэвчлэн тохиромжтой байдаг.
D(X)=M(X2)-(M(X))2,
Энд M(X)=∑ xi2рi= x12р1 + x22р2+…+ xn2рn
D(X) дисперс нь квадрат санамсаргүй хэмжигдэхүүний хэмжээстэй бөгөөд энэ нь үргэлж тохиромжтой байдаггүй. Тиймээс √D(X) утгыг мөн санамсаргүй хэмжигдэхүүний боломжит утгуудын тархалтын үзүүлэлт болгон ашигладаг.
Тодорхойлолт: Стандарт хэлбэлзэл σ(X) Х санамсаргүй хэмжигдэхүүнийг дисперсийн квадрат язгуур гэнэ.
![]()
Даалгавар №2.Дискрет санамсаргүй хэмжигдэхүүн X нь тархалтын хуулиар тодорхойлогддог.
P2, тархалтын функц F(x)-ийг олоод түүний графикийг мөн M(X), D(X), σ(X)-ийг зур.
Шийдэл: Х санамсаргүй хэмжигдэхүүний боломжит утгуудын магадлалын нийлбэр 1-тэй тэнцүү тул
Р2=1- (0.1+0.3+0.2+0.3)=0.1
F(x)=P(X) тархалтын функцийг олъё Геометрийн хувьд энэ тэгш байдлыг дараах байдлаар тайлбарлаж болно: F(x) нь санамсаргүй хэмжигдэхүүн нь х цэгийн зүүн талд байрлах цэгээр тооны тэнхлэгт дүрслэгдсэн утгыг авах магадлал юм. Хэрэв x≤-1 бол (-∞;x) дээр энэ санамсаргүй хэмжигдэхүүний ганц утга байхгүй тул F(x)=0; Хэрэв -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; Хэрэв 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;x) x1=-1 ба x2=0 гэсэн хоёр утга байна; Хэрэв 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Хэрэв 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Хэрэв x>3 бол F(x)=P(X=-1) + P(X=0)+ P(X=1)+ P(X=2)+P(X=3)= 0.1 +0.1 +0.3+0.2+0.3=1, учир нь x1=-1, x2=0, x3=1, x4=2 гэсэн дөрвөн утга (-∞;x) ба x5=3 интервалд ордог. https://pandia.ru/text/78/455/images/image006_89.gif" width="14 height=2" height="2"> x≤-1 дээр 0, -1 үед 0.1<х≤0, 0-д 0.2<х≤1, F(x)= 1-д 0.5<х≤2, 2 цагт 0.7<х≤3, x>3 үед 1 F(x) функцийг графикаар илэрхийлье (Зураг 3): https://pandia.ru/text/78/455/images/image014_24.jpg" өргөн "158 өндөр = 29" өндөр "29">≈1.2845. §
4. Хоёр гишүүнт тархалтын хууль дискрет санамсаргүй хэмжигдэхүүн, Пуассоны хууль. Тодорхойлолт: бином
салангид санамсаргүй хэмжигдэхүүний тархалтын хууль гэж нэрлэдэг X - n бие даасан давтан туршилтын үед А үйл явдал тохиолдох тоо, тус бүрт А үйл явдал p магадлалтай эсвэл q = 1-p магадлалаар тохиолдохгүй. Дараа нь P(X=m) - n туршилтаар А үйл явдлын яг m удаа тохиолдох магадлалыг Бернулли томъёогоор тооцоолно. Р(Х=m)=Сmnpmqn-m Хүлээлт, хэлбэлзэл, дундаж стандарт хэлбэлзэлХоёртын хуулийн дагуу тархсан X санамсаргүй хэмжигдэхүүнийг дараах томъёогоор олно. https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> Туршилт бүрт А үйл явдлын магадлал - "тав гаргах" нь ижил бөгөөд 1/6-тай тэнцүү байна. , өөрөөр хэлбэл P(A)=p=1/6, дараа нь P(A)=1-p=q=5/6, энд - "таваас унасан." Х санамсаргүй хэмжигдэхүүн нь дараах утгыг авч болно: 0;1;2;3. Бид Бернуллигийн томъёог ашиглан X-ийн боломжит утгуудын магадлалыг олно. Р(Х=0)=Р3(0)=С03р0q3=1 (1/6)0 (5/6)3=125/216; Р(Х=1)=Р3(1)=С13р1q2=3 (1/6)1 (5/6)2=75/216; Р(Х=2)=Р3(2)=С23р2q =3 (1/6)2 (5/6)1=15/216; Р(Х=3)=Р3(3)=С33р3q0=1 (1/6)3 (5/6)0=1/216. Тэр. X санамсаргүй хэмжигдэхүүний тархалтын хууль дараах хэлбэртэй байна. Хяналт: 125/216+75/216+15/216+1/216=1. X санамсаргүй хэмжигдэхүүний тоон шинж чанарыг олцгооё. M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, Даалгавар No4.Автомат машин эд ангиудыг тамгалдаг. Үйлдвэрлэсэн эд анги нь гэмтэлтэй байх магадлал 0.002 байна. Сонгогдсон 1000 хэсгээс дараах магадлалыг ол. a) 5 гэмтэлтэй; б) дор хаяж нэг нь гэмтэлтэй. Шийдэл:
n=1000 тоо нь их, гэмтэлтэй хэсэг үүсэх магадлал p=0.002 бага, авч үзэж буй үйл явдлууд (хэсэг нь гэмтэлтэй болсон) бие даасан байдаг тул Пуассоны томъёо дараах байдалтай байна. Рn(m)= д-
λ
λм λ=np=1000 0.002=2-ийг олъё. a) 5 гэмтэлтэй хэсэг байх магадлалыг ол (m=5): Р1000(5)= д-2
25
= 32 0,13534
= 0,0361 б) Дор хаяж нэг гэмтэлтэй хэсэг байх магадлалыг ол. А үйл явдал - "сонгосон хэсгүүдийн дор хаяж нэг нь гэмтэлтэй" нь үйл явдлын эсрэг байдаг - "сонгосон бүх хэсгүүд нь гэмтэлтэй биш. Тиймээс P(A) = 1-P(). Тиймээс шаардлагатай магадлал нь тэнцүү байна: P(A)=1-P1000(0)=1- д-2
20
= 1- e-2=1-0.13534≈0.865. Бие даасан ажилд зориулсан даалгавар.
1.1
1.2.
Тархсан санамсаргүй хэмжигдэхүүн X нь тархалтын хуулиар тодорхойлогддог. p4, тархалтын функц F(X)-ийг олоод түүний графикийг, мөн M(X), D(X), σ(X)-ийг зур. 1.3.
Хайрцагт 9 тэмдэглэгээ байгаа бөгөөд 2 нь бичихээ больсон. Санамсаргүй байдлаар 3 тэмдэглэгээ аваарай. Санамсаргүй хэмжигдэхүүн X нь авсан тэмдэглэгээнүүдийн дунд бичих тэмдэглэгээний тоо юм. Санамсаргүй хэмжигдэхүүний тархалтын хуулийг зур. 1.4.
Номын сангийн тавиур дээр санамсаргүй байдлаар байрлуулсан 6 сурах бичиг байдгаас 4 нь хавтастай. Номын санч 4 сурах бичгийг санамсаргүй байдлаар авдаг. Санамсаргүй хэмжигдэхүүн X нь авсан сурах бичгүүдийн дунд хавтасласан сурах бичгийн тоо юм. Санамсаргүй хэмжигдэхүүний тархалтын хуулийг зур. 1.5.
Тасалбар дээр хоёр даалгавар байна. Магадлал зөв шийдвэрэхний асуудал 0.9, хоёр дахь нь 0.7 байна. Санамсаргүй хувьсагч X нь тасалбар дахь зөв шийдэгдсэн асуудлын тоо юм. Тархалтын хуулийг гаргаж, энэ санамсаргүй хэмжигдэхүүний математик хүлээлт ба дисперсийг тооцож, мөн F(x) тархалтын функцийг олоод графикийг байгуул. 1.6.
Гурван буудагч бай руу буудаж байна. Нэг удаагийн сумаар бай онох магадлал нь эхний харваач 0.5, хоёр дахь нь 0.8, гурав дахь нь 0.7 байна. Х санамсаргүй хэмжигдэхүүн нь хэрэв буудагчид нэг удаад нэг удаа буудсан тохиолдолд бай онох тоо юм. M(X),D(X) тархалтын хуулийг ол. 1.7.
Сагсан бөмбөгийн тоглогч бөмбөгийг сагсанд шидэхэд шидэлт болгонд онох магадлал 0.8 байна. Оносон болгондоо 10 оноо авдаг бөгөөд алдсан тохиолдолд түүнд оноо өгөхгүй. Сагсан бөмбөгчний 3 цохилтоор авсан онооны тоо болох X санамсаргүй хэмжигдэхүүнийг хуваарилах хуулийг гарга. M(X),D(X), түүнчлэн 10-аас дээш оноо авах магадлалыг ол. 1.8.
Картууд дээр нийт 5 эгшиг, 3 гийгүүлэгч үсэг бичигдсэн байна. 3 картыг санамсаргүй байдлаар сонгох ба авсан картыг буцааж өгөх болгонд. Санамсаргүй хувьсагч X нь авсан эгшгийн тоо юм. Тархалтын хуулийг гаргаж M(X),D(X),σ(X)-ийг ол. 1.9.
Дунджаар гэрээний 60% Даатгалын компанидаатгалын тохиолдол гарсантай холбогдуулан даатгалын шимтгэл төлдөг. Санамсаргүй байдлаар сонгосон дөрвөн гэрээний дунд даатгалын төлбөрийг төлсөн гэрээний тоо болох X санамсаргүй хэмжигдэхүүнийг хуваарилах хуулийг гарга. Энэ хэмжигдэхүүний тоон шинж чанарыг ол. 1.10.
Радио станц нь дуудлагын дохиог (дөрвөөс илүүгүй) тодорхой интервалаар хоёр талын харилцаа холбоо тогтоох хүртэл илгээдэг. Дуудлагын дохионы хариуг хүлээн авах магадлал 0.3 байна. Санамсаргүй хувьсагч X нь илгээсэн дуудлагын тэмдгийн тоо юм. Тархалтын хуулийг гаргаж F(x)-ыг ол. 1.11.
3 түлхүүр байдаг бөгөөд тэдгээрийн зөвхөн нэг нь түгжээнд таардаг. Хэрэв оролдсон түлхүүр нь дараагийн оролдлогуудад оролцохгүй бол түгжээг онгойлгох оролдлогын тоо X санамсаргүй хэмжигдэхүүнийг хуваарилах хуулийг гарга. M(X),D(X)-ийг ол. 1.12.
Найдвартай байдлын үүднээс гурван төхөөрөмжийн бие даасан туршилтыг дараалан хийдэг. Бүр дараагийн төхөөрөмжөмнөх нь найдвартай болсон тохиолдолд л шалгана. Төхөөрөмж бүрийн туршилтыг давах магадлал 0.9 байна. Туршсан төхөөрөмжүүдийн санамсаргүй хэмжигдэхүүн X-тоо хуваарилах хуулийг гарга. 1.13
.Х дискрет санамсаргүй хэмжигдэхүүн нь x1=1, x2, x3, x1 гэсэн гурван боломжит утгатай байна.<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
Электрон төхөөрөмжийн блок нь 100 ижил элементийг агуулдаг. Т хугацааны туршид элемент бүрийн эвдрэл гарах магадлал 0.002 байна. Элементүүд бие даан ажилладаг. T хугацаанд хоёроос илүүгүй элемент ажиллахгүй байх магадлалыг ол. 1.15.
Сурах бичиг 50 мянган хувь хэвлэгджээ. Сурах бичиг буруу хавсаргасан байх магадлал 0.0002. Цуглуулга нь дараахь зүйлийг агуулсан байх магадлалыг ол. а) дөрвөн гэмтэлтэй ном, б) хоёроос бага гэмтэлтэй ном. 1
.16.
АТС-д минут тутамд ирж буй дуудлагын тоог Пуассоны хуулийн дагуу λ=1.5 параметртэй хуваарилдаг. Нэг минутын дараа дараахь зүйл ирэх магадлалыг ол. a) хоёр дуудлага; б) дор хаяж нэг дуудлага. 1.17.
Z=3X+Y бол M(Z),D(Z)-ийг ол. 1.18.
Хоёр бие даасан санамсаргүй хэмжигдэхүүний тархалтын хуулиудыг өгөв. Z=X+2Y бол M(Z),D(Z)-ийг ол. Хариултууд:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110"> 1.1.
p3=0.4; x≤-2 үед 0, -2 үед 0.3<х≤0, F(x)= 0-д 0.5<х≤2, 2 цагт 0.9<х≤5, x>5 үед 1 -1 үед 0.3<х≤0, 0-д 0.4<х≤1, F(x)= 1-д 0.6<х≤2, 2 цагт 0.7<х≤3, x>3 үед 1 M(X)=1; D(X)=2.6; σ(X) ≈1.612. https://pandia.ru/text/78/455/images/image025_24.gif" width="2 height=98" height="98"> 0-д x≤0, 0-д 0.03<х≤1, F(x)= 1-д 0.37<х≤2, x>2-д 1 M(X)=2; D(X)=0.62 M(X)=2.4; D(X)=0.48, P(X>10)=0.896 1.
8
.
M(X)=15/8; D(X)=45/64; σ(Х) ≈ M(X)=2.4; D(X)=0.96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(X)=2; D(X)=2/3 1.14.
1.22 e-0.2≈0.999 1.15.
a) 0.0189; b) 0.00049 1.16.
a) 0.0702; б) 0.77687 1.17.
3,8; 14,2 1.18.
11,2; 4. 2-р бүлэг. Тасралтгүй санамсаргүй хэмжигдэхүүн
Тодорхойлолт: Үргэлжилсэн
Тэд бүх боломжит утгууд нь тоон шугамын төгсгөлтэй эсвэл хязгааргүй хүрээг бүрэн дүүргэх хэмжигдэхүүнийг нэрлэдэг. Мэдээжийн хэрэг, тасралтгүй санамсаргүй хэмжигдэхүүний боломжит утгуудын тоо хязгааргүй байдаг. Тасралтгүй санамсаргүй хэмжигдэхүүнийг түгээлтийн функц ашиглан тодорхойлж болно. Тодорхойлолт:Ф түгээлтийн функц
тасралтгүй X санамсаргүй хэмжигдэхүүнийг F(x) функц гэж нэрлэдэг бөгөөд энэ нь утга тус бүрээр тодорхойлогддог xhttps://pandia.ru/text/78/455/images/image028_11.jpg" width="14" height="13"> Р Түгээлтийн функцийг заримдаа хуримтлагдсан тархалтын функц гэж нэрлэдэг. Түгээлтийн функцийн шинж чанарууд:
1)1≤ F(x) ≤1 2) Тасралтгүй санамсаргүй хэмжигдэхүүний хувьд тархалтын функц нь аль ч цэг дээр тасралтгүй бөгөөд тусдаа цэгүүдээс бусад газар бүрт дифференциалагдах боломжтой. 3) Санамсаргүй хэмжигдэхүүн X (a;b), [a;b], [a;b] интервалуудын аль нэгэнд орох магадлал нь F(x) функцийн утгуудын зөрүүтэй тэнцүү байна. a ба b цэгүүдэд, өөрөөр хэлбэл. R(a)<Х 4) Үргэлжилсэн санамсаргүй хэмжигдэхүүн X нэг тусдаа утгыг авах магадлал 0 байна. 5) F(-∞)=0, F(+∞)=1 Түгээлтийн функцийг ашиглан тасралтгүй санамсаргүй хэмжигдэхүүнийг тодорхойлох нь цорын ганц арга биш юм. Магадлалын тархалтын нягт (тархалтын нягт) гэсэн ойлголтыг танилцуулъя. Тодорхойлолт
:
Магадлалын тархалтын нягт
е
(
x
)
Үргэлжилсэн санамсаргүй хэмжигдэхүүн X нь түүний тархалтын функцийн дериватив, өөрөөр хэлбэл: Магадлалын нягтын функцийг заримдаа дифференциал тархалтын функц эсвэл дифференциал тархалтын хууль гэж нэрлэдэг. f(x) магадлалын нягтын тархалтын графикийг нэрлэнэ магадлалын тархалтын муруй
.
Магадлалын нягтын тархалтын шинж чанарууд:
1) f(x) ≥0, xhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" height="141">.gif" өргөн="14" өндөр ="62 src="> 0 үед x≤2, f(x)= c(x-2) 2-т<х≤6, x>6-д 0. Олно: a) c-ийн утгыг; б) тархалтын функц F(x) ба графикийг зурах; в) P(3≤x<5) Шийдэл:
+
∞ a) Нормчиллын нөхцлөөс c-ийн утгыг олно: ∫ f(x)dx=1. Тиймээс -∞ https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> -∞ 2 2 x хэрэв 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х - (4/2-4))= 1/8(x2/2-2x+2)=1/16(x-2)2; Gif" өргөн "14" өндөр "62"> x≤2 үед 0, F(x)= (x-2)2/16 дээр 2<х≤6, x>6-д 1. F(x) функцийн графикийг 3-р зурагт үзүүлэв https://pandia.ru/text/78/455/images/image034_23.gif" width="14" height="62 src="> x≤0 үед 0, 0-д F(x)= (3 арктан х)/π<х≤√3, x>√3-ийн хувьд 1. f(x) дифференциал тархалтын функцийг ол. Шийдэл:
f(x)= F’(x) тул https://pandia.ru/text/78/455/images/image011_36.jpg" өргөн "118" өндөр "24"> Тархсан санамсаргүй хэмжигдэхүүнүүдийн хувьд өмнө нь авч үзсэн математикийн хүлээлт ба дисперсийн бүх шинж чанарууд нь тасралтгүй хэмжигдэхүүнүүдэд мөн хүчинтэй байна. Даалгавар №3.Х санамсаргүй хэмжигдэхүүн өгөгдсөн дифференциал функц f(x): https://pandia.ru/text/78/455/images/image036_19.gif" height="38"> -∞ 2 X3/9 + x2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> +∞ D(X)= ∫ x2 f(x)dx-(M(x))2=∫ x2 x/3 dx+∫1/3x2 dx=(31/18)2=x4/12 + x3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. Бие даасан шийдлийн асуудлууд.
2.1.
Үргэлжилсэн санамсаргүй хэмжигдэхүүн X нь тархалтын функцээр тодорхойлогддог: x≤0 үед 0, F(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> x≤ π/6-д 0, F(x)= - π/6 үед cos 3x<х≤ π/3, x> π/3 хувьд 1. f(x) дифференциал тархалтын функцийг ол, мөн түүнчлэн Р(2π /9<Х< π /2). 2.3.
x≤2 үед 0, f(x)= c x 2 үед<х≤4, x>4-д 0. 2.4.
Тасралтгүй санамсаргүй хэмжигдэхүүн X нь тархалтын нягтралаар тодорхойлогддог. x≤0 үед 0, f(x)= 0-д c √x<х≤1, x>1-д 0. Олно: a) c тоо; b) M(X), D(X). 2.5.
https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" height="39"> x дээр, x үед 0. Олно: a) F(x) ба түүний графикийг байгуул; b) M(X),D(X), σ(X); в) дөрөв дэх магадлал бие даасан туршилтууд X утга нь (1;4) интервалд хамаарах утгыг яг 2 дахин авна. 2.6.
Үргэлжилсэн санамсаргүй хэмжигдэхүүн X-ийн магадлалын тархалтын нягтыг дараах байдлаар өгөв. f(x)= 2(x-2) үед x, x үед 0. Олно: a) F(x) ба түүний графикийг байгуул; b) M(X),D(X), σ (X); в) бие даасан гурван туршилтын үед X-ийн утга нь тухайн сегментийн утгаас яг 2 дахин их байх магадлал. 2.7.
f(x) функц нь дараах байдлаар өгөгдсөн. https://pandia.ru/text/78/455/images/image045_4.jpg" өргөн="43" өндөр="38 src=">.jpg" өргөн="16" өндөр="15">[-√ 3/2; √3/2]. 2.8.
f(x) функц нь дараах байдлаар өгөгдсөн. https://pandia.ru/text/78/455/images/image046_5.jpg" өргөн="45" өндөр="36 src="> .jpg" өргөн="16" өндөр="15">[- π /4 ; π /4]. Ол: a) ямар нэг санамсаргүй хэмжигдэхүүн X-ийн магадлалын нягтрал байх функц байх c тогтмолын утгыг; б) тархалтын функц F(x). 2.9.
(3;7) интервал дээр төвлөрсөн Х санамсаргүй хэмжигдэхүүнийг F(x)= тархалтын функцээр тодорхойлно. Ийм магадлалыг ол санамсаргүй хэмжигдэхүүн X нь дараах утгыг авна: a) 5-аас бага, б) 7-оос багагүй. 2.10.
Санамсаргүй хувьсагч X, интервал дээр төвлөрч (-1;4), F(x)= тархалтын функцээр өгөгдөнө. Ийм магадлалыг ол санамсаргүй хэмжигдэхүүн X нь дараах утгыг авна: a) 2-оос бага, б) 4-өөс багагүй. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" height="44 src="> .jpg" width="16" height="15">. Олно: a) c тоо; b) M(X); в) магадлал P(X> M(X)). 2.12.
Санамсаргүй хэмжигдэхүүнийг дифференциал тархалтын функцээр тодорхойлно. https://pandia.ru/text/78/455/images/image050_3.jpg" өргөн="60" өндөр="38 src=">.jpg" өргөн="16 өндөр=15" өндөр="15"> . Олно: a) M(X); б) магадлал P(X≤M(X)) 2.13.
Rem тархалтыг магадлалын нягтар тодорхойлно. https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" height="37"> x ≥0. f(x) нь үнэхээр магадлалын нягтын функц гэдгийг батал. 2.14.
Үргэлжилсэн санамсаргүй хэмжигдэхүүн X-ийн магадлалын тархалтын нягтыг дараах байдлаар өгөв. https://pandia.ru/text/78/455/images/image054_3.jpg" width="174" height="136 src=">(Зураг 4) 2.16.
Х санамсаргүй хэмжигдэхүүнийг хуулийн дагуу хуваарилдаг. зөв гурвалжин"(0;4) интервалд (Зураг 5). Бүх тооны шулуун дээрх f(x) магадлалын нягтын аналитик илэрхийллийг ол. Хариултууд
x≤0 үед 0, f(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> x≤ π/6-д 0, π/6 үед F(x)= 3sin 3x<х≤ π/3, x> π/3 хувьд 0. Үргэлжилсэн санамсаргүй хэмжигдэхүүн X байна нэгдсэн хуульХэрэв магадлалын тархалтын нягт нь f(x) энэ интервал дээр тогтмол бөгөөд түүний гадна талд 0-тэй тэнцүү байвал X-ийн бүх боломжит утгыг агуулсан тодорхой интервал (a;b) дээрх тархалт. x≤a-ийн хувьд 0, a-ийн хувьд f(x)=<х x≥b-ийн хувьд 0. f(x) функцийн графикийг Зураг дээр үзүүлэв. 1 F(x)= https://pandia.ru/text/78/455/images/image077_3.jpg" width="30" height="37">, D(X)=, σ(X)=. Даалгавар №1.Х санамсаргүй хэмжигдэхүүн сегмент дээр жигд тархсан байна. Олно: a) магадлалын тархалтын нягт f(x) ба графикийг зурах; б) тархалтын функц F(x) ба графикийг зурах; c) M(X),D(X), σ(X). Шийдэл:
Дээр авч үзсэн томьёог ашиглан a=3, b=7 гэсэн томъёогоор бид дараахь зүйлийг олно. https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" height="39"> 3≤х≤7, x>7-д 0 Түүний графикийг байгуулъя (Зураг 3): https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86 src="> x≤3 үед 0, F(x)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" height="119 src=">Зураг 4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" height="43">==https://pandia.ru/text/ 78/455/images/image092_10.gif" width="14" height="49 src="> x үед 0<0, x≥0-ийн хувьд f(x)= λе-λх. Экспоненциал хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүн X-ийн тархалтын функцийг дараах томъёогоор тодорхойлно. https://pandia.ru/text/78/455/images/image094_4.jpg" width="191" height="126 src=">fig..jpg" width="22" height="30"> , D(X)=, σ (Х)= Тиймээс математикийн хүлээлт ба экспоненциал тархалтын стандарт хазайлт нь хоорондоо тэнцүү байна. X-ийн (a;b) интервалд орох магадлалыг дараах томъёогоор тооцоолно. П(а<Х Даалгавар №2.Төхөөрөмжийн гэмтэлгүй ажиллах дундаж хугацаа 100 цаг байна. Төхөөрөмжийн гэмтэлгүй ажиллах хугацаа нь экспоненциал тархалтын хуультай гэж үзвэл дараахь зүйлийг ол. a) магадлалын тархалтын нягт; б) түгээлтийн функц; в) төхөөрөмжийн гэмтэлгүй ажиллах хугацаа 120 цагаас хэтрэх магадлал. Шийдэл:
Нөхцөлийн дагуу математикийн тархалт M(X)=https://pandia.ru/text/78/455/images/image098_10.gif" height="43 src="> 0 at x байна.<0, a) x≥0-ийн хувьд f(x)= 0.01e -0.01x. b) x үед F(x)= 0<0, x≥0 үед 1-e -0.01x. в) Хүссэн магадлалыг түгээлтийн функцээр олно. P(X>120)=1-F(120)=1-(1- e -1.2)= e -1.2≈0.3. §
3.Хэвийн хуваарилалтын хууль Тодорхойлолт:
Үргэлжилсэн санамсаргүй хэмжигдэхүүн X байна хэвийн тархалтын хууль (Гауссын хууль),
Хэрэв түүний тархалтын нягт нь дараах хэлбэртэй байвал: Энд m=M(X), σ2=D(X), σ>0. Хэвийн тархалтын муруйг нэрлэнэ хэвийн буюу Гауссын муруй
(Зураг 7) Х санамсаргүй хэмжигдэхүүний хэвийн хуулийн дагуу тархсан тархалтын функцийг Лаплас функцээр Ф (х) томъёогоор илэрхийлнэ. Лаплас функц хаана байна. Сэтгэгдэл:
Ф(х) функц нь сондгой (Ф(-х)=-Ф(х)) бөгөөд үүнээс гадна x>5 хувьд Ф(х) ≈1/2 гэж үзэж болно. F(x) тархалтын функцийн графикийг Зураг дээр үзүүлэв. 8 https://pandia.ru/text/78/455/images/image106_4.jpg" өргөн "218" өндөр "33"> Тийм магадлал үнэмлэхүй үнэ цэнэхазайлт бага байна эерэг тооδ-ийг дараах томъёогоор тооцоолно. Ялангуяа m=0-ийн хувьд дараахь тэгшитгэлийг хангана. "Гурван сигма дүрэм"
Хэрэв санамсаргүй хэмжигдэхүүн X нь m ба σ параметртэй хэвийн тархалтын хуультай бол түүний утга (a-3σ; a+3σ) интервалд байх нь бараг тодорхой болно, учир нь https://pandia.ru/text/78/455/images/image110_2.jpg" өргөн "157" өндөр "57 src=">a) б) томъёог ашиглая: https://pandia.ru/text/78/455/images/image112_2.jpg" өргөн "369" өндөр "38 src="> Ф(х) функцийн утгуудын хүснэгтээс Ф(1.5)=0.4332, Ф(1)=0.3413-ыг олно. Тэгэхээр, хүссэн магадлал: P(28 Бие даасан ажилд зориулсан даалгавар
3.1.
Х санамсаргүй хэмжигдэхүүн (-3;5) интервалд жигд тархсан байна. Олно: б) тархалтын функц F(x); в) тоон үзүүлэлтүүд; d) магадлал P(4<х<6). 3.2.
Х санамсаргүй хэмжигдэхүүн сегмент дээр жигд тархсан байна. Олно: a) тархалтын нягт f(x); б) тархалтын функц F(x); в) тоон үзүүлэлтүүд; г) магадлал P(3≤х≤6). 3.3.
Хурдны зам дээр автомат гэрлэн дохио байдаг бөгөөд ногоон гэрэл 2 минут, шар 3 секунд, улаан 30 секунд асдаг. Машин хурдны замаар санамсаргүй байдлаар явдаг. Машин гэрлэн дохионы хажуугаар зогсолтгүй өнгөрөх магадлалыг ол. 3.4.
Метроны галт тэрэг 2 минутын зайтай тогтмол явдаг. Зорчигч санамсаргүй байдлаар тавцан руу ордог. Зорчигч галт тэргийг 50 секундээс илүү хүлээх магадлал хэд вэ? Х санамсаргүй хэмжигдэхүүний математик хүлээлтийг олоорой - галт тэрэг хүлээх хугацаа. 3.5.
Түгээлтийн функцээр өгөгдсөн экспоненциал тархалтын дисперс ба стандарт хазайлтыг ол. X үед F(x)= 0<0, x≥0-д 1-8х. 3.6.
Үргэлжилсэн санамсаргүй хэмжигдэхүүн X нь магадлалын тархалтын нягтаар тодорхойлогддог. x үед f(x)= 0<0, x≥0 үед 0.7 e-0.7x. a) Харгалзан авч буй санамсаргүй хэмжигдэхүүний тархалтын хуулийг нэрлэнэ үү. б) Х санамсаргүй хэмжигдэхүүний F(X) тархалтын функц болон тоон шинж чанарыг ол. 3.7.
Х санамсаргүй хэмжигдэхүүнийг магадлалын тархалтын нягтаар тодорхойлсон экспоненциал хуулийн дагуу хуваарилна. x үед f(x)= 0<0, x≥0 үед 0.4 e-0.4 x. Туршилтын үр дүнд X (2.5;5) интервалаас утгыг авах магадлалыг ол. 3.8.
Тасралтгүй санамсаргүй хэмжигдэхүүн X нь тархалтын функцээр тодорхойлсон экспоненциал хуулийн дагуу тархдаг. X үед F(x)= 0<0, x≥0 үед 1-0.6x Туршилтын үр дүнд X сегментээс утгыг авах магадлалыг ол. 3.9.
Хэвийн тархалттай санамсаргүй хэмжигдэхүүний хүлээгдэж буй утга ба стандарт хазайлт нь 8 ба 2 байна. a) тархалтын нягт f(x); b) туршилтын үр дүнд X (10;14) интервалаас утгыг авах магадлал. 3.10.
Х санамсаргүй хэмжигдэхүүн нь математикийн хүлээлт 3.5, дисперс нь 0.04 байхаар хэвийн тархсан байна. Олно: a) тархалтын нягт f(x); б) туршилтын үр дүнд X сегментээс утгыг авах магадлал. 3.11.
Х санамсаргүй хэмжигдэхүүн нь M(X)=0, D(X)=1 гэсэн хэвийн тархалттай байна. |X|≤0.6 эсвэл |X|≥0.6 үйл явдлын аль нь илүү магадлалтай вэ? 3.12.
Х санамсаргүй хэмжигдэхүүн нь M(X)=0 ба D(X)=1-ээр хэвийн тархсан байна. Нэг тестийн үед аль интервалаас (-0.5;-0.1) эсвэл (1;2) утга авах боломжтой вэ? 3.13.
Хувьцааны одоогийн үнийг M(X)=10 дентэй хэвийн тархалтын хуулийг ашиглан загварчилж болно. нэгж ба σ (X)=0.3 ден. нэгж Олно: a) одоогийн хувьцааны үнэ 9.8 денээс байх магадлал. нэгж 10.4 хоног хүртэл нэгж; б) "гурван сигма дүрэм" -ийг ашиглан одоогийн хувьцааны үнэ байрлах хил хязгаарыг ол. 3.14.
Бодисыг системчилсэн алдаагүйгээр жинлэнэ. Санамсаргүй жинлэлтийн алдаа нь σ=5g дундаж квадрат харьцаатай хэвийн хуульд хамаарна. Дөрвөн бие даасан туршилтанд гурван жинлэлтийн алдаа 3r үнэмлэхүй утгад гарахгүй байх магадлалыг ол. 3.15.
Х санамсаргүй хэмжигдэхүүн нь M(X)=12.6-тай хэвийн тархалттай байна. Санамсаргүй хэмжигдэхүүн (11.4;13.8) интервалд орох магадлал 0.6826 байна. σ стандарт хазайлтыг ол. 3.16.
Х санамсаргүй хэмжигдэхүүн нь M(X)=12 ба D(X)=36 байхаар хэвийн тархсан байна.Тестийн үр дүнд X санамсаргүй хэмжигдэхүүн орох интервалыг 0.9973 магадлалаар ол. 3.17.
Автомат машинаар үйлдвэрлэсэн эд анги нь түүний хяналттай параметрийн X хазайлт нь нэрлэсэн утгаас 2 хэмжилтийн модулиас хэтэрсэн тохиолдолд гэмтэлтэй гэж тооцогддог. X санамсаргүй хэмжигдэхүүн нь M(X)=0, σ(X)=0.7 байхаар хэвийн тархсан гэж үздэг. Машин нь гэмтэлтэй эд ангиудын хэдэн хувийг үйлдвэрлэдэг вэ? 3.18.
Хэсгийн X параметр нь нэрлэсэн утгатай тэнцүү 2 математик хүлээлт, 0.014 стандарт хазайлтаар хэвийн тархсан байна. Х-ийн нэрлэсэн утгаас хазайх нь нэрлэсэн үнийн дүнгийн 1%-иас хэтрэхгүй байх магадлалыг ол. Хариултууд
https://pandia.ru/text/78/455/images/image116_9.gif" өргөн "14" өндөр "110 src="> b) x≤-3-ийн хувьд 0, F(x)= зүүн"> 3.10.
a)f(x)=, b) Р(3.1≤Х≤3.7) ≈0.8185. 3.11.
|x|≥0.6. 3.12.
(-0,5;-0,1). 3.13.
a) P(9.8≤Х≤10.4) ≈0.6562. 3.14.
0,111. 3.15.
σ=1.2. 3.16.
(-6;30). 3.17.
0,4%. X санамсаргүй хэмжигдэхүүний тархалтын хууль: Жишээ №2. Нэг буудагч нэг сумаар байг онох магадлал нь эхний харвагчийн хувьд 0.8, хоёр дахь нь 0.85 байна. Буудлагчид бай руу нэг удаа буудсан. Байгаа онохыг ганцаарчилсан буудлагын хувьд бие даасан үйл явдал гэж үзээд байн дээр яг нэг удаа онох А үйл явдлын магадлалыг ол. Санамсаргүй хувьсагч
Энэ нь янз бүрийн нөхцөл байдлаас шалтгаалан тодорхой утгыг авч чаддаг хувьсагч бөгөөд эргээд санамсаргүй хэмжигдэхүүн гэж нэрлэгддэг. салангид
, хэрэв түүний утгуудын багц нь хязгаарлагдмал эсвэл тоолох боломжтой бол. Дискрет санамсаргүй хэмжигдэхүүнүүдээс гадна тасралтгүй санамсаргүй хэмжигдэхүүнүүд бас байдаг. Санамсаргүй хэмжигдэхүүний тухай ойлголтыг илүү нарийвчлан авч үзье. Практикт тодорхой утгыг авч болох хэмжигдэхүүнүүд ихэвчлэн байдаг боловч авч үзэж буй туршлага, үзэгдэл, ажиглалтад тэдгээр нь тус бүр ямар үнэ цэнийг авахыг найдвартай урьдчилан таамаглах боломжгүй юм. Жишээлбэл, дараагийн өдөр Москвад төрөх хөвгүүдийн тоо өөр байж болно. Энэ нь тэгтэй тэнцүү байж болно (нэг ч хүү төрөхгүй: бүх охид төрөх эсвэл шинэ төрсөн хүүхэд огт төрөхгүй), нэг, хоёр гэх мэт төгсгөлтэй тоо гарах хүртэл байж болно. n. Ийм утгууд нь: талбай дээрх чихрийн нишингийн үндэс, их бууны нисэх зай, багц дахь гэмтэлтэй хэсгүүдийн тоо гэх мэт. Бид ийм хэмжигдэхүүнийг санамсаргүй гэж нэрлэх болно. Эдгээр нь туршлага эсвэл ажиглалтын бүх боломжит үр дүнг тоон үүднээс тодорхойлдог. Дискрет санамсаргүй хэмжигдэхүүнүүдийн жишээ
Хязгаарлагдмал тооны утгууд нь хүн ам суурьшсан газарт өдрийн цагаар төрсөн хүүхдийн тоо, автобусны зорчигчдын тоо, Москвагийн метрогоор өдөрт тээвэрлэсэн зорчигчдын тоо гэх мэт байж болно. Дискрет санамсаргүй хэмжигдэхүүний утгуудын тоо нь хязгааргүй, гэхдээ тоолж болох олонлог байж болно. Гэхдээ ямар ч тохиолдолд тэдгээрийг ямар нэг дарааллаар дугаарлаж болно, эсвэл илүү нарийвчлалтай, санамсаргүй хэмжигдэхүүний утга ба 1, 2, 3, ... натурал тоонуудын хооронд нэг нэгээр нь захидал харилцааг тогтоож болно. , n. Анхаар: магадлалын онолын шинэ, маш чухал ойлголт - хуваарилалтын хууль
. Болъё Xхүлээн зөвшөөрч чадна nүнэт зүйлс: . Бид тэдгээр нь бүгд өөр өөр (өөрөөр бол ижил хүмүүсийг нэгтгэх ёстой) бөгөөд өсөх дарааллаар байрлуулсан гэж бид таамаглах болно. Дискрет санамсаргүй хэмжигдэхүүнийг бүрэн тодорхойлох зөвхөн түүний бүх утгыг төдийгүй магадлалыг зааж өгөх ёстой
Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль
аливаа дүрэм (функц, хүснэгт) дуудагдана х(x), энэ нь санамсаргүй хэмжигдэхүүнтэй холбоотой бүх төрлийн үйл явдлын магадлалыг олох боломжийг олгодог (жишээлбэл, энэ нь ямар нэг утгын жишээ байх эсвэл зарим интервалд орох магадлал). Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийг дараах хүснэгтийн хэлбэрээр тогтоох нь хамгийн энгийн бөгөөд тохиромжтой. Энэ хүснэгтийг нэрлэдэг дискрет санамсаргүй хэмжигдэхүүний тархалтын ойролцоо. Тархалтын цувралын дээд мөрөнд салангид санамсаргүй хэмжигдэхүүний (x) бүх боломжит утгуудыг өсөх дарааллаар жагсаасан ба доод мөрөнд эдгээр утгуудын магадлалыг ( х). Үйл явдал Жишээ 1.Оюутны бүлэгт сугалаа зохион байгууллаа. 1000 рублийн үнэтэй хоёр зүйлийг худалдаж авах боломжтой. нэг нь 3000 рублийн үнэтэй. Нэг тасалбарыг 100 рублиэр худалдаж авсан оюутны цэвэр хожлын хэмжээг хуваарилах хуулийг гарга. Нийт 50 тасалбар зарагдсан. Шийдэл. Бидний сонирхож буй санамсаргүй хэмжигдэхүүн бол Xгурван утгыг авч болно: - 100 урэх. (хэрэв оюутан ялаагүй, гэхдээ тасалбарын төлбөрт төлсөн 100 рубль алдвал), 900 рубль. ба 2900 рубль. (бодит ялалт нь 100 рубль - тасалбарын үнээр буурсан). Эхний үр дүн 50-аас 47 удаа, хоёр дахь нь 2, гурав дахь нь нэг байна. Тиймээс тэдний магадлал нь: П(X=-100)=47/50=0,94
,
П(X=900)=2/50=0,04
,
П(X=2900)=1/50=0,02
. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль Xшиг харагдаж байна Тархалтын цувааг зөвхөн салангид санамсаргүй хэмжигдэхүүнд зориулж байгуулж болно (дискрет бус санамсаргүй хэмжигдэхүүний хувьд үүнийг бүтээх боломжгүй, хэрэв ийм санамсаргүй хэмжигдэхүүний боломжит утгуудын багцыг тоолох боломжгүй бол тэдгээрийг дээд хэсэгт жагсаах боломжгүй бол) хүснэгтийн эгнээ). Бүх санамсаргүй хэмжигдэхүүнүүдэд (дискрет ба салангид бус) тохиромжтой тархалтын хуулийн хамгийн ерөнхий хэлбэр нь тархалтын функц юм. Дискрет санамсаргүй хэмжигдэхүүний тархалтын функцэсвэл интеграл функцфункц гэж нэрлэдэг Аливаа салангид санамсаргүй хэмжигдэхүүний тархалтын функц нь тасалдалтай алхам функц бөгөөд түүний үсрэлт нь санамсаргүй хэмжигдэхүүний боломжит утгуудтай харгалзах цэгүүдэд тохиолддог бөгөөд эдгээр утгуудын магадлалтай тэнцүү байна. Жишээ 2.Дискрет санамсаргүй хэмжигдэхүүн X- үхэл шидэх үед авсан онооны тоо. Түүний тархалтын функцийг тооцоол. Шийдэл. Дискрет санамсаргүй хэмжигдэхүүний тархалтын цуваа Xхэлбэртэй байна: Түгээлтийн функц Ф(x) нь 1/6 хэмжээтэй тэнцүү 6 үсрэлттэй (доорх зурагт). Жишээ 3.Цүнхэнд 6 цагаан, 4 хар бөмбөг байна. Урдаас 3 бөмбөг сугалж авдаг. Сугалсан бөмбөгнүүдийн дундах цагаан бөмбөгний тоо нь салангид санамсаргүй хэмжигдэхүүн юм X. Түүнд тохирсон хуваарилалтын хуулийг гарга. X 0, 1, 2, 3 утгыг авч болно. Харгалзах магадлалыг ашиглан хамгийн хялбар тооцоолж болно. магадлалыг үржүүлэх дүрэм. Бид дискрет санамсаргүй хэмжигдэхүүний тархалтын дараах хуулийг олж авна. Жишээ 4.Дискрет санамсаргүй хэмжигдэхүүнийг хуваарилах хуулийг гаргана уу - нэг цохилтоор онох магадлал 0.1 бол байг дөрвөн цохилтоор онох тоо. Шийдэл. Дискрет санамсаргүй хэмжигдэхүүн X 1, 2, 3, 4, 5 гэсэн таван өөр утгыг авч болно. Бид харгалзах магадлалыг ашиглан олдог. Бернуллигийн томъёо
n = 4
, х = 1,1
, q = 1 - х = 0,9
, м = 0, 1, 2, 3, 4
бид авдаг Улмаар дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль Xшиг харагдаж байна Хэрэв дискрет санамсаргүй хэмжигдэхүүний утгын магадлалыг Бернулли томъёогоор тодорхойлж чадвал санамсаргүй хэмжигдэхүүн нь дараах байдалтай байна. бином тархалт . Хэрэв туршилтын тоо хангалттай их байвал эдгээр туршилтуудад сонирхолтой тохиолдол гарах магадлал өндөр байна мудаа, хуулийг дагаж мөрддөг Пуассоны тархалт . Дискрет санамсаргүй хэмжигдэхүүний тархалтын функцийг тооцоолох Ф(X), хилийн утгаас бага буюу тэнцүү байгаа бүх утгуудын магадлалыг нэмэх шаардлагатай. X. Жишээ 5.Жилийн туршид салсан гэрлэлтийн тоо нь гэрлэлтийн үргэлжлэх хугацаанаас хамаарч байгааг хүснэгтэд үзүүлэв. Дараагийн салсан гэрлэлт 5 жилээс бага буюу тэнцүү жил үргэлжилсэн байх магадлалыг ол. Шийдэл. Магадлалыг тооцож, харгалзах салсан гэрлэлтийн тоог нийт 6010-д хуваана. Дараагийн салсан гэрлэлт 5 жил үргэлжилсэн байх магадлал 0.056 байна. Дараагийн салсан гэрлэлтийн үргэлжлэх хугацаа 5 жилээс бага буюу тэнцүү байх магадлал 0.186 байна. Бид үүнийг үнэ цэнийг нэмснээр олж авсан Ф(x) 4 жилийн хугацаатай гэрлэлтийн хувьд, 5 жилийн хугацаатай гэрлэлтийн магадлал. Дискрет санамсаргүй хэмжигдэхүүний бүх утгууд ихэвчлэн мэдэгддэггүй, гэхдээ цувралын зарим утга эсвэл магадлалыг мэддэг, түүнчлэн санамсаргүй хэмжигдэхүүний математикийн хүлээлт ба (эсвэл) дисперс, үүнд тусдаа хичээл зориулагдсан болно. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийг гаргахад тус болох энэ хичээлээс зарим томъёог энд толилуулж, ийм асуудлыг шийдвэрлэх жишээг харцгаая. Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлт нь түүний бүх боломжит утгуудын үржвэрийн нийлбэр ба эдгээр утгуудын магадлал юм. Тодорхойлолтоор салангид санамсаргүй хэмжигдэхүүний дисперсийн томъёо нь: Ихэнхдээ дараахь тархалтын томъёо нь тооцоололд илүү тохиромжтой байдаг. Хаана Жишээ 6.Дискрет санамсаргүй хэмжигдэхүүн Xзөвхөн хоёр утгыг авч болно. Энэ нь магадлал бүхий бага утгыг авдаг х= 0.6. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийг ол X, хэрэв түүний математик хүлээлт ба дисперс нь мэдэгдэж байгаа бол . Шийдэл. Санамсаргүй хэмжигдэхүүн илүү их утгыг авах магадлал x2
, нь 1 − 0.6 = 4-тэй тэнцүү байна. Математикийн хүлээлтийн томъёог (1) ашиглан бид үл мэдэгдэх нь бидний салангид санамсаргүй хэмжигдэхүүний утгууд болох тэгшитгэлийг үүсгэдэг. Тархалтын томъёог (2) ашиглан бид үл мэдэгдэх нь салангид санамсаргүй хэмжигдэхүүний утгууд болох өөр нэг тэгшитгэлийг үүсгэдэг. Олж авсан хоёр тэгшитгэлийн систем орлуулах аргаар шийдвэрлэх. Эхний тэгшитгэлээс бид олж авдаг Энэ илэрхийлэлийг хоёр дахь тэгшитгэлд орлуулснаар бид энгийн хувиргалтуудыг олж авна квадрат тэгшитгэл 7/5 ба −1 гэсэн хоёр үндэстэй. Эхний үндэс нь асуудлын нөхцөлийг хангадаггүй тул x2
< x 1
. Тиймээс салангид санамсаргүй хэмжигдэхүүн авч болох утгууд Xбидний жишээний нөхцлийн дагуу тэнцүү байна x1
= −1
Тэгээд x2
= 2
. Дискрет санамсаргүй хэмжигдэхүүний тархалтын цуваа өгөгдсөн. Алга болсон магадлалыг олоод тархалтын функцийг зур. Энэ хэмжигдэхүүний математик хүлээлт ба дисперсийг тооцоол. Санамсаргүй хэмжигдэхүүн X нь зөвхөн дөрвөн утгыг авдаг: -4, -3, 1, 2. Энэ нь эдгээр утгууд тус бүрийг тодорхой магадлалтайгаар авдаг. Бүх магадлалын нийлбэр нь 1-тэй тэнцүү байх ёстой тул алдагдсан магадлал нь дараахтай тэнцүү байна. 0,3 + ? + 0,1 + 0,4 = 1, Х санамсаргүй хэмжигдэхүүний тархалтын функцийг зохиоё. Тархалтын функц нь мэдэгдэж байна, тэгвэл: Тиймээс, Функцийн графикийг зурцгаая Ф(x)
. Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлт нь санамсаргүй хэмжигдэхүүний утга ба харгалзах магадлалын бүтээгдэхүүний нийлбэртэй тэнцүү байна, өөрөөр хэлбэл. Дискрет санамсаргүй хэмжигдэхүүний дисперсийг бид дараах томъёогоор олно. Энд: - тооны факториал Үйл явдал гэдэг нь туршлагын үр дүнд тохиолдож болох эсвэл болохгүй аливаа баримт юм. Үйл явдлуудыг нэгтгэх АТэгээд IN- энэ үйл явдал ХАМТхарагдах байдал эсвэл үйл явдлаас бүрддэг А, эсвэл үйл явдал IN, эсвэл хоёр үйл явдлыг нэгэн зэрэг. Зориулалт: Хөндлөн гарах үйл явдлууд АТэгээд IN- энэ үйл явдал ХАМТ, энэ нь хоёр үйл явдлын нэгэн зэрэг явагдахаас бүрддэг. Зориулалт: Үйл явдлын магадлал Атуршилтын тооны харьцаа юм Үйл явдлын магадлал Хэрэв А ба В үйл явдлууд бие даасан байвал (нэг нь тохиолдсон нь нөгөө нь тохиолдоход нөлөөлөхгүй) бол үйл явдлын магадлал дараах байдалтай тэнцүү байна. Үйл явдлын магадлал Үйл явдлын магадлал А, Үйл явдлын магадлал IN, Хэрэв А ба В үйл явдлууд нийцэхгүй бол (нэг зэрэг тохиолдох боломжгүй) тохиолдлын магадлал дараах байдалтай тэнцүү байна. Үйл явдал болъё Аүйл явдлын аль нэгтэй зэрэгцэн тохиолдож болно Бие даасан n тест байх болтугай. Үйл явдал тохиолдох (амжилт) магадлал Атус бүр нь тогтмол бөгөөд тэнцүү байна х, бүтэлгүйтлийн магадлал (жишээ нь болоогүй үйл явдал А) q
=
1 - х. Дараа нь тохиолдох магадлал камжилт nТуршилтыг Бернуллигийн томъёог ашиглан олж болно. Хамгийн их магадлалтай амжилтын тоо салангид тасралтгүй (жишээ нь, 5 хүүхэдтэй айлын охидын тоо) (жишээлбэл, данх зөв ажиллах цаг) Дискрет хэмжигдэхүүнийг түгээлтийн цуваагаар өгье. , , …, - санамсаргүй хэмжигдэхүүний утгууд X; , , …, харгалзах магадлалын утгууд юм. Санамсаргүй хэмжигдэхүүний тархалтын функц Xгэсэн магадлалтай тэнцүү бүх тооны шулуун дээр тодорхойлогдсон функц юм Xбага байх болно X: Үйл явдал. Санамсаргүй үйл явдал дээрх үйлдлүүд. Үйл явдлын магадлалын тухай ойлголт. Магадлалыг нэмэх, үржүүлэх дүрэм. Нөхцөлт магадлал. Нийт магадлалын томъёо. Бэйсийн томъёо. Бернулли схем. Санамсаргүй хэмжигдэхүүн, түүний тархалтын функц ба тархалтын цуваа. Түгээлтийн функцийн үндсэн шинж чанарууд. Хүлээгдэж буй үнэ цэнэ. Математикийн хүлээлтийн шинж чанарууд. Тархалт. Тархалтын төрлүүд: жигд, экспоненциал, хэвийн, бином ба Пуассоны тархалт. Мойвр-Лапласын локал ба интеграл теоремууд. Хоёр санамсаргүй хэмжигдэхүүний системийн хууль ба тархалтын функц. Хоёр санамсаргүй хэмжигдэхүүний системийн тархалтын нягт. Тархалтын нөхцөлт хууль, нөхцөлт математик хүлээлт. Хамааралтай ба бие даасан санамсаргүй хэмжигдэхүүнүүд. Корреляцийн коэффициент. Дээж. Дээж боловсруулах. Полигон ба давтамжийн гистограм. Эмпирик тархалтын функц. Тархалтын параметрүүдийг тооцоолох тухай ойлголт. Үнэлгээнд тавигдах шаардлага. Итгэлийн интервал. Математикийн хүлээлт ба стандарт хазайлтыг тооцоолох интервалуудыг байгуулах. Статистикийн таамаглал. Зөвшөөрлийн шалгуур. Магадлалын онолын хэрэглээнд туршилтын тоон шинж чанар нь хамгийн чухал ач холбогдолтой юм. Туршилтын үр дүнд тухайн тохиолдлоос хамааран өөр өөр утгыг авах боломжтой тоон хэмжигдэхүүнийг нэрлэдэг. санамсаргүй хувьсагч. Санамсаргүй хэмжигдэхүүнүүдийн жишээ: 1. Арав шидэхэд тэгш тооны оноо гарч ирэх тоо. 2. Цуврал харваж буй харваачийн бай оносон тоо. 3. Тэсэрч буй бүрхүүлийн хэлтэрхийний тоо. Өгөгдсөн жишээ бүрт санамсаргүй хэмжигдэхүүн нь зөвхөн тусгаарлагдсан утгуудыг, өөрөөр хэлбэл байгалийн цуврал тоонуудыг ашиглан дугаарлаж болох утгуудыг авч болно. Ийм санамсаргүй хэмжигдэхүүн гэж нэрлэгддэг, боломжит утгууд нь тусдаа тусгаарлагдсан тоонууд бөгөөд энэ хувьсагч тодорхой магадлалаар авдаг. салангид. Дискрет санамсаргүй хэмжигдэхүүний боломжит утгуудын тоо нь төгсгөлтэй эсвэл хязгааргүй (тоолж болох) байж болно.Хуваарилалтын хууль Дискрет санамсаргүй хэмжигдэхүүн нь түүний боломжит утгууд ба тэдгээрийн харгалзах магадлалын жагсаалт юм. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийг хүснэгт хэлбэрээр (магадлалын тархалтын цуваа), аналитик болон графикаар (магадлалын тархалтын полигон) зааж өгч болно. Туршилт хийхдээ судалж буй утгыг "дунджаар" үнэлэх шаардлагатай болдог. Санамсаргүй хэмжигдэхүүний дундаж утгын үүргийг тоон шинж чанар гэж нэрлэдэгматематикийн хүлээлт, томъёогоор тодорхойлогддог x 1 Хаана 2
,.. , x n, x X– санамсаргүй хэмжигдэхүүний утгууд , А 1 ,х 2 ,
... , х nх х 1
+
х 2
+…+
х n =
1). - эдгээр утгын магадлал (үүнийг анхаарна уу I-д цохилт нь гурван оноо, II-д - хоёр оноо, III-д - нэг оноо өгдөг. Нэг шидэгчийн нэг цохилтонд авсан онооны тоо нь хэлбэрийн тархалтын хуультай Буудлагын ур чадварыг харьцуулахын тулд авсан онооны дундаж утгыг харьцуулах нь хангалттай юм. математикийн хүлээлт М(X) Мөн М(Ю):
М(X)
=
1
0,4
+ 2
0,2
+ 3
0,4
= 2,0, М(Ю)
=
1
0,2
+ 2
0,5
+ 3
0,3
= 2,1. Хоёр дахь мэргэн бууч дунджаар арай илүү оноо өгдөг, i.e. дахин дахин галлавал илүү сайн үр дүн өгнө. Математикийн хүлээлтийн шинж чанаруудыг тэмдэглэе. 1. Тогтмол утгын математик хүлээлт нь тогтмолтой тэнцүү байна: М(C)
= C. 2. Санамсаргүй хэмжигдэхүүний нийлбэрийн математик хүлээлт нь нэр томъёоны математик хүлээлтийн нийлбэртэй тэнцүү байна. М =(X 1 +
X 2 +…+
X n)=
М(X 1)+
М(X 2)+…+
М(X n). 3. Харилцан хамааралгүй санамсаргүй хэмжигдэхүүний үржвэрийн математик хүлээлт нь хүчин зүйлсийн математик хүлээлтийн үржвэртэй тэнцүү байна. М(X 1 X 2 …
X n)
=
М(X 1)М(X 2)…
М(X n). 4. Дуран тархалтын математик үгүйсгэл нь туршилтын тоо ба нэг туршилтанд тохиолдох үйл явдлын магадлалын үржвэртэй тэнцүү байна (даалгавар 4.6). М(X)
= pr. Санамсаргүй хэмжигдэхүүн нь "дунджаар" математикийн хүлээлтээс хэрхэн хазайж байгааг үнэлэхийн тулд, өөрөөр хэлбэл. Магадлалын онолд санамсаргүй хэмжигдэхүүний утгын тархалтыг тодорхойлохын тулд дисперсийн тухай ойлголтыг ашигладаг. Зөрчилсанамсаргүй хувьсагч Xквадрат хазайлтын математик хүлээлт гэж нэрлэдэг: Д(X)
=
М[(X
-
М(X)) 2 ]. Тархалт нь санамсаргүй хэмжигдэхүүний тархалтын тоон шинж чанар юм. Тодорхойлолтоос харахад санамсаргүй хэмжигдэхүүний тархалт бага байх тусам түүний боломжит утгууд нь математикийн хүлээлтийн эргэн тойронд илүү ойрхон байрладаг, өөрөөр хэлбэл санамсаргүй хэмжигдэхүүний утга нь түүний математик хүлээлтээр тодорхойлогддог нь тодорхой байна. . Тодорхойлолтоос харахад зөрүүг томъёогоор тооцоолж болно Өөр томъёог ашиглан зөрүүг тооцоолох нь тохиромжтой: Д(X)
=
М(X 2)
- (М(X)) 2 .
Тархалт нь дараахь шинж чанартай байдаг. 1. Тогтмол хэмжигдэхүүний дисперс нь тэг байна: Д(C)
=
0.
2. Тогтмол коэффициентийг квадрат болгож дисперсийн тэмдгээс гаргаж болно. Д(CX)
=
C 2 Д(X). 3. Бие даасан санамсаргүй хэмжигдэхүүний нийлбэрийн дисперс нь нэр томъёоны дисперсийн нийлбэртэй тэнцүү байна. Д(X 1 +
X 2 +
X 3 +…+
X n)=
Д(X 1)+
Д(X 2)+…+
Д(X n) 4. Хоёр гишүүний тархалтын дисперс нь туршилтын тоо болон нэг туршилтын үед тохиолдох болон тохиолдохгүй байх магадлалын үржвэртэй тэнцүү байна. Д(X)
= npq. Магадлалын онолд санамсаргүй хэмжигдэхүүний дисперсийн квадрат язгууртай тэнцүү тоон шинж чанарыг ихэвчлэн ашигладаг. Энэ тоон шинж чанарыг дундаж квадрат хазайлт гэж нэрлэдэг бөгөөд тэмдэгээр тэмдэглэнэ Энэ нь санамсаргүй хэмжигдэхүүний дундаж утгаас хазайх ойролцоо хэмжээг тодорхойлдог бөгөөд санамсаргүй хэмжигдэхүүнтэй ижил хэмжээтэй байна. 4.1.
Буудагч бай руу гурван удаа бууддаг. Буудсан болгонд бай онох магадлал 0.3 байна. Үзсэн тоогоор түгээлтийн цувралыг байгуул. Шийдэл. Үзсэн тоо нь салангид санамсаргүй хэмжигдэхүүн юм X. Утга бүр x n
санамсаргүй хувьсагч Xтодорхой магадлалтай тохирч байна П n . Энэ тохиолдолд дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийг тодорхойлж болно түгээлтийн ойролцоо. Энэ асуудалд X 0, 1, 2, 3 утгыг авна. Бернуллигийн томъёогоор Санамсаргүй хэмжигдэхүүний боломжит утгуудын магадлалыг олцгооё. Р 3 (0)
= (0,7) 3 =
0,343, Р 3 (1)
= Р 3 (2)
= Р 3 (3)
= (0,3) 3 =
0,027. Санамсаргүй хэмжигдэхүүний утгыг цэгцлэх замаар Xөсөх дарааллаар бид түгээлтийн цувралыг олж авна. X n Хэмжээ гэдгийг анхаарна уу санамсаргүй хэмжигдэхүүн байх магадлалыг хэлнэ Xболомжит утгуудаас дор хаяж нэг утгыг авах бөгөөд энэ үйл явдал найдвартай учраас 4.2
.Унганд 1-ээс 4 хүртэлх тооны дөрвөн бөмбөг байна. Хоёр бөмбөгийг гаргана. Санамсаргүй утга X- бөмбөгний тоонуудын нийлбэр. Санамсаргүй хэмжигдэхүүний тархалтын цуваа байгуул X. Шийдэл.Санамсаргүй хувьсагчийн утгууд X 3, 4, 5, 6, 7. Харгалзах магадлалыг олъё. Санамсаргүй хувьсагчийн утга 3 XСонгосон бөмбөгнүүдийн аль нэг нь 1, нөгөө нь 2-той тохиолдолд л зөвшөөрөгдөх боломжтой. Туршилтын боломжит үр дүнгийн тоо нь дөрөв (боломжтой хос бөмбөгний тоо) хоёрын хослолын тоотой тэнцүү байна. Сонгодог магадлалын томъёог ашиглан бид олж авна Үүний нэгэн адил, Р(X= 4) =Р(X= 6) =Р(X= 7) = 1/6. 5 нийлбэр нь 1 + 4 ба 2 + 3 гэсэн хоёр тохиолдолд гарч ирж болно Xхэлбэртэй байна: Түгээлтийн функцийг ол Ф(x) санамсаргүй хэмжигдэхүүн Xмөн үүнийг төлөвлө. -д зориулж тооцоол Xтүүний математик хүлээлт ба дисперс. Шийдэл. Санамсаргүй хэмжигдэхүүний тархалтын хуулийг тархалтын функцээр тодорхойлж болно Ф(x)
= П(X
x).
Түгээлтийн функц Ф(x) нь бүх тооны шулуун дээр тодорхойлогдсон буурдаггүй, зүүн тасралтгүй функц юм, while Ф
(-
)=
0,Ф
(+
)=
1. Дискрет санамсаргүй хэмжигдэхүүний хувьд энэ функцийг томъёогоор илэрхийлнэ Тиймээс энэ тохиолдолд Түгээлтийн функцийн график Ф(x) нь шаталсан шугам юм (Зураг 12) Ф(x) Хүлээгдэж буй үнэ цэнэМ(X) нь утгуудын жигнэсэн арифметик дундаж юм X 1 , X 2 ,……X nсанамсаргүй хувьсагч Xмасштабтай ρ
1,
ρ
2, ……
, ρ
n
ба санамсаргүй хэмжигдэхүүний дундаж утга гэнэ X. Томъёоны дагуу М(X)= x 1
ρ
1 + x 2
ρ
2 +……+ x n
ρ
n М(X) = 3·0.14+5·0.2+7·0.49+11·0.17 = 6.72. Тархалтсанамсаргүй хэмжигдэхүүний утгуудын тархалтын түвшинг дундаж утгаас нь тодорхойлж, тэмдэглэнэ. Д(X): Д(X)=М[(ХМ(X)) 2 ]= М(X 2)
–[М(X)] 2 . Дискрет санамсаргүй хэмжигдэхүүний хувьд дисперс нь хэлбэртэй байна эсвэл томъёогоор тооцоолж болно Асуудлын тоон өгөгдлийг томъёонд орлуулснаар бид дараахь зүйлийг авна. М(X 2)
=
3 2
∙ 0,14+5 2
∙ 0,2+7 2
∙ 0,49+11 2
∙ 0,17 = 50,84 Д(X)
= 50,84-6,72 2
= 5,6816. 4.4.
Хоёр шоо нэгэн зэрэг хоёр удаа шидэгддэг. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хоёр гишүүний хуулийг бич X- хоёр шоо дээрх тэгш тооны онооны тохиолдлын тоо. Шийдэл. Санамсаргүй үйл явдлыг танилцуулъя А= (нэг шидэлттэй хоёр шоо нийт тэгш тооны оноотой болсон). Магадлалын сонгодог тодорхойлолтыг ашиглан бид олдог Р(А)=
Хаана n
- шалгалтын боломжит үр дүнгийн тоог дүрмээр олно үржүүлэх: n
= 6∙6 =36, м
-
үйл явдлыг дэмжсэн хүмүүсийн тоо Аүр дүн - тэнцүү м= 3∙6=18. Тиймээс нэг туршилтанд амжилтанд хүрэх магадлал өндөр байна ρ
= П(А)=
1/2.
Асуудлыг Бернулли туршилтын схемийг ашиглан шийддэг. Энд нэг сорилт бол хоёр шоо нэг удаа өнхрүүлэх явдал юм. Ийм туршилтын тоо n
= 2. Санамсаргүй хувьсагч X 0, 1, 2 утгыг магадлалын хамт авна Р 2 (0)
= Санамсаргүй хэмжигдэхүүний хүссэн бином тархалт Xтүгээлтийн цуврал хэлбэрээр төлөөлж болно: X n ρ
n 4.5
. Зургаан хэсгээс бүрдсэн багцад дөрвөн стандарт хэсэг байдаг. Гурван хэсгийг санамсаргүй байдлаар сонгосон. Дискрет санамсаргүй хэмжигдэхүүний магадлалын тархалтыг байгуул X- Сонгогдсон хэсгүүдийн стандарт хэсгүүдийн тоог гаргаж, математикийн хүлээлтийг олоорой. Шийдэл.Санамсаргүй хувьсагчийн утгууд X 0,1,2,3 тоонууд. Энэ нь ойлгомжтой Р(XСтандарт бус хоёр л хэсэг байгаа тул =0)=0. Р(X=1) = Р(X= 2) = Р(X=3) = Санамсаргүй хэмжигдэхүүний тархалтын хууль XҮүнийг түгээлтийн цуврал хэлбэрээр толилуулъя: X n ρ
n Хүлээгдэж буй үнэ цэнэ М(X)=1
∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2. 4.6
. Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлт гэдгийг батал X- үйл явдлын тохиолдлын тоо АВ nбие даасан туршилтууд, тэдгээр нь тус бүрт үйл явдлын магадлал тэнцүү байна ρ
– нэг туршилтанд тохиолдох үйл явдлын магадлалын туршилтын тоог үржүүлсэн үржвэртэй тэнцүү, өөрөөр хэлбэл бином тархалтын математик хүлээлтийг нотлох. М(X)
=n .
ρ
, ба тархалт Д(X)
=n.p.
. Шийдэл.Санамсаргүй утга X 0, 1, 2... утгыг авч болно, n. Магадлал Р(X= k) Бернуллигийн томъёог ашиглан олно: Р(X=k)= Р n(k)= Санамсаргүй хэмжигдэхүүний тархалтын цуваа Xхэлбэртэй байна: X n ρ
n q n Хаана q=
1-
ρ
. Математикийн хүлээлтийн хувьд бид дараах илэрхийлэлтэй байна. М(X)= Нэг тестийн хувьд, өөрөөр хэлбэл хамт n = 1 санамсаргүй хэмжигдэхүүн X 1 - үйл явдлын тохиолдлын тоо А- түгээлтийн цуврал нь дараах хэлбэртэй байна. X n ρ
n М(X 1)=
0∙q +
1
∙ х
=
х Д(X 1)
=
х
–
х 2
=
х(1-
х)
=
pq. Хэрэв X k – үйл явдлын тохиолдлын тоо Атэгээд аль шалгалтанд Р(X руу)=
ρ
Тэгээд X=X 1 +X 2 +….+X n . Эндээс бид авдаг М(X)=М(X 1
)+М(X 2)+
… +М(X n)=
nρ,
Д(X)=Д(X 1)+Д(X 2)+
...
+Д(X n)=npq. 4.7.
Чанарын хяналтын хэлтэс нь бүтээгдэхүүний стандартыг шалгадаг. Бүтээгдэхүүн нь стандарт байх магадлал 0.9 байна. Багц бүр 5 бүтээгдэхүүнтэй. Дискрет санамсаргүй хэмжигдэхүүний математик хүлээлтийг ол X- тус бүр нь 4 стандарт бүтээгдэхүүн агуулсан багцын тоо - хэрэв 50 багцад хяналт шалгалт хийх юм бол. Шийдэл. Санамсаргүй байдлаар сонгосон багц бүрт 4 стандарт бүтээгдэхүүн байх магадлал тогтмол; гэж тэмдэглэе ρ
.Дараа нь санамсаргүй хэмжигдэхүүний математик хүлээлт Xтэнцүү байна М(X)=
50∙ρ.
Магадлалыг олъё ρ
Бернуллигийн томъёоны дагуу: ρ=P 5 (4)= М(X)=
50∙0,32=16. 4.8
. Гурван шоо шидэв. Унасан онооны нийлбэрийн математик хүлээлтийг ол. Шийдэл.Та санамсаргүй хэмжигдэхүүний тархалтыг олж болно X- буурсан онооны нийлбэр, дараа нь түүний математик хүлээлт. Гэсэн хэдий ч энэ зам хэтэрхий төвөгтэй юм. Санамсаргүй хэмжигдэхүүнийг төлөөлөх өөр техникийг ашиглах нь илүү хялбар байдаг X, математикийн хүлээлтийг тооцоолоход хялбар хэд хэдэн энгийн санамсаргүй хэмжигдэхүүнүүдийн нийлбэр хэлбэрээр тооцоолох шаардлагатай. Хэрэв санамсаргүй хэмжигдэхүүн X би- энэ бол унасан онооны тоо юм би- яс ( би= 1, 2, 3), дараа нь онооны нийлбэр Xхэлбэрээр илэрхийлэгдэх болно X = X 1 + X 2 + X 3 . Анхны санамсаргүй хэмжигдэхүүний математик хүлээлтийг тооцоолохын тулд зөвхөн математикийн хүлээлтийн шинж чанарыг ашиглахад л үлддэг. М(X 1
+ X 2 + X 3
)= М(X 1
)+ М(X 2)+ М(X 3
). Энэ нь ойлгомжтой Р(X би = К)=
1/6, TO=
1, 2, 3, 4, 5, 6,
би=
1,
2, 3. Тиймээс санамсаргүй хэмжигдэхүүний математик хүлээлт X бишиг харагдаж байна М(X би)
=
1/6∙1
+ 1/6∙2
+1/6∙3
+ 1/6∙4
+ 1/6∙5
+ 1/6∙6
= 7/2, М(X)
=
3∙7/2 = 10,5.
4.9.
Туршилтын явцад бүтэлгүйтсэн төхөөрөмжүүдийн тооны математик хүлээлтийг тодорхойлно уу: a) бүх төхөөрөмжийн эвдрэлийн магадлал ижил байна Р, мөн туршилтад байгаа төхөөрөмжүүдийн тоо тэнцүү байна n; б) бүтэлгүйтлийн магадлал би
–
төхөөрөмжийн хэмжээ тэнцүү байна х би
,
би=
1,
2, … , n. Шийдэл.Санамсаргүй хэмжигдэхүүнийг үзье XЭнэ нь бүтэлгүйтсэн төхөөрөмжүүдийн тоо юм X = X 1 + X 2 + … + X n ,
X би
=
Энэ нь ойлгомжтой Р(X би =
1)=
Р би ,
Р(X би =
0)=
1–
Р би ,i= 1,
2,
…
,n. М(X би)=
1∙Р би +
0∙(1-Р би)=П би , М(X)=М(X 1)+М(X 2)+ … +М(X n)=П 1 +П 2 + … + П n .
"a" тохиолдолд төхөөрөмжийн эвдрэлийн магадлал ижил байна, өөрөөр хэлбэл Р би =p,i= 1,
2, …
,n. М(X)=
n.p.. Хэрэв бид санамсаргүй хэмжигдэхүүн байгааг анзаарсан бол энэ хариултыг шууд авах боломжтой Xпараметртэй бином тархалттай ( n,
х).
4.10.
Хоёр шоо нэгэн зэрэг хоёр удаа шиддэг. Дискрет санамсаргүй хэмжигдэхүүний тархалтын хоёр гишүүний хуулийг бич X -хоёр шоо дээрх тэгш тооны онооны өнхрөх тоо. Шийдэл. Болъё А=(эхний шоо дээр тэгш тоог өнхрүүлэх), B =(хоёр дахь шоо дээр тэгш тоог өнхрүүлэх). Нэг шидэлтээр хоёр шоо дээр тэгш тоо гарах нь бүтээгдэхүүнээр илэрхийлэгдэнэ AB.Дараа нь Р
(AB)
= Р(А)∙Р(IN)
=
Хоёр шоо хоёр дахь шидэлтийн үр дүн эхнийхээс хамаарахгүй тул Бернуллигийн томъёог дараах үед хэрэглэнэ. n
=
2,p = 1/4,
q
=
1– p = 3/4.
Санамсаргүй утга X 0, 1, 2 утгыг авч болно ,
Үүний магадлалыг Бернуллигийн томъёог ашиглан олж болно. Р(X= 0)= П 2
(0)
=
q
2
= 9/16, Р(X= 1)= П 2
(1)= C Р(X= 2)= П 2
(2)= C Санамсаргүй хэмжигдэхүүний тархалтын цуваа X: 4.11.
Энэхүү төхөөрөмж нь олон тооны бие даасан ажиллагаатай элементүүдээс бүрддэг бөгөөд элемент бүр нь цаг хугацааны явцад эвдрэх магадлал маш бага байдаг. т. Цаг хугацаа өнгөрөхөд татгалзсан дундаж тоог ол тэлементүүд, хэрэв энэ хугацаанд ядаж нэг элемент бүтэлгүйтэх магадлал 0.98 бол. Шийдэл.
Цаг хугацаа өнгөрөхөд татгалзсан хүмүүсийн тоо тэлементүүд - санамсаргүй хэмжигдэхүүн X, энэ нь Пуассоны хуулийн дагуу тархсан, элементийн тоо их байдаг тул элементүүд нь бие даан ажилладаг бөгөөд элемент бүрийн эвдрэлийн магадлал бага байдаг. -д тохиолдсон үйл явдлын дундаж тоо nтестүүд тэнцүү байна М(X)
=
n.p..
Амжилтгүй болох магадлалаас хойш TO-аас элементүүд nтомъёогоор илэрхийлнэ Р n
(TO)
хаана
=
n.p., дараа нь тухайн хугацаанд нэг ч элемент бүтэлгүйтэх магадлал т
бид хүрдэг K = 0: Р n
(0)= e - . Тиймээс эсрэг үйл явдлын магадлал нь цаг хугацааны хувьд юм т
дор хаяж нэг элемент амжилтгүй болсон - 1-тэй тэнцүү - д -
. Асуудлын нөхцлийн дагуу энэ магадлал 0.98 байна. Eq-аас. 1
- д -
= 0,98, д -
= 1 – 0,98 =
0,02, эндээс
=
-ln
0,02
4. Тиймээс, цаг тухайд нь ттөхөөрөмжийн ажиллагаа, дунджаар 4 элемент амжилтгүй болно. 4.12
. Шоонуудыг "хоёр" гарч ирэх хүртэл шиднэ. Шидэлтийн дундаж тоог ол. Шийдэл. Санамсаргүй хэмжигдэхүүнийг танилцуулъя X– бидний сонирхсон үйл явдал болох хүртэл хийх ёстой шинжилгээний тоо. Тийм магадлал X= 1 нь шоо нэг шидэхэд "хоёр" гарч ирэх магадлалтай тэнцүү, өөрөөр хэлбэл. Р(X= 1)
= 1/6. Үйл явдал X= 2 гэдэг нь эхний шалгалтанд "хоёр" нь унасангүй, харин хоёр дахь удаагаа унасан гэсэн үг. Үйл явдлын магадлал X= 2-ыг бие даасан үйл явдлын магадлалыг үржүүлэх дүрмээр олно. Р(X= 2)
= (5/6)∙(1/6) Үүний нэгэн адил, Р(X= 3)
= (5/6) 2 ∙1/6, Р(X= 4)
= (5/6) 2 ∙1/6 гэх мэт. Бид хэд хэдэн магадлалын хуваарилалтыг олж авдаг: (5/6) руу
∙1/6 Шидэлтийн дундаж тоо (туршилт) нь математикийн хүлээлт юм М(X)
=
1∙1/6 +
2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6
+ … + TO
(5/6) TO -1 ∙1/6
+ … = 1/6∙(1+2∙5/6 +3∙(5/6) 2
+ … + TO
(5/6) TO -1
+ …) Цувралын нийлбэрийг олъё: Тиймээс, М(X)
=
(1/6) (1/ (1 –
5/6) 2
= 6. Тиймээс та "хоёр" гарч ирэх хүртэл дунджаар 6 шоо шидэх хэрэгтэй. 4.13.
Бие даасан туршилтыг үйл явдал тохиолдох магадлалын адилаар явуулдаг Ашалгалт бүрт. Үйл явдал болох магадлалыг ол А, хэрэв гурван бие даасан туршилтын явцад тохиолдсон үйл явдлын тооны хэлбэлзэл 0.63 бол .
Шийдэл.Гурван туршилтын явцад тохиолдсон үйл явдлын тоо нь санамсаргүй хэмжигдэхүүн юм X, бином хуулийн дагуу тархсан. Бие даасан туршилтын явцад тохиолдсон үйл явдлын тооны хэлбэлзэл (туршилт бүрт үйл явдал тохиолдох магадлал ижил) нь тухайн үйл явдал тохиолдох ба тохиолдохгүй байх магадлалаар туршилтын тоог үржүүлсэнтэй тэнцүү байна. (асуудал 4.6) Д(X)
=
npq.
Нөхцөлөөр n
=
3,
Д(X)
=
0.63, тэгэхээр та чадна Ртэгшитгэлээс олно 0,63
= 3∙Р(1-Р), хоёр шийдэлтэй Р 1
=
0.7 ба Р 2
=
0,3.

 1.2.
p4=0.1; x≤-1 үед 0,
1.2.
p4=0.1; x≤-1 үед 0,

 (Зураг 5)
(Зураг 5) https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> x≤a-д 0,
https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> x≤a-д 0, ,
, Ердийн муруй нь x=m шулуунтай харьцуулахад тэгш хэмтэй, x=a үед хамгийн их утгатай, тэнцүү байна.
Ердийн муруй нь x=m шулуунтай харьцуулахад тэгш хэмтэй, x=a үед хамгийн их утгатай, тэнцүү байна.
![]() ,
,![]()
![]()

Шийдэл.
Төрийн сүлд зураагүй байх магадлал: P(0) = 0.5*0.5*0.5= 0.125
P(1) = 0,5
*0,5*0,5 + 0,5*0,5
*0,5 + 0,5*0,5*0,5
= 3*0,125=0,375
P(2) = 0,5
*0,5
*0,5 + 0,5
*0,5*0,5
+ 0,5*0,5
*0,5
= 3*0,125=0,375
Гурван сүлд авах магадлал: P(3) = 0.5*0.5*0.5 = 0.125
Шалгах: P = P(0) + P(1) + P(2) + P(3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 X 0
1
2
3
П 0,125
0,375
0,375
0,125
Шийдэл.
А үйл явдлыг авч үзье - зорилтот нэг цохилт. Энэ үйл явдал тохиолдох боломжит хувилбарууд нь дараах байдалтай байна.
Дараа нь А үйл явдлын магадлал – байг яг нэг удаа цохих нь: P(A) = 0.12+0.17+0.68 = 0.97 байх болно. ![]() , түүгээр санамсаргүй хэмжигдэхүүн нь утга тус бүрийг авдаг, i.e.
, түүгээр санамсаргүй хэмжигдэхүүн нь утга тус бүрийг авдаг, i.e. ![]() .
.Утга
...
Магадлал
...
![]() нийцэхгүй бөгөөд цорын ганц боломжтой: тэдгээр нь үйл явдлын бүрэн системийг бүрдүүлдэг. Тиймээс тэдний магадлалын нийлбэр нэгтэй тэнцүү байна.
нийцэхгүй бөгөөд цорын ганц боломжтой: тэдгээр нь үйл явдлын бүрэн системийг бүрдүүлдэг. Тиймээс тэдний магадлалын нийлбэр нэгтэй тэнцүү байна.![]() .
.Ялалтын хэмжээ -100
900
2900
Магадлал 0,94
0,04
0,02
Дискрет санамсаргүй хэмжигдэхүүний тархалтын функц: барилга
![]() , энэ нь санамсаргүй хэмжигдэхүүний утгын магадлалыг тодорхойлдог Xхязгаарын утгаас бага буюу тэнцүү байна X.
, энэ нь санамсаргүй хэмжигдэхүүний утгын магадлалыг тодорхойлдог Xхязгаарын утгаас бага буюу тэнцүү байна X.Утга 1
2
3
4
5
6
Магадлал 1/6
1/6
1/6
1/6
1/6
1/6

Утга 0
1
2
3
Магадлал 1/30
3/10
1/2
1/6
![]() . At
. At
Дискрет санамсаргүй хэмжигдэхүүний тархалтын функц: тооцоо
Гэрлэлтийн үргэлжлэх хугацаа (жил) Тоо Магадлал Ф(x)
0
10
0,002
0,002
1
80
0,013
0,015
2
177
0,029
0,044
3
209
0,035
0,079
4
307
0,051
0,130
5
335
0,056
0,186
6
358
0,060
0,246
7
413
0,069
0,314
8
432
0,072
0,386
9
402
0,067
0,453
10 ба түүнээс дээш 3287
0,547
1,000
Нийт 6010
1
Дискрет санамсаргүй хэмжигдэхүүний тархалтын хууль ба математикийн хүлээлт ба дисперсийн хоорондын хамаарал
 (1)
(1)
![]() , (2)
, (2)![]() .
.![]()

![]() ,
,



ХЭРЭГЛЭЭ
Комбинаторикийн элементүүд

Үйл явдал дээрх үйлдлүүд
 ;
; ;
;
Магадлалын сонгодог тодорхойлолт
 , үйл явдал тохиолдоход таатай А, туршилтын нийт тоонд
, үйл явдал тохиолдоход таатай А, туршилтын нийт тоонд  :
:
Магадлалын үржүүлэх томъёо
 томъёог ашиглан олж болно:
томъёог ашиглан олж болно: - үйл явдлын магадлал А,
- үйл явдлын магадлал А, - үйл явдлын магадлал IN,
- үйл явдлын магадлал IN, - үйл явдлын магадлал INүйл явдал болсон тохиолдолд Ааль хэдийн болсон.
- үйл явдлын магадлал INүйл явдал болсон тохиолдолд Ааль хэдийн болсон.
Магадлал нэмэх томъёо
 томъёог ашиглан олж болно:
томъёог ашиглан олж болно: - үйл явдлын хамт тохиолдох магадлал АТэгээд IN.
- үйл явдлын хамт тохиолдох магадлал АТэгээд IN.
Нийт магадлалын томъёо
 ,
,
 ,
…,
,
…,
 - тэдгээрийг таамаглал гэж нэрлэе. Мөн мэдэгдэж байна
- тэдгээрийг таамаглал гэж нэрлэе. Мөн мэдэгдэж байна  - гүйцэтгэлийн магадлал би-р таамаглал ба
- гүйцэтгэлийн магадлал би-р таамаглал ба  - гүйцэтгэх үед А үйл явдал тохиолдох магадлал би-р таамаглал. Дараа нь үйл явдлын магадлал Атомъёогоор олж болно:
- гүйцэтгэх үед А үйл явдал тохиолдох магадлал би-р таамаглал. Дараа нь үйл явдлын магадлал Атомъёогоор олж болно:
Бернулли схем

 Бернулли схемд энэ нь хамгийн өндөр магадлалтай тодорхой үйл явдлын тохиолдлын тоо юм. Томъёог ашиглан олж болно:
Бернулли схемд энэ нь хамгийн өндөр магадлалтай тодорхой үйл явдлын тохиолдлын тоо юм. Томъёог ашиглан олж болно:
Санамсаргүй хувьсагч
Дискрет санамсаргүй хэмжигдэхүүний тоон шинж чанар
X



Р



Түгээлтийн функц
Шалгалтанд зориулсан асуултууд

 .
.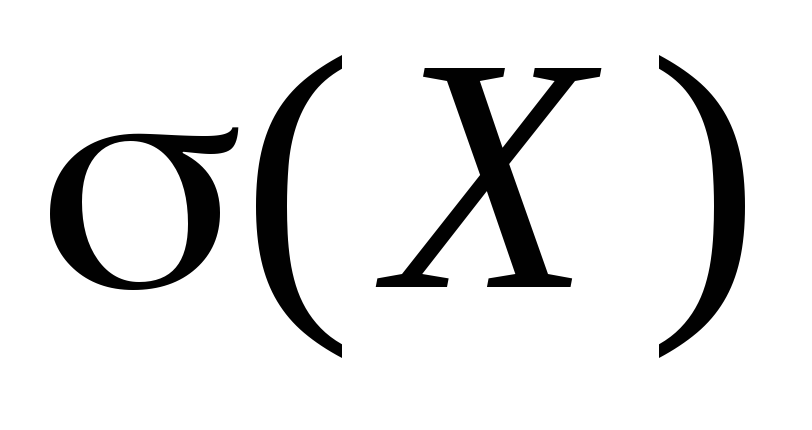 .
. ,
, 0,3(0,7) 2
= 0,441,
0,3(0,7) 2
= 0,441, (0,3) 2 0,7
= 0,189,
(0,3) 2 0,7
= 0,189,

 .
.
 .
. .
.

 ,
,
 ,Р 2 (1)
=
,Р 2 (1)
= ∙
∙ ,Р 2 (2)
=
,Р 2 (2)
=
 =1/5,
=1/5, = 3/5,
= 3/5, = 1/5.
= 1/5.
 ρ
руу
(1-ρ
) n-руу
ρ
руу
(1-ρ
) n-руу
 ρq n- 1
ρq n- 1
 ρq n- 2
ρq n- 2
 ρ
n
ρ
n ρq n -
1
+2
ρq n -
1
+2
 ρ
2
q n -
2
+…+.n
ρ
2
q n -
2
+…+.n
 ρ
n
ρ
n
 = 0,94∙0,1=0,32.
= 0,94∙0,1=0,32.
 .
. ,Р∙q
=
6/16,
,Р∙q
=
6/16, ,
Р 2
=
1/16.
,
Р 2
=
1/16.
 ,
,
 TOg
TO -1
= (
TOg
TO -1
= ( g TO)
g
g TO)
g
 .
.







