වෙනත් ශබ්ද කෝෂවල "කොන්දේසි අන්තය" යනු කුමක්දැයි බලන්න:

සාපේක්ෂ අන්තය, n + m විචල්‍යවල f (x1,..., xn + m) ශ්‍රිතයේ අන්තය, මෙම විචල්‍යයන් m වැඩි සම්බන්ධක සමීකරණවලට (කොන්දේසි) යටත් වේ යැයි උපකල්පනය කරමින්: φk (x1,..., xn + m) = 0, 1≤ k ≤ m (*) (අන්තය බලන්න)… …

විවෘත කට්ටලයක් සහ ක්‍රියාකාරීත්වය ලබා දීමට ඉඩ දෙන්න. ඉඩ. මෙම සමීකරණ සීමා සමීකරණ ලෙස හැඳින්වේ (පාරිභාෂිතය යාන්ත්‍ර විද්‍යාවෙන් ණයට ගෙන ඇත). G ... Wikipedia හි ශ්‍රිතයක් අර්ථ දැක්වීමට ඉඩ දෙන්න

- (ලතින් අන්ත අන්තයෙන්) අඛණ්ඩ ශ්‍රිතයක අගය f (x), එය උපරිම හෝ අවම වේ. වඩාත් නිවැරදිව: x0 ලක්ෂ්‍යයේ f (x) සන්තතික ශ්‍රිතයක් මෙම ලක්ෂ්‍යයේ අසල්වැසි ප්‍රදේශයක් (x0 + δ, x0 δ) තිබේ නම්, x0 හි උපරිම (අවම) ඇත, ... ... මහා සෝවියට් විශ්වකෝෂය

මෙම පදයට වෙනත් අර්ථයන් ඇත, අන්ත (අර්ථ) බලන්න. ගණිතයේ Extremum (ලතින් අන්ත අන්ත) යනු දී ඇති කට්ටලයක ශ්‍රිතයක උපරිම හෝ අවම අගයයි. අන්තයට ළඟා වන ලක්ෂ්‍යය වන්නේ ... ... විකිපීඩියාවයි

විචල්‍ය සහ ක්‍රියාකාරී කිහිපයක කොන්දේසි සහිත ශ්‍රිතයක් සඳහා ගැටළු විසඳීම සඳහා භාවිතා කරන ශ්‍රිතයකි. එල් එෆ් ආධාරයෙන්. කොන්දේසි සහිත අන්තයක් සඳහා අවශ්‍ය ප්‍රශස්ත තත්වයන් ගැටළු වල ලියා ඇත. විචල්‍ය පමණක් ප්‍රකාශ කිරීමට අවශ්‍ය නැත... ගණිතමය විශ්වකෝෂය

ශ්‍රිත එකක් හෝ කිහිපයක් තෝරා ගැනීම මත පදනම්ව විචල්‍යවල ක්‍රියාකාරීත්වයේ ආන්තික (උපරිම සහ අවම) අගයන් සෙවීමට කැප වූ ගණිතමය විෂයයකි. සහ. එය එම පරිච්ඡේදයේ ස්වභාවික වර්ධනයකි.... මහා සෝවියට් විශ්වකෝෂය

කොන්දේසි සහිත අන්තයක් සඳහා ගැටළු අධ්‍යයනය කිරීමේදී Lagrange ශ්‍රිතය ගොඩනගා ඇති විචල්‍යයන්. L. m. සහ Lagrange ශ්‍රිතය භාවිතා කිරීම කොන්දේසි සහිත අන්තයක් සඳහා වන ගැටළු වලදී ඒකාකාරී ආකාරයෙන් අවශ්‍ය ප්‍රශස්ත තත්වයන් ලබා ගැනීමට හැකි වේ ... ගණිතමය විශ්වකෝෂය

වෙනස්කම් පිළිබඳ කලනය යනු ක්‍රියාකාරීත්වයේ විචලනයන් අධ්‍යයනය කරන ක්‍රියාකාරී විශ්ලේෂණයේ ශාඛාවකි. විචලනයන් ගණනය කිරීමේ වඩාත් සාමාන්‍ය කාර්යය වන්නේ දී ඇති ක්‍රියාකාරීත්වයක් ළඟා වන ශ්‍රිතයක් සොයා ගැනීමයි ... ... විකිපීඩියා

මේවාට පනවා ඇති විවිධ ආකාරයේ සීමා කිරීම් (අදියර, අවකලනය, අනුකලනය, ආදිය) යටතේ ශ්‍රිත එකක් හෝ කිහිපයක් තෝරා ගැනීම මත රඳා පවතින ක්‍රියාකාරීත්වයේ අන්තය සොයා ගැනීමේ ක්‍රම අධ්‍යයනයට කැප වූ ගණිත අංශයකි ... ... ගණිතමය විශ්වකෝෂය

වෙනස්කම් පිළිබඳ කලනය යනු ක්‍රියාකාරීත්වයේ වෙනස්කම් අධ්‍යයනය කරන ගණිත අංශයකි. විචලනයන් ගණනය කිරීමේ වඩාත් සාමාන්‍ය කාර්යය වන්නේ ක්‍රියාකාරීත්වය ආන්තික අගයකට ළඟා වන ශ්‍රිතයක් සොයා ගැනීමයි. ක්රම ... ... විකිපීඩියාව

පොත්

• පාලන න්‍යාය පිළිබඳ දේශන. වෙළුම 2. Optimal Control, V. Boss. ප්රශස්ත පාලනය පිළිබඳ න්යායේ සම්භාව්ය ගැටළු සලකා බලනු ලැබේ. ඉදිරිපත් කිරීම ආරම්භ වන්නේ පරිමිත-මාන අවකාශයන්හි ප්‍රශස්තකරණය පිළිබඳ මූලික සංකල්ප සමඟිනි: කොන්දේසි සහිත සහ කොන්දේසි විරහිත අන්ත, ...

අර්ථ දැක්වීම 1: කිසියම් ලක්ෂ්‍යයක් සඳහා එම ලක්ෂ්‍යයේ අසල්වැසි ප්‍රදේශයක් තිබේ නම්, ශ්‍රිතයකට ලක්ෂ්‍යයක දේශීය උපරිමයක් ඇතැයි කියනු ලැබේ. එම්ඛණ්ඩාංක සමඟ (x, y)අසමානතාවය සපුරා ඇත: මෙම අවස්ථාවෙහිදී, එනම්, ශ්රිතයේ වැඩිවීම< 0.

අර්ථ දැක්වීම2: ඕනෑම ලක්ෂ්‍යයක් සඳහා ලක්ෂ්‍යයේ අසල්වැසි ප්‍රදේශයක් තිබේ නම්, ශ්‍රිතයකට ලක්ෂ්‍යයක දේශීය අවමයක් ඇතැයි කියනු ලැබේ. එම්ඛණ්ඩාංක සමඟ (x, y)අසමානතාවය සපුරා ඇත: මෙම අවස්ථාවෙහිදී, එනම්, ශ්‍රිතයේ වැඩිවීම > 0.

අර්ථ දැක්වීම 3: තිත් දේශීය අවමසහ උපරිම ලෙස හැඳින්වේ අන්ත ලකුණු.

කොන්දේසි සහිත අන්ත

බොහෝ විචල්‍යවල ශ්‍රිතයක අන්ත සෙවීමේදී, බොහෝ විට ඊනියා සම්බන්ධ ගැටළු පැන නගී කොන්දේසි සහිත අන්ත.මෙම සංකල්පය විචල්‍ය දෙකක ශ්‍රිතයක උදාහරණයකින් පැහැදිලි කළ හැක.

ශ්‍රිතයක් සහ රේඛාවක් ලබා දෙන්න එල්මතුපිටින් 0xy. කර්තව්යය වන්නේ රේඛාවයි එල්එවැනි කරුණක් සොයා ගන්න P(x, y),රේඛාවේ ලක්ෂ්‍යවල මෙම ශ්‍රිතයේ අගයන්ට සාපේක්ෂව ශ්‍රිතයේ අගය විශාලතම හෝ කුඩාම වේ එල්ලක්ෂ්යය අසල පිහිටා ඇත පී. එවැනි කරුණු පීකියලා කොන්දේසි සහිත අන්ත ලකුණුරේඛීය කාර්යයන් එල්. සාමාන්‍ය අන්ත ලක්ෂ්‍යය මෙන් නොව, කොන්දේසි සහිත අන්ත ලක්ෂ්‍යයේ ක්‍රියාකාරී අගය සංසන්දනය කරනු ලබන්නේ එහි සමහර අසල්වැසි ස්ථානවල සියලුම ස්ථානවල නොව, රේඛාවේ ඇති ස්ථානවල පමණි. එල්.

සුපුරුදු අන්තයේ ලක්ෂ්‍යය බව ඉතා පැහැදිලිය (ඔවුන් ද කියයි කොන්දේසි විරහිත අන්තය) යනු මෙම ලක්ෂ්‍යය හරහා ගමන් කරන ඕනෑම රේඛාවක් සඳහා කොන්දේසි සහිත අන්ත ලක්ෂ්‍යයකි. ප්රතිලෝම, ඇත්ත වශයෙන්ම, සත්ය නොවේ: කොන්දේසි සහිත අන්ත ලක්ෂ්යයක් සාම්ප්රදායික අන්ත ලක්ෂ්යයක් නොවිය හැක. මම මෙය සරල උදාහරණයකින් පැහැදිලි කරන්නම්. ශ්රිතයේ ප්රස්ථාරය ඉහළ අර්ධගෝලය (උපග්රන්ථය 3 (රූපය 3)) වේ.

මෙම ශ්‍රිතයේ මූලාරම්භයේ උපරිමයක් ඇත; එය ඉහළට අනුරූප වේ එම්අර්ධගෝල. රේඛාව නම් එල්ලකුණු හරහා ගමන් කරන රේඛාවක් තිබේ නමුත්හා හිදී(ඇගේ සමීකරණය x+y-1=0), එවිට මෙම රේඛාවේ ලක්ෂ්ය සඳහා බව ජ්යාමිතිකව පැහැදිලි වේ ඉහළම අගයලක්ෂ්‍ය අතර මැද පිහිටි ලක්ෂ්‍යයකට ශ්‍රිතය ළඟා වේ නමුත්හා හිදී.ලබා දී ඇති රේඛාවේ ශ්‍රිතයේ කොන්දේසි සහිත අන්තයේ (උපරිම) ලක්ෂ්‍යය මෙයයි; එය අර්ධගෝලයේ M 1 ලක්ෂ්‍යයට අනුරූප වන අතර, මෙහි සාමාන්‍ය අන්තයක් පිළිබඳ ප්‍රශ්නයක් තිබිය නොහැකි බව රූපයෙන් දැකිය හැකිය.

සංවෘත කලාපයක ශ්‍රිතයක විශාලතම හා කුඩාම අගයන් සෙවීමේ ගැටලුවේ අවසාන කොටසේදී, මෙම කලාපයේ මායිමේ ශ්‍රිතයේ ආන්තික අගයන් අපට සොයාගත යුතු බව සලකන්න, එනම්. යම් රේඛාවක් මත, සහ එමගින් කොන්දේසි සහිත අන්තයක් සඳහා ගැටළුව විසඳන්න.

අපි දැන් Z= f(x, y) ශ්‍රිතයේ කොන්දේසි සහිත අන්තයේ ලක්ෂ්‍ය සඳහා ප්‍රායෝගික සෙවීමට යමු, x සහ y විචල්‍යයන් x සහ y සමීකරණයෙන් (x, y) = 0 සම්බන්ධ වේ. මෙම සම්බන්ධතාවය වනුයේ සීමා සමීකරණය ලෙස හැඳින්වේ. සම්බන්ධතා සමීකරණයෙන් y x: y \u003d (x) අනුව පැහැදිලිව ප්‍රකාශ කළ හැකි නම්, අපට Z \u003d f (x, (x)) \u003d Ф (x) එක් විචල්‍යයක ශ්‍රිතයක් ලැබේ.

මෙම ශ්‍රිතය අන්තයකට ළඟා වන x හි අගය සොයා ගැනීමෙන් පසුව, සම්බන්ධතා සමීකරණයෙන් y හි අනුරූප අගයන් තීරණය කිරීමෙන්, අපි කොන්දේසි සහිත අන්තයේ අපේක්ෂිත ලකුණු ලබා ගනිමු.

ඉතින්, ඉහත උදාහරණයේ, x+y-1=0 සන්නිවේදන සමීකරණයෙන් අපට y=1-x ලැබේ. මෙතැන් සිට

z එහි උපරිමයට x = 0.5 ට ළඟා වන බව පරීක්ෂා කිරීම පහසුය; නමුත් පසුව සම්බන්ධක සමීකරණයෙන් y = 0.5, සහ අපි හරියටම P ලක්ෂ්යය ලබා ගනිමු, ජ්යාමිතික සලකා බැලීම් වලින් සොයාගත හැකිය.

සීමාකාරී සමීකරණය නිරූපණය කළ හැකි විට පවා කොන්දේසි සහිත අන්තයක් සඳහා ගැටළුව ඉතා සරලව විසඳනු ලැබේ පරාමිතික සමීකරණ x=x(t), y=y(t). x සහ y සඳහා ප්‍රකාශන ආදේශ කිරීම මෙම කාර්යය, අපි නැවතත් එක් විචල්‍යයක ශ්‍රිතයක අන්තය සෙවීමේ ගැටලුවට පැමිණෙමු.

සීමා සමීකරණයට වඩා වැඩි නම් සංකීර්ණ දර්ශනයසහ අපට එක් විචල්‍යයක් තවත් විචල්‍යයක් අනුව පැහැදිලිව ප්‍රකාශ කිරීමට හෝ එය පරාමිතික සමීකරණ සමඟ ප්‍රතිස්ථාපනය කිරීමට නොහැකි වේ, එවිට කොන්දේසි සහිත අන්තයක් සොයා ගැනීමේ ගැටලුව වඩාත් අපහසු වේ. අපි දිගටම උපකල්පනය කරමු z= f(x, y) ශ්‍රිතයේ ප්‍රකාශනයේ විචල්‍යය (x, y) = 0. z= f(x, y) ශ්‍රිතයේ සම්පූර්ණ ව්‍යුත්පන්නය සමාන වන්නේ:

අවකලනය පිළිබඳ රීතිය මගින් සොයා ගන්නා ලද y` ව්‍යුත්පන්නය කොහිද? ව්යංග කාර්යය. කොන්දේසි සහිත අන්තයේ ලක්ෂ්‍යවලදී, සොයාගත් සම්පූර්ණ ව්‍යුත්පන්නය ශුන්‍යයට සමාන විය යුතුය; මෙය x සහ y සම්බන්ධ එක් සමීකරණයක් ලබා දෙයි. ඒවා සීමා සමීකරණය ද තෘප්තිමත් කළ යුතු බැවින්, අපට නොදන්නා දෙකක් සහිත සමීකරණ දෙකක පද්ධතියක් ලැබේ.

පළමු සමීකරණය සමානුපාතික ලෙස ලිවීමෙන් සහ නොදන්නා නව සහායකයක් හඳුන්වා දීමෙන් මෙම පද්ධතිය වඩාත් පහසු එකක් බවට පරිවර්තනය කරමු:

(පහසුව සඳහා ඍණ ලකුණක් ඉදිරියෙන් තබා ඇත). මෙම සමානාත්මතාවයෙන් පහත පද්ධතියට ගමන් කිරීම පහසුය:

f` x =(x,y)+` x (x,y)=0, f` y (x,y)+` y (x,y)=0 (*),

එය, සීමා සමීකරණය (x, y) = 0 සමඟ එක්ව, නොදන්නා x, y, සහ සමඟ සමීකරණ තුනක පද්ධතියක් සාදයි.

මෙම සමීකරණ (*) භාවිතා කිරීම මතක තබා ගැනීමට පහසුම වේ ඊළඟ රීතිය: ශ්‍රිතයේ කොන්දේසි සහිත අන්තයේ ලක්ෂ්‍ය විය හැකි ලක්ෂ්‍ය සොයා ගැනීම සඳහා

Z= f(x, y) සීමා සමීකරණය සමඟ (x, y) = 0, ඔබට සහායක ශ්‍රිතයක් සෑදිය යුතුය

F(x,y)=f(x,y)+(x,y)

යම් නියතයක් ඇති තැන, සහ මෙම ශ්‍රිතයේ අන්ත ලක්ෂ්‍ය සොයා ගැනීමට සමීකරණ ලියන්න.

නිශ්චිත සමීකරණ පද්ධතිය රීතියක් ලෙස, අවශ්ය කොන්දේසි පමණක් ලබා දෙයි, i.e. මෙම පද්ධතිය තෘප්තිමත් කරන සෑම x සහ y අගයන් යුගලයක්ම අනිවාර්යයෙන්ම කොන්දේසි සහිත අන්ත ලක්ෂ්‍යයක් නොවේ. මම කොන්දේසි සහිත අන්ත ලකුණු සඳහා ප්රමාණවත් කොන්දේසි ලබා නොදෙනු ඇත; බොහෝ විට ගැටලුවේ නිශ්චිත අන්තර්ගතයම සොයාගත් කරුණ කුමක්දැයි යෝජනා කරයි. කොන්දේසි සහිත අන්තයක් සඳහා ගැටළු විසඳීම සඳහා විස්තර කරන ලද තාක්ෂණය Lagrange ගුණක ක්රමය ලෙස හැඳින්වේ.

අපි මුලින්ම විචල්‍ය දෙකක ශ්‍රිතයක් ගැන සලකා බලමු. $M_0(x_0;y_0)$ ලක්ෂ්‍යයේ $z=f(x,y)$ ශ්‍රිතයේ කොන්දේසිගත අන්තය මෙම ශ්‍රිතයේ අන්තය වන අතර, $x$ සහ $y$ යන විචල්‍යයන් යටතේ ළඟා වේ. මෙම ලක්ෂ්‍යයට ආසන්නව $\ varphi(x,y)=0$ සීමා සමීකරණය තෘප්තිමත් කරයි.

"කොන්දේසි" අන්තය යන නම ලැබී ඇත්තේ විචල්‍යයන් පනවන බැවිනි අතිරේක කොන්දේසිය$\varphi(x,y)=0$. සම්බන්ධතා සමීකරණයෙන් එක් විචල්‍යයක් තවත් විචල්‍යයක් අනුව ප්‍රකාශ කළ හැකි නම්, කොන්දේසිගත අන්තය තීරණය කිරීමේ ගැටලුව එක් විචල්‍යයක ශ්‍රිතයක සාමාන්‍ය අන්තයේ ගැටලුව දක්වා අඩු වේ. උදාහරණයක් ලෙස, $y=\psi(x)$ සීමා සමීකරණයෙන් අනුගමනය කරන්නේ නම්, $y=\psi(x)$ $z=f(x,y)$ ලෙස ආදේශ කළහොත්, අපට $ එක විචල්‍යයක ශ්‍රිතයක් ලැබේ. z=f\වම (x,\psi(x)\දකුණ)$. හිදී සාමාන්ය නඩුව, කෙසේ වෙතත්, මෙම ක්‍රමය එතරම් ප්‍රයෝජනයක් නැත, එබැවින් නව ඇල්ගොරිතමයක් අවශ්‍ය වේ.

විචල්‍ය දෙකක ශ්‍රිත සඳහා Lagrange ගුණක ක්‍රමය.

Lagrange ගුණකවල ක්‍රමය නම් කොන්දේසි සහිත අන්තය සොයා ගැනීම සඳහා Lagrange ශ්‍රිතය සමන්විත වේ: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ ($\lambda පරාමිතිය $ Lagrange ගුණකය ලෙස හැඳින්වේ ). නිශ්චල ලක්ෂ්‍ය තීරණය කරනු ලබන සමීකරණ පද්ධතියක් මගින් අවශ්‍ය අන්ත තත්වයන් ලබා දෙනු ලැබේ:

$$ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \varphi (x,y)=0.\අවසන්(පෙළගැසී)\දකුණ.$$

ලකුණ $d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("" )dy^2$. ස්ථාවර ලක්ෂ්‍යයක $d^2F > 0$ නම්, $z=f(x,y)$ ශ්‍රිතයට මෙම අවස්ථාවේදී කොන්දේසි සහිත අවම අගයක් ඇත, නමුත් $d^2F නම්< 0$, то условный максимум.

අන්තයේ ස්වභාවය තීරණය කිරීමට තවත් ක්රමයක් තිබේ. සීමා සමීකරණයෙන් අපට ලැබෙන්නේ: $\varphi_(x)^(")dx+\varphi_(y)^(")dy=0$, $dy=-\frac(\varphi_(x)^("))( \varphi_ (y)^("))dx$, එබැවින් ඕනෑම නිශ්චල ලක්ෂ්‍යයක අපට ඇත්තේ:

$$d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=F_(xx)^( "")dx^2+2F_(xy)^("")dx\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\ right)+ F_(yy)^("")\වම(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)^2=\\ =-\frac (dx^2)(\left(\varphi_(y)^(") \right)^2)\cdot\left(-(\varphi_(y)^("))^2 F_(xx)^(" ")+2\varphi_(x)^(")\varphi_(y)^(")F_(xy)^("")-(\varphi_(x)^("))^2 F_(yy)^ ("")\දකුණ)$$

දෙවන සාධකය (වරහන් තුළ පිහිටා ඇත) මෙම ආකෘතියෙන් නිරූපණය කළ හැක:

$\වමේ| \begin(array) (cc) F_(xx)^("") & F_(xy)^("") \\ F_(xy)^("") & F_(yy)^("") \end (අරාව) \right|$ එනම් Lagrange ශ්‍රිතයේ Hessian වේ. $H > 0$ නම් $d^2F< 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F >$0, i.e. අපට $z=f(x,y)$ ශ්‍රිතයේ කොන්දේසි සහිත අවමයක් ඇත.

$H$ නිර්ණායකයේ ආකෘතිය මත සටහන් කරන්න. පෙන්වන්න / සඟවන්න

$$ H=-\left|\begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_ (xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \ අවසානය(අරාව) \right| $$

මෙම තත්වය තුළ, ඉහත සකසන ලද රීතිය පහත පරිදි වෙනස් වේ: $H > 0$ නම්, ශ්‍රිතයට කොන්දේසි සහිත අවම අගයක් සහ $H සඳහා< 0$ получим условный максимум функции $z=f(x,y)$. При решении задач следует учитывать такие нюансы.

කොන්දේසි සහිත අන්තයක් සඳහා විචල්‍ය දෙකක ශ්‍රිතයක් අධ්‍යයනය කිරීම සඳහා ඇල්ගොරිතම

1. Lagrange ශ්‍රිතය රචනා කරන්න $F(x,y)=f(x,y)+\lambda\varphi(x,y)$
2. පද්ධතිය විසඳන්න $ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \ varphi(x,y)=0.\end(aligned)\right.$
3. පෙර ඡේදයේ ඇති එක් එක් ස්ථාවර ලක්ෂ්‍යවල අන්තයේ ස්වභාවය තීරණය කරන්න. මෙය සිදු කිරීම සඳහා, පහත සඳහන් ඕනෑම ක්රමයක් භාවිතා කරන්න:
   • $H$ නිර්ණය කරන්න සහ එහි ලකුණ සොයා ගන්න
   • සීමා සමීකරණය සැලකිල්ලට ගනිමින්, $d^2F$ ලකුණ ගණනය කරන්න

n විචල්‍යවල ශ්‍රිත සඳහා Lagrange ගුණ කිරීමේ ක්‍රමය

අපට $n$ විචල්‍ය $z=f(x_1,x_2,\ldots,x_n)$ සහ $m$ සීමා සමීකරණ ($n > m$) වල ශ්‍රිතයක් ඇතැයි සිතමු.

$$\varphi_1(x_1,x_2,\ldots,x_n)=0; \; \varphi_2(x_1,x_2,\ldots,x_n)=0,\ldots,\varphi_m(x_1,x_2,\ldots,x_n)=0.$$

Lagrange ගුණකය $\lambda_1,\lambda_2,\ldots,\lambda_m$ ලෙස සඳහන් කරමින්, අපි Lagrange ශ්‍රිතය සම්පාදනය කරමු:

$$F(x_1,x_2,\ldots,x_n,\lambda_1,\lambda_2,\ldots,\lambda_m)=f+\lambda_1\varphi_1+\lambda_2\varphi_2+\ldots+\lambda_m\varphi_m$$

කොන්දේසි සහිත අන්තයක් පැවතීම සඳහා අවශ්‍ය කොන්දේසි ලබා දී ඇත්තේ ස්ථිතික ලක්ෂ්‍යවල ඛණ්ඩාංක සහ ලැග්‍රේන්ජ් ගුණකවල අගයන් සොයා ගන්නා සමීකරණ පද්ධතියක් මගිනි:

$$\left\(\begin(aligned) & \frac(\partial F)(\partial x_i)=0; (i=\overline(1,n))\\ & \varphi_j=0; (j=\ overline(1,m)) \end(aligned) \right.$$

$d^2F$ ලකුණ භාවිතයෙන් පෙර පරිදිම ශ්‍රිතයක් සොයාගත් ස්ථානයේ කොන්දේසි සහිත අවමයක් හෝ කොන්දේසි සහිත උපරිමයක් තිබේද යන්න සොයා බැලිය හැකිය. සොයාගත් ලක්ෂ්‍යයේ $d^2F > 0$ නම්, ශ්‍රිතයට කොන්දේසි සහිත අවම අගයක් ඇත, නමුත් $d^2F නම්< 0$, - то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

න්‍යාස නිර්ණය $\left| \begin(array) (cccc) \frac(\partial^2F)(\partial x_(1)^(2)) & \frac(\partial^2F)(\partial x_(1)\partial x_(2) ) & \frac(\partial^2F)(\partial x_(1)\partial x_(3)) &\ldots & \frac(\partial^2F)(\partial x_(1)\partial x_(n)) \\ \frac(\partial^2F)(\partial x_(2)\partial x_1) & \frac(\partial^2F)(\partial x_(2)^(2)) & \frac(\partial^2F )(\partial x_(2)\partial x_(3)) &\ldots & \frac(\partial^2F)(\partial x_(2)\partial x_(n))\\ \frac(\partial^2F )(\partial x_(3) \partial x_(1)) & \frac(\partial^2F)(\partial x_(3)\partial x_(2)) & \frac(\partial^2F)(\partial x_(3)^(2)) &\ldots & \frac(\partial^2F)(\partial x_(3)\partial x_(n))\\ \ldots & \ldots & \ldots &\ldots & \ ldots\\ \frac(\partial^2F)(\partial x_(n)\partial x_(1)) & \frac(\partial^2F)(\partial x_(n)\partial x_(2)) & \ frac(\partial^2F)(\partial x_(n)\partial x_(3)) &\ldots & \frac(\partial^2F)(\partial x_(n)^(2))\\ \end( array) \right|$ $L$ matrix හි රතු පැහැයෙන් උද්දීපනය කර ඇත්තේ Lagrange ශ්‍රිතයේ Hessian වේ. අපි පහත රීතිය භාවිතා කරමු:

• කෙළවරේ බාල වයස්කරුවන්ගේ සලකුණු $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ න්‍යාස $L$ $(-1)^m$ ලකුණ සමඟ සමපාත වේ, එවිට අධ්‍යයනයට ලක්වන ස්ථාවර ලක්ෂ්‍යය $z ශ්‍රිතයේ කොන්දේසි සහිත අවම ලක්ෂ්‍යය වේ. =f(x_1,x_2 ,x_3,\ldots,x_n)$.
• කෙළවරේ බාල වයස්කරුවන්ගේ සලකුණු $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ විකල්ප, සහ සුළු $H_(2m+1)$ හි ලකුණ $(-1)^(m+1 අංකයේ ලකුණ සමග සමපාත වේ. )$, එවිට අධ්‍යයනය කරන ලද ස්ථාවර ලක්ෂ්‍යය $z=f(x_1,x_2,x_3,\ldots,x_n)$ ශ්‍රිතයේ කොන්දේසි සහිත උපරිම ලක්ෂ්‍යය වේ.

උදාහරණ #1

$x^2+y^2=10$ කොන්දේසිය යටතේ $z(x,y)=x+3y$ ශ්‍රිතයේ කොන්දේසිගත අන්තය සොයන්න.

මෙම ගැටලුවේ ජ්යාමිතික අර්ථ නිරූපණය පහත පරිදි වේ: එය විශාලතම සහ සොයා ගැනීමට අවශ්ය වේ කුඩාම අගයතලය $x^2+y^2=10$ සමඟ ඡේදනය වන ස්ථාන සඳහා $z=x+3y$ අදාළ වේ.

සීමා සමීකරණයෙන් එක් විචල්‍යයක් තවත් විචල්‍යයක් අනුව ප්‍රකාශ කිරීම තරමක් අපහසු වන අතර එය $z(x,y)=x+3y$ ශ්‍රිතයට ආදේශ කිරීම, එබැවින් අපි Lagrange ක්‍රමය භාවිතා කරමු.

$\varphi(x,y)=x^2+y^2-10$ සඳහන් කරමින්, අපි Lagrange ශ්‍රිතය සම්පාදනය කරමු:

$$ F(x,y)=z(x,y)+\lambda \varphi(x,y)=x+3y+\lambda(x^2+y^2-10);\\ \frac(\partial F)(\partial x)=1+2\lambda x; \frac(\partial F)(\partial y)=3+2\lambda y. $$

Lagrange ශ්‍රිතයේ ස්ථිතික ලක්ෂ්‍ය නිර්ණය කිරීම සඳහා සමීකරණ පද්ධතිය අපි ලියා තබමු:

$$ \left \( \begin(aligned) & 1+2\lambda x=0;\\ & 3+2\lambda y=0;\\ & x^2+y^2-10=0. \end (පෙළගැසී)\දකුණට.$$

අපි $\lambda=0$ උපකල්පනය කරන්නේ නම්, පළමු සමීකරණය වන්නේ: $1=0$. එහි ප්‍රතිඵලය වන ප්‍රතිවිරෝධය $\lambda\neq 0$ බව පවසයි. කොන්දේසිය යටතේ $\lambda\neq 0$, පළමු සහ දෙවන සමීකරණ වලින් අපට ඇත: $x=-\frac(1)(2\lambda)$, $y=-\frac(3)(2\lambda) $. ලබාගත් අගයන් තුන්වන සමීකරණයට ආදේශ කිරීමෙන් අපට ලැබෙන්නේ:

$$ \left(-\frac(1)(2\lambda) \right)^2+\left(-\frac(3)(2\lambda) \right)^2-10=0;\\ \frac (1)(4\lambda^2)+\frac(9)(4\lambda^2)=10; \lambda^2=\frac(1)(4); \left[ \begin(aligned) & \lambda_1=-\frac(1)(2);\\ & \lambda_2=\frac(1)(2). \end(පෙළගැසී) \දකුණට.\\ \begin(aligned) & \lambda_1=-\frac(1)(2); \; x_1=-\frac(1)(2\lambda_1)=1; \; y_1=-\frac(3)(2\lambda_1)=3;\\ & \lambda_2=\frac(1)(2); \; x_2=-\frac(1)(2\lambda_2)=-1; \; y_2=-\frac(3)(2\lambda_2)=-3.\end(පෙළගැසී) $$

එබැවින්, පද්ධතියට විසඳුම් දෙකක් ඇත: $x_1=1;\; y_1=3;\; \lambda_1=-\frac(1)(2)$ සහ $x_2=-1;\; y_2=-3;\; \lambda_2=\frac(1)(2)$. අපි එක් එක් නිශ්චල ලක්ෂ්‍යයේ අන්තයේ ස්වභාවය සොයා බලමු: $M_1(1;3)$ සහ $M_2(-1;-3)$. මෙය සිදු කිරීම සඳහා, අපි එක් එක් ලක්ෂ්යයේ නිර්ණායක $H$ ගණනය කරමු.

$$ \varphi_(x)^(")=2x;\; \varphi_(y)^(")=2y;\; F_(xx)^("")=2\lambda;\; F_(xy)^("")=0;\; F_(yy)^("")=2\lambda.\\ H=\left| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \left| \begin(array) (ccc) 0 & 2x & 2y\\ 2x & 2\lambda & 0 \\ 2y & 0 & 2\lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right| $$

$M_1(1;3)$ යන ලක්ෂ්‍යයේදී අපට ලැබෙන්නේ: $H=8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & 1 & 3\\ 1 & -1/2 & 0 \\ 3 & 0 & -1/2 \end(array) \right|=40 > 0$, එසේ ලක්ෂ්‍යයේදී $M_1(1;3)$ ශ්‍රිතයට $z(x,y)=x+3y$ කොන්දේසි සහිත උපරිමයක් ඇත, $z_(\max)=z(1;3)=10$.

ඒ හා සමානව, $M_2(-1;-3)$ යන ලක්ෂ්‍යයේදී අපට හමුවන්නේ: $H=8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end(array) \right|=-40$. $H සිට< 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{\min}=z(-1;-3)=-10$.

එක් එක් ලක්ෂ්‍යයේ $H$ නිර්ණායකයේ අගය ගණනය කරනවා වෙනුවට, එය පුළුල් කිරීම වඩාත් පහසු බව මම සටහන් කරමි. සාමාන්ය දැක්ම. විස්තර සහිත පෙළ අවුල් නොකිරීමට, මම මෙම ක්‍රමය සටහනක් යටතේ සඟවන්නෙමි.

සාමාන්‍ය ආකාරයෙන් නිර්ණායක $H$ අංකනය. පෙන්වන්න / සඟවන්න

$$ H=8\cdot\left|\begin(array)(ccc)0&x&y\\x&\lambda&0\\y&0&\lambda\end(array)\right| =8\cdot\left(-\lambda(y^2)-\lambda(x^2)\right) =-8\lambda\cdot\left(y^2+x^2\දකුණ). $$

ප්‍රතිපත්තිමය වශයෙන්, $H$ සතුව ඇත්තේ කුමන ලකුණද යන්න දැනටමත් පැහැදිලිය. $M_1$ හෝ $M_2$ කිසිවක් මූලාරම්භය සමග සමපාත නොවන බැවින්, $y^2+x^2>0$. එබැවින්, $H$ හි ලකුණ $\lambda$ ලකුණට විරුද්ධ වේ. ඔබට ගණනය කිරීම් ද සම්පූර්ණ කළ හැකිය:

$$ \begin(aligned) &H(M_1)=-8\cdot\left(-\frac(1)(2)\දකුණ)\cdot\left(3^2+1^2\දකුණ)=40;\ \ &H(M_2)=-8\cdot\frac(1)(2)\cdot\left((-3)^2+(-1)^2\right)=-40. \අවසන් (පෙළගැසී) $$

$M_1(1;3)$ සහ $M_2(-1;-3)$ යන ස්ථාවර ලක්ෂ්‍යවල අන්තයේ ස්වභාවය පිළිබඳ ප්‍රශ්නය $H$ නිර්ණය කිරීමකින් තොරව විසඳිය හැක. එක් එක් ස්ථාවර ලක්ෂ්‍යයේ $d^2F$ ලකුණ සොයන්න:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=2\lambda \left( dx^2+dy^2\දකුණ) $$

$dx^2$ යන අංකනයෙන් අදහස් කරන්නේ හරියටම $dx$ දෙවන බලයට නංවා ඇති බව මම සටහන් කරමි, i.e. $\වම(dx\දකුණ)^2$. එබැවින් අපට ඇත්තේ: $dx^2+dy^2>0$, එබැවින් $\lambda_1=-\frac(1)(2)$ සඳහා අපට $d^2F ලැබේ< 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

පිළිතුර: $(-1;-3)$ ලක්ෂ්‍යයේ දී ශ්‍රිතයට කොන්දේසි සහිත අවම අගයක් ඇත, $z_(\min)=-10$. $(1;3)$ ලක්ෂ්‍යයේදී ශ්‍රිතයට කොන්දේසි සහිත උපරිමයක් ඇත, $z_(\max)=10$

උදාහරණ #2

$x+y=0$ කොන්දේසිය යටතේ $z(x,y)=3y^3+4x^2-xy$ ශ්‍රිතයේ කොන්දේසිගත අන්තය සොයන්න.

පළමු මාර්ගය (Lagrange ගුණක ක්රමය)

$\varphi(x,y)=x+y$ සඳහන් කරමින් අපි Lagrange ශ්‍රිතය සම්පාදනය කරමු: $F(x,y)=z(x,y)+\lambda \varphi(x,y)=3y^3+4x ^2 -xy+\lambda(x+y)$.

$$ \frac(\partial F)(\partial x)=8x-y+\lambda; \; \frac(\partial F)(\partial y)=9y^2-x+\lambda.\\ \left \( \begin(aligned) & 8x-y+\lambda=0;\\ & 9y^2-x+\ lambda=0;\\&x+y=0.\end(aligned)\right.$$

පද්ධතිය විසඳීමෙන්, අපට ලැබෙන්නේ: $x_1=0$, $y_1=0$, $\lambda_1=0$ සහ $x_2=\frac(10)(9)$, $y_2=-\frac(10)(9 )$ , $\lambda_2=-10$. අපට ස්ථාවර ලක්ෂ්‍ය දෙකක් තිබේ: $M_1(0;0)$ සහ $M_2 \left(\frac(10)(9);-\frac(10)(9) \දකුණ)$. අපි $H$ නිර්ණායකය භාවිතයෙන් එක් එක් නිශ්චල ලක්ෂ්‍යයේ අන්තයේ ස්වභාවය සොයා ගනිමු.

$$ H=\වම| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \left| \begin(array) (ccc) 0 & 1 & 1\\ 1 & 8 & -1 \\ 1 & -1 & 18y \end(array) \right|=-10-18y $$

ලක්ෂ්‍යයේ $M_1(0;0)$ $H=-10-18\cdot 0=-10< 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{\min}=0$. В точке $M_2\left(\frac{10}{9};-\frac{10}{9}\right)$ $H=10 >0$, එබැවින් මෙම අවස්ථාවේදී ශ්‍රිතයට කොන්දේසි සහිත උපරිමයක් ඇත, $z_(\max)=\frac(500)(243)$.

අපි $d^2F$ ලකුණ මත පදනම්ව, වෙනස් ක්‍රමයක් මගින් එක් එක් ලක්ෂ්‍යයේ අන්තයේ ස්වභාවය විමර්ශනය කරමු:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=8dx^2-2dxdy+ 18ydy ^2 $$

$x+y=0$ යන සීමා සමීකරණයෙන් අපට ඇත්තේ: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

$$ d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2 $$

$ d^2F \Bigr|_(M_1)=10 dx^2 > 0$ නිසා, $M_1(0;0)$ යනු $z(x,y)=3y^3+ ශ්‍රිතයේ කොන්දේසි සහිත අවම ලක්ෂ්‍යය වේ. 4x^ 2-xy$. එලෙසම, $d^2F \Bigr|_(M_2)=-10 dx^2< 0$, т.е. $M_2\left(\frac{10}{9}; -\frac{10}{9} \right)$ - точка условного максимума.

දෙවන මාර්ගය

$x+y=0$ සීමා සමීකරණයෙන් අපට ලැබෙන්නේ: $y=-x$. $z(x,y)=3y^3+4x^2-xy$ ශ්‍රිතය වෙත $y=-x$ ආදේශ කිරීම, අපි $x$ විචල්‍යයේ යම් ශ්‍රිතයක් ලබා ගනිමු. අපි මෙම ශ්‍රිතය $u(x)$ ලෙස දක්වමු:

$$ u(x)=z(x,-x)=3\cdot(-x)^3+4x^2-x\cdot(-x)=-3x^3+5x^2. $$

මේ අනුව, අපි විචල්‍ය දෙකක ශ්‍රිතයක කොන්දේසි සහිත අන්තය සොයා ගැනීමේ ගැටලුව එක් විචල්‍යයක ශ්‍රිතයක අන්තය තීරණය කිරීමේ ගැටලුව දක්වා අඩු කළෙමු.

$$ u_(x)^(")=-9x^2+10x;\\ -9x^2+10x=0; \; x\cdot(-9x+10)=0;\\ x_1=0; \ ;y_1=-x_1=0;\\ x_2=\frac(10)(9);\;y_2=-x_2=-\frac(10)(9).$$

ලකුණු ලබා ගත්තා $M_1(0;0)$ සහ $M_2\left(\frac(10)(9); -\frac(10)(9)\දකුණ)$. වැඩිදුර පර්යේෂණ පාඨමාලාවෙන් දනී අවකල ගණනයඑක් විචල්‍යයක ශ්‍රිත. එක් එක් නිශ්චල ලක්ෂ්‍යයේ $u_(xx)^("")$ හි ලකුණ පරීක්ෂා කිරීමෙන් හෝ සොයාගත් ලක්ෂ්‍යවල $u_(x)^(")$ හි ලකුණ වෙනස් වීම පරීක්ෂා කිරීමෙන්, අපි පළමු විසඳුමේ ඇති නිගමනම ලබා ගනිමු. උදාහරණයක් ලෙස, පිරික්සුම් ලකුණ $u_(xx)^("")$:

$$u_(xx)^("")=-18x+10;\\ u_(xx)^("")(M_1)=10;\;u_(xx)^("")(M_2)=- 10.$$

$u_(xx)^("")(M_1)>0$ නිසා, $M_1$ යනු $u(x)$ ශ්‍රිතයේ අවම ලක්ෂ්‍යය වන අතර $u_(\min)=u(0)=0 $ $u_(xx)^("")(M_2) සිට<0$, то $M_2$ - точка максимума функции $u(x)$, причём $u_{\max}=u\left(\frac{10}{9}\right)=\frac{500}{243}$.

ලබා දී ඇති සම්බන්ධතා තත්ත්වය යටතේ $u(x)$ ශ්‍රිතයේ අගයන් $z(x,y)$ ශ්‍රිතයේ අගයන් සමග සමපාත වේ, i.e. $u(x)$ ශ්‍රිතයේ සොයාගත් අන්තය $z(x,y)$ ශ්‍රිතයේ අපේක්ෂිත කොන්දේසිගත අන්තයයි.

පිළිතුර: $(0;0)$ ලක්ෂ්‍යයේදී ශ්‍රිතයට කොන්දේසි සහිත අවම අගයක් ඇත, $z_(\min)=0$. ලක්ෂ්‍යයේ $\left(\frac(10)(9); -\frac(10)(9) \දකුණ)$ ශ්‍රිතයට කොන්දේසි සහිත උපරිමයක් ඇත, $z_(\max)=\frac(500)(243 )$.

අපි තවත් එක් උදාහරණයක් සලකා බලමු, $d^2F$ හි ලකුණ නිර්ණය කිරීමෙන් අපි අන්තයේ ස්වභාවය සොයා ගනිමු.

උදාහරණ #3

$x$ සහ $y$ යන විචල්‍ය ධන නම් සහ $\frac(x^2)(8)+\frac( සීමා සමීකරණය තෘප්තිමත් කරයි නම් $z=5xy-4$ ශ්‍රිතයේ උපරිම සහ අවම අගයන් සොයන්න. y^2)(2) -1=0$.

Lagrange ශ්‍රිතය සම්පාදනය කරන්න: $F=5xy-4+\lambda \left(\frac(x^2)(8)+\frac(y^2)(2)-1 \දකුණ)$. Lagrange ශ්‍රිතයේ නිශ්චල ලක්ෂ්‍ය සොයන්න:

$$ F_(x)^(")=5y+\frac(\lambda x)(4); \; F_(y)^(")=5x+\lambda y.\\ \වම \( \ආරම්භ(පෙළගැසී) & 5y+\frac(\lambda x)(4)=0;\\ & 5x+\lambda y=0;\\ & \frac(x^2)(8)+\frac(y^2)(2)- 1=0;\\ & x > 0; \; y > 0. \අවසන්(පෙළගැසී) \දකුණට.$$

සියලු වැඩිදුර පරිවර්තනයන් $x > 0 සැලකිල්ලට ගනිමින් සිදු කරනු ලැබේ; \; y > 0$ (මෙය ගැටලුවේ තත්ත්වය තුළ නියම කර ඇත). දෙවන සමීකරණයෙන්, අපි $\lambda=-\frac(5x)(y)$ ප්‍රකාශ කර සොයාගත් අගය පළමු සමීකරණයට ආදේශ කරමු: $5y-\frac(5x)(y)\cdot \frac(x)( 4)=0$ , $4y^2-x^2=0$, $x=2y$. තුන්වන සමීකරණයට $x=2y$ ආදේශ කිරීමෙන්, අපට ලැබෙන්නේ: $\frac(4y^2)(8)+\frac(y^2)(2)-1=0$, $y^2=1$, $y =1$.

$y=1$ සිට, පසුව $x=2$, $\lambda=-10$. $(2;1)$ ලක්ෂ්‍යයේ අන්තයේ ස්වභාවය තීරණය වන්නේ $d^2F$ ලකුණෙනි.

$$ F_(xx)^("")=\frac(\lambda)(4); \; F_(xy)^("")=5; \; F_(yy)^("")=\lambda. $$

$\frac(x^2)(8)+\frac(y^2)(2)-1=0$ සිට, එවිට:

$$ d\left(\frac(x^2)(8)+\frac(y^2)(2)-1\දකුණ)=0; \; d\left(\frac(x^2)(8) \දකුණ)+d\වම(\frac(y^2)(2) \දකුණ)=0; \; \frac(x)(4)dx+ydy=0; \; dy=-\frac(xdx)(4y). $$

ප්‍රතිපත්තිමය වශයෙන්, මෙහිදී ඔබට $x=2$, $y=1$ යන ස්ථාවර ලක්ෂ්‍යයේ ඛණ්ඩාංක සහ $\lambda=-10$ යන පරාමිතියෙහි ඛණ්ඩාංක වහාම ආදේශ කළ හැක.

$$ F_(xx)^("")=\frac(-5)(2); \; F_(xy)^("")=-10; \; dy=-\frac(dx)(2).\\ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^(" ")dy^2=-\frac(5)(2)dx^2+10dx\cdot \left(-\frac(dx)(2) \right)-10\cdot \left(-\frac(dx) (2) \right)^2=\\ =-\frac(5)(2)dx^2-5dx^2-\frac(5)(2)dx^2=-10dx^2. $$

කෙසේ වෙතත්, කොන්දේසි සහිත අන්තයක් සඳහා වෙනත් ගැටළු වලදී, ස්ථාවර කරුණු කිහිපයක් තිබිය හැකිය. එවැනි අවස්ථාවන්හිදී, $d^2F$ සාමාන්‍ය ආකෘතියකින් නිරූපණය කිරීම වඩා හොඳය, ඉන්පසු ලැබෙන එක් එක් ස්ථාවර ලක්ෂ්‍යවල ඛණ්ඩාංක ප්‍රතිඵල ප්‍රකාශනයට ආදේශ කරන්න:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=\frac(\lambda) (4)dx^2+10\cdot dx\cdot \frac(-xdx)(4y) +\lambda\cdot \left(-\frac(xdx)(4y) \දකුණ)^2=\\ =\frac (\lambda)(4)dx^2-\frac(5x)(2y)dx^2+\lambda \cdot \frac(x^2dx^2)(16y^2)=\වම(\frac(\lambda) )(4)-\frac(5x)(2y)+\frac(\lambda \cdot x^2)(16y^2) \දකුණ)\cdot dx^2 $$

$x=2$, $y=1$, $\lambda=-10$ ආදේශ කිරීම, අපට ලැබෙන්නේ:

$$ d^2 F=\left(\frac(-10)(4)-\frac(10)(2)-\frac(10 \cdot 4)(16) \දකුණ)\cdot dx^2=- 10dx^2. $$

$d^2F=-10\cdot dx^2 සිට< 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{\max}=10-4=6$.

පිළිතුර: $(2;1)$ ලක්ෂ්‍යයේදී ශ්‍රිතයට කොන්දේසි සහිත උපරිමයක් ඇත, $z_(\max)=6$.

මීළඟ කොටසින්, අපි විචල්‍ය විශාල සංඛ්‍යාවක ශ්‍රිත සඳහා Lagrange ක්‍රමය යෙදීම සලකා බලමු.

උදාහරණයක්

එය සපයා ඇති ශ්‍රිතයේ අන්තය සොයන්න xහා හිදීඅනුපාතය මගින් සම්බන්ධ වේ: . ජ්‍යාමිතික වශයෙන්, ගැටලුව යන්නෙන් අදහස් කරන්නේ පහත සඳහන් දේ: ඉලිප්සයක් මත
ගුවන් යානය
.

මෙම ගැටළුව පහත පරිදි විසඳිය හැකිය: සමීකරණයෙන්
සොයාගන්න
x:

බව සපයා ඇත
, එක් විචල්‍යයක ශ්‍රිතයක අන්තය සොයා ගැනීමේ ගැටලුව දක්වා අඩු කර ඇත, පරතරය මත
.

ජ්‍යාමිතික වශයෙන්, ගැටලුව යන්නෙන් අදහස් කරන්නේ පහත සඳහන් දේ: ඉලිප්සයක් මත සිලින්ඩරය හරස් කිරීමෙන් ලබා ගනී
ගුවන් යානය
, අයදුම්කරුගේ උපරිම හෝ අවම අගය සොයා ගැනීමට අවශ්‍ය වේ (රූපය 9). මෙම ගැටළුව පහත පරිදි විසඳිය හැකිය: සමීකරණයෙන්
සොයාගන්න
. y හි සොයාගත් අගය තලයේ සමීකරණයට ආදේශ කිරීමෙන්, අපි එක් විචල්‍යයක ශ්‍රිතයක් ලබා ගනිමු. x:

මේ අනුව, ශ්රිතයේ අන්තය සොයා ගැනීමේ ගැටළුව
බව සපයා ඇත
, කොටසක එක් විචල්‍යයක ශ්‍රිතයක අන්තය සොයා ගැනීමේ ගැටලුව දක්වා අඩු කර ඇත.

ඒ නිසා, කොන්දේසි සහිත අන්තයක් සොයා ගැනීමේ ගැටලුවවෛෂයික ශ්‍රිතයේ අන්තය සොයා ගැනීමේ ගැටලුවයි
, විචල්‍ය බව සපයා ඇත xහා හිදීසීමාවට යටත්ව
කියලා සම්බන්ධතා සමීකරණය.

අපි එහෙම කියන්නම් තිත
, සීමා සමීකරණය තෘප්තිමත් කිරීම, දේශීය කොන්දේසි සහිත උපරිම ලක්ෂ්‍යයකි (අවම) අසල්වැසි ප්රදේශයක් තිබේ නම්
ඕනෑම ලකුණු සඳහා එවැනි
, එහි ඛණ්ඩාංක බාධක සමීකරණය තෘප්තිමත් කරයි, අසමානතාවය රඳවා ගනී.

සන්නිවේදනයේ සමීකරණයෙන් එය සඳහා ප්රකාශනයක් සොයා ගත හැකි නම් හිදී, පසුව, මෙම ප්‍රකාශනය මුල් ශ්‍රිතයට ආදේශ කරමින්, අපි දෙවැන්න එක් විචල්‍යයක සංකීර්ණ ශ්‍රිතයක් බවට පත් කරමු. X.

කොන්දේසි සහිත අන්ත ගැටලුව විසඳීම සඳහා පොදු ක්රමය වේ Lagrange ගුණ කිරීමේ ක්රමය. අපි සහායක ශ්‍රිතයක් නිර්මාණය කරමු, එහිදී ─ යම් අංකයක්. මෙම කාර්යය ලෙස හැඳින්වේ Lagrange කාර්යය, ඒ ─ Lagrange ගුණකය. මේ අනුව, කොන්දේසි සහිත අන්තයක් සොයා ගැනීමේ ගැටලුව Lagrange ශ්‍රිතය සඳහා දේශීය අන්ත ලක්ෂ්‍ය සොයා ගැනීම දක්වා අඩු කර ඇත. හැකි අන්තයක ලක්ෂ්‍ය සොයා ගැනීම සඳහා, නොදන්නා කරුණු තුනක් සමඟ සමීකරණ 3 ක පද්ධතියක් විසඳීම අවශ්‍ය වේ. x, yහා.

එවිට පහත සඳහන් ප්‍රමාණවත් අන්ත තත්ත්වය භාවිතා කළ යුතුය.

සිද්ධාන්තය. ලක්ෂ්‍යය Lagrange ශ්‍රිතය සඳහා විය හැකි අන්තයේ ලක්ෂ්‍යයක් වේවා. ලක්ෂ්‍යය ආසන්නයේ යැයි අපි උපකල්පනය කරමු
ශ්‍රිතවල අඛණ්ඩ දෙවන අනුපිළිවෙලෙහි අර්ධ ව්‍යුත්පන්න පවතී හා . දක්වන්න

එවිට නම්
, එවිට
─ ශ්‍රිතයේ කොන්දේසි සහිත අන්ත ලක්ෂ්‍යය
සීමා සමීකරණයේදී
මේ අතර, නම්
, එවිට
─ කොන්දේසි සහිත අවම ලක්ෂ්‍යය, නම්
, එවිට
─ කොන්දේසි සහිත උපරිම ලක්ෂ්යය.

§අට. අනුක්‍රමණය සහ දිශානුගත ව්‍යුත්පන්නය

කාර්යයට ඉඩ දෙන්න
සමහර (විවෘත) වසම තුළ අර්ථ දක්වා ඇත. ඕනෑම කරුණක් සලකා බලන්න
මෙම ප්රදේශය සහ ඕනෑම සෘජු රේඛාවක් (අක්ෂයක්) මෙම ලක්ෂ්යය හරහා ගමන් කිරීම (රූපය 1). ඉඩ
- මෙම අක්ෂයේ වෙනත් ලක්ෂයක්,
- අතර කොටසෙහි දිග
හා
, දිශානතිය නම් ප්ලස් ලකුණක් සමඟ ගෙන ඇත
අක්ෂයේ දිශාව සමග සමපාත වේ , සහ ඒවායේ දිශාවන් විරුද්ධ නම් අඩු ලකුණක් සමඟ.

ඉඩ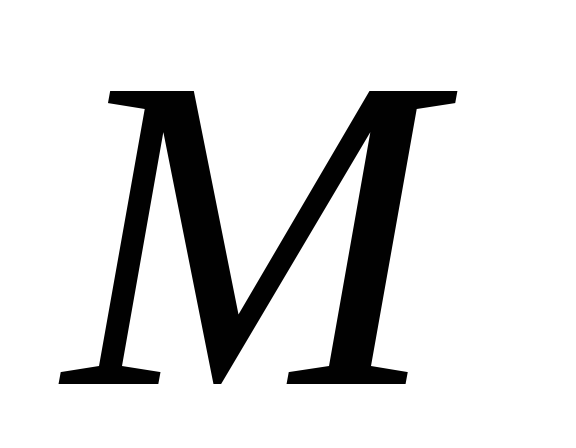
දින නියමයක් නොමැතිව ළඟා වේ
. සීමාව

කියලා ශ්රිත ව්යුත්පන්නය
දෙසට (හෝ අක්ෂය දිගේ ) සහ පහත පරිදි දැක්වේ:

.

මෙම ව්‍යුත්පන්නය ලක්ෂ්‍යයේ ශ්‍රිතයේ "වෙනස් වීමේ අනුපාතය" සංලක්ෂිත කරයි
දෙසට . විශේෂයෙන්ම, සහ සාමාන්ය අර්ධ ව්යුත්පන්න ,"දිශාව සම්බන්ධයෙන්" ව්‍යුත්පන්න ලෙසද සිතිය හැක.

දැන් එම ශ්‍රිතය යැයි සිතමු
සලකා බලනු ලබන කලාපයේ අඛණ්ඩ අර්ධ ව්‍යුත්පන්නයන් ඇත. අක්ෂය ඉඩ දෙන්න ඛණ්ඩාංක අක්ෂ සමඟ කෝණ සාදයි
හා . කරන ලද උපකල්පන යටතේ, දිශානුගත ව්යුත්පන්නය පවතින අතර සූත්‍රයෙන් ප්‍රකාශ වේ

.

දෛශිකය නම්
එහි ඛණ්ඩාංක මගින් සකසා ඇත
, පසුව ශ්රිතයේ ව්යුත්පන්නය
දෛශිකයේ දිශාවට
සූත්රය භාවිතයෙන් ගණනය කළ හැක:

.

ඛණ්ඩාංක සහිත දෛශිකය
කියලා අනුක්‍රමණ දෛශිකයකාර්යයන්
ලක්ෂ්යයේ
. ශ්‍රේණියේ දෛශිකය යම් ලක්ෂ්‍යයක ශ්‍රිතයේ වේගවත්ම වැඩිවීමේ දිශාව පෙන්නුම් කරයි.

උදාහරණයක්

ශ්‍රිතයක් , ලක්ෂ්‍යයක් A(1, 1) සහ දෛශිකයක් ලබා දී ඇත
. සොයන්න: 1) A ලක්ෂ්‍යයේ grad z; 2) දෛශිකයේ දිශාවට A ලක්ෂ්‍යයේ ව්‍යුත්පන්නය .

ලක්ෂ්‍යයක දී ඇති ශ්‍රිතයක අර්ධ ව්‍යුත්පන්න
:

;
.

එවිට මෙම ලක්ෂ්‍යයේ ශ්‍රිතයේ අනුක්‍රමණ දෛශිකය වන්නේ:
. අනුක්‍රමණ දෛශිකය දෛශික ප්‍රසාරණයක් භාවිතයෙන් ද ලිවිය හැක හා :

. කාර්යය ව්යුත්පන්නය දෛශිකයේ දිශාවට :

ඒ නිසා,
,
.◄