0 සිට 360 දක්වා වූ ත්‍රිකෝණමිතික ශ්‍රිත වගුව. Sine, cosine, tangent සහ cotangent - OGE සහ USE හි ඔබ දැනගත යුතු සියල්ල

අපි ත්‍රිකෝණමිතිය පිළිබඳ අපගේ අධ්‍යයනය ආරම්භ කරමු සෘජු ත්රිකෝණය. සයින් සහ කෝසයින් යනු කුමක්ද යන්න මෙන්ම තියුණු කෝණයක ස්පර්ශක සහ කෝටැන්ජන්ට් මොනවාද යන්න නිර්වචනය කරමු. මේවා ත්‍රිකෝණමිතියේ මූලික කරුණු වේ.

ඒක මතක් කරන්න සෘජු කෝණයඅංශක 90 ට සමාන කෝණයකි. වෙනත් වචන වලින් කිවහොත්, දිග හැරුණු කොනෙන් අඩක්.

තියුණු කෙළවර- අංශක 90 ට අඩු.

Obtuse කෝණය- අංශක 90 ට වැඩි. එවැනි කෝණයක් සම්බන්ධයෙන්, "මොට" යනු අපහාසයක් නොව, ගණිතමය යෙදුමකි :-)

අපි සෘජුකෝණාස්රාකාර ත්රිකෝණයක් අඳින්නෙමු. සෘජු කෝණයක් සාමාන්යයෙන් දැක්වේ. කෙළවරට විරුද්ධ පැත්ත එකම අකුරකින් දක්වා ඇති බව සලකන්න, කුඩා පමණි. එබැවින්, A කෝණයට ප්‍රතිවිරුද්ධ පැත්ත සඳහන් වේ.

කෝණයක් අනුරූප ග්රීක අකුරින් දැක්වේ.

හයිපොටෙනස්සෘජුකෝණාස්‍ර ත්‍රිකෝණයක් යනු සෘජු කෝණයට විරුද්ධ පැත්තයි.

කකුල්- තියුණු කොන් වලට විරුද්ධ පැති.

කෙළවරට විරුද්ධ පාදය ලෙස හැඳින්වේ ප්රතිවිරුද්ධ(කෝණයට සාපේක්ෂව). කෙළවරේ එක් පැත්තක පිහිටා ඇති අනෙක් කකුල හැඳින්වේ යාබද.

සයිනස්සෘජුකෝණාශ්‍රය ත්‍රිකෝණයක තියුණු කෝණය යනු ප්‍රතිවිරුද්ධ පාදයේ කර්ණයට අනුපාතයයි:

කොසයින්සෘජුකෝණාස්රාකාර ත්රිකෝණයක තියුණු කෝණය - යාබද පාදයේ කර්ණයට අනුපාතය:

ස්පර්ශකසෘජුකෝණාස්රාකාර ත්රිකෝණයක තියුණු කෝණය - ප්රතිවිරුද්ධ පාදයේ අනුපාතය යාබදව:

තවත් (සමාන) අර්ථ දැක්වීමක්: උග්‍ර කෝණයක ස්පර්ශකය යනු කෝණයක සයින් එහි කෝසයිනයට අනුපාතයයි:

කෝටැන්ජන්ට්සෘජුකෝණාශ්‍රය ත්‍රිකෝණයක තියුණු කෝණය - යාබද පාදයේ ප්‍රතිවිරුද්ධයට අනුපාතය (හෝ, ඊට සමානව, කොසයින් සහ සයින් අනුපාතය):

පහත දක්වා ඇති සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් සඳහා මූලික අනුපාත කෙරෙහි අවධානය යොමු කරන්න. ගැටළු විසඳීමේදී ඔවුන් අපට ප්රයෝජනවත් වනු ඇත.

අපි ඒවායින් සමහරක් ඔප්පු කරමු.

හරි, අපි අර්ථ දැක්වීම් සහ ලිඛිත සූත්‍ර ලබා දී ඇත. නමුත් අපට sine, cosine, tangent සහ cotangent අවශ්‍ය වන්නේ ඇයි?

බව අපි දන්නා ඕනෑම ත්‍රිකෝණයක කෝණවල එකතුව වේ.

අතර සම්බන්ධය අපි දන්නවා පාර්ශවයන්සෘජු ත්රිකෝණය. මෙය පයිතගරස් ප්‍රමේය:.

ත්රිකෝණයක කෝණ දෙකක් දැන ගැනීමෙන් ඔබට තුන්වන එක සොයාගත හැකි බව පෙනේ. සෘජුකෝණාස්රාකාර ත්රිකෝණයක පැති දෙකක් දැන ගැනීමෙන් ඔබට තුන්වැන්න සොයාගත හැකිය. එබැවින්, කෝණ සඳහා - ඔවුන්ගේ අනුපාතය, පැති සඳහා - ඔවුන්ගේම. නමුත් සෘජුකෝණාස්රාකාර ත්රිකෝණයක එක් කෝණයක් (දකුණු පස හැර) සහ එක් පැත්තක් දන්නා නමුත් ඔබට අනෙක් පැති සොයා ගැනීමට අවශ්ය නම් කුමක් කළ යුතුද?

ප්‍රදේශයේ සහ තරු පිරුණු අහසේ සිතියම් සකස් කරමින් අතීතයේ මිනිසුන් මුහුණ දුන්නේ මෙයයි. සියල්ලට පසු, ත්රිකෝණයක සියලුම පැති සෘජුවම මැනීම සැමවිටම කළ නොහැකිය.

සයින්, කෝසයින් සහ ස්පර්ශක - ඒවා ද හැඳින්වේ කෝණයෙහි ත්රිකෝණමිතික ශ්රිත- අතර අනුපාතය දෙන්න පාර්ශවයන්හා කොන්ත්රිකෝණය. කෝණය දැන ගැනීමෙන්, ඔබට විශේෂ වගු භාවිතයෙන් එහි සියලුම ත්රිකෝණමිතික ශ්රිතයන් සොයාගත හැකිය. ත්‍රිකෝණයක සහ එහි එක් පැත්තක කෝණවල සයින, කෝසයින සහ ස්පර්ශක දැන ගැනීමෙන් ඔබට ඉතිරිය සොයාගත හැකිය.

අපි "හොඳ" කෝණ සඳහා සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් අගයන් වගුවක් ද අඳින්නෙමු.

මේසයේ ඇති රතු ඉරි දෙක සැලකිල්ලට ගන්න. කෝණවල අනුරූප අගයන් සඳහා, ස්පර්ශක සහ කෝටැන්ජන්ට් නොපවතී.

FIPI කාර්යයන් බැංකුවෙන් ත්‍රිකෝණමිතියේ ගැටලු කිහිපයක් විශ්ලේෂණය කරමු.

1. ත්‍රිකෝණයක කෝණය , . සොයන්න .

තත්පර හතරකින් ගැටලුව විසඳනු ලැබේ.

මන්ද , .

2. ත්‍රිකෝණයක කෝණය , , . සොයන්න .

පයිතගරස් ප්‍රමේයය මගින් සොයා ගනිමු.

ගැටලුව විසඳා ඇත.

බොහෝ විට ගැටළු වලදී කෝණ සහිත ත්රිකෝණ සහ හෝ කෝණ සහිත සහ . ඔවුන් සඳහා මූලික අනුපාත හදවතින් මතක තබා ගන්න!

කෝණ සහිත ත්රිකෝණයක් සඳහා සහ කෝණයට විරුද්ධ පාදය සමාන වේ උපකල්පිතයෙන් අඩක්.

කෝණ සහිත ත්‍රිකෝණයක් වන අතර එය සමද්වීපක වේ. එහි කර්ණය කකුලට වඩා ගුණයකින් විශාල වේ.

අපි සෘජුකෝණාස්රාකාර ත්රිකෝණ විසඳීම සඳහා ගැටළු සලකා බැලුවෙමු - එනම්, නොදන්නා පැති හෝ කෝණ සොයා ගැනීම සඳහා. නමුත් එය පමණක් නොවේ! හිදී විකල්ප භාවිතා කරන්නගණිතයේ දී, ත්‍රිකෝණයේ බාහිර කෝණයේ සයින්, කෝසයින්, ස්පර්ශක හෝ කෝටැන්ජන්ට් දිස්වන ගැටළු රාශියක් ඇත. මේ ගැන වැඩි විස්තර ඊළඟ ලිපියෙන්.

සයින් (), කෝසයින් (), ස්පර්ශක (), කෝටැන්ජන්ට් () යන සංකල්ප කෝණය යන සංකල්පය සමඟ වෙන් කළ නොහැකි ලෙස බැඳී ඇත. මේවා ගැන හොඳ අවබෝධයක් ලබා ගැනීමට, බැලූ බැල්මට සංකීර්ණ සංකල්ප (බොහෝ පාසල් සිසුන් තුළ භීතියක් ඇති කරයි) සහ "යකා තීන්ත ආලේප කර ඇති තරම් බියජනක නොවන" බවට වග බලා ගන්න, අපි මුල සිටම පටන් ගනිමු. සහ කෝණයක සංකල්පය තේරුම් ගන්න.

කෝණය පිළිබඳ සංකල්පය: රේඩියන්, උපාධිය

අපි පින්තූරය දෙස බලමු. දෛශිකය යම් ප්රමාණයකින් ලක්ෂ්යයට සාපේක්ෂව "හැරී". එබැවින් ආරම්භක ස්ථානයට සාපේක්ෂව මෙම භ්රමණයෙහි මිනුම වනු ඇත කෙළවරේ.

කෝණය පිළිබඳ සංකල්පය ගැන ඔබ දැනගත යුතු තවත් මොනවාද? හොඳයි, කෝණ ඒකක, ඇත්ත වශයෙන්ම!

ජ්‍යාමිතිය සහ ත්‍රිකෝණමිතිය යන දෙකෙහිම කෝණය අංශක සහ රේඩියන වලින් මැනිය හැක.

(අංශක) කෝණය රවුමේ කේන්ද්‍රීය කෝණය, රවුමේ කොටසට සමාන චක්‍ර චාපයක් මත පදනම් වේ. මේ අනුව, සම්පූර්ණ රවුම චක්රලේඛ චාප වල "කෑලි" වලින් සමන්විත වේ, නැතහොත් රවුම මගින් විස්තර කරන ලද කෝණය සමාන වේ.

එනම්, ඉහත රූපයේ දැක්වෙන්නේ සමාන කෝණයක්, එනම්, මෙම කෝණය පරිධියේ ප්රමාණයේ චක්රලේඛ චාපයක් මත පදනම් වේ.

රේඩියනවල කෝණයක් වෘත්තාකාර චාපයක් මත පදනම්ව රවුමක කේන්ද්‍රීය කෝණය ලෙස හැඳින්වේ, එහි දිග රවුමේ අරයට සමාන වේ. හොඳයි, ඔබට තේරුණාද? එසේ නොවේ නම්, අපි පින්තූරය දෙස බලමු.

ඉතින්, රූපය රේඩියනයකට සමාන කෝණයක් පෙන්වයි, එනම්, මෙම කෝණය රවුම් චාපයක් මත පදනම් වේ, එහි දිග රවුමේ අරයට සමාන වේ (දිග දිග හෝ අරයට සමාන වේ දිගට සමාන වේචාප). මේ අනුව, චාපයේ දිග සූත්රය මගින් ගණනය කරනු ලැබේ:

රේඩියනවල කේන්ද්‍රීය කෝණය කොහෙද.

හොඳයි, මෙය දැනගෙන, රවුමකින් විස්තර කරන ලද කෝණයක් රේඩියන කීයක් අඩංගු වේද යන්න ඔබට පිළිතුරු දිය හැකිද? ඔව්, මේ සඳහා ඔබ රවුමක පරිධිය සඳහා සූත්රය මතක තබා ගත යුතුය. එහි ඇය:

හොඳයි, දැන් අපි මෙම සූත්‍ර දෙක සහසම්බන්ධ කර රවුමෙන් විස්තර කර ඇති කෝණය සමාන බව ලබා ගනිමු. එනම්, අංශක සහ රේඩියනවල අගය සහසම්බන්ධ කිරීම, අපට එය ලැබේ. පිළිවෙලින්, . ඔබට පෙනෙන පරිදි, "අංශක" මෙන් නොව, "රේඩියන්" යන වචනය ඉවත් කර ඇත, මන්ද මිනුම් ඒකකය සාමාන්‍යයෙන් සන්දර්භයෙන් පැහැදිලි වේ.

රේඩියන කීයක් තිබේද? ඒක හරි!

තේරුම් ගත්තා ද? ඉන්පසු ඉදිරියට සවි කරන්න:

කිසියම් දුෂ්කරතාවයක් තිබේද? එහෙනම් බලන්න පිළිතුරු:

සෘජු ත්රිකෝණය: සයින්, කෝසයින්, ස්පර්ශක, කෝණයක කෝටැන්ජන්ට්

එබැවින්, කෝණය පිළිබඳ සංකල්පය හඳුනාගෙන ඇත. නමුත් කෝණයක සයින්, කෝසයින්, ස්පර්ශක, කෝටැන්ජන්ට් යනු කුමක්ද? අපි එය තේරුම් ගනිමු. මේ සඳහා සෘජුකෝණාස්රාකාර ත්රිකෝණයක් අපට උපකාර කරනු ඇත.

සෘජුකෝණාශ්‍රය ත්‍රිකෝණයක පැති හඳුන්වන්නේ කුමක්ද? එය හරි, කර්ණය සහ කකුල්: කර්ණය යනු සෘජු කෝණයට විරුද්ධ පැත්තේ පිහිටා ඇති පැත්තයි (අපගේ උදාහරණයේ, මෙය පැත්තයි); කකුල් යනු ඉතිරි පැති දෙකයි (ඒවාට යාබද සෘජු කෝණය), එපමනක් නොව, අපි කෝණයට සාපේක්ෂව කකුල් සලකන්නේ නම්, කකුල යාබද කකුල වන අතර කකුල ප්රතිවිරුද්ධයයි. ඉතින්, දැන් අපි ප්‍රශ්නයට පිළිතුරු දෙමු: කෝණයක සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් මොනවාද?

කෝණයක සයින්කර්ණයට ප්රතිවිරුද්ධ (දුර) කකුලේ අනුපාතය වේ.

අපේ ත්රිකෝණයේ.

කෝණයක කෝසයින්- මෙය යාබද (සමීප) කකුලේ කර්ණයට අනුපාතයයි.

අපේ ත්රිකෝණයේ.

කෝණ ස්පර්ශකය- මෙය ප්‍රතිවිරුද්ධ (දුර) කකුලේ යාබද (සමීප) අනුපාතයයි.

අපේ ත්රිකෝණයේ.

කෝණයක කෝටැන්ජන්ට්- මෙය යාබද (සමීප) කකුලේ ප්‍රතිවිරුද්ධ (දුර) අනුපාතයයි.

අපේ ත්රිකෝණයේ.

මෙම නිර්වචන අවශ්ය වේ මතක තබා ගන්න! කුමන කකුලෙන් බෙදිය යුතුද යන්න මතක තබා ගැනීම පහසු කිරීම සඳහා, ඔබ එය පැහැදිලිව තේරුම් ගත යුතුය ස්පර්ශකහා කෝටෙන්ජන්ට්කකුල් පමණක් වාඩි වන අතර, උපකල්පනය දිස්වන්නේ එහි පමණි සයිනස්හා කොසයින්. එවිට ඔබට සංගම් දාමයක් ඉදිරිපත් කළ හැකිය. උදාහරණයක් ලෙස, මෙය:

කොසයින්→ස්පර්ශ→ස්පර්ශ→යාබද;

කෝටැන්ජන්ට්→ස්පර්ශ→ස්පර්ශ→යාබද.

පළමුවෙන්ම, ත්‍රිකෝණයක පැතිවල අනුපාත ලෙස සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් මෙම පැතිවල දිග (එක් කෝණයකින්) මත රඳා නොපවතින බව මතක තබා ගත යුතුය. විශ්වාස කරන්න එපා? ඉන්පසු පින්තූරය දෙස බලා වග බලා ගන්න:

උදාහරණයක් ලෙස, කෝණයක කෝසයිනය සලකා බලන්න. නිර්වචනය අනුව, ත්‍රිකෝණයකින්: , නමුත් අපට ත්‍රිකෝණයකින් කෝණයක කෝසයිනය ගණනය කළ හැක: . ඔබට පෙනේ, පැතිවල දිග වෙනස් වේ, නමුත් එක් කෝණයක කෝසයිනයේ අගය සමාන වේ. මේ අනුව, සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් වල අගයන් රඳා පවතින්නේ කෝණයේ විශාලත්වය මත පමණි.

ඔබ අර්ථ දැක්වීම් තේරුම් ගන්නේ නම්, ඉදිරියට ගොස් ඒවා නිවැරදි කරන්න!

පහත රූපයේ දැක්වෙන ත්රිකෝණය සඳහා, අපි සොයා ගනිමු.

හොඳයි, ඔබට එය ලැබුණාද? ඉන්පසු එය ඔබම උත්සාහ කරන්න: කෙළවර සඳහා එකම ගණනය කරන්න.

ඒකක (ත්‍රිකෝණමිතික) කවය

අංශක සහ රේඩියනවල සංකල්ප තේරුම් ගැනීම, අපි සමාන අරයක් සහිත කවයක් සලකා බැලුවෙමු. එවැනි කවයක් ලෙස හැඳින්වේ තනි. ත්‍රිකෝණමිතිය අධ්‍යයනය කිරීමේදී එය ඉතා ප්‍රයෝජනවත් වේ. එමනිසා, අපි එය තව ටිකක් විස්තරාත්මකව වාසය කරමු.

ඔබට පෙනෙන පරිදි, මෙම කවය ගොඩනගා ඇත්තේ Cartesian ඛණ්ඩාංක පද්ධතිය තුළය. රවුමේ අරය එකකට සමාන වන අතර, රවුමේ කේන්ද්‍රය මූලාරම්භයේ පිහිටා ඇති අතර, අරය දෛශිකයේ ආරම්භක ස්ථානය අක්ෂයේ ධනාත්මක දිශාව දිගේ සවි කර ඇත (අපගේ උදාහරණයේ, මෙය අරය වේ).

රවුමේ සෑම ලක්ෂයක්ම සංඛ්යා දෙකකට අනුරූප වේ: අක්ෂය දිගේ ඛණ්ඩාංකය සහ අක්ෂය දිගේ ඛණ්ඩාංකය. මෙම ඛණ්ඩාංක අංක මොනවාද? පොදුවේ ගත් කල, ඔවුන් අත ඇති මාතෘකාව සමඟ කළ යුත්තේ කුමක්ද? මෙය සිදු කිරීම සඳහා, සලකා බැලූ සෘජු කෝණික ත්රිකෝණය ගැන මතක තබා ගන්න. ඉහත රූපයේ, ඔබට සම්පූර්ණ දකුණු ත්‍රිකෝණ දෙකක් දැකිය හැකිය. ත්රිකෝණයක් සලකා බලන්න. එය අක්ෂයට ලම්බක වන බැවින් එය සෘජුකෝණාස්රාකාර වේ.

ත්රිකෝණයක සිට සමාන වන්නේ කුමක් ද? ඒක හරි. ඊට අමතරව, ඒකක කවයේ අරය බව අපි දනිමු, එබැවින්, . මෙම අගය අපගේ කෝසයින් සූත්‍රයට ආදේශ කරන්න. මෙන්න මෙහෙමයි වෙන්නේ:

සහ ත්රිකෝණයක සිට සමාන වන්නේ කුමක් ද? හොඳයි, ඇත්ත වශයෙන්ම, ! මෙම සූත්‍රයට අරයේ අගය ආදේශ කර ලබා ගන්න:

ඉතින්, රවුමට අයත් ලක්ෂ්‍යයක ඛණ්ඩාංක මොනවාදැයි මට කියන්න පුළුවන්ද? හොඳයි, කොහෙත්ම නැහැ? ඔබ එය තේරුම් ගෙන ඉලක්කම් පමණක් නම්? එය අනුරූප වන්නේ කුමන ඛණ්ඩාංකයටද? හොඳයි, ඇත්ත වශයෙන්ම, සම්බන්ධීකරණය! එය අනුරූප වන්නේ කුමන ඛණ්ඩාංකයටද? ඒක හරි, සම්බන්ධීකරණය! මේ අනුව, කාරණය.

එවිට සමාන වන්නේ කුමක්ද සහ? ඒක හරි, අපි ස්පර්ශක සහ කෝටැන්ජන්ට් වල සුදුසු නිර්වචන භාවිතා කර එය ලබා ගනිමු, a.

කෝණය විශාල නම් කුමක් කළ යුතුද? මෙන්න, උදාහරණයක් ලෙස, මෙම පින්තූරයේ මෙන්:

තුළ වෙනස් වී ඇති දේ මෙම උදාහරණය? අපි එය තේරුම් ගනිමු. මෙය සිදු කිරීම සඳහා, අපි නැවතත් සෘජුකෝණාස්රාකාර ත්රිකෝණයකට හැරෙමු. සෘජුකෝණාස්රාකාර ත්රිකෝණයක් සලකා බලන්න: කෝණයක් (කෝණයට යාබදව). කෝණයක සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් වල වටිනාකම කොපමණද? ඒක හරි, අපි ත්‍රිකෝණමිතික ශ්‍රිතවල අනුරූප නිර්වචනවලට අනුගත වෙමු:

හොඳයි, ඔබට පෙනෙන පරිදි, කෝණයෙහි සයින් අගය තවමත් ඛණ්ඩාංකයට අනුරූප වේ; කෝණයෙහි කෝසයිනයේ අගය - ඛණ්ඩාංකය; සහ ස්පර්ශක සහ කෝටැන්ජන්ට් අගයන් අනුරූප අනුපාතවලට. මේ අනුව, මෙම සම්බන්ධතා අරය දෛශිකයේ ඕනෑම භ්‍රමණයකට අදාළ වේ.

අරය දෛශිකයේ ආරම්භක පිහිටීම අක්ෂයේ ධනාත්මක දිශාව ඔස්සේ බව දැනටමත් සඳහන් කර ඇත. මෙතෙක් අපි මෙම දෛශිකය වාමාවර්තව කරකවා ඇත, නමුත් අපි එය දක්ෂිණාවර්තව කරකවන්නේ නම් කුමක් සිදුවේද? අසාමාන්ය කිසිවක් නැත, ඔබට යම් ප්රමාණයක කෝණයක් ද ලැබෙනු ඇත, නමුත් එය පමණක් සෘණාත්මක වනු ඇත. මේ අනුව, අරය දෛශිකය වාමාවර්තව භ්රමණය කරන විට, අපි ලබා ගනිමු ධනාත්මක කෝණ, සහ දක්ෂිණාවර්තව කැරකෙන විට - සෘණ.

එබැවින්, රවුම වටා ඇති අරය දෛශිකයේ සම්පූර්ණ විප්ලවයක් හෝ බව අපි දනිමු. අරය දෛශිකය මගින් හෝ කරකැවිය හැකිද? හොඳයි, ඇත්තෙන්ම ඔබට පුළුවන්! පළමු අවස්ථාවේ දී, එබැවින්, අරය දෛශිකය එක් සම්පූර්ණ විප්ලවයක් සිදු කර ස්ථානයේ හෝ නතර වනු ඇත.

දෙවන අවස්ථාවේ දී, එනම් අරය දෛශිකය සම්පූර්ණ විප්ලව තුනක් සිදු කර ස්ථානයේ හෝ නතර වනු ඇත.

මේ අනුව, ඉහත උදාහරණ වලින්, අපට නිගමනය කළ හැක්කේ කෝණ මගින් වෙනස් වන හෝ (ඕනෑම පූර්ණ සංඛ්‍යාවක් ඇති) අරය දෛශිකයේ එකම ස්ථානයට අනුරූප වන බවයි.

පහත රූපයේ කෝණයක් පෙන්වයි. එම රූපයම කෙළවරට අනුරූප වේ, සහ එසේ ය. මෙම ලැයිස්තුව දින නියමයක් නොමැතිව දිගටම කරගෙන යා හැක. මෙම සියලු කෝණ සාමාන්‍ය සූත්‍රය හෝ (ඕනෑම නිඛිලයක් ඇති තැන) සමඟ ලිවිය හැක.

දැන්, මූලික ත්‍රිකෝණමිතික ශ්‍රිතවල අර්ථ දැක්වීම් දැනගෙන ඒකක කවය භාවිතා කරමින්, අගයන් සමාන වන්නේ කුමක් දැයි පිළිතුරු දීමට උත්සාහ කරන්න:

මෙන්න ඔබට උදවු කිරීමට ඒකක කවයක්:

කිසියම් දුෂ්කරතාවයක් තිබේද? එහෙනම් අපි එය තේරුම් ගනිමු. එබැවින් අපි එය දනිමු:

මෙතැන් සිට, අපි කෝණයේ ඇතැම් මිනුම් වලට අනුරූප වන ලක්ෂ්යවල ඛණ්ඩාංක තීරණය කරමු. හොඳයි, අපි පිළිවෙලට ආරම්භ කරමු: කෙළවරේ ඛණ්ඩාංක සහිත ලක්ෂ්‍යයකට අනුරූප වේ, එබැවින්:

නොපවතී;

තවද, එකම තර්කනයට අනුකූලව, කොන් පිළිවෙලින් ඛණ්ඩාංක සහිත ලකුණු වලට අනුරූප වන බව අපි සොයා ගනිමු. මෙය දැන ගැනීමෙන්, අනුරූප ලක්ෂ්යවල ත්රිකෝණමිතික ශ්රිතවල අගයන් තීරණය කිරීම පහසුය. පළමුව ඔබම උත්සාහ කරන්න, පසුව පිළිතුරු පරීක්ෂා කරන්න.

පිළිතුරු:

නොපවතී

නොපවතී

නොපවතී

නොපවතී

මේ අනුව, අපට පහත වගුව සෑදිය හැකිය:

මෙම සියලු අගයන් මතක තබා ගැනීමට අවශ්ය නැත. ඒකක කවයේ ලක්ෂ්‍ය ඛණ්ඩාංක සහ ත්‍රිකෝණමිතික ශ්‍රිතවල අගයන් අතර ලිපි හුවමාරුව මතක තබා ගැනීම ප්‍රමාණවත් වේ:

නමුත් පහත වගුවේ දක්වා ඇති කෝණවල ත්‍රිකෝණමිතික ශ්‍රිතවල අගයන් සහ, මතක තබා ගත යුතුය:

බිය නොවන්න, දැන් අපි එක් උදාහරණයක් පෙන්වන්නෙමු අනුරූප අගයන් වෙනුවට සරල කටපාඩම් කිරීම:

මෙම ක්රමය භාවිතා කිරීම සඳහා, සියලු දෙනා සඳහා සයින් අගයන් මතක තබා ගැනීම වැදගත් වේ පියවර තුනක්කෝණය (), මෙන්ම කෝණයේ ස්පර්ශක අගය. මෙම අගයන් දැන ගැනීමෙන්, සම්පූර්ණ වගුව නැවත යථා තත්ත්වයට පත් කිරීම තරමක් පහසුය - කෝසයින් අගයන් ඊතල වලට අනුකූලව මාරු කරනු ලැබේ, එනම්:

මෙය දැන ගැනීමෙන්, ඔබට අගයන් නැවත ලබා ගත හැකිය. " " ඉලක්කම් ගැළපෙන අතර " " හරය ගැළපේ. රූපයේ දැක්වෙන ඊතල වලට අනුකූලව කෝටැන්ජන්ට් අගයන් මාරු කරනු ලැබේ. ඔබ මෙය තේරුම් ගෙන ඊතල සහිත රූප සටහන මතක තබා ගන්නේ නම්, මේසයෙන් සම්පූර්ණ අගය මතක තබා ගැනීමට එය ප්රමාණවත් වනු ඇත.

රවුමක ලක්ෂ්‍යයක ඛණ්ඩාංක

රවුමක ලක්ෂ්‍යයක් (එහි ඛණ්ඩාංක) සොයා ගත හැකිද, රවුමේ කේන්ද්‍රයේ ඛණ්ඩාංක, එහි අරය සහ භ්‍රමණ කෝණය දැන ගැනීම?

හොඳයි, ඇත්තෙන්ම ඔබට පුළුවන්! එලියට ගේමු සාමාන්ය සූත්රයලක්ෂ්‍යයක ඛණ්ඩාංක සොයා ගැනීමට.

මෙන්න, උදාහරණයක් ලෙස, අපට එවැනි කවයක් තිබේ:

ලක්ෂ්යය රවුමේ කේන්ද්රය බව අපට ලබා දී ඇත. රවුමේ අරය සමාන වේ. ලක්ෂ්‍යය අංශක වලින් භ්‍රමණය කිරීමෙන් ලබාගත් ලක්ෂ්‍යයේ ඛණ්ඩාංක සොයා ගැනීම අවශ්‍ය වේ.

රූපයෙන් දැකිය හැකි පරිදි, ලක්ෂ්යයේ ඛණ්ඩාංකය කොටසෙහි දිගට අනුරූප වේ. කොටසෙහි දිග රවුමේ කේන්ද්රයේ ඛණ්ඩාංකයට අනුරූප වේ, එනම් එය සමාන වේ. කොසයින් අර්ථ දැක්වීම භාවිතයෙන් කොටසක දිග ප්‍රකාශ කළ හැක:

එවිට අපට ඛණ්ඩාංකය යන කරුණ සඳහා එය තිබේ.

එම තර්කයෙන්ම, ලක්ෂ්‍යය සඳහා y ඛණ්ඩාංකයේ අගය අපට සොයාගත හැකිය. මේ ක්රමයෙන්,

ඉතින් ඇතුලට සාමාන්ය දැක්මලක්ෂ්ය ඛණ්ඩාංක සූත්ර මගින් තීරණය කරනු ලැබේ:

කව මධ්යස්ථාන ඛණ්ඩාංක,

රවුම් අරය,

අරය දෛශිකයේ භ්රමණ කෝණය.

ඔබට පෙනෙන පරිදි, අප සලකා බලන ඒකක කවය සඳහා, මෙම සූත්‍ර සැලකිය යුතු ලෙස අඩු වී ඇත, මන්ද මධ්‍යයේ ඛණ්ඩාංක ශුන්‍ය වන අතර අරය එකකට සමාන වේ:

හොඳයි, රවුමක ලක්ෂ්‍ය සෙවීමට පුරුදු වෙමින් රසයක් සඳහා මෙම සූත්‍ර අත්හදා බලමුද?

1. ලක්ෂ්‍යයක් ක්‍රියාත්මක කිරීමෙන් ලබාගත් ඒකක කවයක් මත ලක්ෂ්‍යයක ඛණ්ඩාංක සොයන්න.

2. ලක්ෂ්‍යයක් භ්‍රමණය කිරීමෙන් ලබාගත් ඒකක කවයක් මත ලක්ෂ්‍යයක ඛණ්ඩාංක සොයන්න.

3. ලක්ෂ්‍යයක් ක්‍රියාත්මක කිරීමෙන් ලබාගත් ඒකක කවයක් මත ලක්ෂ්‍යයක ඛණ්ඩාංක සොයන්න.

4. ලක්ෂ්යය - රවුමේ කේන්ද්රය. රවුමේ අරය සමාන වේ. මගින් ආරම්භක අරය දෛශිකය කරකැවීමෙන් ලබාගත් ලක්ෂ්යයේ ඛණ්ඩාංක සොයා ගැනීම අවශ්ය වේ.

5. ලක්ෂ්යය - රවුමේ කේන්ද්රය. රවුමේ අරය සමාන වේ. මගින් ආරම්භක අරය දෛශිකය කරකැවීමෙන් ලබාගත් ලක්ෂ්යයේ ඛණ්ඩාංක සොයා ගැනීම අවශ්ය වේ.

රවුමක ලක්ෂ්‍යයක ඛණ්ඩාංක සොයා ගැනීමේ ගැටලුවක් තිබේද?

මෙම උදාහරණ පහ විසඳන්න (නැතහොත් විසඳුම හොඳින් තේරුම් ගන්න) එවිට ඔබ ඒවා සොයා ගන්නේ කෙසේදැයි ඉගෙන ගනු ඇත!

1.

එය දැක ගත හැකිය. ආරම්භක ලක්ෂ්‍යයේ සම්පූර්ණ හැරීමකට අනුරූප වන දේ අපි දනිමු. මේ අනුව, අපේක්ෂිත ලක්ෂ්යය හැරෙන විට එම ස්ථානයේම පවතිනු ඇත. මෙය දැන ගැනීමෙන්, ලක්ෂ්‍යයේ අපේක්ෂිත ඛණ්ඩාංක අපට හමු වේ:

2. කවය යනු ලක්ෂ්‍යයක කේන්ද්‍රයක් සහිත ඒකකයකි, එයින් අදහස් කරන්නේ අපට සරල කළ සූත්‍ර භාවිතා කළ හැකි බවයි:

එය දැක ගත හැකිය. ආරම්භක ලක්ෂ්‍යයේ සම්පූර්ණ භ්‍රමණ දෙකකට අනුරූප වන දේ අපි දනිමු. මේ අනුව, අපේක්ෂිත ලක්ෂ්යය හැරෙන විට එම ස්ථානයේම පවතිනු ඇත. මෙය දැන ගැනීමෙන්, ලක්ෂ්‍යයේ අපේක්ෂිත ඛණ්ඩාංක අපට හමු වේ:

සයින් සහ කොසයින් වේ වගු අගයන්. අපි ඔවුන්ගේ වටිනාකම් මතක තබා ගන්නෙමු:

මේ අනුව, අපේක්ෂිත ලක්ෂ්යයට ඛණ්ඩාංක ඇත.

3. කවය යනු ලක්ෂ්‍යයක කේන්ද්‍රයක් සහිත ඒකකයකි, එයින් අදහස් කරන්නේ අපට සරල කළ සූත්‍ර භාවිතා කළ හැකි බවයි:

එය දැක ගත හැකිය. රූපයේ සලකා බැලූ උදාහරණය නිරූපණය කරමු:

අරය සහ සමාන අක්ෂය සහිත කෝණ සාදයි. කොසයින් සහ සයින් වල වගු අගයන් සමාන බව දැනගෙන, මෙහි කෝසයිනය ගන්නා බව තීරණය කිරීමෙන් සෘණ අර්ථය, සහ සයින් ධනාත්මක වේ, අපට ඇත්තේ:

මාතෘකාවේ ත්රිකෝණමිතික ශ්රිතයන් අඩු කිරීම සඳහා සූත්ර අධ්යයනය කිරීමේදී සමාන උදාහරණ වඩාත් විස්තරාත්මකව විශ්ලේෂණය කෙරේ.

මේ අනුව, අපේක්ෂිත ලක්ෂ්යයට ඛණ්ඩාංක ඇත.

4.

අරය දෛශිකයේ භ්‍රමණ කෝණය (තත්ත්වය අනුව)

සයින් සහ කොසයින් වල අනුරූප සලකුණු තීරණය කිරීම සඳහා, අපි ඒකක කවයක් සහ කෝණයක් සාදන්නෙමු:

ඔබට පෙනෙන පරිදි, අගය, එනම්, ධනාත්මක වන අතර, අගය, එනම්, සෘණ වේ. අනුරූප ත්රිකෝණමිතික ශ්රිතවල වගු අගයන් දැන ගැනීමෙන්, අපි එය ලබා ගනිමු:

ලබාගත් අගයන් අපගේ සූත්‍රයට ආදේශ කර ඛණ්ඩාංක සොයා ගනිමු:

මේ අනුව, අපේක්ෂිත ලක්ෂ්යයට ඛණ්ඩාංක ඇත.

5. මෙම ගැටළුව විසඳීම සඳහා, අපි සාමාන්‍ය ස්වරූපයෙන් සූත්‍ර භාවිතා කරමු, එහිදී

රවුමේ කේන්ද්‍රයේ ඛණ්ඩාංක (අපගේ උදාහරණයේ,

කව අරය (තත්ත්වය අනුව)

අරය දෛශිකයේ භ්රමණ කෝණය (තත්ත්වය අනුව).

සියලුම අගයන් සූත්‍රයට ආදේශ කර ලබා ගන්න:

සහ - වගු අගයන්. අපි ඒවා මතක තබා ගෙන ඒවා සූත්‍රයට ආදේශ කරමු:

මේ අනුව, අපේක්ෂිත ලක්ෂ්යයට ඛණ්ඩාංක ඇත.

සාරාංශය සහ මූලික සූත්‍රය

කෝණයක සයින් යනු ප්‍රතිවිරුද්ධ (දුර) කකුලේ කර්ණයට අනුපාතයයි.

කෝණයක කෝසයින් යනු යාබද (සමීප) කකුලේ කර්ණයට අනුපාතයයි.

කෝණයක ස්පර්ශකය යනු ප්රතිවිරුද්ධ (දුර) පාදයේ යාබද (සමීප) අනුපාතයයි.

කෝණයක කෝටැන්ජන්ට් යනු යාබද (සමීප) කකුලේ ප්‍රතිවිරුද්ධ (දුර) අනුපාතයයි.

කෝණ 0, 30, 45, 60, 90, ... අංශක සඳහා මූලික ත්‍රිකෝණමිතික ශ්‍රිත වගුව

$\sin$, $\cos$, $\tan$, සහ $\cot$ යන ශ්‍රිතවල ත්‍රිකෝණමිතික නිර්වචන වලින් කෙනෙකුට $0$ සහ $90$ අංශක කෝණ සඳහා ඒවායේ අගයන් සොයාගත හැක:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ අර්ථ දක්වා නැත;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ අර්ථ දක්වා නැත.

පාසල් ජ්‍යාමිතික පාඨමාලාවේදී සෘජුකෝණාස්‍ර ත්‍රිකෝණ අධ්‍යයනය කිරීමේදී $0°$, $30°$, $45°$, $60°$ සහ $90°$ යන කෝණවල ත්‍රිකෝණමිතික ශ්‍රිත දක්නට ලැබේ.

අංශක සහ රේඩියනවල නිශ්චිත කෝණ සඳහා ත්‍රිකෝණමිතික ශ්‍රිතවල සොයාගත් අගයන් ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ කටපාඩම් කිරීමේ සහ භාවිතයේ පහසුව සඳහා pi)(3) $, $\frac(\pi)(2)$) යනුවෙන් හැඳින්වෙන වගුවක ඇතුළත් කර ඇත. ත්රිකෝණමිතික වගුව, ත්රිකෝණමිතික ශ්රිතවල මූලික අගයන් වගුවආදිය

අඩු කිරීමේ සූත්‍ර භාවිතා කරන විට, ත්‍රිකෝණමිතික වගුව පිළිවෙලින් $360°$ සහ $2\pi$ රේඩියන කෝණයක් දක්වා පුළුල් කළ හැක:

ත්‍රිකෝණමිතික ශ්‍රිතවල ආවර්තිතා ගුණ යෙදීමෙන්, දැනටමත් දන්නා එකකින් ඩොලර් 360°$ කින් වෙනස් වන සෑම කෝණයක්ම ගණනය කර වගුවක සටහන් කළ හැක. උදාහරණයක් ලෙස, $0°$ කෝණය සඳහා ත්‍රිකෝණමිතික ශ්‍රිතය $0°+360°$ කෝණය සඳහාත්, $0°+2 \cdot 360°$ කෝණය සඳහාත්, සහ $0°+3 කෝණය සඳහාත් එකම අගයක් ඇත. cdot 360°$ සහ ආදිය.

ත්‍රිකෝණමිතික වගුවක් භාවිතා කරමින්, ඔබට ඒකක රවුමක සියලුම කෝණවල අගයන් තීරණය කළ හැකිය.

පාසල් ජ්‍යාමිතික පාඨමාලාවේදී, ත්‍රිකෝණමිතික ගැටළු විසඳීමේ පහසුව සඳහා ත්‍රිකෝණමිතික වගුවක එකතු කර ඇති ත්‍රිකෝණමිතික ශ්‍රිතවල මූලික අගයන් කටපාඩම් කළ යුතුය.

මේසයක් භාවිතා කිරීම

වගුවෙහි, අවශ්ය ත්රිකෝණමිතික ශ්රිතය සහ මෙම ශ්රිතය ගණනය කිරීමට අවශ්ය වන කෝණයෙහි හෝ රේඩියනයේ අගය සොයා ගැනීමට ප්රමාණවත් වේ. ශ්‍රිතය සමඟ පේළියේ සහ අගය සහිත තීරුවේ ඡේදනය වන විට, දී ඇති තර්කයේ ත්‍රිකෝණමිතික ශ්‍රිතයේ අපේක්ෂිත අගය අපට ලැබේ.

රූපයේ ඔබට $\frac(1)(2)$ ට සමාන $\cos⁡60°$ අගය සොයා ගන්නා ආකාරය දැක ගත හැක.

විස්තීරණ ත්‍රිකෝණමිතික වගුව ද එලෙසම භාවිතා වේ. එය භාවිතා කිරීමේ වාසිය නම්, දැනටමත් සඳහන් කර ඇති පරිදි, ඕනෑම කෝණයක පාහේ ත්රිකෝණමිතික ශ්රිතය ගණනය කිරීමයි. උදාහරණයක් ලෙස, ඔබට $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 යන අගය පහසුවෙන් සොයාගත හැක. °$:

මූලික ත්‍රිකෝණමිතික ශ්‍රිතවල බ්‍රැඩිස් වගු

අංශක නිඛිල අගයක් සහ මිනිත්තු ගණනක නිඛිල අගයක් සඳහා නිරපේක්ෂ ඕනෑම කෝණ අගයක ත්‍රිකෝණමිතික ශ්‍රිතය ගණනය කිරීමේ හැකියාව බ්‍රැඩිස් වගු භාවිතා කරයි. උදාහරණයක් ලෙස, $\cos⁡34°7"$ අගය සොයා ගන්න. වගු කොටස් 2කට බෙදා ඇත: $\sin$ සහ $\cos$ අගයන් සහ $\tan$ සහ $\ වගුව cot$ අගයන්.

බ්‍රැඩිස් වගු මඟින් දශම ස්ථාන 4ක් දක්වා නිරවද්‍යතාවයකින් ත්‍රිකෝණමිතික ශ්‍රිතවල ආසන්න අගයක් ලබා ගැනීමට හැකි වේ.

Bradis වගු භාවිතා කිරීම

සයින් සඳහා බ්‍රැඩිස් වගු භාවිතා කරමින්, අපි සොයා ගන්නේ $\sin⁡17°42"$. මෙය සිදු කිරීම සඳහා, සයින් සහ කොසයින වගුවේ වම්පස ඇති තීරුවේ අංශකවල අගය - $17°$, සහ ඉහළම පේළිය මිනිත්තු වල අගය සොයා ගනී - $42"$. ඔවුන්ගේ මංසන්ධියේදී, අපට අපේක්ෂිත අගය ලැබේ:

$\sin17°42"=0.304$.

$\sin17°44"$ හි අගය සොයා ගැනීමට, ඔබ මේසයේ දකුණු පැත්තේ ඇති නිවැරදි කිරීම භාවිතා කළ යුතුය. මෙම නඩුවවගුවේ ඇති $42"$ අගයට, ඔබ $2"$ සඳහා නිවැරදි කිරීමක් එක් කළ යුතු අතර එය $0.0006$ ට සමාන වේ. අපට ලැබෙන්නේ:

$\sin17°44"=0.304+0.0006=0.3046$.

$\sin17°47"$ හි අගය සොයා ගැනීමට, අපි මේසයේ දකුණු පැත්තේ ඇති නිවැරදි කිරීම ද භාවිතා කරමු, මෙම අවස්ථාවේදී පමණක් අපි $\sin17°48"$ අගය පදනමක් ලෙස ගෙන නිවැරදි කිරීම අඩු කරමු. $1"$:

$\sin17°47"=0.3057-0.0003=0.3054$.

කෝසයින ගණනය කිරීමේදී, අපි සමාන ක්රියාවන් සිදු කරයි, නමුත් අපි දකුණු තීරුවේ අංශක සහ මේසයේ පහළ තීරුවේ මිනිත්තු දෙස බලමු. උදාහරණයක් ලෙස, $\cos20°=0.9397$.

$90°$ දක්වා ස්පර්ශක අගයන් සහ කුඩා කෝණ කෝටැන්ජන්ට් සඳහා නිවැරදි කිරීම් නොමැත. උදාහරණයක් ලෙස, අපි $\tan 78°37"$ සොයා ගනිමු, එය වගුවට අනුව $4,967$ වේ.

ලිපියෙහි, එය පෙනෙන්නේ කෙසේද යන්න අපි සම්පූර්ණයෙන්ම තේරුම් ගනිමු වගුව ත්රිකෝණමිතික අගයන්, sine, cosine, tangent සහ cotangent. අංශක 0,30,45,60,90,...,360 කෝණයකින් ත්‍රිකෝණමිතික ශ්‍රිතවල මූලික අගය සලකා බලන්න. ත්‍රිකෝණමිතික ශ්‍රිතවල අගය ගණනය කිරීමේදී මෙම වගු භාවිතා කරන්නේ කෙසේදැයි බලමු.
මුලින්ම සලකා බලන්න කොසයින්, සයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් වගුව 0, 30, 45, 60, 90,.. අංශක කෝණයකින්. මෙම ප්‍රමාණවල නිර්වචනය අංශක 0 සහ 90 කෝණවල ශ්‍රිතවල අගය තීරණය කිරීමට හැකි වේ:

sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, 00 හි කෝටැන්ජන්ට් නිර්වචනය නොකෙරේ
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0 හි ස්පර්ශකය නිර්වචනය නොවේ

අපි අංශක 30 සිට 90 දක්වා කෝණ සහිත සෘජු කෝණික ත්රිකෝණ ගතහොත්. අපට ලැබෙන්නේ:

sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3

අපි පෝරමයේ ලබාගත් සියලුම අගයන් නියෝජනය කරමු ත්රිකෝණමිතික වගුව:

සයින්, කෝසයින, ස්පර්ශක සහ කෝටැන්ජන්ට් වගුව!

අපි වාත්තු සූත්‍රය භාවිතා කරන්නේ නම්, අපගේ වගුව වැඩි වනු ඇත, අංශක 360 දක්වා කෝණ සඳහා අගයන් එකතු වේ. එය පෙනෙනු ඇත:

එසේම, ආවර්තිතා ගුණාංග මත පදනම්ව, අපි කෝණ 0 0 +360 0 *z .... 330 0 +360 0 *z කින් ප්‍රතිස්ථාපනය කළහොත් වගුව වැඩි කළ හැක, එහි z නිඛිලයක් වේ. මෙම වගුවේ, තනි රවුමක ලක්ෂ්යවලට අනුරූප වන සියලුම කෝණවල අගය ගණනය කළ හැකිය.

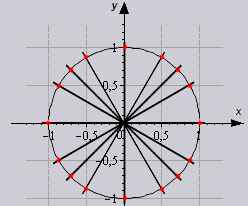
විසඳුමේ වගුව භාවිතා කරන්නේ කෙසේදැයි අපි පැහැදිලිව බලමු.
සෑම දෙයක්ම ඉතා සරලයි. අපට අවශ්‍ය අගය අපට අවශ්‍ය සෛලවල ඡේදනය වන ස්ථානයේ පවතින බැවින්. උදාහරණයක් ලෙස, අපි අංශක 60 ක කෝණයක් ගනිමු, වගුවේ එය මේ ආකාරයෙන් පෙනෙනු ඇත:

ත්‍රිකෝණමිතික ශ්‍රිතවල ප්‍රධාන අගයන්හි අවසාන වගුවේ අපි ක්‍රියා කරන්නේ එකම ආකාරයටයි. නමුත් මෙම වගුවේ අංශක 1020 ක කෝණයකින් ස්පර්ශක අගය කොපමණ දැයි සොයා ගැනීමට හැකි වේ, එය = -√3 අපි 1020 0 = 300 0 +360 0 *2 පරීක්ෂා කරමු. අපි මේසය සොයා ගනිමු.

බ්රැඩිස් මේසය. සයින්, කෝසයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් සඳහා.

බ්‍රැඩිස් වගු කොටස් කිහිපයකට බෙදා ඇත, ඒවා කොසයින් සහ සයින්, ස්පර්ශක සහ කෝටැන්ජන්ට් වගු වලින් සමන්විත වේ - එය කොටස් දෙකකට බෙදා ඇත (අංශක 90 දක්වා කෝණයක tg සහ කුඩා කෝණවල ctg).

සයින් සහ කොසයින්

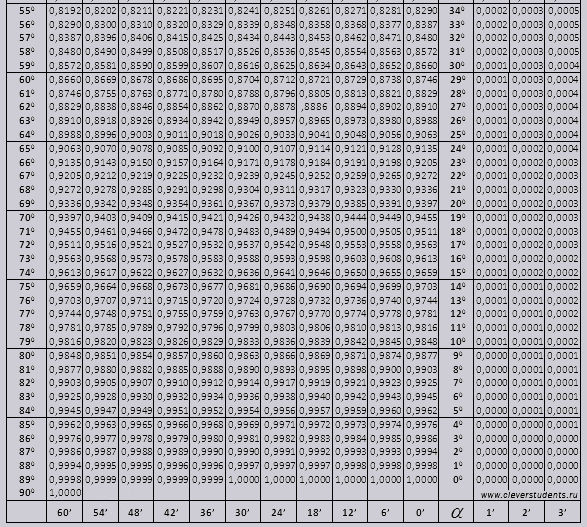
කෝණය tg 00 සිට 760 දක්වා, කෝණය ctg 140 සිට 900 දක්වා.

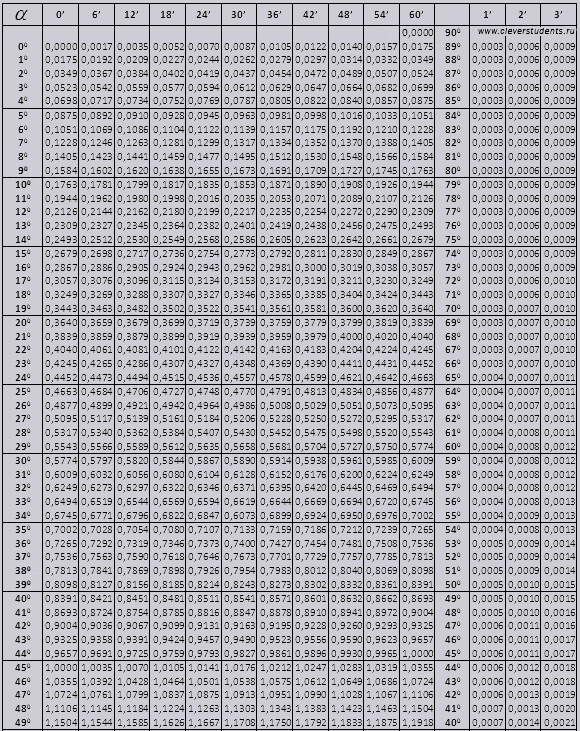
tg 900 දක්වා සහ ctg කුඩා කෝණ.

ගැටළු විසඳීමේදී බ්‍රැඩිස් වගු භාවිතා කරන්නේ කෙසේදැයි සොයා බලමු.

අපි තනතුරු පාපය (වම් දාරයේ සිට තීරුවේ නම් කිරීම) මිනිත්තු 42 (නම් කිරීම ඉහළ පේළියේ ඇත) සොයා ගනිමු. තරණය කිරීමෙන් අපි තනතුරක් සොයන්නෙමු, එය = 0.3040 වේ.

මිනිත්තු වල අගයන් මිනිත්තු හයක පරතරයකින් දක්වා ඇත, අපට අවශ්‍ය අගය මෙම පරතරය තුළට වැටෙන්නේ නම් කුමක් කළ යුතුද? අපි විනාඩි 44 ක් ගත කරමු, මේසයේ ඇත්තේ 42 ක් පමණි, අපි 42 පදනමක් ලෙස ගෙන අමතර තීරු භාවිතා කරමු. දකුණු පැත්ත, අපි 2 වන සංශෝධනය ගෙන 0.3040 + 0.0006 එකතු කළ විට අපට 0.3046 ලැබේ.

sin 47 min සමඟ, අපි පදනමක් ලෙස 48 min ගෙන එයින් නිවැරදි කිරීම් 1 ක් අඩු කරමු, එනම් 0.3057 - 0.0003 = 0.3054

cos ගණනය කිරීමේදී, අපි පාපයට සමානව වැඩ කරමු, අපි මේසයේ පහළ පේළිය පමණක් පදනම ලෙස ගනිමු. උදාහරණයක් ලෙස cos 20 0 = 0.9397

90 0 දක්වා කෝණයක tg අගයන් සහ කුඩා කෝණයක ඇඳෙහි අගයන් නිවැරදි වන අතර ඒවායේ නිවැරදි කිරීම් නොමැත. උදාහරණයක් ලෙස, tg 78 0 37min = 4.967 සොයා ගන්න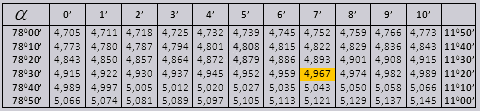


සහ ctg 20 0 13 min = 25.83

හොඳයි, මෙන්න අපි ප්රධාන ත්රිකෝණමිතික වගු සලකා බලමු. මෙම තොරතුරු ඔබට අතිශයින්ම ප්‍රයෝජනවත් වනු ඇතැයි අපි බලාපොරොත්තු වෙමු. වගු මත ඔබේ ප්‍රශ්න තිබේ නම්, අදහස් දැක්වීමේදී ලිවීමට වග බලා ගන්න!

සටහන: වෝල් ෆෙන්ඩර් - බිත්ති ආරක්ෂා කිරීම සඳහා ෆෙන්ඩර් පුවරුව. බිත්ති රහිත රාමු රහිත ෆෙන්ඩර් (http://www.spi-polymer.ru/otboyniki/) සබැඳිය අනුගමනය කර වැඩිදුර සොයා බලන්න.

ස්පර්ශක (tg x) සහ cotangent (ctg x) සඳහා යොමු දත්ත. ජ්යාමිතික නිර්වචනය, ගුණාංග, ප්රස්තාර, සූත්ර. ස්පර්ශක සහ කෝටැන්ජන්ට්, ව්‍යුත්පන්න, අනුකලනය, ශ්‍රේණි ප්‍රසාරණ වගුව. සංකීර්ණ විචල්‍ය හරහා ප්‍රකාශන. හයිපර්බෝලික් කාර්යයන් සමඟ සම්බන්ධ වීම.

ජ්යාමිතික අර්ථ දැක්වීම

|BD| - A ලක්ෂ්‍යයේ කේන්ද්‍රගත වූ රවුමක චාපයේ දිග.
α යනු රේඩියන වලින් ප්‍රකාශිත කෝණයයි.

ස්පර්ශක ( tgα) ඍජු ත්‍රිකෝණයක කර්ණය සහ පාදය අතර α කෝණය මත පදනම්ව ත්‍රිකෝණමිතික ශ්‍රිතයකි, ප්‍රතිවිරුද්ධ පාදයේ දිග අනුපාතයට සමාන |BC| යාබද කකුලේ දිගට |AB| .

කෝටැන්ජන්ට් ( ctgα) සෘජුකෝණාශ්‍රය ත්‍රිකෝණයක කර්ණය සහ පාදය අතර α කෝණය මත පදනම්ව ත්‍රිකෝණමිතික ශ්‍රිතයකි, යාබද පාදයේ දිග අනුපාතයට සමාන |AB| විරුද්ධ පාදයේ දිගට |BC| .

ස්පර්ශක

කොහෙද n- සමස්ත.

බටහිර සාහිත්‍යයේ ස්පර්ශය පහත පරිදි දැක්වේ.
.
;
;
.

ස්පර්ශක ශ්‍රිතයේ ප්‍රස්තාරය, y = tg x

කෝටැන්ජන්ට්

කොහෙද n- සමස්ත.

බටහිර සාහිත්‍යයේ කෝටැන්ජන්ට් පහත පරිදි දැක්වේ.
.
පහත සඳහන් අංකනය ද සම්මත කර ඇත:
;
;
.

කෝටැන්ජන්ට් ශ්‍රිතයේ ප්‍රස්තාරය, y = ctg x

ස්පර්ශක සහ කෝටැන්ජන්ට් වල ගුණ

ආවර්තිතා

කාර්යයන් y= tg xසහ y= ctg xπ කාල පරිච්ඡේදය සමඟ ආවර්තිතා වේ.

සමානාත්මතාවය

ස්පර්ශක සහ කෝටැන්ජන්ට් ශ්‍රිතය අමුතුයි.

නිර්වචනය සහ අගයන්හි වසම්, ආරෝහණ, අවරෝහණ

ස්පර්ශක සහ කෝටැන්ජන්ට් යන ශ්‍රිතයන් ඒවායේ නිර්වචන වසම මත අඛණ්ඩව පවතී (අඛණ්ඩත්වයේ සාධනය බලන්න). ස්පර්ශක සහ කෝටැන්ජන්ට් වල ප්‍රධාන ගුණාංග වගුවේ දක්වා ඇත ( n- පූර්ණ සංඛ්යාව).

	y= tg x	y= ctg x
විෂය පථය සහ අඛණ්ඩතාව
වටිනාකම් පරාසය	-∞ < y < +∞	-∞ < y < +∞
නැගීම		-
බැස යනවා	-
අන්ත	-	-
ශුන්‍ය, y= 0
y-අක්ෂය සමඟ ඡේදනය වීමේ ලක්ෂ්‍ය, x = 0	y= 0	-

සූත්ර

සයින් සහ කොසයින් අනුව ප්‍රකාශන

; ;
; ;
;

එකතුවේ සහ වෙනසෙහි ස්පර්ශක සහ කෝටැන්ජන්ට් සඳහා සූත්‍ර

උදාහරණයක් ලෙස, ඉතිරි සූත්‍ර පහසුවෙන් ලබා ගත හැකිය

ස්පර්ශක නිෂ්පාදනය

ස්පර්ශකවල එකතුව සහ වෙනස සඳහා සූත්‍රය

මෙම වගුව තර්කයේ සමහර අගයන් සඳහා ස්පර්ශක සහ කෝටැන්ජන්ට් වල අගයන් පෙන්වයි.

සංකීර්ණ සංඛ්‍යා අනුව ප්‍රකාශන

අධිබල ශ්‍රිත අනුව ප්‍රකාශන

;
;

ව්යුත්පන්න

; .

.
ශ්‍රිතයේ x විචල්‍යයට අදාළව n වන අනුපිළිවෙලෙහි ව්‍යුත්පන්නය:
.
ස්පර්ශක සඳහා සූත්‍ර ව්‍යුත්පන්න කිරීම >>> ; cotangent සඳහා >>>

අනුකලනය

මාලාවකට විස්තාරණය

x හි බලවල ස්පර්ශකයේ ප්‍රසාරණය ලබා ගැනීමට, ඔබ ප්‍රසාරණයේ නියමයන් කිහිපයක් ගත යුතුය. බල මාලාවකාර්යයන් සඳහා පාපය xහා cos xසහ මෙම බහුපද එකිනෙක බෙදන්න, . මෙය පහත සූත්‍ර ඇති කරයි.

හිදී .

හිදී .
කොහෙද බී එන්- බර්නූලි අංක. පුනරාවර්තන සම්බන්ධතාවයෙන් ඒවා තීරණය වේ:
;
;
කොහෙද .
හෝ Laplace සූත්රය අනුව:

ප්රතිලෝම ශ්රිත

ප්රතිලෝම ශ්රිතස්පර්ශක සහ කෝටැන්ජන්ට් පිළිවෙලින් ආක්ටැන්ජන්ට් සහ චාපටැන්ජන්ට් වේ.

ආක්ටේන්ජන්ට්, ආර්ක්ට්ජී

, කොහෙද n- සමස්ත.

චාප ස්පර්ශක, arcctg

, කොහෙද n- සමස්ත.

යොමු:
තුල. බ්‍රොන්ස්ටයින්, කේ.ඒ. Semendyaev, ඉංජිනේරුවන් සහ උසස් අධ්‍යාපන ආයතනවල සිසුන් සඳහා ගණිත අත්පොත, Lan, 2009.
G. Korn, පර්යේෂකයන් සහ ඉංජිනේරුවන් සඳහා ගණිත අත්පොත, 2012.