Число різних розміщень. Основні формули комбінаторики. Комбінаторика: формула перестановки, розміщення

Перестановки. Формула для числа перестановок

Перестановки з n елементів

Нехай безліч Хскладається з n елементів.

Визначення. Розміщення без повторень зn елементів множиниX по n називається перестановкою з n елементів.

Зауважимо, що в будь-яку перестановку входять усі елементи множиниХ , причому по одному разу. Тобто перестановки одна від одної відрізняються лише порядком проходження елементів і можуть вийти одна з іншої перестановкою елементів (звідси і назва).

Число всіх перестановок зn елементів позначається символом .

Оскільки перестановки – це окремий випадокрозміщень без повторень при , то формулу для знаходження числа отримаємо з формули (2), підставляючи до неї :

Таким чином,

(3)

приклад. Скільки можна розмістити на полиці 5 книг?

Рішення. Способів розміщення книг на полиці існує стільки, скільки існує різних перестановок із п'яти елементів:методів.

Зауваження. Формули (1)-(3) запам'ятовувати необов'язково: завдання їх застосування завжди можна вирішити з допомогою правила твори. Якщо в учнів існують проблеми зі складанням комбінаторних моделей завдань, то краще зробити вужчим безліч використовуваних формул і правил (щоб було менше можливості помилитися). Щоправда, завдання, у яких використовуються перестановки та формула (3), зазвичай вирішуються без особливих проблем.

Завдання

1. Ф. Скільки способами можуть стати черга в квиткову касу: 1) 3 людини; 2) 5 чоловік?

Рішення.

Різні варіантирозташування п людина в черзі відрізняються один від одного тільки порядком розташування людей, тобто є різними перестановками з п елементів.

Три людини можуть стати в чергу Р3 = 3! = 6 у різний спосіб.

Відповідь: 1) 6 способів; 2) 120 методів.

2. Т. Скільки способами 4 людини можуть розміститися на чотиримісній лаві?

Рішення.

Кількість осіб дорівнює кількості місць на лавці, тому кількість способів розміщення дорівнює кількості перестановок з 4 елементів: Р4 = 4! = 24.

Можна міркувати за правилом твору: для першої людини можна вибрати будь-яке з 4 місць, для другого - будь-яке з 3, для третього - будь-яке з 2, що залишилося, останній займе 1 місце, що залишилося; всього є = 24 різних способів Розміщення 4 осіб на чотиримісній лаві.

Відповідь: 24 способами.

3. М. У Вови на обід - перша, друга, третя страви і тістечко. Він обов'язково почне з тістечка, а все інше з'їсть у довільному порядку. Знайдіть число можливих варіантівобіду.

М-завдання з уч. посібники А.Г.Мордковича

Т-під ред. С.А.Теляковського

Ф-М.В.Ткачовий

Рішення.

Після тістечка Вова може вибрати будь-яку з трьох страв, потім - з двох, і закінчити. Загальна кількість можливих варіантів обіду: =6.

Відповідь: 6.

4. Ф. Скільки різних правильних (з погляду російської) фраз можна скласти, змінюючи порядок слів у реченні: 1) «Я пішов гуляти»; 2) «На подвір'ї гуляє кішка»?

Рішення.

У другому реченні прийменник «во» повинен завжди стояти перед іменником «дворі», до якого він належить. Тому, вважаючи пару «на подвір'ї» за слово, можна знайти кількість різних перестановок трьох умовних слів: Р3 = 3! = 6. Таким чином, і в цьому випадку можна скласти 6 правильних речень.

Відповідь: 1) 6; 2) 6.

5. Скільки можна за допомогою літер К, L, М, Н позначити вершини чотирикутника?

Рішення.

Вважатимемо, що вершини чотирикутника пронумеровані, за кожною закріплений постійний номер. Тоді завдання зводиться до підрахунку числа різних способів розташування 4 літер на 4 місцях (вершинах), тобто до підрахунку різних перестановок: Р4 = 4! =24 методи.

Відповідь: 24 способи.

6. Ф. Чотири друга купили квитки в кіно: на 1-е та 2-е місця у першому ряду та на 1-е та 2-е місця у другому ряду. Скільки способами друзі можуть зайняти ці 4 місця у кінотеатрі?

Рішення.

Чотири друзі можуть зайняти 4 різних місця Р4 = 4! = 24 у різний спосіб.

Відповідь: 24 способи.

7. Т. Кур'єр повинен рознести пакети до 7 різних установ. Скільки маршрутів він може вибрати?

Рішення.

Під маршрутом слід розуміти порядок відвідин кур'єром установ. Пронумеруємо установи номерами від 1 до 7, тоді маршрут буде послідовністю з 7 Цифр, порядок яких може змінюватися. Кількість маршрутів дорівнює кількості перестановок з 7 елементів: Р7 = 7! = 5040.

Відповідь: 5040 маршрутів.

8. Т. Скільки існує виразів, тотожно рівних добутку abcde, які виходять із нього перестановкою множників?

Рішення.

Дано твір п'яти різних співмножників abcde, порядок яких може змінюватись (при перестановці множників твір не змінюється).

Усього існує Р5 = 5! = 120 різних способів розташування п'яти множників; один з них (abcde) вважаємо вихідним, решта 119 виразів тотожно дорівнює цьому.

Відповідь: 119 виразів.

9. Т. Ольга пам'ятає, що телефон подруги закінчується цифрами 5, 7, 8, але забула, в якому порядку ці цифри йдуть. Вкажіть найбільше варіантів, які їй доведеться перебрати, щоб додзвонитися подрузі.

Рішення.

Три останні цифри телефонного номера можуть бути розташовані в одному з Р3 = 3! =6 можливих порядків, у тому числі лише одне правильний. Ольга може одразу набрати правильний варіант, може набрати його третім, і т. д. Найбільше варіантів їй доведеться набрати, якщо правильний варіантвиявиться останнім, тобто шостим.

Відповідь: 6 варіантів.

10. Т. Скільки шестизначних чисел (без повторення цифр) можна становити з цифр: а) 1,2, 5, 6, 7, 8; б) 0, 2, 5, 6, 7, 8? Рішення.

а) Дано 6 цифр: 1, 2, 5, 6, 7, 8, їх можна становити різні шестизначні числа, лише переставляючи ці цифри місцями. Кількість різних шестизначних чисел дорівнює Р6 = 6! = 720.

б) Дано 6 цифр: 0, 2, 5, 6, 7, 8, їх потрібно становити різні шестизначні числа. Відмінність від попередньої завдання у тому, що нуль неспроможна стояти першому місці.

Можна безпосередньо застосувати правило твору: перше місце можна вибрати будь-яку з 5 цифр (крім нуля); на друге місце - будь-яку з 5 цифр, що залишилися (4 «ненульові» і тепер вважаємо нуль); на третє місце - будь-яку з 4 цифр, що залишилися після перших двох виборів, і т. д. Загальна кількість варіантів дорівнює: = 600.

Можна застосувати спосіб виключення зайвих варіантів. 6 цифр можна переставити Р6 = 6! = 720 у різний спосіб. Серед цих способів будуть такі, у яких на першому місці стоїть нуль, що є неприпустимим. Підрахуємо кількість цих неприпустимих варіантів. Якщо першому місці стоїть нуль (він фіксований), то наступних п'яти місцях можуть стояти у довільному порядку «ненульові» цифри 2, 5, 6, 7, 8. Кількість різних способів, якими можна розмістити 5 цифр на 5 місцях, дорівнює Р5 = 5! = 120, т. е. кількість перестановок чисел, що починаються з нуля, дорівнює 120. Потрібна кількість різних шестизначних чисел в цьому випадку дорівнює: Р6 - Р5 = 720 - 120 = 600.

Відповідь: а) 720; б) 600 чисел.

11. Т. Скільки серед чотиризначних чисел(без повторення цифр), складених із цифр 3, 5, 7, 9, таких, які: а) починаються з цифри 3;

б) кратні 15?

Рішення.

а) З цифр 3, 5, 7, 9 складаємо чотиризначні числа, що починаються із цифри 3.

Фіксуємо цифру 3 першому місці; тоді на трьох, що залишилисямісцях у довільному порядку можуть розташовуватися цифри 5, 7 9 Загальна кількість варіантів їх розташування дорівнює Р 3 = 3!=6. Стільки і буде різних чотиризначних чисел, складених ізданих цифр та починаються з цифри 3.

б) Зауважимо, що сума даних цифр 3 + 5 + 7 + 9 = 24 ділиться на 3, отже будь-яке чотиризначне число, складене з цих цифр, ділиться на 3. Для того, щоб деякі з цих чисел ділилися на 15, необхідно, щоб вони закінчувалися цифрою 5.

Фіксуємо цифру 5 на останньому місці; решту 3 цифр можна розмістити на трьох місцях перед 5 Рз = 3! = 6 у різний спосіб. Стільки і буде різних чотиризначних чисел, складених із даних цифр, які поділяються на 15.

Відповідь: а) 6 чисел; б) 6 чисел.

12. Т. Знайдіть суму цифр усіх чотиризначних чисел, які можна становити із цифр 1, 3, 5, 7 (без їх повторення).

Рішення.

Кожне чотиризначне число, складене із цифр 1, 3, 5, 7 (без повторення), має суму цифр, що дорівнює 1+3 + 5 + 7=16.

З цих цифр можна становити Р4 = 4! = 24 різних числа, що відрізняються лише порядком цифр. Сума цифр усіх цих чисел дорівнюватиме

16 = 384.

Відповідь: 384.

13. Т. Сім хлопчиків, до яких входять Олег та Ігор, стають у ряд. Знайдіть число можливих комбінацій, якщо:

а) Олег повинен перебувати наприкінці ряду;

б) Олег повинен перебувати на початку ряду, а Ігор – наприкінці ряду;

в) Олег та Ігор мають стояти поруч.
Рішення.

а) Усього 7 хлопчиків на 7 місцях, але один елемент фіксований, не переставляється (Олег знаходиться в кінці ряду). Число можливих комбінацій у своїй дорівнює числу перестановок 6 хлопчиків, які стоять перед Олегом: Р6=6!=720.

пару як єдиний елемент, що переставляється з іншими п'ятьма елементами. Число можливих комбінацій тоді буде Р6 = 6! = 720.

Нехай тепер Олег та Ігор стоять поруч у порядку ІВ. Тоді отримаємо ще Р6 = 6! = 720 інших комбінацій.

Загальна кількість комбінацій, у яких Олег та Ігор стоять поруч (у будь-якому порядку) дорівнює 720 + 720 = 1440.

Відповідь: а) 720; б) 120; в) 1440 комбінацій.

14. М. Одинадцять футболістів будуються перед початком матчу. Першим стає капітан, другим - воротар, інші - випадковим чином. Скільки існує способів побудови?

Рішення.

Після капітана і воротаря третій гравець може вибрати будь-яке з 9 місць, наступний - з 8, і т. д. Загальна кількість способів побудови за правилом твору дорівнює:

1 = 362880, або Р 9 = 9! = 362880.

Відповідь: 362 880.

15. М. Скільки способами можна позначити вершини куба літерами А, В, С, D, E, F, G, K?

Рішення.

Для першої вершини можна вибрати будь-яку з 8 букв, для другої - будь-яку з 7, що залишилися, і т. д. Загальна кількість способів за правилом твору дорівнює= 40320, або Р8 = 8!

Відповідь: 40 320.

16. Т. У розкладі на понеділок шість уроків: алгебра, геометрія, біологія, історія, фізкультура, хімія. Скільки способами можна скласти розклад уроків цього дня так, щоб два уроки математики стояли поруч?

Рішення.

Усього 6 уроків, їх два уроки математики повинні стояти поруч.

«Склеюємо» два елементи (алгебра та геометрія) спочатку в порядку АГ, потім у порядку ГА. При кожному варіанті "склеювання" отримуємо Р5 = 5! = 120 варіантів розкладу. Загальна кількість способів скласти розклад дорівнює 120(AГ) +120(ГА) = 240.

Відповідь: 240 способів.

17. Т. Скільки існує перестановок літер слова «конус», у яких літери К, Про, Н стоять поруч?

Рішення.

Дано 5 букв, у тому числі три букви повинні стояти поруч. Три літери К, Про, Н можуть стояти поруч із Р3 = 3! = 6 методів. Для кожного способу "склеювання" літер К, О, Н отримуємо Р3 = 3! = 6 способів перестановки букв, «склейка», У, З. Загальна кількість різних перестановок букв слова «конус», у яких букви До, Про, Н стоять поруч, дорівнює 6 6 = 36 перестановок- анаграм.

Відповідь: 36 анаграм.

18. Т. Скільки способами 5 хлопчиків та 5 дівчаток можуть зайняти в театрі в одному ряду місця з 1 по 10? Скільки способами вони можуть це зробити, якщо хлопчики сидітимуть на непарних місцях, а дівчатка – на парних?

Рішення.

Кожен варіант розташування хлопчиків може поєднуватися з кожним варіантом розташування дівчаток, тому за правилом твору загальне числоспособів розсадити дітей у цьому випадку дорівнює 120 20= 14400.

Відповідь: 3628800 способів; 14400 способів.

19. Т. П'ять хлопчиків і чотири дівчинки хочуть сісти на лавку дев'ятимісцеву так, щоб кожна дівчинка сиділа між двома хлопчиками. Скільки вони можуть це зробити?

Рішення.

За умовою завдання хлопчики і дівчатка повинні чергуватись, тобто дівчатка можуть сидіти тільки на парних місцях, а хлопчики лише на непарних. Тому змінюватися місцями дівчинки можуть лише з дівчатками, а хлопчики – лише з хлопчиками. Чотирьох дівчаток можна розсадити на чотирьох парних місцях Р4 = 4! = 24 способами, а п'ятьох хлопчиків на п'яти непарних місцях Р5 = 5! = 120 методами.

Кожен спосіб розміщення дівчаток може поєднуватися з кожним способом розміщення хлопчиків, тому за правилом твору загальна кількість способів дорівнює Р420 = 2880 способів.

Відповідь: 2880 способів.

20. Ф. Розкласти на прості множники числа 30 та 210. Скількими способами можна записати у вигляді добутку продих множників число: 1) 30; 2) 210?

Рішення.

Розкладемо дані числа на прості множники:

30 = 2 ; 210 = 2 .

Число 30 можна записати у вигляді добутку простих множників

Р 3 = 3! = 6 різними способами(переставляючи множники).

Число 210 можна записати у вигляді твору простих
множниківР 4 = 4! = 24 різними способами.

Відповідь: 1) 6 способів; 2) 24 способи.

21. Ф. Скільки різних парних чотиризначних чисел з цифрами, що не повторюються, можна записати, використовуючи цифри 1, 2, 3, 5?

Рішення.

Щоб число було парним, воно має закінчуватися парною цифрою, тобто 2. Зафіксуємо двійку на останньому місці, решта трьох цифр має стояти перед нею в довільному порядку. Кількість різних перестановок із 3 цифр дорівнює P3 = 3! = 6; отже, різних парних чотиризначних чисел буде також 6 (до кожної перестановки із трьох цифр додається цифра 2).

Відповідь: 6 чисел.

22. Ф. Скільки різних непарних п'ятицифрових чисел, у яких немає однакових цифр, можна записати за допомогою Цифр 1,2, 4, 6, 8?

Рішення.

Щоб складене число було непарним, необхідно, щоб воно закінчувалося непарною цифрою, тобто одиницею. Інші 4 Цифри можна переставляти місцями, розташовуючи кожну перестановку перед одиницею.

Загальна кількість непарних п'ятизначних чисел дорівнює числу перестановок: Р4 = 4! =24.

23. Ф. Скільки різних шестизначних чисел з цифрами, що не повторюються, можна записати за допомогою цифр 1; 2 3, 4, 5, 6, якщо: 1) число повинне починатися з 56; 2) цифри 5 і 6 у числі мають стояти поряд?

Рішення.

Дві цифри 5 і 6 фіксуємо на початку числа і дописуємо до них різні перестановки з 4 цифр, що залишилися; кількість різних шестицифрових чисел дорівнює: Р4 = 4! = 24.

Загальна кількість різних шестизначних чисел, у яких цифри 5 та 6 стоять поруч (у будь-якому порядку), дорівнює 120 + 120 = 240 чисел. (Варіанти 56 та 65 несумісні, не можуть реалізуватися одночасно; застосовуємо комбінаторне правило суми.)

Відповідь: 1) 24 числа; 2) 240 чисел.

24. Ф. Скільки різних парних чотиризначних чисел, у запису яких немає однакових цифр, можна скласти із цифр 1,2,3,4?

Рішення.

Парне число повинне закінчуватися парною цифрою. Фіксуємо на останньому місці цифру 2, тоді попередні 3 цифри можна переставити Р3 = 3! = 6 у різний спосіб; отримаємо 6 чисел із двійкою на кінці. Фіксуємо на останньому місці цифру 4, отримаємо Р3 = 3! = 6 різних перестановок трьох попередніх цифр та 6 чисел, що закінчуються цифрою 4.

Загальна кількість парних чотирицифрових чисел буде 6 + 6 = 12 різних чисел.

Відповідь: 12 чисел.

Зауваження. Загальна кількість варіантів ми знаходимо, користуючись комбінаторним правилом суми (6 варіантів чисел, що закінчуються двійкою, 6 варіантів чисел, що закінчуються четвіркою; способи побудови чисел з двійкою та з четвіркою на кінці є взаємовиключними, несумісними, тому Загальна кількістьваріантів дорівнює сумі числа варіантів із двійкою на кінці та числа варіантів із 4 на кінці). Запис 6 + 6 = 12 краще відображає основи наших дій, ніж запис Р.

25. Ф. Скільки способами можна записати у вигляді добутку простих множників число 1) 12; 2) 24; 3) 120?

Рішення.

Особливістю цього завдання є те, що в розкладанні кожного з даних чисел є однакові множники, що повторюються. При освіті різних перестановок з множників ми отримаємо нову перестановку, якщо поміняємо місцями якісь два однакових множника.

1) Число 12 розкладається на три простих множники, два з яких однакові: 12 = .

Якби всі множники були різні, їх можна було б переставити у творі Р3 = 3! = 6 у різний спосіб. Щоб перерахувати ці способи, умовно «розрізнимо» дві двійки, підкреслимо одну з них: 12 = 2.

Тоді можливі такі 6 варіантів розкладання на мешканці:

Але насправді підкреслення цифр не має в математиці жодного значення, тому отримані 6 перестановок у звичайному записі мають вигляд:

т. е. фактично ми отримали не 6, а 3 різні перестановки Кількість перестановок зменшилася вдвічі за рахунок того, що ми не повинні враховувати перестановки двох двійок між собою.

Позначимо Р х шукане число перестановок із трьох елементів серед яких два однакових; тоді отриманий нами результат можна записати так: Рз = Рх Але 2 - це кількість різних перестановок із двох елементів, тобто 2 == 2! = Р 2 тому Р3, = Р х Р 2 , звідси Р х = . (Це формула для числа перестановок із повтореннями).

Можна міркувати інакше, ґрунтуючись лише на комбінаторному правилі твору.

Щоб скласти твір із трьох множників, спочатку виберемо місце для множника 3; це можна зробити одним із трьох способів. Після цього обидва місця заповнюємо двійками; це можна зробити одним способом. За правилом твору загальна кількість методів дорівнює: 3-1 =3., Р х = 20.

Другий спосіб. Складаючи твір з п'яти множників, спочатку виберемо місце для п'ятірки (5 способів), потім для трійки (4 способи), а 3 місця, що залишилися, заповнимо двійками (1 спосіб); за правилом твору 5 4 1 = 20.

Відповідь: 1) 3; 2) 4; 3) 20.

26. Ф. Скільки способами можна зафарбувати 6 клітин таким чином, щоб 3 клітини були червоними, а 3 залишилися зафарбовані (кожна своїм кольором) білим, чорним чи зеленим?

Рішення.

Перестановки із 6 елементів, серед яких три - однакові:

Інакше: для зафарбування білим кольором можна вибрати одну з 6 клітин, чорним – з 5, зеленим – з 4; три клітини, що залишилися, зафарбовуємо червоним кольором. Загальна кількість способів: 6541 = 120.

Відповідь: 120 способів.

27.Т. Пішохід має пройти один квартал на північ та три квартали на захід. Випишіть усі можливі маршрути пішохода.= 4.

Відповідь: 4 маршрути.

28. М. а) На дверях чотирьох однакових кабінетів треба повісити таблички із прізвищами чотирьох заступників директора. Скільки способами це можна зробити?

б) У 9 «А» класі у середу 5 уроків: алгебра, геометрія, фізкультура, російська мова, англійська мова. Скільки можна скласти варіантів розкладу на цей день?

в) Скільки способами чотири злодії можуть розбігтися по одному на всі чотири сторони?

г) Ад'ютант повинен розвезти п'ять копій наказу генерала до п'яти полків. Скільки способів може вибрати маршрут доставки копій наказу?

Рішення.

а) Для першої таблички можна вибрати будь-який із 4 кабінетів,
Для другої - будь-який з трьох решти, для третьої - будь-який з двох решти, для четвертої - один решта; за правилом
твори загальна кількість способів дорівнює: 4 3 2 1 = 24, або Р4 = 4! = 24.= 120, або Р5 = 5! = 120.

Відповідь: а) 24; б) 120; в) 24; г) 120.

Література

Афанасьєв В.В. Теорія ймовірностей у прикладах та завданнях, - Ярославль: ЯГПУ, 1994.

Баврін І. І. Вища математика: Підручник для студентів хіміко-математичних спеціальностей педагогічних вузів-2-е видання, перероблене. - М.: Просвітництво, 1993.

Бунимович Є. А., Буличов В.А. Імовірність та статистика. 5-9 класи: Посібник для загальноосвітніх навчальних закладів, - М.: Дроф, 2005.

Віленкін Н. Я. та інші. Алгебра та математичний аналіздля 10 класу: Навчальний посібникдля учнів шкіл та класів з поглибленим вивченнямматематики. - М: Просвітництво,1992.

Віленкін Н. Я. та інші. Алгебра та математичний аналіз для 11 класу: Навчальний посібник для учнів шкіл та класів з поглибленим вивченням математики - М.: Просвітництво, 1990.

Глейзер Г.І. Історія математики у школі: 9-10 клас. Посібник для вчителів. - М: Просвітництво 1983.

Дорофєєв Г.В., Суворова С.Б., Бунімович Є.А. Математика 9: Алгебра. Опції. Аналіз даних – М.: Дрофа, 2000.

Колягін та інші. Алгебра та початку аналізу 11 клас. Математика у школі – 2002 - №4 – с.43,44,46.

Люпшкас В.С. Факультативні курси з математики: теорія ймовірностей: Навчальний посібник для 9-11 класів. - М., 1991.

Макарічев Ю.М., Міндюк Н.Г. Елементи статистики та теорії ймовірностей: Навчальний посібник для учнів 7-9 класів. - М.: Просвітництво, 2005.

Мордковіч А.Г., Семенов П.В. Алгебра та початку аналізу 10 клас: Підручник для загальноосвітніх установ (профільний рівень) - М.: Мнемозіна, 2005.

Ткачова М.В., Федорова Н.Є. Елементи статистики та ймовірність: Навчальний посібник для учнів 7-9 класів. - М.: Просвітництво, 2005.

У комбінаториці вивчають питання, скільки комбінацій певного типу можна скласти з даних предметів (елементів).

Народження комбінаторики як розділу математики пов'язане з працями Б. Паскаля та П. Ферма з теорії азартних ігор. Великий внесок у розвиток комбінаторних методів зробили Г.В. Лейбніц, Я. Бернуллі та Л. Ейлер.

Французький філософ, письменник, математик та фізик Блез Паскаль (1623–1662) рано виявив свої видатні математичні здібності. Коло математичних інтересів Паскаля було дуже різноманітне. Паскаль довів одну з основних теорем проективної геометрії (теорема Паскаля), сконструював підсумовуючу машину (арифмометр Паскаля), дав спосіб обчислення біноміальних коефіцієнтів (трикутник Паскаля), вперше точно визначив і застосував для доказу метод математичної індукції, зробив суттєвий крок у розвитку , зіграв важливу рольу зародженні теорії ймовірності. У гідростатиці Паскаль встановив її основний закон (закон Паскаля). "Листи до провінціалу" Паскаля з'явилися шедевром французької класичної прози.

Готфрід Вільгельм Лейбніц (1646–1716) – німецький філософ, математик, фізик та винахідник, юрист, історик, мовознавець. У математиці поруч із І. Ньютоном розробив диференціальне та інтегральне числення. Важливий внесок зробив комбінаторику. З його ім'ям, зокрема, пов'язані теоретико-числові задачі.

Готфрід Вільгельм Лейбніц мав мало значну зовнішність і тому справляв враження досить непоказної людини. Одного разу в Парижі він зайшов у книжкову крамницю, сподіваючись придбати книгу свого знайомого філософа. На запитання відвідувача про цю книгу книготорговець, оглянувши його з голови до ніг, насмішкувато кинув: “Навіщо вона вам? Невже ви здатні читати такі книги? Не встиг вчений відповісти, як до крамниці увійшов сам автор книги зі словами: "Великому Лейбницю привіт та повага!" Продавець ніяк не міг зрозуміти, що перед ним справді знаменитий Лейбніц, книги якого мали великий попит серед учених.

Надалі важливу роль гратиме наступна

Лемма.Нехай у множині елементів, а в множині-елементів. Тоді число всіх різних пар, де буде рівним.

Доведення.Дійсно, з одним елементом з безлічі ми можемо скласти таких різних пар, а всього в безлічі елементів.

Розміщення, перестановки, поєднання

Нехай у нас є безліч із трьох елементів. Якими способами ми можемо вибрати з цих елементів два?

Визначення.Розміщеннями множини з різних елементів поелементів називаються комбінації, які складені з даних елементів поелементів і відрізняються або самими елементами, або порядком елементів.

Число всіх розміщень множини з елементів поелементів позначається через (від початкової літери французького слова "arrangement", що означає розміщення), деі.

Теорема.Число розміщень безлічі з елементів поелементів дорівнює

Доведення.Нехай у нас є елементи. Нехай-можливі розміщення. Будуватимемо ці розміщення послідовно. Спочатку визначимо-перший елемент розміщення. З цієї сукупності елементів його можна вибрати різними способами. Після вибору першого елемента для другого елемента залишається способів вибору і т.д. Оскільки кожен такий вибір дає нове розміщення, всі ці вибори можна вільно комбінувати між собою. Тому маємо:

приклад.Скільки способами можна скласти прапор, що складається з трьох горизонтальних смуг різних кольорів, якщо є матеріал п'яти кольорів?

Рішення.Потрібна кількість трисмугових прапорів:

Визначення.Перестановкою множини з елементів називається розташування елементів у певному порядку.

Так, всі різні перестановки множини з трьох елементів - це

Число всіх перестановок з елементів позначається (від початкової літери французького слова "permutation", що означає "перестановка", "переміщення"). Отже, число всіх різних перестановок обчислюється за формулою

приклад.Скільки способами можна розставити 8 тур на шахівниці так, щоб вони не били один одного?

Завдання . Визначити кількість усіх упорядкованих наборів довжини r, які можна скласти з елементів множини X (
), якщо вибір кожного елемента
, Виробляється з усього безлічі X.

Упорядкований набір
– це елемент декартового твору
, що складається з rоднакових множників X. За правилом твору кількість елементів множини
одно
. Ми вивели формулу
.

приклад. Скільки чотиризначних номерів можна скласти, якщо використовувати всі десять цифр?

Тут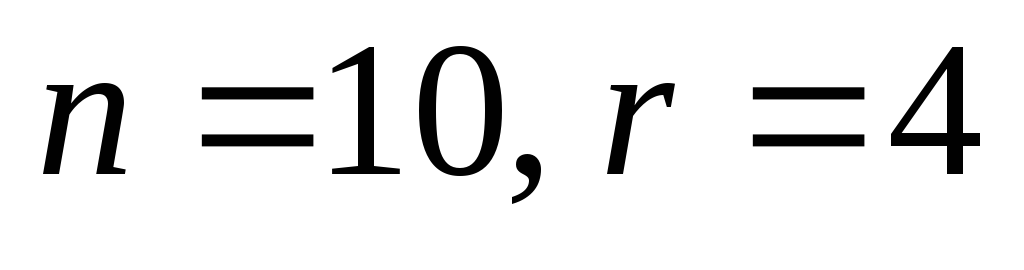
, і кількість телефонних номеріводно

2.1.5. Розміщення без повторень

Завдання . Скільки впорядкованих наборів
можна скласти з nелементів множини Xякщо всі елементи набору різні?

Перший елемент можна вибрати nметодами. Якщо перший елемент уже вибраний, другий елемент можна вибрати лише
способами, а якщо вже обраний
елемент
, то елемент можна вибрати
способами (повторення обраного елемента заборонена). За правилом твору отримуємо

Ця формула записується інакше з використанням позначення
. Так як

.

приклад. Скільки може бути різних списків переможців олімпіади (перше, друге, третє місце), якщо брало участь 20 людина?

Тут
, шуканим є число

2.1.6. Перестановки без повторень

Розглянемо окремий випадок розміщення без повторень: якщо
, то в розміщенні беруть участь усі елементи множини X, тобто. Вибірки мають однаковий склад і відрізняються один від одного лише порядком елементів. Такі вибірки називаються перестановками . Кількість перестановок з nелементів позначають :

приклад.Скільки способами можна вишикувати чергу до каси, якщо хочуть отримати зарплату шість осіб?

2.1.7. Перестановки із повтореннями

Нехай безліч Xскладається з kрізних елементів:
.Перестановкою із повтореннями складу
будемо називати впорядкований набір довжини
, в якому елемент зустрічається раз
. Кількість таких перестановок позначається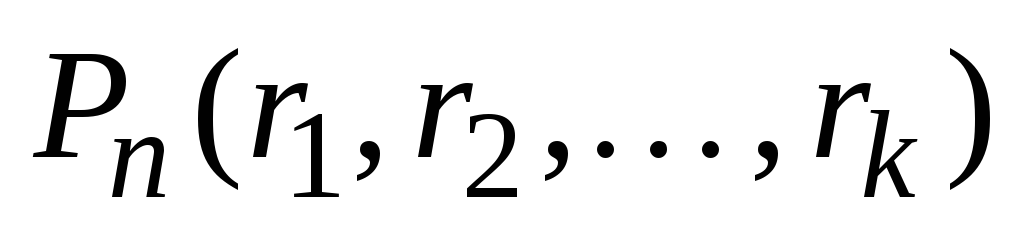
.

приклад. З літер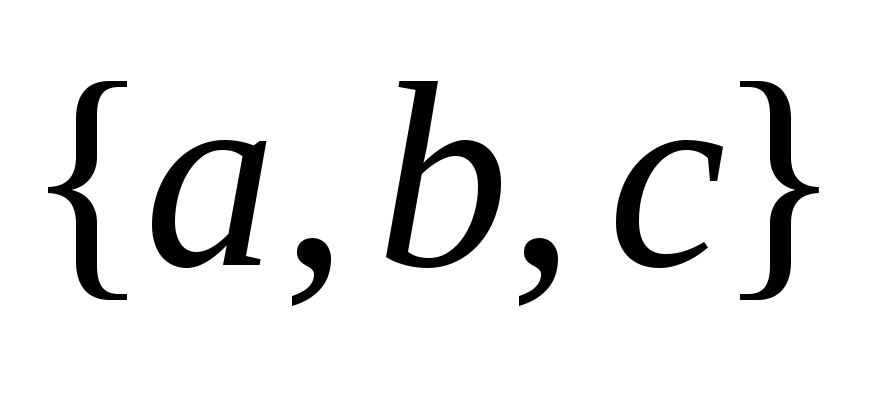
запишемо перестановку з повторенням складу
. Її довжина
, причому буква aвходить 2 рази, b- 2 рази, c- один раз. Такою перестановкою буде, наприклад,
або
.

Виведемо формулу кількості перестановок із повтореннями. Занумеруємо всі однакові елементи, які входять у перестановку, різними індексами, тобто. замість перестановки
отримаємо
. Тепер всі елементи перестановки різні, а кількість таких перестановок дорівнює
. Перший елемент зустрічається у вибірці разів. Приберемо індекси у першого елемента (у нашому прикладі отримаємо перестановку
), при цьому кількість різних перестановок зменшиться в 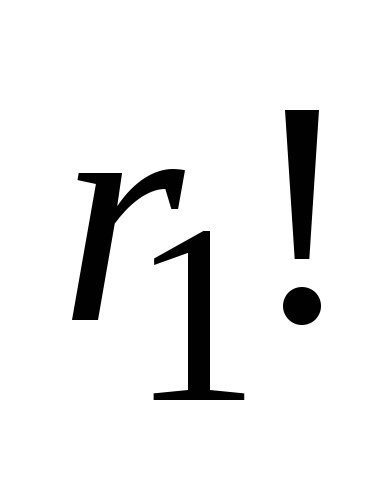разів, т.к. при зміні порядку однакових елементів наша вибірка не зміниться. Приберемо індекси у другого елемента – кількість перестановок зменшиться у разів. І так далі, до елемента з номером k- Число перестановок зменшиться в разів. Отримаємо формулу

приклад. Скільки різних "слів" можна отримати, переставляючи букви слова "передача"?

У цьому слові літери "е" і "а" зустрічаються двічі, решта по одному разу. Йдеться про перестановку із повторенням складу
довжини. Кількість таких перестановок дорівнює

2.1.8. Поєднання

Завдання . Скільки різних множин з rелементів можна скласти з множини, що містить nелементів?

Складатимемо спочатку впорядковані набори по rелементів у кожному. Кількість таких наборів (це розміщення з nелементів по r) одно
. Тепер враховуємо, що порядок запису елементів нам байдужий. При цьому з різних розміщень, що відрізняються лише порядком елементів, отримаємо одне поєднання. Наприклад, два різних розміщення
і
з двох елементів відповідають одному поєднанню
. Таким чином, кількість поєднань в 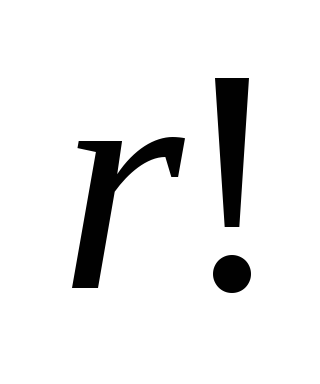раз менше числарозміщень :

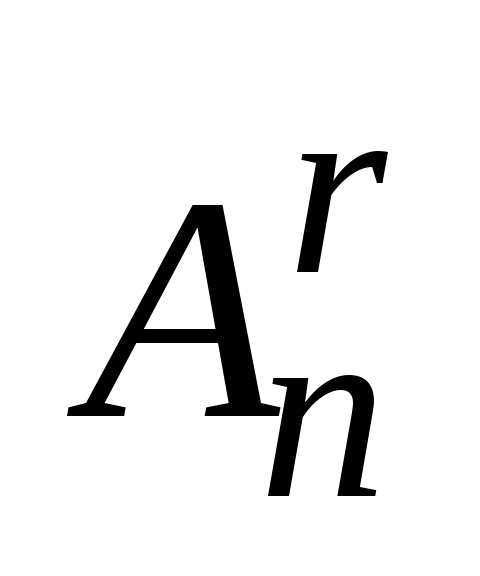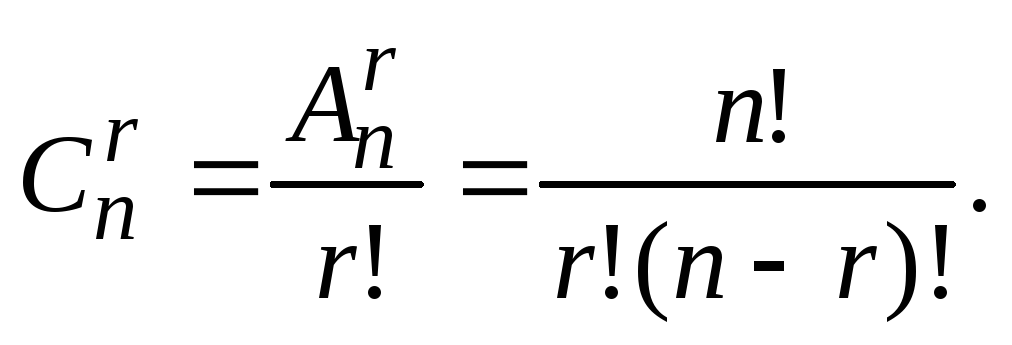
приклад. Кількість способів, якими ми можемо вибрати з восьми двірників трьох, дорівнює

Комбінаторика - Розділ математики, в якому вивчаються питання про те, скільки різних комбінацій, підпорядкованих тим чи іншим умовам, можна скласти із заданих об'єктів.

Комбінаторика виникла XVI столітті. Перші комбінаторні завдання стосувалися азартних ігор. Сьогодні комбінаторні методи використовуються для вирішення транспортних завдань, складання планів виробництва та реалізації продукції. Встановлено зв'язки між комбінаторикою та завданнями лінійного програмуваннястатистики. Комбінаторика використовується для складання та декодування шифрів, для вирішення інших проблем теорії інформації.

Значну роль комбінаторні методи грають і в суто математичних питаннях - теорії груп та їх уявлень, вивченні основ геометрії, неасоціативних алгебр та ін.

Приклад комбінаторного завдання. Скільки трицифрових чиселможна скласти із цифр 0, 2, 4, 6, 8, використовуючи в записі числа кожну з них не більше одного разу?

IМетод. Намагатимемося виписати всі такі числа. На першому місці може стояти будь-яка цифра крім 0. Наприклад, 2. На другому місці будь-яка цифра з 0, 4, 6 і 8. Нехай 0. Тоді як третю цифру можна вибрати будь-яку з 4, 6, 8. Отримуємо три числа

Замість 0 на друге місце можна було поставити 4, тоді третє цифрою можна записати або 0 або 6, або 8:

Розмірковуючи аналогічно, отримуємо ще дві трійки тризначних чисел із цифрою 2 на першому місці:

Інших, окрім виписаних 12-ти, тризначних чисел із цифрою 2 на першому місці, і задовольняють умові, немає.

Якщо на першому місці записати цифру 4, а решту вибирати із цифр 0, 2, 6, 8, то отримаємо ще 12 чисел:

По стільки тризначних чисел можна скласти з цифрою 6 на першому місці і цифрою 8 на першому місці. Отже, потрібна кількість:

Ось ці числа:

204, 206, 208, 240, 246, 248, 260, 264, 268, 280, 284, 286;

402, 406, 408, 420, 426, 428, 460, 462, 468, 480, 482, 486;

602, 604, 608, 620, 624, 628, 640, 642, 648, 680, 682, 684;

802, 804, 806, 820, 824, 826, 840, 842, 846, 860, 862, 864.

Відповідь: 48. ◄

Метод міркування, яким ми скористалися під час вирішення попереднього завдання, називається перебором можливих варіантів .

Правила складання та множення

Комбінаторне правило додавання(правило "або") — одне з основних правил комбінаторики, яке стверджує, що якщо є n елементів та елемент A 1можна вибрати m 1 способами, елемент A 2можна вибрати m 2 A n можна вибрати m n способами, то вибрати або A 1, або A 2, або, і так далі, A n можна, можливо

m 1 + m 2 + ... + m n

методами.

Наприклад, вибрати подарунок дитині з 9 машинок, 7 плюшевих ведмедів та 3 залізницьможна, можливо

методами.

Відповідь: 19. ◄

Правило множення (правило "і") - Ще одне з важливих правилкомбінаторики. Згідно з ним, якщо елемент A 1можна вибрати m 1 способами, елемент A 2можна вибрати m 2 способами і так далі, елемент A n можна вибрати m n способами, то набір елементів ( A 1, A 2, ... , A n ) можна вибрати

m 1 · m 2 · ... · m n

методами.

Наприклад.

1) Вибрати дитині в подарунок машинку, плюшевого ведмедя та залізницю, вибираючи з 9 машинок, 7 плюшевих ведмедів та 3 залізниць, можна

9 · 7 · 3 = 189

методами.

Відповідь: 189.

2) Скористаємося правилом множення для розв'язання задачі, вже розглянутої вище: Скільки трицифрових чисел можна становити з цифр 0, 2, 4, 6, 8, використовуючи в записі числа кожну з них не більше одного разу?

IIМетод.

0 не може стояти першим, значить першу цифру потрібно вибрати з 2, 4, 6, 8 - 4 способи;

другою цифрою може бути будь-яка з чотирьох, що залишилися - 4 способи;

третю цифру можна вибрати серед трьох решти - 3 способи.

Отже, кількість тризначних чисел, що шукається:

4 · 4 · 3 = 48.

Відповідь: 48. ◄

Перестановки

Безліч із n елементів називається упорядкованим якщо кожному його елементу поставлено у відповідність натуральне число від 1 до n .

Перестановкою з n елементів називається будь-яке впорядковане безліч з n елементів.

Наприклад, із 4 елементів ♦ ♣ ♠ можна скласти наступні 24 перестановки:

♦ ♣ ♠	♦ ♣ ♠	♣ ♦ ♠	♠ ♦ ♣
♦ ♠ ♣	♦ ♠ ♣	♣ ♦ ♠	♠ ♦ ♣
♦ ♣ ♠	♣ ♦ ♠	♣ ♦ ♠	♠ ♦ ♣
♦ ♣ ♠	♣ ♠ ♦	♣ ♠ ♦	♠ ♣ ♦
♦ ♠ ♣	♠ ♦ ♣	♣ ♠ ♦	♠ ♣ ♦
♦ ♠ ♣	♠ ♣ ♦	♣ ♠ ♦	♠ ♣ ♦

◄

Кількість перестановок з n елементів прийнято позначати P n . За допомогою перебору можливих варіантів легко переконатися, що

P 1 = 1; P 2 = 2; P 3 = 6; P 4 = 24.

Взагалі, кількість різноманітних перестановок з n елементів дорівнює добутку всіх натуральних чиселвід 1 до n , тобто n! (читається "ен факторіал"):

P n= 1 · 2 · 3 · ... · ( n - 1 ) · n = n!.

Для P nсправедлива рекурентна формула:

P n = n· P n - 1 .

Значення факторіалу визначено не тільки для натуральних чисел, а й для 0:

0! = 1 .

Таблиця факторіалів цілих чисел від 0 до 10
n		1	2	3	4	5	6	7	8	9	10
n!	1	1	2	6	24	120	720	5 040	40 320	362 880	3 628 800

Наприклад, скільки способів 5 хлопчиків і 5 дівчаток можуть зайняти в театрі місця в одному ряду з 1-го по 10-е місце, якщо жодні два хлопчики і жодні дві дівчинки не сидять поруч?

Можливі два випадки з однаковою кількістю способів: 1) хлопчики – на непарних місцях, дівчатка на парних та 2) навпаки.

Розглянемо перший випадок. Хлопчики по непарних місцях можуть сісти

P 5 = 120

методами. Стільки способів для дівчаток на парних місцях. Згідно з правилом множення, хлопчики — на непарних місцях, дівчатка на парних можуть розташуватися

120 · 120 = 14400

методами. Значить, всього способів

14 400 + 14 400 = 28 800.

Відповідь: 28 800. ◄

Перестановки із повтореннями

Перестановкою із повтореннями з n елементів, серед яких k різних, при цьому налічується n 1 невиразних елементів першого типу, n 2 невиразних елементів другого типу і так далі, n k невиразних елементів k -го типу (де n 1 + n 2 + … + n k = n ), називається будь-яке розташування цих елементів по n різних місць.

Число перестановок із повтореннями довжини n з k різних елементів, взятих відповідно до n 1 , n 2 , …, n k раз кожен позначається і обчислюється так: $$ P_(n_1,n_2, ... , n_k)=\frac(n{n_1!n_2! ... n_k!}~.$$!}

Наприклад, скільки різних десятизначних чисел можна становити з цифр: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4?

У даному випадку: n = 10, n 1 = 1, n 2 = 2, n 3 = 3, n 4 = 4,$$P_(1, 2, 3, 4)=\frac(10{1!2! 3! 4!}=\frac{10!}{1!2! 3! 4!}=12~600.$$!}

Відповідь: 12 600. ◄

Розміщення

Розміщенням з n елементів m(m ≤ n) m елементів, взятих у визначеному порядку з даних n елементів.

Два розміщення з nелементів по mвважаються різними, якщо вони відрізняються самими елементами чи порядком їхнього розташування.

Наприклад, складемо всі розміщення з чотирьох елементів A, B, C, Dпо два елементи:

A B; A C; A D;

B A; B C; B D;

C A; C; C D;

D A; D; DC.

◄

Число всіх розміщень з nелементів по mпозначають \(A_n^m\) (читається: " Аз nпо m") і обчислюється за будь-якою з формул:$$A_n^m=n\cdot (n-1)\cdot (n-2)\cdot ...\cdot (n-m+1)\\A_n^m= \frac(n{(n-m)!}$$!}

Приклади завдань.

1) Скористаємося поняттям розміщень з n елементів по m для розв'язання задачі, що вже двічі розглянута раніше: Скільки трицифрових чисел можна становити з цифр 0, 2, 4, 6, 8, використовуючи в записі числа кожну з них не більше одного разу?

I IIМетод.

Першу цифру можна вибрати чотирма способами з набору 2, 4, 6, 8. У кожному з цих випадків кількість пар другої та третьої цифри дорівнює кількості розміщень з 4 цифр, що залишилися по 2. Значить кількість тризначних чисел, що шукається, дорівнює: 2=4\cdot \frac(4{(4-2)!}=4\cdot \frac{4!}{2!}=4\cdot (3\cdot 4)=48.$$Ответ: 48.!}

2) Для польоту в космос необхідно укомплектувати екіпаж із шести осіб. До нього повинні входити: командир корабля, перший і другий його помічники, два бортінженери, один з яких старший, і один лікар. Командний склад вибирається з 20 льотчиків, бортінженери — із 15 фахівців, а лікар — із 5 медиків. Скільки способами можна укомплектувати екіпаж?

Оскільки у виборі командного складу важливий порядок, то командира і його помічників можна вибрати \(A_(20)^3\) способами. Порядок бортінженерів теж важливий, отже, їх вибору існує \(A_(15)^2\) способів. Лікар лише один, для його вибору існує 5 методів. Скористаємося комбінаторним правилом множення і знайдемо кількість можливих екіпажів корабля:$$A_(20)^3\cdot A_(15)^2\cdot 5=\frac(20{17!}\cdot \frac{15!}{13!}\cdot 5=(18\cdot 19\cdot 20)\cdot (14\cdot 15)\cdot 5=7~182~000.$$Ответ: 7 182 000. !} ◄

Зрозуміло, що якщо m = n , то$$A_n^m=A_n^n=P_n=n!.$$

Справедливо також, що якщо m = n - 1 , то$$A_n^(n-1)=A_n^n=P_n=n!.$$

Розміщення з повтореннями

Крім звичайних розміщень бувають і розміщення з повтореннями або вибірки із поверненням .

Нехай є n різних об'єктів. Виберемо з них m штук, діючи по наступного принципу. Візьмемо будь-який, але не будемо його встановлювати в якийсь ряд, а просто запишемо під номером 1 його назву, сам об'єкт після цього повернемо до інших. Потім знову з усіх n об'єктів оберемо один (у тому числі, можливо, і той, який був щойно взятий), запишемо його назву, позначивши номером 2, і знову повернемо об'єкт назад. І так далі, поки не отримаємо m назв.

Розміщення з повтореннями позначаються \(\overline(A)_n^m\) і, згідно з правилом множення, обчислюються за формулою $$\overline(A)_n^m=n^m.$$Зауважимо, що тут припустимо випадок, коли m > n тобто обраних об'єктів більше, ніж їх всього є. Це не дивно: кожен об'єкт після "використання" повертається і може бути використаний повторно.

Наприклад, кількість варіантів шестизначного пароля, в якому кожен знак є цифрою від 0 до 9 або літерою латинського алфавіту (одна і та ж мала та велика буква — один символ) і може повторюватися, так само:$$\overline(A)_(10 +26)^6=\overline(A)_(36)^6=36^6=2~176~782~336.$$Якщо ж малі і прописні літеривважаються різними символами (як це зазвичай і буває), кількість можливих паролів стає ще більш колосальним:$$\overline(A)_(10+26+26)^6=\overline(A)_(62)^6= 62^6=56~800~235~584.$$

◄

Поєднання

Поєднанням з n елементів m(m ≤ n) називається будь-яка безліч, що складається з m елементів, вибраних із даних n елементів.

На відміну від розміщень у поєднаннях немає значення, у порядку зазначені елементи. Два поєднання з nелементів по mвважаються різними, якщо вони відрізняються хоча б одним елементом.

Наприклад, складемо всі поєднання із чотирьох елементів A, B, C, Dпо два елементи:

A B; A C; A D;

B C; B D;

C D.

◄

Число всіх поєднань з nелементів по mпозначають \(C_n^m\) (читається: " Cз nпо m") і обчислюється за будь-якою з формул: )~\cdot~ ...~\cdot~ (n-m+1))(1\cdot2\cdot3~\cdot~...~\cdot ~m)$$$$C_n^m=\frac( n{m!\cdot (n-m)!}.$$!}

Приклади завдань.

1) Бригада, що займається ремонтом школи, складається з 12 малярів та 5 теслярів. З них для ремонту фізкультурного залу треба виділити 4 малярів та 2 теслярів. Скільки можна це зробити?

Так як порядок малярів у кожній обраній четвірці і порядок теслярів у кожній обраній парі не має значення, то, згідно з комбінаторним правилом множення, кількість способів, що шукається, дорівнює:$$C_(12)^4 \cdot C_5^2 =\frac(12{4!\cdot 8!}\cdot \frac{5!}{2!\cdot 3!}=\frac{9\cdot10\cdot11\cdot12}{1\cdot2\cdot3\cdot4}\cdot \frac{4\cdot5}{1\cdot 2}=4~950.$$Ответ: 4 950. !} ◄

2) У класі навчаються 30 учнів, серед яких 13 хлопчиків та 17 дівчаток. Скільки способами можна сформувати команду з 7 учнів цього класу, якщо до неї повинна входити хоча б одна дівчинка?

Кількість всіх можливих команд по 7 осіб із класу дорівнює \(C_(30)^7\). Кількість команд у яких лише хлопчики - \ (C_ (13) ^ 7 \). Отже, кількість команд, у яких є хоча б одна дівчинка, дорівнює $$C_(30)^7 - C_(13)^7 =\frac(30{7!\cdot 23!} - \frac{13!}{7!\cdot 6!}=2~035~800-1~716=2~034~084.$$Ответ: 2 034 084. !} ◄

Поєднання з повтореннями

Крім звичайних поєднаньрозглядають поєднання з повтореннями .

Нехай у безлічі є n об'єктів. Виберемо з них m штук, діючи за таким принципом. Візьмемо будь-який, але не будемо його встановлювати в якийсь ряд, а просто запишемо, сам об'єкт після цього повернемо до інших. Потім знову з усіх n об'єктів виберемо один (у тому числі, можливо, і той, який було взято та записано раніше), запишемо його назву і знову повернемо об'єкт назад. І так далі, поки не отримаємо m назв.

Принципова відмінність від розміщень із повтореннями у тому, що у разі елементи списку не нумеруються. Наприклад, список "A, С, A, В"та список "А, А, В, С"вважаються однаковими.

Поєднання з повтореннями позначаються \(\overline(C)_n^m\) і обчислюються за формулою $$\overline(C)_n^m=P_(m,~n-1)=\frac((m+n-1 ){m!\cdot (n-1)!}.$$И ещё один способ записи той же формулы:$$\overline{C}_n^m=C_{m+n-1}^m=\frac{(m+n-1)!}{m!\cdot (n-1)!}.$$Заметим, что подобно размещениям с повторениями, допустим случай, когда !} m > n , тобто вибраних об'єктів більше, ніж їх є. Дійсно, кожен об'єкт після "використання" повертається назад і може бути використаний знову і знову.

Наприклад, з'ясуємо скільки можна купити 7 тістечок у кондитерському відділі, якщо у продажу 4 їх сорти?

Природно вважати, що кількість тістечок кожного виду не менше 7, і за бажання можна купити тільки тістечка одного з них. Так як порядок в якому кладуть куплені тістечка в коробку не важливий, маємо справу з поєднаннями з повтореннями. Так як потрібно вибрати 7 тістечок з 4 його видів, то кількість способів, що шукається, дорівнює:$$\overline(C)_4^7=\frac((7+4-1){7!\cdot (4-1)!}=\frac{10!}{7!\cdot 3!}=\frac{8\cdot 9\cdot 10}{1\cdot 2\cdot 3}=120.$$!}

Відповідь: 120. ◄

Біном Ньютона та біноміальні коефіцієнти

Рівність$$(x+a)^n=C_n^0x^na^0+C_n^1x^(n-1)a^1+...+C_n^mx^(n-m)a^m+...+ C_n^nx^0a^n$$називають біномом Ньютона або формулою Ньютона . Права частинарівності називається біноміальним розкладанням у суму а коефіцієнти \(C_n^0,~C_n^1,~...~,~C_n^n\) — біноміальними коефіцієнтами .

Властивості біномних коефіцієнтів:

\(~~~~~~~~1.~~C_n^0=C_n^n=1\\ ~~~~~~~~2.~~C_n^m=C_n^(n-m)\\ ~~ ~~~~~~3.~~C_n^m=C_(n-1)^(m-1)+C_(n-1)^(m)\\ ~~~~~~~~4.~ ~C_n^0+C_n^1+C_n^2+~...~+C_n^n=2^n\\ ~~~~~~~~5.~~C_n^0+C_n^2+C_n^ 4+~... =C_n^1+C_n^3+C_n^5+~...=2^(n-1)\\ ~~~~~~~~6.~~C_n^n+C_ (n+1)^n+C_(n+2)^n+~...~+C_(n+m-1)^n=C_(n+m)^(n+1)\\ \)

Властивості біномного розкладання:

1. Число всіх членів розкладання на одиницю більше за показник ступеня бінома,

тобто одно n+ 1 .

2. Сума показників ступенів x і a кожного члена розкладання дорівнює показнику ступеня бінома,

тобто (n - m) + m = n .

3. Загальний член розкладання (позначається T n+1 ) має вигляд$$T_(n+1)=C_n^m x^(n-m)a^m,~~~~m=0,~1,~2,~...~,~n.$$

Трикутник Паскаля

Усі можливі значення біномних коефіцієнтів (числа поєднань) для кожного показника ступеня бінома n можна записати у вигляді нескінченної трикутної таблиці. Така таблиця називається трикутником Паскаля:

					\(C_0^0\)
				\(C_1^0\)		\(C_1^1\)
			\(C_2^0\)		\(C_2^1\)		\(C_2^2\)
		\(C_3^0\)		\(C_3^1\)		\(C_3^2\)		\(C_3^3\)
	\(C_4^0\)		\(C_4^1\)		\(C_4^2\)		\(C_4^3\)		\(C_4^4\)
\(C_5^0\)		\(C_5^1\)		\(C_5^2\)		\(C_5^3\)		\(C_5^4\)		\(C_5^5\)
	. . .				. . .				. . .

У цьому трикутнику крайні числа у кожному рядку дорівнюють 1. Дійсно, \(C_n^0=C_n^n=1\). А кожне не крайнє число дорівнює сумі двох чисел попереднього рядка, що стоять над ним: \(C_n^m=C_(n-1)^(m-1)+C_(n-1)^(m)\).

Таким чином, цей трикутник пропонує ще один (рекурентний) спосіб обчислення чисел \(C_n^m\):

n = 0									1
n = 1								1		1
n = 2							1		2		1
n = 3						1		3		3		1
n = 4					1		4		6		4		1
n = 5				1		5		10		10		5		1
n = 6			1		6		15		20		15		6		1
n = 7		1		7		21		35		35		21		7		1
n = 8	1		8		28		56		70		56		28		8		1
...				...				...		...				...

Підрахуємо в MS EXCEL кількість перестановок із n елементів. За допомогою формул виведемо на лист усі варіанти перестановок ( англійський перекладтерміна: permutation).

Перестановкою множини з n елементів називається розташування елементів у певному порядку.

Елементами множини можуть бути числа, літери та взагалі будь-які об'єкти. Головне, щоб ці елементи були різними. Т.к. будь-якому об'єкту можна зіставити число, то для перестановок зазвичай використовують кінцеве безліч цілих чисел, наприклад, (1; 2; 3; 4; 5). Хоча безліч із літер також можна часто зустріти в літературі. Наприклад, всі різні Перестановки множини з трьох елементів (a, b, c) – це abc, acb, bac, bca, cab, cba.

Число Перестановок елементів n дорівнює n! (Факториал).

Для обчислення факторіалу в MS EXCEL є функція =ФАКТР() , англійський варіант FACT(). Відомо, що число перестановок зростає дуже швидко зі зростанням n: для n=7 число перестановок дорівнює 5040. Заради справедливості, слід зазначити, що найчастіше самі варіанти перестановок шукати не потрібно, головне – визначити їх кількість.

Примітка:Перестановки вважатимуться окремим випадком розміщень при n=k (див. статтю ). Тому для обчислення кількості перестановок можна використовувати функцію ПЕРЕСТ() . Для n=7 число перестановок обчислюється за такою формулою =ПЕРЕСТ(7;7)

Примітка: Про Перестановки з повтореннями (з поверненням елементів назад до множини, з якої вони беруться, після вибірки кожного елемента) можна прочитати у статті .

У прикладному файлі створена універсальна формула для виведення всіх Перестановок для заданого n. Наприклад, для n=3.

Завдання

6 машин різнихмарок беруть участь у гонках на виживання: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo. Визначити кількість можливих варіантів розподілу місць між усіма учасниками.

Нам потрібно визначити кількість перестановок 6 машин на 6 місцях. Тобто. n=6. Виявляється, таких перестановок 720: =ПЕРЕСТ(6;6) чи 6! =ФАКТР(6)

Скористайтеся прикладним файлом , щоб знайти всі варіанти перестановок.

Довільним чином порівняємо маркам машин числові значення та зробимо скорочення назв марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Ввівши в осередку В 5 значення 6, визначимо всі варіанти розміщення машин на зайнятих ними в гонці місцях.

Примітка: Про Розміщення можна прочитати у статті , а про Поєднання у статті .

Перебір усіх можливих перестановок може бути потрібним для вирішення різних завдань (див. статтю і ).

Інверсії перестановок

Для кожної перестановки a 1, a 2, a 3,..., a n з nцілих чисел 1, 2, 3, ..., n, інверсією називається пара ( a i, a j) якщо для i< j выполняется a i > a j. Число інверсією в перестановці показує, наскільки перестановка є "несортованою" за зростанням.

Наприклад, кількість інверсій у перестановці 1, 2, 3, 4 дорівнює 0 (перестановка з 4-х цілих чисел відсортована за зростанням від 1 до 4), а кількість інверсій у перестановці 4, 3, 1, 2 дорівнює 5, т.к .:

• перший елемент (i=1) дорівнює 4 і він більший 3-хчисел (з j=2, 3, 4), що розташовані правіше (4>3, 4>1, 4>2), тобто. ми маємо 3 інверсії;
• другий елемент (i=2) дорівнює 3 і він більший 2-хчисел (з j=3, 4), розташовані правіше (3>1, 3>2), тобто. ми маємо ще 2 інверсії;
• так третій елемент (i=3) дорівнює 1 і він менший від числа з j=4, яке розташоване правіше (1<2), то эта пара не является инверсией. Т.е. у перестановки 4, 3, 1, 2 число инверсий равно 3+2+0=5.

У прикладному файлі для кожної Перестановки підраховується кількість інверсій.