Хамгийн бага квадратын арга нь зарчим дээр суурилдаг. Асуудлыг шийдвэрлэх хамгийн бага квадратын арга
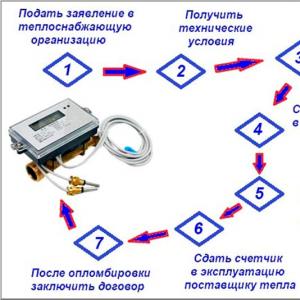
Хамгийн бага квадрат арга ( MNK, OLS, энгийн хамгийн бага квадратууд) - түүвэр өгөгдлөөс регрессийн загваруудын үл мэдэгдэх параметрүүдийг тооцоолох регрессийн шинжилгээний үндсэн аргуудын нэг. Энэ арга нь регрессийн үлдэгдэл квадратуудын нийлбэрийг багасгахад суурилдаг.
Шийдэл нь үл мэдэгдэх хувьсагчийн зарим функцын квадратуудын нийлбэрийг багасгах тодорхой шалгуураас бүрдсэн эсвэл хангасан тохиолдолд хамгийн бага квадратын аргыг өөрөө аль ч талбарт асуудлыг шийдвэрлэх арга гэж нэрлэж болно гэдгийг тэмдэглэх нь зүйтэй. Тиймээс хамгийн бага квадратын аргыг мөн ойролцоо дүрслэлд ашиглаж болно (ойролцоогоор) өгөгдсөн функцТоо нь эдгээр хэмжигдэхүүний тооноос давсан тэгшитгэл эсвэл хязгаарлалтыг хангасан хэмжигдэхүүний багцыг олох үед бусад (илүү энгийн) функцууд.
MNC-ийн мөн чанар
(тайлбарласан) хувьсагчийн хоорондох магадлалын (регрессийн) хамаарлын зарим (параметр) загварыг үзье. yболон олон хүчин зүйл (тайлбарлах хувьсагч) x
Үл мэдэгдэх загварын параметрийн вектор хаана байна
- Санамсаргүй загварын алдаа.Мөн заасан хувьсагчдын утгын түүврийн ажиглалтыг оруулаарай. Ажиглалтын дугаар () байг. Дараа нь --р ажиглалт дахь хувьсагчдын утгууд байна. Дараа нь b параметрийн өгөгдсөн утгуудын хувьд тайлбарласан y хувьсагчийн онолын (загвар) утгыг тооцоолох боломжтой.
Үлдэгдэлийн утга нь параметрийн утгаас хамаарна b.
LSM-ийн мөн чанар (энгийн, сонгодог) нь үлдэгдэл квадратуудын нийлбэр (eng. Квадратуудын үлдэгдэл нийлбэр) хамгийн бага байх болно:
AT ерөнхий тохиолдолэнэ асуудлыг шийдэж болно тоон аргуудоновчлол (багасгах). Энэ тохиолдолд нэг нь ярьдаг шугаман бус хамгийн бага квадратууд(NLS эсвэл NLLS - Англи. Шугаман бус хамгийн бага квадратууд). Ихэнх тохиолдолд аналитик шийдлийг олж авч болно. Багасгах асуудлыг шийдэхийн тулд үл мэдэгдэх b параметрүүдтэй харьцуулан ялгах, деривативуудыг тэгтэй тэнцүүлэх, үүссэн тэгшитгэлийн системийг шийдвэрлэх замаар функцийн суурин цэгүүдийг олох шаардлагатай.
Загварын санамсаргүй алдаа нь хэвийн тархалттай, ижил хэлбэлзэлтэй, өөр хоорондоо хамааралгүй бол хамгийн бага квадратын параметрийн тооцоолол нь хамгийн их магадлалтай аргын (MLM) тооцоололтой ижил байна.
Шугаман загварын хувьд LSM
Болъё регрессийн хамааралшугаман байна:
Болъё y- тайлбарласан хувьсагчийн ажиглалтын баганын вектор ба - хүчин зүйлийн ажиглалтын матриц (матрицын мөр - энэ ажиглалтын хүчин зүйлийн утгын векторууд, баганаар - утгын вектор энэ хүчин зүйлбүх ажиглалтанд). Шугаман загварын матриц дүрслэл нь дараах хэлбэртэй байна.
Дараа нь тайлбарласан хувьсагчийн үнэлгээний вектор ба регрессийн үлдэгдэл вектор нь тэнцүү байх болно.
үүний дагуу регрессийн үлдэгдлийн квадратуудын нийлбэр тэнцүү байна
Энэ функцийг параметрийн векторын хувьд ялгаж, деривативуудыг тэгтэй тэнцүүлэх замаар бид тэгшитгэлийн системийг (матриц хэлбэрээр) олж авна.
.Энэ тэгшитгэлийн системийн шийдэл нь өгдөг ерөнхий томъёоШугаман загварын OLS тооцоолол:
Аналитик зорилгоор энэ томъёоны сүүлчийн дүрслэл нь ашигтай болж хувирав. Хэрэв регрессийн загварт өгөгдөл төвтэй, тэгвэл энэ дүрслэлд эхний матриц нь хүчин зүйлсийн түүврийн ковариацын матрицын утгатай, хоёр дахь нь хамааралтай хувьсагчтай хүчин зүйлсийн ковариацын вектор юм. Хэрэв, үүнээс гадна, өгөгдөл нь мөн хэвийн болгосон SKO-д (энэ нь эцсийн эцэст стандартчилагдсан), тэгвэл эхний матриц нь хүчин зүйлийн түүвэр корреляцийн матриц, хоёр дахь вектор нь векторуудын утгыг агуулна. дээжийн хамааралхамааралтай хувьсагчтай хүчин зүйлүүд.
Загваруудын LLS тооцооны чухал шинж чанар тогтмолтой- баригдсан регрессийн шугам нь түүврийн өгөгдлийн хүндийн төвөөр дамждаг, өөрөөр хэлбэл тэгш байдал хангагдсан болно.
Ялангуяа онцгой тохиолдолд, цорын ганц регрессор тогтмол байх үед бид нэг параметрийн OLS үнэлгээ (тогтмол өөрөө) тайлбарлаж буй хувьсагчийн дундаж утгатай тэнцүү болохыг олж мэднэ. Энэ нь түүний арифметик дундаж юм сайн шинж чанаруудих тооны хуулиас энэ нь мөн хамгийн бага квадратын тооцоо юм - энэ нь түүнээс хазайсан квадратын хамгийн бага нийлбэрийн шалгуурыг хангадаг.
Жишээ нь: энгийн (хосоор) регресс
Уурын өрөөний хувьд шугаман регрессТооцооллын томъёог хялбаршуулсан (та матриц алгебргүйгээр хийж болно):
OLS тооцооны шинж чанарууд
Юуны өмнө бид шугаман загваруудын хувьд хамгийн бага квадратын тооцоолсон гэдгийг анхаарна уу шугаман тооцоолол, дээрх томъёоноос дараах байдлаар. Шударга бус хамгийн бага квадратын тооцоологчдын хувьд энэ нь зайлшгүй бөгөөд хангалттай юм зайлшгүй нөхцөлрегрессийн шинжилгээ: хүчин зүйлээс хамаарч санамсаргүй алдааны математик хүлээлт тэгтэй тэнцүү байх ёстой. Энэ нөхцөл, ялангуяа, хэрэв сэтгэл хангалуун байна
- хүлээгдэж буй үнэ цэнэсанамсаргүй алдаа нь тэг, ба
- хүчин зүйлс ба санамсаргүй алдаа нь бие даасан санамсаргүй хэмжигдэхүүн юм.
Хоёрдахь нөхцөл - экзоген хүчин зүйлийн нөхцөл нь суурь юм. Хэрэв энэ үл хөдлөх хөрөнгө хангагдаагүй бол бараг бүх тооцоо нь туйлын хангалтгүй байх болно гэж бид таамаглаж болно: тэдгээр нь бүр тогтвортой биш байх болно (өөрөөр хэлбэл маш их хэмжээний өгөгдөл ч гэсэн энэ тохиолдолд чанарын тооцоо хийх боломжийг олгодоггүй). Сонгодог тохиолдолд санамсаргүй алдаанаас ялгаатай нь хүчин зүйлийн детерминизмын талаар илүү хүчтэй таамаглал дэвшүүлсэн бөгөөд энэ нь автоматаар экзоген нөхцөл хангагдсан гэсэн үг юм. Ерөнхий тохиолдолд тооцооллыг тууштай байлгахын тулд түүврийн хэмжээ хязгааргүй хүртэл нэмэгдэж, матрицыг зарим нэг бус матрицад ойртуулахын хамт экзогенийн нөхцлийг биелүүлэхэд хангалттай.
Тохиромжтой, шударга байдлаас гадна (ердийн) хамгийн бага квадратуудын тооцоо нь үр дүнтэй байхын тулд (шугаман шударга бус үнэлгээний ангилалд хамгийн сайн нь) дараахь зүйлийг хийх шаардлагатай. нэмэлт шинж чанаруудсанамсаргүй алдаа:
Эдгээр таамаглалыг санамсаргүй алдааны векторын ковариацын матрицад зориулж томъёолж болно
Эдгээр нөхцлийг хангасан шугаман загварыг гэнэ сонгодог. Сонгодог шугаман регрессийн OLS тооцоолол нь бүх шугаман шударга бус тооцооллын ангилалд хамааралгүй, тууштай, хамгийн үр дүнтэй тооцоолол юм (Англи хэл дээрх товчлолыг заримдаа ашигладаг. цэнхэр (Шилдэг шугаман үндэслэлгүй тооцоологч) хамгийн сайн шугаман бус үнэлгээ; дотоодын уран зохиолд Гаусс-Марковын теоремыг илүү олон удаа иш татдаг). Үзүүлэхэд хялбар тул коэффициентийн тооцооллын векторын ковариацын матриц нь дараахтай тэнцүү байна.
Ерөнхийжүүлсэн хамгийн бага квадратууд
Хамгийн бага квадратын арга нь өргөн хүрээний ерөнхий ойлголт өгөх боломжийг олгодог. Үлдэгдэлийн квадратуудын нийлбэрийг багасгахын оронд үлдэгдэл векторын эерэг тодорхой квадрат хэлбэрийг багасгаж болно, энд зарим тэгш хэмтэй эерэг тодорхой жинтэй матриц байна. Жингийн матриц нь таних матрицтай пропорциональ байх үед энгийн хамгийн бага квадратууд нь энэ аргын онцгой тохиолдол юм. Тэгш хэмтэй матрицуудын (эсвэл операторуудын) онолоос мэдэгдэж байгаачлан ийм матрицуудын задрал байдаг. Тиймээс, заасан функцийг дараах байдлаар илэрхийлж болно, өөрөөр хэлбэл энэ функцийг зарим хувиргасан "үлдэгдэл" -ийн квадратуудын нийлбэрээр илэрхийлж болно. Тиймээс бид хамгийн бага квадратын аргуудын ангиллыг ялгаж салгаж болно - LS арга (Бага квадратууд).
Ерөнхий шугаман регрессийн загварын хувьд (санамсаргүй алдааны ковариацын матрицад хязгаарлалт тавьдаггүй) хамгийн үр дүнтэй (шугаман бус үнэлгээний ангилалд) гэж нэрлэгддэг тооцоолол байдаг нь (Айткенийн теорем) батлагдсан. ерөнхий OLS (OMNK, GLS - Ерөнхий жижиг квадратууд)- Санамсаргүй алдааны урвуу ковариацын матрицтай тэнцүү жинтэй матрицтай LS-арга: .
Шугаман загварын параметрүүдийн GLS-үнэлгээний томъёо нь хэлбэртэй байгааг харуулж болно
Эдгээр тооцооллын ковариацын матриц нь тэнцүү байх болно
Үнэн хэрэгтээ OLS-ийн мөн чанар нь анхны өгөгдлийн тодорхой (шугаман) хувиргалт (P) болон хувирсан өгөгдөлд ердийн хамгийн бага квадратуудыг ашиглахад оршдог. Энэхүү хувиргалтын зорилго нь хувиргасан өгөгдлийн хувьд санамсаргүй алдаа нь сонгодог таамаглалыг аль хэдийн хангасан байх явдал юм.
Жинлэсэн хамгийн бага квадратууд
Диагональ жингийн матриц (мөн санамсаргүй алдааны ковариацын матриц) тохиолдолд бид хамгийн бага жинтэй квадратууд гэж нэрлэгддэг (WLS - Weighted Least Squares). AT Энэ тохиолдолдзагварын үлдэгдлийн квадратуудын жигнэсэн нийлбэрийг багасгасан, өөрөөр хэлбэл, ажиглалт бүр энэ ажиглалтын санамсаргүй алдааны дисперстэй урвуу хамааралтай "жин"-ийг хүлээн авдаг: . Үнэн хэрэгтээ, өгөгдлийг ажиглалтыг жинлэх замаар (тооцоолсон хэмжээтэй пропорциональ хэмжээгээр хуваах) өөрчилдөг. стандарт хэлбэлзэлсанамсаргүй алдаа), харин жинлэсэн өгөгдөлд ердийн хамгийн бага квадратуудыг ашигладаг.
LSM-ийг практикт хэрэглэх зарим онцгой тохиолдлууд
Шугаман ойртолт
Тодорхой скаляр хэмжигдэхүүнийг тодорхой скаляр хэмжигдэхүүнээс хамаарлыг судалсны үр дүнд (Энэ нь жишээлбэл, хүчдэлийн гүйдлийн хүчнээс хамаарах хамаарал байж болно: , тогтмол утга хаана байна, дамжуулагчийн эсэргүүцэл). ), эдгээр хэмжигдэхүүнийг хэмжсэн бөгөөд үүний үр дүнд утгууд нь харгалзах утгыг олж авав. Хэмжилтийн өгөгдлийг хүснэгтэд тэмдэглэнэ.
Хүснэгт. Хэмжилтийн үр дүн.
| Хэмжилтийн дугаар | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Асуулт нь: коэффициентийн ямар утгыг сонгох боломжтой хамгийн зөв замдонтолтыг тайлбарлана уу? Хамгийн бага квадратуудын дагуу энэ утга нь утгуудын утгуудын квадрат хазайлтын нийлбэр байх ёстой.
хамгийн бага байсан
Квадрат хазайлтын нийлбэр нь нэг экстремумтай байдаг - хамгийн бага нь энэ томъёог ашиглах боломжийг бидэнд олгодог. Энэ томъёоноос коэффициентийн утгыг олъё. Үүнийг хийхийн тулд үүнийг өөрчилье зүүн талдараах байдлаар:
Сүүлийн томъёо нь асуудалд шаардлагатай байсан коэффициентийн утгыг олох боломжийг бидэнд олгодог.
Өгүүллэг
Өмнө нь XIX эхэн үе in. эрдэмтэд байгаагүй тодорхой дүрэмүл мэдэгдэх тоо нь тэгшитгэлийн тооноос бага байх тэгшитгэлийн системийг шийдвэрлэх; Тэр үеийг хүртэл тэгшитгэлийн төрөл, тооны машинуудын авъяас чадвараас хамааран тодорхой аргуудыг ашигладаг байсан тул ижил ажиглалтын өгөгдлөөс эхлэн өөр өөр тооны машинууд өөр өөр дүгнэлтэд хүрч байв. Гаусс (1795) аргын анхны хэрэглээ гэж тооцогддог бөгөөд Лежендре (1805) үүнийг бие даан олж, орчин үеийн нэрээр хэвлүүлсэн (fr. Арга зүй des moindres arres ). Лаплас энэ аргыг магадлалын онолтой холбосон бөгөөд Америкийн математикч Адрейн (1808) түүний магадлалын хэрэглээг авч үзсэн. Энэ арга нь Энке, Бессел, Хансен болон бусад хүмүүсийн цаашдын судалгаагаар өргөн тархсан бөгөөд сайжруулсан.
MNC-ийн альтернатив хэрэглээ
Хамгийн бага квадратын аргын санааг шууд хамааралгүй бусад тохиолдолд ашиглаж болно регрессийн шинжилгээ. Баримт нь квадратуудын нийлбэр нь векторуудын хамгийн түгээмэл ойрын хэмжүүрүүдийн нэг юм (хязгаарлагдмал хэмжээст орон зай дахь Евклидийн хэмжүүр).
Нэг хэрэглээ бол тэгшитгэлийн тоо нь хувьсагчийн тооноос их байх шугаман тэгшитгэлийн системийг "шийдвэрлэх" явдал юм.
матриц нь дөрвөлжин биш, харин тэгш өнцөгт хэлбэртэй байна.
Ийм тэгшитгэлийн систем нь ерөнхий тохиолдолд ямар ч шийдэлгүй (хэрэв зэрэглэл нь хувьсагчийн тооноос их байвал). Иймээс энэ системийг зөвхөн векторуудын хоорондох "зай"-ыг багасгахын тулд ийм векторыг сонгох утгаар л "шийдвэрлэх" боломжтой. Үүнийг хийхийн тулд та зүүн ба хоёрын квадрат ялгааны нийлбэрийг багасгах шалгуурыг ашиглаж болно. зөв хэсгүүдсистемийн тэгшитгэл, өөрөөр хэлбэл. Энэхүү багасгах бодлогын шийдэл нь дараах тэгшитгэлийн системийн шийдэлд хүргэдэг болохыг харуулахад хялбар байдаг
- заавар
Оршил
Би компьютерийн програмист мэргэжилтэй. Би ингэж хэлж сурснаар карьертаа хамгийн том үсрэлтийг хийсэн. "Би юу ч ойлгохгүй байна!"Одоо би шинжлэх ухааны гэгээнтэн надад лекц уншиж байна гэж хэлэхээс ичдэггүй, тэр гэгээнтэн надтай юу яриад байгааг ойлгохгүй байна. Бас их хэцүү. Тийм ээ, мэдэхгүй гэдгээ хүлээн зөвшөөрөх нь хэцүү бөгөөд ичмээр юм. Ямар нэгэн зүйлийн үндсийг мэдэхгүй гэдгээ хүлээн зөвшөөрөх дуртай хүн - тэнд. Мэргэжлээрээ би оролцох ёстой олон тоогоорилтгэл, лекц, би хүлээн зөвшөөрч байна, ихэнх тохиолдолд би юу ч ойлгохгүй байгаа тул унтахыг хүсдэг. Том асуудал учраас ойлгохгүй байна. Одоогийн нөхцөл байдалшинжлэх ухаанд математикт оршдог. Энэ нь бүх оюутнууд математикийн бүх салбарыг мэддэг (энэ нь утгагүй зүйл) гэж үздэг. Дериватив гэж юу болохыг мэдэхгүй гэдгээ хүлээн зөвшөөрөх нь (энэ нь арай хожуу юм) ичмээр юм.
Харин үржүүлэх гэж юу байдгийг мэдэхгүй гэж хэлж сурсан. Тийм ээ, би Лие алгебрийн дэд алгебр гэж юу болохыг мэдэхгүй. Тийм ээ, чамд яагаад амьдралд хэрэгтэй байгааг би мэдэхгүй квадрат тэгшитгэл. Дашрамд хэлэхэд, хэрэв та мэдэж байгаа гэдэгтээ итгэлтэй байвал бидэнд ярих зүйл байна! Математик бол хэд хэдэн заль мэх юм. Математикчид олон нийтийг төөрөгдүүлж, айлгах гэж оролддог; төөрөгдөл, нэр хүнд, эрх мэдэл байхгүй газар. Тийм ээ, аль болох хийсвэр хэлээр ярих нь нэр хүндтэй бөгөөд энэ нь өөрөө шал дэмий зүйл юм.
Дериватив гэж юу болохыг та мэдэх үү? Ялгаатай харьцааны хязгаарыг та надад хэлэх байх. Санкт-Петербургийн Улсын Их Сургуулийн математикийн нэгдүгээр курст Виктор Петрович Хавин намайг тодорхойлсонцэг дэх функцийн Тейлорын цувралын эхний гишүүний коэффициент гэж дериватив (энэ нь деривативгүйгээр Тейлорын цувралыг тодорхойлох тусдаа гимнастик байсан). Энэ тодорхойлолтыг би эцэст нь юу болохыг ойлгох хүртлээ удаан хугацаанд инээв. Дериватив гэдэг нь бидний ялгаж буй функц y=x, y=x^2, y=x^3 функцтэй хэр зэрэг төстэй болохыг харуулах хэмжүүрээс өөр зүйл биш юм.
Одоо би оюутнуудад лекц унших нэр хүндтэй болсон айдасматематик. Хэрэв та математикаас айдаг бол бид замдаа байна. Та зарим нэг текстийг унших гэж оролдоход энэ нь хэтэрхий төвөгтэй юм шиг санагдаж байвал үүнийг муу бичсэн гэдгийг мэдээрэй. Нарийвчлалыг алдалгүйгээр "хуруугаар" ярих боломжгүй математикийн нэг ч салбар байдаггүй гэж би баталж байна.
Ойрын ирээдүйн сорилт: Би сурагчдадаа шугаман-квадрат хянагч гэж юу болохыг ойлгохыг зааварласан. Бүү ичиж, амьдралынхаа гурван минутыг дэмий үрээрэй, холбоосыг дагана уу. Хэрэв та юу ч ойлгохгүй байвал бид явж байна. Би (мэргэжлийн математикч-програмист) бас юу ч ойлгосонгүй. Үүнийг "хуруугаар" шийдэж болно гэдгийг би танд баталж байна. Одоогоор энэ нь юу болохыг би мэдэхгүй, гэхдээ бид үүнийг олж мэдэх болно гэдгийг би танд баталж байна.
Тиймээс, шугаман квадрат хянагч бол таны амьдралд хэзээ ч эзэмшиж чадахгүй аймшигт алдаа юм гэсэн үгсээр айж гүйж ирсний дараа миний оюутнуудад хэлэх эхний лекц бол хамгийн бага квадратын аргууд. Та шийдэж чадах уу шугаман тэгшитгэл? Хэрэв та энэ текстийг уншиж байгаа бол уншихгүй байх магадлалтай.
Тиймээс (x0, y0), (x1, y1), жишээлбэл (1,1) ба (3,2) гэсэн хоёр цэгийг өгснөөр эдгээр хоёр цэгийг дайран өнгөрөх шулуун шугамын тэгшитгэлийг олох даалгавар байна.
дүрслэл
Энэ шулуун шугам нь дараахь тэгшитгэлтэй байх ёстой.
Энд альфа ба бета нь бидэнд мэдэгддэггүй, гэхдээ энэ шугамын хоёр цэг нь мэдэгдэж байна:
Та энэ тэгшитгэлийг матриц хэлбэрээр бичиж болно.
Энд та хийх ёстой уянгын хазайлт: матриц гэж юу вэ? Матриц нь хоёр хэмжээст массиваас өөр зүйл биш юм. Энэ бол өгөгдөл хадгалах арга бөгөөд түүнд илүү үнэ цэнэ өгөх ёсгүй. Тодорхой матрицыг яг яаж тайлбарлах нь биднээс шалтгаална. Би үүнийг үе үе шугаман зураглал, үе үе квадрат хэлбэр, заримдаа зүгээр л векторуудын багц гэж тайлбарлах болно. Энэ бүгдийг контекстийн хүрээнд тодруулах болно.
Тодорхой матрицуудыг тэдгээрийн бэлгэдлийн дүрслэлээр орлъё:
Дараа нь (альфа, бета) амархан олно:
Бидний өмнөх өгөгдлийн талаар илүү дэлгэрэнгүй:
Энэ нь (1,1) ба (3,2) цэгүүдийг дайран өнгөрөх шулуун шугамын тэгшитгэлд хүргэдэг:
За, энд бүх зүйл тодорхой байна. Тэгээд дайран өнгөрөх шулуун шугамын тэгшитгэлийг олъё гуравоноо: (x0,y0), (x1,y1) ба (x2,y2):
Өө-өө-өө, гэхдээ бидэнд хоёр үл мэдэгдэх гурван тэгшитгэл байна! Стандарт математикч ямар ч шийдэл байхгүй гэж хэлэх болно. Програмист юу гэж хэлэх вэ? Тэгээд тэр эхлээд өмнөх тэгшитгэлийн системийг дараах хэлбэрээр дахин бичих болно.
Манай тохиолдолд i,j,b векторуудЭдгээр нь гурван хэмжээст тул (ерөнхий тохиолдолд) энэ системийн шийдэл байхгүй. Аливаа вектор (alpha\*i + beta\*j) векторуудын (i, j) хүрээлэгдсэн хавтгайд оршдог. Хэрэв b нь энэ хавтгайд хамаарахгүй бол шийдэл байхгүй (тэгшитгэл дэх тэгш байдлыг хангах боломжгүй). Юу хийх вэ? Буултыг хайцгаая. -ээр тэмдэглэе e(альфа, бета)Бид яг яаж тэгш байдалд хүрч чадаагүй вэ?
Мөн бид энэ алдааг багасгахыг хичээх болно:
Яагаад дөрвөлжин гэж?
Бид нормын хамгийн бага хэмжээг биш, харин нормативын квадратын доод хэмжээг эрэлхийлж байна. Яагаад? Хамгийн бага цэг нь өөрөө давхцаж, квадрат нь гөлгөр функцийг өгдөг (аргументуудын квадрат функц (альфа, бета)), харин зөвхөн урт нь конус хэлбэрээр функцийг өгдөг бөгөөд хамгийн бага цэг дээр ялгагдахгүй. Брр. Талбай нь илүү тохиромжтой.
Мэдээжийн хэрэг, вектор үед алдаа багасдаг двекторуудаар тархсан хавтгайд ортогональ биболон j.
Дүрслэл
Өөрөөр хэлбэл, бид бүх цэгээс энэ шугам хүртэлх зайны квадрат уртын нийлбэр хамгийн бага байх шугамыг хайж байна.
ШИНЭЧЛЭЛ: Энд би түгжээтэй байна, шугам хүртэлх зайг босоо байдлаар хэмжих ёстой, зөв бичгийн проекц биш. Энэ сэтгэгдэл бичсэн хүн зөв.
Дүрслэл
Шал өөр үгээр (болгоомжтой, муу албан ёсны, гэхдээ энэ нь хуруун дээр тодорхой байх ёстой): бид бүх хос цэгүүдийн хоорондох бүх боломжит шугамыг авч, бүгдийн хоорондох дундаж шугамыг хайдаг.
Дүрслэл
Хуруун дээрх өөр нэг тайлбар: бид бүх өгөгдлийн цэгүүд (энд гурван байна) болон бидний хайж буй шугамын хооронд хавар хавсаргасан бөгөөд тэнцвэрийн төлөвийн шугам нь яг бидний хайж буй зүйл юм.
Квадрат хэлбэрийн хамгийн бага
Тиймээс векторыг өгсөн бматрицын багана-векторуудаар дамжсан хавтгай А(энэ тохиолдолд (x0,x1,x2) ба (1,1,1)) бид векторыг хайж байна. дхамгийн бага квадрат урттай. Мэдээжийн хэрэг, хамгийн багадаа зөвхөн векторын хувьд хүрэх боломжтой д, матрицын багана-векторуудаар дамжсан хавтгайд ортогональ А:Өөрөөр хэлбэл, бид x=(альфа, бета) векторыг хайж байна.
Энэ вектор x=(альфа, бета) хамгийн бага гэдгийг би танд сануулж байна квадрат функц||e(альфа, бета)||^2:
Энд матрицыг квадрат хэлбэрээс гадна тайлбарлаж болно гэдгийг санах нь зүйтэй, жишээлбэл, таних матриц((1,0),(0,1))-ийг x^2 + y^2 функц гэж тайлбарлаж болно:
квадрат хэлбэр
Энэ бүх гимнастикийг шугаман регресс гэж нэрлэдэг.
Дирихлегийн хилийн нөхцөлтэй Лапласын тэгшитгэл
Одоо хамгийн энгийн бодит асуудал: тодорхой гурвалжин гадаргуу байгаа тул үүнийг тэгшлэх шаардлагатай. Жишээлбэл, миний нүүрний загварыг ачаалъя:
Анхны амлалт бэлэн байна. Гадны хамаарлыг багасгахын тулд би Habré дээр байгаа программ хангамжийнхаа кодыг авсан. Шийдлийн хувьд шугаман системБи OpenNL ашигладаг, энэ нь маш сайн шийддэг, гэхдээ суулгахад үнэхээр хэцүү: та хоёр файлыг (.h+.c) төслийн хавтас руу хуулах хэрэгтэй. Бүх тэгшитгэх ажлыг дараах кодоор гүйцэтгэнэ.
For (int d=0; d<3; d++) {
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, verts.size());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<(int)verts.size(); i++) {
nlBegin(NL_ROW);
nlCoefficient(i, 1);
nlRightHandSide(verts[i][d]);
nlEnd(NL_ROW);
}
for (unsigned int i=0; i
X, Y, Z координатуудыг салгах боломжтой, би тэдгээрийг тусад нь тэгшитгэдэг. Өөрөөр хэлбэл, би загварынхаа оройн тоотой ижил тооны хувьсагчтай шугаман тэгшитгэлийн гурван системийг шийддэг. А матрицын эхний n мөрөнд нэг мөрөнд зөвхөн нэг 1, b векторын эхний n мөрөнд анхны загвар координатууд байна. Өөрөөр хэлбэл, би шинэ оройн байрлал болон хуучин оройн байрлалыг хооронд нь холбодог - шинэ нь хуучин цэгүүдээс хэт хол байх ёсгүй.
А матрицын дараачийн бүх мөрүүд (faces.size()*3 = сүлжээн дэх бүх гурвалжны ирмэгийн тоо) нь 1-ийн нэг тохиолдол, -1-ийн нэг илрэлтэй байхад b вектор нь эсрэг талын тэг бүрэлдэхүүнтэй байна. Энэ нь би гурвалжин торны ирмэг бүр дээр пүрш тавьсан гэсэн үг юм: бүх ирмэгүүд нь эхлэл ба төгсгөлийн цэгүүдтэй ижил оройг авахыг хичээдэг.
Дахин нэг удаа: бүх орой нь хувьсах хэмжигдэхүүн бөгөөд тэдгээр нь анхны байрлалаасаа хол хазайж чадахгүй, гэхдээ нэгэн зэрэг тэд бие биетэйгээ төстэй байхыг хичээдэг.
Үр дүн нь энд байна:
Бүх зүйл сайхан байх болно, загвар нь үнэхээр гөлгөр болсон, гэхдээ энэ нь анхны ирмэгээсээ холдсон. Кодоо бага зэрэг өөрчилье:
For (int i=0; i<(int)verts.size(); i++) { float scale = border[i] ? 1000: 1; nlBegin(NL_ROW); nlCoefficient(i, scale); nlRightHandSide(scale*verts[i][d]); nlEnd(NL_ROW); }
Манай А матрицад ирмэг дээр байгаа оройнуудын хувьд би v_i = verts[i][d] ангиллаас мөр биш, харин 1000*v_i = 1000*verts[i][d] нэмдэг. Энэ нь юу өөрчлөгддөг вэ? Энэ нь алдааны квадрат хэлбэрийг өөрчилдөг. Одоо ирмэг дээр дээрээс нэг хазайлт нь өмнөх шигээ нэг нэгж биш, харин 1000 * 1000 нэгж болно. Өөрөөр хэлбэл, бид туйлын орой дээр илүү хүчтэй булаг өлгөж, шийдэл нь бусдыг илүү хүчтэй сунгахыг илүүд үздэг. Үр дүн нь энд байна:
Оройнуудын хоорондох булгийн хүчийг хоёр дахин нэмэгдүүлье.
nlКоэффицент(нүүр[ j ], 2); nlКоэффицент(нүүр[(j+1)%3], -2);
Гадаргуу нь илүү гөлгөр болсон нь логик юм.
Одоо бүр зуу дахин хүчтэй:
Энэ юу вэ? Бид утсан цагиргийг савантай усанд дүрсэн гэж төсөөлөөд үз дээ. Үүний үр дүнд үүссэн савангийн хальс нь аль болох хамгийн бага муруйлттай байхыг хичээж, ижил хил дээр - бидний утсан цагирагт хүрнэ. Хил засаад дотор нь гөлгөр гадаргуутай болгооч гэж гуйсан нь яг ийм юм. Баяр хүргэе, бид дөнгөж сая Лапласын тэгшитгэлийг Дирихлегийн хилийн нөхцлөөр шийдлээ. Сайхан сонсогдож байна уу? Гэвч үнэн хэрэгтээ шугаман тэгшитгэлийн нэг л системийг шийдэх хэрэгтэй.
Пуассоны тэгшитгэл
Өөр нэг сайхан нэртэй болцгооё.Надад ийм зураг байна гэж бодъё:
Бүгд сайн, гэхдээ би сандалдаа дургүй.
Би зургийг хагас болгон хуваасан: 
Тэгээд би өөрийн гараар сандал сонгох болно: 
Дараа нь би маск дээрх цагаан өнгөтэй бүх зүйлийг зургийн зүүн тал руу чирж, бүхэл бүтэн зураг дээр хоёр хөрш пикселийн ялгаа нь хоёр хөршийн пикселийн зөрүүтэй тэнцүү байх ёстой гэж хэлэх болно. зөв зураг:
For (int i=0; i Үр дүн нь энд байна: Код болон зураг байгаа Би компьютерийн програмист мэргэжилтэй. Би ингэж хэлж сурснаар карьертаа хамгийн том үсрэлтийг хийсэн. "Би юу ч ойлгохгүй байна!"Одоо би шинжлэх ухааны гэгээнтэн надад лекц уншиж байна гэж хэлэхээс ичдэггүй, тэр гэгээнтэн надтай юу яриад байгааг ойлгохгүй байна. Бас их хэцүү. Тийм ээ, мэдэхгүй гэдгээ хүлээн зөвшөөрөх нь хэцүү бөгөөд ичмээр юм. Ямар нэгэн зүйлийн үндсийг мэдэхгүй гэдгээ хүлээн зөвшөөрөх дуртай хүн - тэнд. Мэргэжлийнхээ ачаар би олон тооны илтгэл, лекцэнд оролцох ёстой бөгөөд ихэнх тохиолдолд би юу ч ойлгодоггүй тул нойрмог байдаг. Шинжлэх ухааны өнөөгийн нөхцөл байдлын томоохон асуудал математикт оршдог тул би ойлгохгүй байна. Энэ нь бүх оюутнууд математикийн бүх салбарыг мэддэг (энэ нь утгагүй зүйл) гэж үздэг. Дериватив гэж юу болохыг мэдэхгүй гэдгээ хүлээн зөвшөөрөх нь (энэ нь арай хожуу юм) ичмээр юм. Харин үржүүлэх гэж юу байдгийг мэдэхгүй гэж хэлж сурсан. Тийм ээ, би Лие алгебрийн дэд алгебр гэж юу болохыг мэдэхгүй. Тийм ээ, яагаад квадрат тэгшитгэл амьдралд хэрэгтэйг мэдэхгүй байна. Дашрамд хэлэхэд, хэрэв та мэдэж байгаа гэдэгтээ итгэлтэй байвал бидэнд ярих зүйл байна! Математик бол хэд хэдэн заль мэх юм. Математикчид олон нийтийг төөрөгдүүлж, айлгах гэж оролддог; төөрөгдөл, нэр хүнд, эрх мэдэл байхгүй газар. Тийм ээ, аль болох хийсвэр хэлээр ярих нь нэр хүндтэй бөгөөд энэ нь өөрөө шал дэмий зүйл юм. Одоо би оюутнуудад лекц унших нэр хүндтэй болсон айдасматематик. Хэрэв та математикаас айдаг бол бид замдаа байна. Та зарим нэг текстийг унших гэж оролдоход энэ нь хэтэрхий төвөгтэй юм шиг санагдаж байвал үүнийг муу бичсэн гэдгийг мэдээрэй. Нарийвчлалыг алдалгүйгээр "хуруугаар" ярих боломжгүй математикийн нэг ч салбар байдаггүй гэж би баталж байна. Ойрын ирээдүйн сорилт: Би сурагчдадаа шугаман-квадрат хянагч гэж юу болохыг ойлгохыг зааварласан. Бүү ичиж, амьдралынхаа гурван минутыг дэмий үрээрэй, холбоосыг дагана уу. Хэрэв та юу ч ойлгохгүй байвал бид явж байна. Би (мэргэжлийн математикч-програмист) бас юу ч ойлгосонгүй. Үүнийг "хуруугаар" шийдэж болно гэдгийг би танд баталж байна. Одоогоор энэ нь юу болохыг би мэдэхгүй, гэхдээ бид үүнийг олж мэдэх болно гэдгийг би танд баталж байна. Тиймээс, шугаман квадрат хянагч бол таны амьдралд хэзээ ч эзэмшиж чадахгүй аймшигт алдаа юм гэсэн үгсээр айж гүйж ирсний дараа миний оюутнуудад хэлэх эхний лекц бол хамгийн бага квадратын аргууд. Та шугаман тэгшитгэлийг шийдэж чадах уу? Хэрэв та энэ текстийг уншиж байгаа бол уншихгүй байх магадлалтай. Тиймээс (x0, y0), (x1, y1), жишээлбэл (1,1) ба (3,2) гэсэн хоёр цэгийг өгснөөр эдгээр хоёр цэгийг дайран өнгөрөх шулуун шугамын тэгшитгэлийг олох даалгавар байна. дүрслэл Энэ шулуун шугам нь дараахь тэгшитгэлтэй байх ёстой. Энд альфа ба бета нь бидэнд мэдэгддэггүй, гэхдээ энэ шугамын хоёр цэг нь мэдэгдэж байна: Та энэ тэгшитгэлийг матриц хэлбэрээр бичиж болно. Энд бид уянгын ухралт хийх ёстой: матриц гэж юу вэ? Матриц нь хоёр хэмжээст массиваас өөр зүйл биш юм. Энэ бол өгөгдөл хадгалах арга бөгөөд түүнд илүү үнэ цэнэ өгөх ёсгүй. Тодорхой матрицыг яг яаж тайлбарлах нь биднээс шалтгаална. Би үүнийг үе үе шугаман зураглал, үе үе квадрат хэлбэр, заримдаа зүгээр л векторуудын багц гэж тайлбарлах болно. Энэ бүгдийг контекстийн хүрээнд тодруулах болно. Тодорхой матрицуудыг тэдгээрийн бэлгэдлийн дүрслэлээр орлъё: Дараа нь (альфа, бета) амархан олно: Бидний өмнөх өгөгдлийн талаар илүү дэлгэрэнгүй: Энэ нь (1,1) ба (3,2) цэгүүдийг дайран өнгөрөх шулуун шугамын тэгшитгэлд хүргэдэг: За, энд бүх зүйл тодорхой байна. Тэгээд дайран өнгөрөх шулуун шугамын тэгшитгэлийг олъё гуравоноо: (x0,y0), (x1,y1) ба (x2,y2): Өө-өө-өө, гэхдээ бидэнд хоёр үл мэдэгдэх гурван тэгшитгэл байна! Стандарт математикч ямар ч шийдэл байхгүй гэж хэлэх болно. Програмист юу гэж хэлэх вэ? Тэгээд тэр эхлээд өмнөх тэгшитгэлийн системийг дараах хэлбэрээр дахин бичих болно. Манай тохиолдолд i, j, b векторууд гурван хэмжээст тул (ерөнхий тохиолдолд) энэ системийн шийдэл байхгүй байна. Аливаа вектор (alpha\*i + beta\*j) векторуудын (i, j) хүрээлэгдсэн хавтгайд оршдог. Хэрэв b нь энэ хавтгайд хамаарахгүй бол шийдэл байхгүй (тэгшитгэл дэх тэгш байдлыг хангах боломжгүй). Юу хийх вэ? Буултыг хайцгаая. -ээр тэмдэглэе e(альфа, бета)Бид яг яаж тэгш байдалд хүрч чадаагүй вэ? Мөн бид энэ алдааг багасгахыг хичээх болно: Яагаад дөрвөлжин гэж? Бид нормын хамгийн бага хэмжээг биш, харин нормативын квадратын доод хэмжээг эрэлхийлж байна. Яагаад? Хамгийн бага цэг нь өөрөө давхцаж, квадрат нь гөлгөр функцийг өгдөг (аргументуудын квадрат функц (альфа, бета)), харин зөвхөн урт нь конус хэлбэрээр функцийг өгдөг бөгөөд хамгийн бага цэг дээр ялгагдахгүй. Брр. Талбай нь илүү тохиромжтой. Мэдээжийн хэрэг, вектор үед алдаа багасдаг двекторуудаар тархсан хавтгайд ортогональ биболон j. Дүрслэл Өөрөөр хэлбэл, бид бүх цэгээс энэ шугам хүртэлх зайны квадрат уртын нийлбэр хамгийн бага байх шугамыг хайж байна. ШИНЭЧЛЭЛ: Энд би түгжээтэй байна, шугам хүртэлх зайг босоо байдлаар хэмжих ёстой, зөв бичгийн проекц биш. сэтгэгдэл бичсэн хүний зөв. Дүрслэл Шал өөр үгээр (болгоомжтой, муу албан ёсны, гэхдээ энэ нь хуруун дээр тодорхой байх ёстой): бид бүх хос цэгүүдийн хоорондох бүх боломжит шугамыг авч, бүгдийн хоорондох дундаж шугамыг хайдаг. Дүрслэл Хуруун дээрх өөр нэг тайлбар: бид бүх өгөгдлийн цэгүүд (энд гурван байна) болон бидний хайж буй шугамын хооронд хавар хавсаргасан бөгөөд тэнцвэрийн төлөвийн шугам нь яг бидний хайж буй зүйл юм. Өөрөөр хэлбэл, бид x=(альфа, бета) векторыг хайж байна. Энэ вектор x=(альфа, бета) нь ||e(альфа, бета)||^2 квадрат функцын хамгийн бага хэмжээ гэдгийг би танд сануулж байна: Энд матрицыг квадрат хэлбэрээс гадна тайлбарлах боломжтой гэдгийг санах нь зүйтэй, жишээлбэл, таних матрицыг ((1,0),(0,1)) x^2 + y функц гэж тайлбарлаж болно. ^2: квадрат хэлбэр Энэ бүх гимнастикийг шугаман регресс гэж нэрлэдэг. Анхны амлалт бэлэн байна. Гадны хамаарлыг багасгахын тулд би Habré дээр байгаа программ хангамжийнхаа кодыг авсан. Шугаман системийг шийдэхийн тулд би OpenNL ашигладаг, энэ нь маш сайн шийдэгч боловч суулгахад маш хэцүү: та хоёр файлыг (.h + .c) төслийн хавтас руу хуулах хэрэгтэй. Бүх тэгшитгэх ажлыг дараах кодоор гүйцэтгэнэ. For (int d=0; d<3; d++) {
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, verts.size());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<(int)verts.size(); i++) {
nlBegin(NL_ROW);
nlCoefficient(i, 1);
nlRightHandSide(verts[i][d]);
nlEnd(NL_ROW);
}
for (unsigned int i=0; i X, Y, Z координатуудыг салгах боломжтой, би тэдгээрийг тусад нь тэгшитгэдэг. Өөрөөр хэлбэл, би загварынхаа оройн тоотой ижил тооны хувьсагчтай шугаман тэгшитгэлийн гурван системийг шийддэг. А матрицын эхний n мөрөнд нэг мөрөнд зөвхөн нэг 1, b векторын эхний n мөрөнд анхны загвар координатууд байна. Өөрөөр хэлбэл, би шинэ оройн байрлал болон хуучин оройн байрлалыг хооронд нь холбодог - шинэ нь хуучин цэгүүдээс хэт хол байх ёсгүй. А матрицын дараачийн бүх мөрүүд (faces.size()*3 = сүлжээн дэх бүх гурвалжны ирмэгийн тоо) нь 1-ийн нэг тохиолдол, -1-ийн нэг илрэлтэй байхад b вектор нь эсрэг талын тэг бүрэлдэхүүнтэй байна. Энэ нь би гурвалжин торны ирмэг бүр дээр пүрш тавьсан гэсэн үг юм: бүх ирмэгүүд нь эхлэл ба төгсгөлийн цэгүүдтэй ижил оройг авахыг хичээдэг. Дахин нэг удаа: бүх орой нь хувьсах хэмжигдэхүүн бөгөөд тэдгээр нь анхны байрлалаасаа хол хазайж чадахгүй, гэхдээ нэгэн зэрэг тэд бие биетэйгээ төстэй байхыг хичээдэг. Үр дүн нь энд байна: Бүх зүйл сайхан байх болно, загвар нь үнэхээр гөлгөр болсон, гэхдээ энэ нь анхны ирмэгээсээ холдсон. Кодоо бага зэрэг өөрчилье: For (int i=0; i<(int)verts.size(); i++) {
float scale = border[i] ? 1000: 1;
nlBegin(NL_ROW);
nlCoefficient(i, scale);
nlRightHandSide(scale*verts[i][d]);
nlEnd(NL_ROW);
}
Манай А матрицад ирмэг дээр байгаа оройнуудын хувьд би v_i = verts[i][d] ангиллаас мөр биш, харин 1000*v_i = 1000*verts[i][d] нэмдэг. Энэ нь юу өөрчлөгддөг вэ? Энэ нь алдааны квадрат хэлбэрийг өөрчилдөг. Одоо ирмэг дээр дээрээс нэг хазайлт нь өмнөх шигээ нэг нэгж биш, харин 1000 * 1000 нэгж болно. Өөрөөр хэлбэл, бид туйлын орой дээр илүү хүчтэй булаг өлгөж, шийдэл нь бусдыг илүү хүчтэй сунгахыг илүүд үздэг. Үр дүн нь энд байна: Оройнуудын хоорондох булгийн хүчийг хоёр дахин нэмэгдүүлье. Гадаргуу нь илүү гөлгөр болсон нь логик юм. Одоо бүр зуу дахин хүчтэй: Энэ юу вэ? Бид утсан цагиргийг савантай усанд дүрсэн гэж төсөөлөөд үз дээ. Үүний үр дүнд үүссэн савангийн хальс нь аль болох хамгийн бага муруйлттай байхыг хичээж, ижил хил дээр - бидний утсан цагирагт хүрнэ. Хил засаад дотор нь гөлгөр гадаргуутай болгооч гэж гуйсан нь яг ийм юм. Баяр хүргэе, бид дөнгөж сая Лапласын тэгшитгэлийг Дирихлегийн хилийн нөхцлөөр шийдлээ. Сайхан сонсогдож байна уу? Гэвч үнэн хэрэгтээ шугаман тэгшитгэлийн нэг л системийг шийдэх хэрэгтэй. Надад ийм зураг байна гэж бодъё: Бүгд сайн, гэхдээ би сандалдаа дургүй. Би зургийг хагас болгон хуваасан: Тэгээд би өөрийн гараар сандал сонгох болно: Дараа нь би маск дээрх цагаан өнгөтэй бүх зүйлийг зургийн зүүн тал руу чирж, бүхэл бүтэн зураг дээр хоёр хөрш пикселийн ялгаа нь хоёр хөршийн пикселийн зөрүүтэй тэнцүү байх ёстой гэж хэлэх болно. зөв зураг: For (int i=0; i Үр дүн нь энд байна: Код болон зураг байгаа Жишээ. Хувьсагчийн утгын туршилтын өгөгдөл Xболон цагтхүснэгтэд өгөгдсөн. Тэдний тохируулгын үр дүнд функц Ашиглаж байна хамгийн бага квадрат арга, эдгээр өгөгдлийг шугаман хамаарлаар ойролцоол y=ax+b(параметрүүдийг олох аболон б). Туршилтын өгөгдлүүдийг зэрэгцүүлж байгаа хоёр мөрийн аль нь илүү дээр болохыг олж мэд (хамгийн бага квадратын аргын утгаараа). Зураг зурах. Асуудал нь хоёр хувьсагчийн функцийг гүйцэтгэх шугаман хамаарлын коэффициентийг олох явдал юм аболон б
Ийнхүү жишээний шийдэл нь хоёр хувьсагчийн функцийн экстремумыг олох хүртэл буурдаг. Хоёр үл мэдэгдэх хоёр тэгшитгэлийн системийг эмхэтгэж, шийддэг. Функцийн хэсэгчилсэн деривативуудыг олох Бид үүссэн тэгшитгэлийн системийг ямар ч аргаар шийддэг (жишээлбэл орлуулах аргаэсвэл Крамерын арга) ба хамгийн бага квадратын аргыг (LSM) ашиглан коэффициентийг олох томъёог олж авна. Өгөгдлийн хамт аболон бфункц Энэ бол хамгийн бага квадратуудын бүх арга юм. Параметрийг олох томъёо анийлбэр,,, параметрийг агуулна n- туршилтын өгөгдлийн хэмжээ. Эдгээр дүнгийн утгыг тусад нь тооцоолохыг зөвлөж байна. Коэффицент бтооцооны дараа олдсон а. Анхны жишээг санах цаг болжээ. Шийдэл. Бидний жишээнд n=5. Шаардлагатай коэффициентүүдийн томъёонд орсон дүнг тооцоолоход хялбар болгох үүднээс бид хүснэгтийг бөглөнө. Хүснэгтийн дөрөв дэх эгнээний утгыг тоо бүрийн 2-р эгнээний утгыг 3-р эгнээний утгуудаар үржүүлэх замаар олж авна. би. Хүснэгтийн тав дахь эгнээний утгыг тоо тус бүрийн 2-р эгнээний утгыг квадрат болгох замаар олж авна. би. Хүснэгтийн сүүлчийн баганын утгууд нь мөр хоорондын утгуудын нийлбэр юм. Коэффициентийг олохын тулд бид хамгийн бага квадратын аргын томъёог ашигладаг аболон б. Бид тэдгээрт хүснэгтийн сүүлчийн баганаас харгалзах утгуудыг орлуулна. Үүний үр дүнд, у=0,165х+2,184нь хүссэн ойролцоох шулуун шугам юм. Энэ мөрүүдийн аль нь болохыг олж мэдэх л үлдлээ у=0,165х+2,184эсвэл Үүнийг хийхийн тулд та эдгээр мөрүүдээс анхны өгөгдлийн квадрат хазайлтын нийлбэрийг тооцоолох хэрэгтэй оноос хойш, дараа нь шугам у=0,165х+2,184анхны өгөгдлийг илүү сайн ойртуулдаг. График дээр бүх зүйл сайхан харагдаж байна. Улаан шугам нь олсон шугам юм у=0,165х+2,184, цэнхэр шугам нь Практикт янз бүрийн үйл явцыг загварчлахдаа, тухайлбал эдийн засаг, физик, техникийн, нийгмийн - зарим тогтмол цэгүүдэд мэдэгдэж буй утгуудаас функцүүдийн ойролцоо утгыг тооцоолох эдгээр эсвэл бусад аргыг өргөн ашигладаг. Энэ төрлийн функцийг ойртуулах асуудал ихэвчлэн гарч ирдэг. туршилтын үр дүнд олж авсан хүснэгтийн өгөгдлийн дагуу судалж буй үйл явцын шинж чанарын утгыг тооцоолох ойролцоо томъёог бүтээхдээ; тоон интеграл, дифференциал, дифференциал тэгшитгэлийг шийдвэрлэх гэх мэт; хэрэв авч үзсэн интервалын завсрын цэгүүдэд функцүүдийн утгыг тооцоолох шаардлагатай бол; авч үзэж буй интервалаас гадуурх үйл явцын шинж чанарын утгыг тодорхойлох, ялангуяа урьдчилан таамаглах үед. Хүснэгтээр тодорхойлсон тодорхой процессыг загварчлахын тулд хамгийн бага квадратын аргад тулгуурлан энэ процессыг ойролцоогоор тодорхойлсон функцийг байгуулвал түүнийг ойролцоолох функц (регресс) гэж нэрлэх ба ойролцоох функцийг бүтээх ажил өөрөө болно. ойролцоолох асуудал байх. Энэхүү нийтлэлд ийм асуудлыг шийдвэрлэх MS Excel багцын боломжуудын талаар авч үзэх бөгөөд үүнээс гадна хүснэгтээр өгөгдсөн функцүүдийн регрессийг бий болгох (бүтээх) арга, арга техникийг (энэ нь регрессийн шинжилгээний үндэс болсон) өгсөн болно. Excel дээр регресс үүсгэх хоёр сонголт байдаг. Сонгосон регрессийг (тренд шугам) судалж буй үйл явцын шинж чанарын өгөгдлийн хүснэгтэд үндэслэн бүтээсэн диаграмд нэмэх (зөвхөн диаграммыг барьсан тохиолдолд л боломжтой); Excel-ийн ажлын хуудасны суурилагдсан статистик функцийг ашиглах нь эх өгөгдлийн хүснэгтээс шууд регресс (трэнд шугам) авах боломжийг олгодог. Диаграммд чиг хандлагын шугам нэмэх Тодорхой үйл явцыг дүрсэлсэн, диаграмаар дүрсэлсэн өгөгдлийн хүснэгтийн хувьд Excel нь регрессийн шинжилгээний үр дүнтэй хэрэгсэлтэй бөгөөд танд дараахь зүйлийг хийх боломжийг олгодог. хамгийн бага квадратын аргын үндсэн дээр барьж, диаграммд судалж буй процессыг янз бүрийн нарийвчлалтайгаар загварчлах таван төрлийн регрессийг нэмэх; Диаграммд баригдсан регрессийн тэгшитгэлийг нэмэх; сонгосон регрессийн диаграммд үзүүлсэн өгөгдөлтэй нийцэж байгаа зэргийг тодорхойлох. Графикийн өгөгдөл дээр үндэслэн Excel нь тэгшитгэлээр өгөгдсөн шугаман, олон гишүүнт, логарифм, хүч, экспоненциал регрессийн төрлийг авах боломжийг олгодог. у = у(х) Энд x нь бие даасан хувьсагч бөгөөд энэ нь ихэвчлэн натурал тоонуудын дарааллын утгыг (1; 2; 3; ...) авч, жишээлбэл, судалж буй процессын цагийг тоолох (шинж чанар) үүсгэдэг. . 1
. Шугаман регресс нь тогтмол хурдаар нэмэгдэж, буурах шинж чанарыг загварчлахад сайн байдаг. Энэ бол судалж буй үйл явцын хамгийн энгийн загвар юм. Энэ нь тэгшитгэлийн дагуу бүтээгдсэн: y=mx+b Энд m нь шугаман регрессийн налуугийн шүргэгч х тэнхлэг; b - шугаман регрессийн y тэнхлэгтэй огтлолцох цэгийн координат. 2
. Олон гишүүнт чиг хандлагын шугам нь хэд хэдэн эрс тэс (өндөр ба доод) шинж чанаруудыг тодорхойлоход хэрэгтэй. Олон гишүүнтийн зэргийг сонгох нь судалж буй шинж чанарын экстремумуудын тоогоор тодорхойлогддог. Тиймээс хоёр дахь зэрэглэлийн олон гишүүнт нь зөвхөн нэг хамгийн их эсвэл хамгийн багатай процессыг сайн тодорхойлж чадна; гуравдугаар зэргийн олон гишүүнт - хоёр экстремумаас илүүгүй; дөрөвдүгээр зэргийн олон гишүүнт - гурваас илүүгүй экстремум гэх мэт. Энэ тохиолдолд чиг хандлагын шугамыг тэгшитгэлийн дагуу байгуулна. y = c0 + c1x + c2x2 + c3x3 + c4x4 + c5x5 + c6x6 Энд c0, c1, c2,... c6 коэффициентүүд нь барилгын ажлын явцад тодорхойлогддог тогтмолууд юм. 3
. Логарифмын чиг хандлагын шугамыг загварчлалд амжилттай ашигладаг бөгөөд тэдгээрийн утгууд нь эхлээд хурдан өөрчлөгдөж, дараа нь аажмаар тогтворждог. y = c ln(x) + b 4
. Хэрэв судлагдсан хамаарлын утгууд нь өсөлтийн хурдны тогтмол өөрчлөлтөөр тодорхойлогддог бол эрчим хүчний чиг хандлагын шугам нь сайн үр дүнг өгдөг. Ийм хамаарлын жишээ нь машины жигд хурдассан хөдөлгөөний график болж болно. Хэрэв өгөгдөлд тэг эсвэл сөрөг утга байгаа бол та эрчим хүчний чиг хандлагын шугамыг ашиглах боломжгүй. Энэ нь тэгшитгэлийн дагуу баригдсан: y = cxb b, c коэффициентүүд нь тогтмол байна. 5
. Өгөгдлийн өөрчлөлтийн хурд тасралтгүй нэмэгдэж байвал экспоненциал чиг хандлагын шугамыг ашиглах хэрэгтэй. Тэг эсвэл сөрөг утгатай өгөгдлийн хувьд энэ төрлийн ойролцооллыг мөн ашиглах боломжгүй. Энэ нь тэгшитгэлийн дагуу баригдсан: y=cebx b, c коэффициентүүд нь тогтмол байна. Трендийн шугамыг сонгохдоо Excel нь R2-ийн утгыг автоматаар тооцдог бөгөөд энэ нь ойролцоогоор тооцооллын нарийвчлалыг тодорхойлдог: R2 утга нь нэгд ойртох тусам чиг хандлагын шугам нь судалж буй процессыг илүү найдвартай ойртуулдаг. Шаардлагатай бол R2-ийн утгыг диаграм дээр үргэлж харуулж болно. Томъёогоор тодорхойлно: Өгөгдлийн цувралд чиг хандлагын шугам нэмэхийн тулд: өгөгдлийн цувралын үндсэн дээр бүтээгдсэн диаграмыг идэвхжүүлэх, өөрөөр хэлбэл диаграмын талбар дотор товш. Үндсэн цэсэнд Chart зүйл гарч ирнэ; Энэ зүйл дээр товшсоны дараа дэлгэцэн дээр цэс гарч ирэх бөгөөд үүнд та Trend мөр нэмэх командыг сонгох хэрэгтэй. Хэрэв та өгөгдлийн цувралын аль нэгэнд тохирох график дээр хулганы баруун товчийг дарвал ижил үйлдлүүдийг хялбархан гүйцэтгэх болно; гарч ирэх контекст цэснээс Add Trend line командыг сонгоно. Тренд шугамын харилцах цонх нь Type tab-ыг нээсэн үед дэлгэцэн дээр гарч ирнэ (Зураг 1). Үүний дараа танд хэрэгтэй: Төрөл таб дээрээс шаардлагатай чиг хандлагын шугамын төрлийг сонгоно уу (Анхдагчаар шугаманыг сонгосон). Олон гишүүнт төрлийн хувьд Degree талбарт сонгосон олон гишүүнтийн зэргийг зааж өгнө. 1
. Built on Series талбар нь тухайн диаграм дахь бүх өгөгдлийн цувралуудыг жагсаадаг. Тодорхой өгөгдлийн цувралд чиг хандлагын шугам нэмэхийн тулд Built on series талбараас нэрийг нь сонгоно уу. Шаардлагатай бол "Параметр" таб (Зураг 2) руу орж, чиг хандлагын шугамын хувьд дараах параметрүүдийг тохируулж болно. Ойролцоо (гөлгөр) муруй талбарын нэр дэх трендийн шугамын нэрийг өөрчлөх. Урьдчилан таамаглах талбарт урьдчилан таамаглах хугацааны тоог (урагш эсвэл урагш) тохируулах; диаграмын талбарт чиг хандлагын шугамын тэгшитгэлийг харуулах ба үүний тулд диаграм дээрх тэгшитгэлийг харуулах хайрцгийг идэвхжүүлэх хэрэгтэй; диаграмын талбарт R2 ойртсон найдвартай байдлын утгыг харуулах ба үүний тулд та диаграмм дээр ойртсон найдвартай байдлын утгыг (R^2) тэмдэглэгээг идэвхжүүлэх хэрэгтэй; чиг хандлагын шугамын Y тэнхлэгтэй огтлолцох цэгийг тохируулах ба үүний тулд та муруйг Y тэнхлэгтэй цэг дээр огтлолцох нүдийг идэвхжүүлэх хэрэгтэй; OK товчийг дарж харилцах цонхыг хаа. Аль хэдийн бий болсон тренд шугамыг засварлаж эхлэх гурван арга бий: чиг хандлагын шугамыг сонгосны дараа Формат цэсний Сонгосон чиг хандлагын шугам командыг ашиглана; чиг хандлагын шугам дээр хулганы баруун товчийг дарж дуудагдах контекст цэснээс Format Trendline командыг сонгоно уу; чиг хандлагын шугам дээр давхар товших замаар. Тренд шугамыг форматлах харилцах цонх дэлгэцэн дээр гарч ирнэ (Зураг 3), Харах, Төрөл, Параметр гэсэн гурван табыг агуулсан бөгөөд сүүлийн хоёрын агуулга нь Trendline харилцах цонхны ижил төстэй табуудтай бүрэн давхцаж байна (Зураг 1-2). ). Харах таб дээр та шугамын төрөл, түүний өнгө, зузааныг тохируулж болно. Аль хэдийн бий болсон трендийн шугамыг устгахын тулд устгах трендийн шугамыг сонгоод Delete товчийг дарна уу. Регрессийн шинжилгээний хэрэгслийн давуу талууд нь: Трендийн шугамыг график дээр өгөгдлийн хүснэгт үүсгэхгүйгээр зурах харьцангуй хялбар байдал; санал болгож буй чиг хандлагын шугамын төрлүүдийн нэлээд өргөн жагсаалт бөгөөд энэ жагсаалтад хамгийн түгээмэл хэрэглэгддэг регрессийн төрлүүд багтсан болно; судалж буй үйл явцын зан үйлийг дур зоргоороо (ерөнхий ойлголтоор) урагшлах, түүнчлэн ухрах алхмуудыг урьдчилан таамаглах боломж; чиг хандлагын шугамын тэгшитгэлийг аналитик хэлбэрээр авах боломж; шаардлагатай бол ойролцоогоор тооцооллын найдвартай байдлын үнэлгээг авах боломж. Сул талууд нь дараахь зүйлийг агуулна. чиг хандлагын шугамыг барих нь зөвхөн цуврал өгөгдөл дээр суурилсан диаграм байгаа тохиолдолд л хийгддэг; Тренд шугамын тэгшитгэл дээр үндэслэн судалж буй шинж чанарын өгөгдлийн цуваа үүсгэх үйл явц нь бага зэрэг эмх замбараагүй байдаг: шаардлагатай регрессийн тэгшитгэлүүд нь анхны өгөгдлийн цувралын утгын өөрчлөлт бүрээр шинэчлэгддэг, гэхдээ зөвхөн диаграмын хүрээнд. , хуучин шугамын тэгшитгэлийн чиг хандлагын үндсэн дээр үүссэн өгөгдлийн цуваа өөрчлөгдөөгүй хэвээр байна; Пивот диаграмын тайланд диаграмын харагдац эсвэл холбогдох Пивот хүснэгтийн тайланг өөрчлөх үед одоо байгаа чиг хандлагын шугамууд хадгалагдахгүй тул та чиг хандлагын шугам зурах эсвэл Пивот диаграмын тайланг өөр хэлбэрээр форматлахаас өмнө тайлангийн бүтэц таны шаардлагад нийцэж байгаа эсэхийг шалгах хэрэгтэй. График, гистограмм, хавтгай нормчлогдоогүй талбайн диаграм, бар, тараалт, хөөс, хувьцааны график зэрэг диаграммд үзүүлсэн өгөгдлийн цувралд чиг хандлагын шугамыг нэмж болно. Та 3-D, Стандарт, Радар, Pie, Donut диаграм дээрх өгөгдлийн цувралд чиг хандлагын шугам нэмэх боломжгүй. Суурилуулсан Excel функцуудыг ашиглах Excel нь диаграмын талбайн гадна чиг хандлагын шугамыг зурах регрессийн шинжилгээний хэрэгслээр хангадаг. Энэ зорилгоор статистикийн ажлын хуудасны хэд хэдэн функцийг ашиглаж болох боловч тэдгээр нь бүгд зөвхөн шугаман эсвэл экспоненциал регрессийг бүтээх боломжийг олгодог. Excel нь шугаман регрессийг бий болгох хэд хэдэн функцтэй, тухайлбал: TREND; SLOPE болон CUT. Экспоненциал чиг хандлагын шугамыг бий болгох хэд хэдэн функц, тухайлбал: LGRFPойролцоо. TREND болон ӨСӨЛТ функцийг ашиглан регрессийг бий болгох арга техник нь бараг ижил гэдгийг тэмдэглэх нь зүйтэй. LINEST болон LGRFPRIBL хос функцүүдийн талаар мөн адил зүйлийг хэлж болно. Эдгээр дөрвөн функцийн хувьд утгын хүснэгт үүсгэхдээ массивын томьёо гэх мэт Excel функцуудыг ашигладаг бөгөөд энэ нь регрессийг бий болгох үйл явцыг тодорхой хэмжээгээр саатуулдаг. Шугаман регрессийн бүтээн байгуулалт нь бидний бодлоор SLOPE ба INTERCEPT функцуудыг ашиглан хэрэгжүүлэхэд хамгийн хялбар гэдгийг бид тэмдэглэж, тэдгээрийн эхнийх нь шугаман регрессийн налууг, хоёр дахь нь регрессээр таслагдсан сегментийг тодорхойлдог. y тэнхлэг дээр. Регрессийн шинжилгээнд зориулсан суулгасан функцийн хэрэгслийн давуу талууд нь: чиг хандлагын шугамыг тогтоодог бүх суурилагдсан статистик функцүүдийн судалж буй шинж чанарын өгөгдлийн цуваа үүсгэх ижил төрлийн нэлээд энгийн процесс; үүсгэсэн өгөгдлийн цуврал дээр үндэслэн чиг хандлагын шугамыг бий болгох стандарт техник; шаардлагатай тооны урагш эсвэл ухрах алхмуудын хувьд судалж буй үйл явцын зан төлөвийг урьдчилан таамаглах чадвар. Сул тал нь Excel-д бусад (шугаман ба экспоненциал) төрлийн чиг хандлагын шугамыг бий болгох суурилуулсан функцүүд байдаггүй. Энэ нөхцөл байдал нь ихэвчлэн судалж буй үйл явцын хангалттай үнэн зөв загварыг сонгох, бодит байдалд ойртсон урьдчилсан мэдээг олж авах боломжийг олгодоггүй. Түүнчлэн, TREND болон GROW функцийг ашиглах үед чиг хандлагын шугамын тэгшитгэлүүд тодорхойгүй байдаг. Зохиогчид өгүүллийн зорилгоо регрессийн шинжилгээний явцыг янз бүрийн бүрэн дүүрэн байдлаар танилцуулах зорилго тавиагүй гэдгийг тэмдэглэх нь зүйтэй. Үүний гол зорилго нь тодорхой жишээнүүдийг ашиглан ойролцоолсон асуудлыг шийдвэрлэхэд Excel багцын чадварыг харуулах явдал юм; регресс болон таамаглалыг бий болгоход Excel-д ямар үр дүнтэй хэрэгсэл байгааг харуулах; Регрессийн шинжилгээний талаар гүнзгий мэдлэггүй хэрэглэгч ч гэсэн ийм асуудлыг харьцангуй амархан шийдэж болохыг харуулах. Тодорхой асуудлыг шийдвэрлэх жишээ Excel багцын жагсаасан хэрэгслүүдийг ашиглан тодорхой асуудлуудын шийдлийг авч үзье. Даалгавар 1 Автотээврийн аж ахуйн нэгжийн 1995-2002 оны ашгийн талаархи мэдээллийн хүснэгттэй. та дараах зүйлийг хийх хэрэгтэй. График бүтээх. Диаграммд шугаман болон олон гишүүнт (квадрат ба куб) чиг хандлагын шугамыг нэмнэ үү. Тренд шугамын тэгшитгэлийг ашиглан 1995-2004 оны чиг хандлагын шугам тус бүрээр аж ахуйн нэгжийн ашгийн талаарх хүснэгтэн мэдээллийг олж авна. Аж ахуйн нэгжийн 2003, 2004 оны ашгийн таамаглалыг гаргах. Асуудлын шийдэл Excel-ийн ажлын хуудасны A4: C11 нүднүүдийн хүрээнд бид Зураг дээр үзүүлсэн ажлын хуудсыг оруулна. дөрөв. B4:C11 нүднүүдийн мужийг сонгосны дараа бид диаграммыг байгуулна. Бид бүтээгдсэн диаграмыг идэвхжүүлж, дээр дурдсан аргын дагуу Trend Line харилцах цонхноос чиг хандлагын шугамын төрлийг сонгосны дараа (1-р зургийг үз) графикт шугаман, квадрат, куб трендийн шугамуудыг ээлжлэн нэмнэ. Ижил харилцах цонхонд Параметр табыг нээнэ үү (Зураг 2-ыг үз), ойролцоох (тэгшгэсэн) муруй талбарт нэмсэн трендийн нэрийг оруулаад, Forecast forward for: periods талбарт утгыг тохируулна уу. 2, ойрын хоёр жилийн ашгийн таамаглал гаргахаар төлөвлөж байгаа тул. Диаграммын талбарт регрессийн тэгшитгэл болон ойролцоолсон найдвартай байдлын утгыг R2 харуулахын тулд дэлгэцэн дээрх тэгшитгэлийг харуулах хайрцгийг идэвхжүүлж, диаграмм дээр ойртсон найдвартай байдлын утгыг (R^2) байрлуулна. Илүү сайн харагдахын тулд бид бий болгосон чиг хандлагын шугамын төрөл, өнгө, зузааныг өөрчилдөг бөгөөд үүний тулд Trend Line Format харилцах цонхны Харах табыг ашигладаг (3-р зургийг үз). Нэмэлт чиг хандлагын шугам бүхий үр дүнгийн графикийг Зураг дээр үзүүлэв. 5. 1995-2004 оны чиг хандлагын шугам тус бүрээр аж ахуйн нэгжийн ашгийн талаархи хүснэгтэн мэдээллийг авах. Зураг дээр үзүүлсэн чиг хандлагын шугамын тэгшитгэлийг ашиглацгаая. 5. Үүнийг хийхийн тулд D3:F3 мужын нүднүүдэд сонгосон трендийн шугамын төрлийн тухай текстэн мэдээллийг оруулна: Шугаман тренд, Квадрат тренд, Куб тренд. Дараа нь D4 нүдэнд шугаман регрессийн томъёог оруулаад дүүргэх тэмдэглэгээг ашиглан энэ томьёог D5:D13 нүднүүдийн мужид харьцангуй лавлагаатайгаар хуулна. D4:D13 нүдний мужаас шугаман регрессийн томьёотой нүд бүр аргумент болгон A4:A13 мужаас харгалзах нүдтэй байгааг тэмдэглэх нь зүйтэй. Үүний нэгэн адил квадрат регрессийн хувьд E4:E13 нүдний мужийг, куб регрессийн хувьд F4:F13 нүдний мужийг дүүргэнэ. Ийнхүү аж ахуйн нэгжийн 2003, 2004 оны ашгийн урьдчилсан тооцоо гарсан. гурван чиг хандлагатай. Үр дүнгийн утгын хүснэгтийг Зураг дээр үзүүлэв. 6. Даалгавар 2 График бүтээх. Диаграммд логарифм, экспоненциал, экспоненциал чиг хандлагын шугамыг нэмнэ үү. Хүлээн авсан чиг хандлагын шугамын тэгшитгэл, түүнчлэн R2 найдвартай байдлын утгыг тус бүрээр нь гарга. Тренд шугамын тэгшитгэлийг ашиглан 1995-2002 оны чиг хандлагын шугам тус бүрийн аж ахуйн нэгжийн ашгийн талаарх хүснэгтэн мэдээллийг олж авна. Эдгээр чиг хандлагын шугамыг ашиглан 2003, 2004 оны бизнесийн ашгийн таамаглалыг гарга. Асуудлын шийдэл 1-р асуудлыг шийдвэрлэхэд өгөгдсөн аргачлалын дагуу бид логарифм, экспоненциал болон экспоненциал чиг хандлагын шугамыг нэмсэн диаграммыг олж авна (Зураг 7). Цаашилбал, олж авсан чиг хандлагын шугамын тэгшитгэлийг ашиглан бид 2003, 2004 оны таамагласан утгыг багтаасан аж ахуйн нэгжийн ашгийн утгын хүснэгтийг бөглөнө. (Зураг 8). Зураг дээр. 5 ба зураг. логарифмын хандлагатай загвар нь ойролцоогоор найдвартай байдлын хамгийн бага утгатай тохирч байгааг харж болно. R2 = 0.8659 R2-ийн хамгийн өндөр утга нь олон гишүүнт хандлагатай загваруудад тохирч байна: квадрат (R2 = 0.9263) ба куб (R2 = 0.933). Даалгавар 3 1-р даалгаварт өгөгдсөн 1995-2002 оны автотээврийн аж ахуйн нэгжийн ашгийн талаархи мэдээллийн хүснэгтийн дагуу та дараах алхмуудыг хийх ёстой. TREND болон GROW функцийг ашиглан шугаман болон экспоненциал чиг хандлагын шугамын өгөгдлийн цувралыг аваарай. TREND болон ӨСӨЛТ функцийг ашиглан аж ахуйн нэгжийн 2003, 2004 оны ашгийн таамаглалыг гарга. Эхний өгөгдөл болон хүлээн авсан өгөгдлийн цувралын хувьд диаграммыг байгуул. Асуудлын шийдэл 1-р даалгаврын ажлын хуудсыг ашиглацгаая (4-р зургийг үз). TREND функцээс эхэлье: D4: D11 нүднүүдийн мужийг сонгох бөгөөд энэ нь аж ахуйн нэгжийн ашгийн талаарх мэдэгдэж буй өгөгдөлд харгалзах TREND функцийн утгуудаар дүүргэгдсэн байх ёстой; Insert цэснээс Function командыг дуудна. Гарч ирэх функцийн шидтэн харилцах цонхноос Статистик ангилалаас TREND функцийг сонгоод OK товчийг дарна уу. Үүнтэй ижил үйлдлийг стандарт хэрэгслийн самбарын товчлуур (Insert функц) дарж хийж болно. Гарч буй "Функцийн аргументууд" харилцах цонхны "Мэдэгдэж буй_утга" талбарт C4:C11 нүдний мужийг оруулна; Мэдэгдэж буй_утга_х талбарт - B4:B11 нүдний муж; Оруулсан томъёог массив томьёо болгохын тулд + + товчлуурын хослолыг ашиглана. Томъёоны мөрөнд бидний оруулсан томьёо дараах байдалтай харагдана: =(TREND(C4:C11;B4:B11)). Үүний үр дүнд D4: D11 нүднүүдийн хүрээ нь TREND функцийн харгалзах утгуудаар дүүрсэн байна (Зураг 9). Компанийн 2003, 2004 оны ашгийн таамаглалыг гаргах. шаардлагатай: TREND функцээр урьдчилан таамагласан утгуудыг оруулах D12:D13 нүднүүдийн мужийг сонгоно уу. TREND функцийг дуудаж, гарч ирэх "Функцийн аргументууд" харилцах цонхонд "Мэдэгдэж буй_утга_у" талбарт C4:C11 нүдний мужийг оруулна уу; Мэдэгдэж буй_утга_х талбарт - B4:B11 нүдний муж; болон Шинэ_утга_x талбарт - B12:B13 нүдний муж. Ctrl + Shift + Enter товчлууруудыг ашиглан энэ томьёог массив томьёо болгон хувиргана уу. Оруулсан томьёо нь дараах байдлаар харагдах болно: =(TREND(C4:C11;B4:B11;B12:B13)), D12:D13 нүднүүдийн муж нь TREND функцийн урьдчилан таамагласан утгуудаар дүүрнэ (Зураг 1-ийг үз). 9). Үүний нэгэн адил өгөгдлийн цувралыг GROWTH функцийг ашиглан дүүргэдэг бөгөөд энэ нь шугаман бус хамаарлыг шинжлэхэд ашигладаг бөгөөд шугаман TREND-тэй яг адилхан ажилладаг. Зураг 10-д хүснэгтийг томъёоны дэлгэцийн горимд харуулав. Эхний өгөгдөл болон олж авсан өгөгдлийн цувралын хувьд диаграммыг Зураг дээр үзүүлэв. арван нэгэн. Даалгавар 4 Автотээврийн аж ахуйн нэгжийн диспетчерийн үйлчилгээ үзүүлэх хүсэлтийг тухайн сарын 1-ээс 11-ний өдрийг хүртэлх хугацаанд хүлээн авсан мэдээллийн хүснэгтийн дагуу дараахь үйлдлүүдийг хийх ёстой. Шугаман регрессийн өгөгдлийн цуваа авах: SLOPE болон INTERCEPT функцийг ашиглан; LINEST функцийг ашиглан. LYFFPRIB функцийг ашиглан экспоненциал регрессийн өгөгдлийн цувралыг татаж авна уу. Дээрх функцуудыг ашиглан тухайн сарын 12-оос 14-ний өдрийг хүртэлх хугацаанд диспетчерийн үйлчилгээнд өргөдөл хүлээн авах урьдчилсан мэдээг гарга. Анхны болон хүлээн авсан өгөгдлийн цувралын хувьд диаграммыг байгуул. Асуудлын шийдэл TREND болон GROW функцүүдээс ялгаатай нь дээр дурдсан функцүүдийн аль нь ч (SLOPE, INTERCEPTION, LINEST, LGRFPRIB) регресс биш гэдгийг анхаарна уу. Эдгээр функцууд нь зөвхөн туслах үүрэг гүйцэтгэдэг бөгөөд шаардлагатай регрессийн параметрүүдийг тодорхойлдог. SLOPE, INTERCEPT, LINEST, LGRFINB функцуудыг ашиглан бүтээгдсэн шугаман болон экспоненциал регрессийн хувьд тэдгээрийн тэгшитгэлийн харагдах байдал нь TREND ба ӨСӨЛТ функцэд харгалзах шугаман болон экспоненциал регрессээс ялгаатай нь үргэлж мэдэгддэг. 1
. Дараах тэгшитгэлтэй шугаман регрессийг байгуулъя. y=mx+b SLOPE болон INTERCEPT функцийг ашиглан регрессийн налууг m-ийг SLOPE функцээр, b тогтмол гишүүнийг INTERCEPT функцээр тодорхойлно. Үүнийг хийхийн тулд бид дараах үйлдлүүдийг гүйцэтгэдэг. A4:B14 нүдний мужид эх хүснэгтийг оруулна уу; m параметрийн утгыг C19 нүдэнд тодорхойлно. Статистикийн ангилалаас Slope функцийг сонгоно уу; мэдэгдэж байгаа_утга_y талбарт B4:B14 нүдний мужийг, мэдэгдэж буй_утга_х талбарт A4:A14 нүдний мужийг оруулна. Томьёог C19 нүдэнд оруулна: =SLOPE(B4:B14;A4:A14); ижил төстэй аргыг ашиглан D19 нүдний b параметрийн утгыг тодорхойлно. Үүний агуулга нь иймэрхүү харагдах болно: = INTERCEPT(B4:B14;A4:A14). Тиймээс шугаман регрессийг бий болгоход шаардлагатай m ба b параметрийн утгыг C19, D19 нүднүүдэд тус тус хадгална; Дараа нь бид шугаман регрессийн томъёог C4 нүдэнд: = $ C * A4 + $ D хэлбэрээр оруулна. Энэ томъёонд C19 ба D19 нүднүүд үнэмлэхүй лавлагаатай бичигдсэн байдаг (хуулбарлах замаар нүдний хаяг өөрчлөгдөх ёсгүй). Үнэмлэхүй лавлагааны тэмдгийг $ гараас эсвэл курсорыг нүдний хаяг дээр байрлуулсны дараа F4 товчлуурыг ашиглан бичиж болно. Бөглөх бариулыг ашиглан энэ томьёог C4:C17 нүдний мужид хуулна. Бид хүссэн өгөгдлийн цувралыг авдаг (Зураг 12). Хүсэлтийн тоо нь бүхэл тоо тул та Cell Format цонхны Number табын аравтын бутархайн тоог 0 болгож тооны форматыг тохируулах хэрэгтэй. 2
. Одоо тэгшитгэлээр өгөгдсөн шугаман регрессийг байгуулъя. y=mx+b LINEST функцийг ашиглан. Үүний тулд: C20:D20: =(LINEST(B4:B14;A4:A14)) нүднүүдийн мужид LINEST функцийг массивын томьёо болгон оруулна. Үүний үр дүнд бид C20 нүдэнд m параметрийн утгыг, D20 нүдэнд b параметрийн утгыг авна; D4 нүдэнд томьёог оруулна: =$C*A4+$D; дүүргэх тэмдэглэгээг ашиглан энэ томьёог D4:D17 нүднүүдийн мужид хуулж, хүссэн өгөгдлийн цувралыг аваарай. 3
. Бид дараах тэгшитгэлтэй экспоненциал регрессийг байгуулна. LGRFPRIBL функцийн тусламжтайгаар үүнийг дараах байдлаар гүйцэтгэдэг. C21:D21 нүдний мужид LGRFPRIBL функцийг массив томьёо болгон оруулна уу: =( LGRFPRIBL (B4:B14;A4:A14)). Энэ тохиолдолд m параметрийн утгыг C21 нүдэнд, b параметрийн утгыг D21 нүдэнд тодорхойлно; томъёог E4 нүдэнд оруулна: =$D*$C^A4; дүүргэх тэмдэглэгээг ашиглан энэ томьёог экспоненциал регрессийн өгөгдлийн цуваа байрлах E4:E17 нүднүүдийн мужид хуулна (12-р зургийг үз). Зураг дээр. 13-т шаардлагатай нүдний мужууд болон томъёогоор бидний ашигладаг функцуудыг харах боломжтой хүснэгтийг харуулав. Үнэ цэнэ Р
2
дуудсан тодорхойлох коэффициент. Регрессийн хамаарлыг бий болгох даалгавар нь R коэффициент хамгийн их утгыг авах загварын (1) m коэффициентүүдийн векторыг олох явдал юм. R-ийн ач холбогдлыг үнэлэхийн тулд томъёогоор тооцоолсон Фишерийн F тестийг ашигладаг хаана n- дээжийн хэмжээ (туршилтын тоо); k нь загварын коэффициентүүдийн тоо юм. Хэрэв F нь өгөгдлийн зарим чухал утгыг давсан бол nболон кболон хүлээн зөвшөөрөгдсөн итгэлийн түвшин, дараа нь R утгыг чухал ач холбогдолтой гэж үзнэ. F-ийн чухал утгуудын хүснэгтийг математик статистикийн лавлах номонд өгсөн болно. Тиймээс R-ийн ач холбогдлыг зөвхөн үнэ цэнээр нь биш, мөн туршилтын тоо болон загварын коэффициентүүдийн (параметрүүдийн) тоо хоорондын харьцаагаар тодорхойлдог. Үнэн хэрэгтээ энгийн шугаман загварын хувьд n=2 корреляцийн харьцаа 1 байна (хавтгай дээрх 2 цэгээр дамжуулан та үргэлж нэг шулуун шугам зурж болно). Гэсэн хэдий ч туршилтын өгөгдөл нь санамсаргүй хэмжигдэхүүн бол R-ийн ийм утгыг маш болгоомжтой итгэх хэрэгтэй. Ихэвчлэн мэдэгдэхүйц R ба найдвартай регрессийг олж авахын тулд туршилтын тоо нь загварын коэффициентүүдийн тооноос (n>k) ихээхэн давсан эсэхийг баталгаажуулахад чиглэгддэг. Шугаман регрессийн загварыг бий болгохын тулд та дараахь зүйлийг хийх ёстой. 1) туршилтын өгөгдлийг агуулсан n мөр, m баганын жагсаалтыг бэлтгэх (гаралтын утгыг агуулсан багана) Южагсаалтын эхний эсвэл сүүлчийнх байх ёстой); жишээлбэл, өмнөх даалгаврын өгөгдлийг авч, "үеийн дугаар" нэртэй баганыг нэмж, 1-ээс 12 хүртэлх үеийн тоог дугаарлана. (эдгээр нь утгууд байх болно) X) 2) Data/Data Analysis/Regression цэс рүү орно Хэрэв "Хэрэгслүүд" цэсний "Өгөгдлийн шинжилгээ" зүйл байхгүй бол та ижил цэсний "Нэмэлтүүд" хэсэгт очиж "Шинжилгээний багц" нүдийг шалгана уу. 3) "Регресс" харилцах цонхонд: оролтын интервал Y; оролтын интервал X; гаралтын интервал - тооцооллын үр дүнг байрлуулах интервалын зүүн дээд нүд (шинэ ажлын хуудсан дээр байрлуулахыг зөвлөж байна); 4) "Ok" дээр дарж үр дүнд дүн шинжилгээ хийнэ. Бид функцийг 2-р зэргийн олон гишүүнтээр ойртуулна. Үүнийг хийхийн тулд бид ердийн тэгшитгэлийн системийн коэффициентийг тооцоолно. , Хамгийн бага квадратуудын ердийн системийг зохиоё, энэ нь дараах хэлбэртэй байна. Системийн шийдлийг олоход хялбар:, , . Ийнхүү 2-р зэргийн олон гишүүнт олдлоо: . Онолын суурь Хуудас руу буцах<Введение в вычислительную математику. Примеры> Жишээ 2. Олон гишүүнтийн оновчтой зэрэглэлийг олох. Хуудас руу буцах<Введение в вычислительную математику. Примеры> Жишээ 3. Эмпирик хамаарлын параметрүүдийг олохын тулд хэвийн тэгшитгэлийн системийг гарган авах. Коэффициент ба функцийг тодорхойлох тэгшитгэлийн системийг гаргаж авцгаая Дараа нь ердийн систем дараах хэлбэрийг авна. Бид үл мэдэгдэх параметрүүдийн шугаман тэгшитгэлийн системийг олж авсан бөгөөд үүнийг амархан шийддэг. Онолын суурь Хуудас руу буцах<Введение в вычислительную математику. Примеры> Жишээ. Хувьсагчийн утгын туршилтын өгөгдөл Xболон цагтхүснэгтэд өгөгдсөн. Тэдний тохируулгын үр дүнд функц Ашиглаж байна хамгийн бага квадрат арга, эдгээр өгөгдлийг шугаман хамаарлаар ойролцоол y=ax+b(параметрүүдийг олох аболон б). Туршилтын өгөгдлүүдийг зэрэгцүүлж байгаа хоёр мөрийн аль нь илүү дээр болохыг олж мэд (хамгийн бага квадратын аргын утгаараа). Зураг зурах. Асуудал нь хоёр хувьсагчийн функцийг гүйцэтгэх шугаман хамаарлын коэффициентийг олох явдал юм аболон б Ийнхүү жишээний шийдэл нь хоёр хувьсагчийн функцийн экстремумыг олох хүртэл буурдаг. Хоёр үл мэдэгдэх хоёр тэгшитгэлийн системийг эмхэтгэж, шийддэг. Функцийн хэсэгчилсэн деривативуудыг олох Бид үүссэн тэгшитгэлийн системийг ямар ч аргаар шийддэг (жишээлбэл орлуулах аргаэсвэл Крамерын арга) ба хамгийн бага квадратын арга (LSM) ашиглан коэффициентийг олох томъёог олж авна. Өгөгдлийн хамт аболон бфункц Энэ бол хамгийн бага квадратуудын бүх арга юм. Параметрийг олох томъёо анийлбэр, , , параметрийг агуулна nтуршилтын өгөгдлийн хэмжээ юм. Эдгээр дүнгийн утгыг тусад нь тооцоолохыг зөвлөж байна. Коэффицент бтооцооны дараа олдсон а. Анхны жишээг санах цаг болжээ. Шийдэл. Бидний жишээнд n=5. Шаардлагатай коэффициентүүдийн томъёонд орсон дүнг тооцоолоход хялбар болгох үүднээс бид хүснэгтийг бөглөнө. Хүснэгтийн дөрөв дэх эгнээний утгыг тоо бүрийн 2-р эгнээний утгыг 3-р эгнээний утгуудаар үржүүлэх замаар олж авна. би. Хүснэгтийн тав дахь эгнээний утгыг тоо тус бүрийн 2-р эгнээний утгыг квадрат болгох замаар олж авна. би. Хүснэгтийн сүүлчийн баганын утгууд нь мөр хоорондын утгуудын нийлбэр юм. Коэффициентийг олохын тулд бид хамгийн бага квадратын аргын томъёог ашигладаг аболон б. Бид тэдгээрт хүснэгтийн сүүлчийн баганаас харгалзах утгуудыг орлуулна. Үүний үр дүнд, у=0,165х+2,184нь хүссэн ойролцоох шулуун шугам юм. Энэ мөрүүдийн аль нь болохыг олж мэдэх л үлдлээ у=0,165х+2,184эсвэл Үүнийг хийхийн тулд та эдгээр мөрүүдээс анхны өгөгдлийн квадрат хазайлтын нийлбэрийг тооцоолох хэрэгтэй оноос хойш, дараа нь шугам у=0,165х+2,184анхны өгөгдлийг илүү сайн ойртуулдаг. График дээр бүх зүйл сайхан харагдаж байна. Улаан шугам нь олсон шугам юм у=0,165х+2,184, цэнхэр шугам нь Энэ нь юунд зориулагдсан бэ, энэ бүх ойролцоо тооцоолол юунд зориулагдсан бэ? Би хувьдаа өгөгдлийг тэгшитгэх, интерполяци, экстраполяцийн асуудлыг шийдвэрлэхэд ашигладаг (анхны жишээнд танаас ажиглагдсан утгын утгыг олохыг хүсч болно. yцагт x=3эсвэл хэзээ x=6 MNC аргын дагуу). Гэхдээ бид энэ талаар дараа нь сайтын өөр хэсэгт дэлгэрэнгүй ярих болно. Хуудасны дээд талд Баталгаа. Тиймээс олдсон үед аболон бфункц нь хамгийн бага утгыг авдаг тул энэ үед функцийн хоёр дахь эрэмбийн дифференциалын квадрат хэлбэрийн матриц шаардлагатай. Хоёрдахь эрэмбийн дифференциал нь дараах хэлбэртэй байна. Тэр бол Тиймээс квадрат хэлбэрийн матриц нь хэлбэртэй байна Матриц нь эерэг тодорхой гэдгийг харуулъя. Энэ нь насанд хүрээгүй өнцөг нь эерэг байхыг шаарддаг. Нэгдүгээр эрэмбийн өнцгийн минор Хоёрдахь эрэмбийн өнцгийн минор Үүнийг баталцгаая Дүгнэлт: олсон утгууд аболон бфункцийн хамгийн бага утгатай тохирно Ойлгосон уу? Хуудасны дээд талд Экстраполяци
Энэ бол урьдын болон одоогийн чиг хандлага, хэв маяг, урьдчилан таамаглах объектын ирээдүйн хөгжилд хамаарах харилцааг түгээхэд үндэслэсэн шинжлэх ухааны судалгааны арга юм. Экстраполяцийн аргууд орно
хөдөлж буй дундаж арга, экспоненциал тэгшитгэх арга, хамгийн бага квадратын арга. Мөн чанар хамгийн бага квадратын арга
ажиглагдсан болон тооцоолсон утгуудын хоорондох квадрат хазайлтын нийлбэрийг багасгахаас бүрдэнэ. Тооцоолсон утгыг сонгосон тэгшитгэлийн дагуу олно - регрессийн тэгшитгэл. Бодит болон тооцоолсон утгуудын хоорондох зай бага байх тусам регрессийн тэгшитгэл дээр үндэслэн таамаглал илүү нарийвчлалтай болно. Судалгаанд хамрагдаж буй үзэгдлийн мөн чанар, өөрчлөлтийг цаг хугацааны цуваагаар харуулсан онолын шинжилгээ нь муруйг сонгох үндэс суурь болдог. Цувралын түвшний өсөлтийн шинж чанарын талаархи бодол санааг заримдаа харгалзан үздэг. Тиймээс, хэрэв бүтээгдэхүүний өсөлтийг арифметик прогрессоор хүлээж байгаа бол тэгшитгэх ажлыг шулуун шугамаар гүйцэтгэдэг. Хэрэв өсөлт нь экспоненциал болж хувирвал экспоненциал функцийн дагуу жигдрүүлэх хэрэгтэй. Хамгийн бага квадратын аргын ажлын томьёо
: Y t+1 = a*X + b, энд t + 1 нь таамагласан хугацаа; Уt+1 – таамагласан үзүүлэлт; a ба b коэффициентүүд; X бол цаг хугацааны бэлгэдэл юм. a ба b коэффициентийг дараахь томъёогоор тооцоолно. хаана, Uf - динамикийн цувралын бодит утгууд; n - цаг хугацааны цувралын түвшний тоо; Цагийн цувааг хамгийн бага квадратын аргаар тэгшитгэх нь судалж буй үзэгдлийн хөгжлийн зүй тогтлыг тусгах үүрэгтэй. Трендийн аналитик илэрхийлэлд цагийг бие даасан хувьсагч гэж үздэг бөгөөд цувралын түвшин нь энэхүү бие даасан хувьсагчийн функцээр ажилладаг. Аливаа үзэгдлийн хөгжил нь эхлэлийн цэгээс хойш хэдэн жил өнгөрсөнөөс хамаарахгүй, харин түүний хөгжилд ямар хүчин зүйл нөлөөлсөн, ямар чиглэлд, ямар эрчимтэй явагдсанаас хамаардаг. Үүнээс үзэхэд аливаа үзэгдлийн хөгжил нь эдгээр хүчин зүйлсийн үйл ажиллагааны үр дүнд цаг хугацааны явцад гарч ирдэг. Муруйн хэлбэр, цаг хугацааны аналитик хамаарлын төрлийг зөв тогтоох нь урьдчилан таамаглах шинжилгээний хамгийн хэцүү ажлуудын нэг юм.
. Параметрүүд нь хамгийн бага квадратын аргаар тодорхойлогддог чиг хандлагыг тодорхойлсон функцийн төрлийг сонгох нь ихэнх тохиолдолд эмпирик бөгөөд хэд хэдэн функцийг байгуулж, тэдгээрийг язгуурын утгын хувьд өөр хоорондоо харьцуулах замаар хийгддэг. -томьёогоор тооцоолсон дундаж квадрат алдаа: хаана Uf - динамикийн цувралын бодит утгууд; Ur - хугацааны цувааны тооцоолсон (тэгшгэсэн) утгууд; n - цаг хугацааны цувралын түвшний тоо; p нь чиг хандлагыг (хөгжлийн чиг хандлага) тодорхойлсон томъёонд тодорхойлсон параметрүүдийн тоо юм. Хамгийн бага квадратын аргын сул тал
: Даалгавар
. Бүс нутгийн ажилгүйдлийн түвшинг тодорхойлсон тоо баримт бий, % Хамгийн бага квадратын шийдэл
Шийдлийн хувьд бид шаардлагатай тооцоог хийх хүснэгтийг эмхэтгэх болно. ε = 28.63/10 = 2.86% таамаглалын нарийвчлалөндөр. Дүгнэлт
: Тооцоололд гарсан үр дүнг харьцуулах хөдөлж буй дундаж арга
, экспоненциал тэгшитгэх
ба хамгийн бага квадратын аргын хувьд экспоненциал тэгшитгэх аргын тооцооны дундаж харьцангуй алдаа 20-50% -д хүрдэг гэж хэлж болно. Энэ нь энэ тохиолдолд таамаглалын нарийвчлал нь зөвхөн хангалттай гэсэн үг юм. Эхний болон гурав дахь тохиолдолд дундаж харьцангуй алдаа 10% -иас бага байдаг тул таамаглалын нарийвчлал өндөр байна. Гэхдээ хөдөлж буй дундаж арга нь илүү найдвартай үр дүнд хүрэх боломжийг олгосон (11-р сарын таамаглал - 1.52%, 12-р сарын урьдчилсан мэдээ - 1.53%, 1-р сарын урьдчилсан мэдээ - 1.49%), учир нь энэ аргыг ашиглах үед харьцангуй дундаж алдаа хамгийн бага байдаг - 1. ,13%. Ашигласан эх сурвалжуудын жагсаалт би- туршилтын цэгийн дугаар; График дээр дарна уу Өгөгдлийн талбарт тусдаа мөр бүрт нэг туршилтын цэг дээр `x` ба `y` утгуудыг оруулна. Утга нь хоосон зайгаар (зай эсвэл таб) тусгаарлагдсан байх ёстой. Гурав дахь утга нь `w` цэгийн жин байж болно. Хэрэв цэгийн жинг заагаагүй бол энэ нь нэгтэй тэнцүү байна. Ихэнх тохиолдолд туршилтын цэгүүдийн жин тодорхойгүй эсвэл тооцоологдоогүй; туршилтын бүх өгөгдлийг тэнцүү гэж үзнэ. Заримдаа судлагдсан утгын хүрээн дэх жин нь мэдээж тэнцүү биш бөгөөд онолын хувьд ч тооцоолж болно. Жишээлбэл, спектрофотометрийн хувьд жинг энгийн томъёогоор тооцоолж болох боловч үндсэндээ хүн бүр хөдөлмөрийн зардлыг бууруулахын тулд үүнийг үл тоомсорлодог. Microsoft Office-ийн Excel эсвэл Open Office-ийн Calc гэх мэт оффисын багцын хүснэгтээс өгөгдлийг санах ойд буулгаж болно. Үүнийг хийхийн тулд хүснэгтээс хуулах өгөгдлийн хүрээг сонгоод санах ой руу хуулж, энэ хуудасны өгөгдлийн талбарт өгөгдлийг буулгана уу. Хамгийн бага квадратын аргаар тооцоолохын тулд хоёр коэффициентийг тодорхойлохын тулд дор хаяж хоёр цэг шаардлагатай `b` - шулуун шугамын налуу өнцгийн тангенс ба `a` - `y дээрх шулуун шугамаар таслагдсан утга. ` тэнхлэг. Тооцоолсон регрессийн коэффициентүүдийн алдааг тооцоолохын тулд туршилтын цэгүүдийн тоог хоёроос дээш болгох шаардлагатай. Туршилтын цэгүүдийн тоо их байх тусам коэффициентүүдийн статистик тооцоолол (Оюутны коэффициент буурсантай холбоотой) илүү нарийвчлалтай, ерөнхий түүврийн тооцоонд ойртох болно. Туршилтын цэг бүрт үнэ цэнийг олж авах нь ихэвчлэн их хэмжээний хөдөлмөрийн зардалтай холбоотой байдаг тул олон тооны туршилтуудыг ихэвчлэн хийдэг бөгөөд энэ нь шингэцтэй тооцооллыг өгдөг бөгөөд хэт их хөдөлмөрийн зардалд хүргэдэггүй. Дүрмээр бол хоёр коэффициент бүхий шугаман хамгийн бага квадратын хамаарлын туршилтын цэгүүдийн тоог 5-7 цэгийн бүсэд сонгоно. Бидэнд хос утгын [`y_i`, `x_i`] хэлбэрийн туршилтын өгөгдлийн багц байна гэж бодъё, энд `i` нь 1-ээс `n` хүртэлх туршилтын нэг хэмжилтийн тоо юм; `y_i` - `i` цэг дэх хэмжсэн утгын утга; `x_i` - `i` цэг дээр бидний тогтоосон параметрийн утга. Жишээ нь Ом хуулийн үйл ажиллагаа юм. Цахилгаан хэлхээний хэсгүүдийн хоорондох хүчдэлийг (боломжийн зөрүү) өөрчилснөөр бид энэ хэсгийг дамжин өнгөрөх гүйдлийн хэмжээг хэмждэг. Физик бидэнд туршилтаар олсон хамаарлыг өгдөг. `I=U/R`, Энэ тохиолдолд `y_i` нь хэмжсэн гүйдлийн утга, `x_i` нь хүчдэлийн утга юм. Өөр нэг жишээ болгон, уусмал дахь бодисын уусмал гэрлийн шингээлтийг авч үзье. Хими бидэнд дараах томъёог өгдөг. `A = εl C`, Энэ тохиолдолд 'y_i' нь хэмжсэн оптик нягт 'A', 'x_i' нь бидний тогтоосон бодисын концентрац юм. `x_i`-г тохируулах харьцангуй алдаа нь `y_i`-г хэмжих харьцангуй алдаанаас хамаагүй бага байх тохиолдлыг бид авч үзэх болно. Бид мөн 'y_i' хэмжсэн бүх утгууд нь санамсаргүй бөгөөд хэвийн тархалттай байна, өөрөөр хэлбэл. хэвийн тархалтын хуулийг дагаж мөрдөх. `y`-ийн `x`-ээс шугаман хамаарлын хувьд онолын хамаарлыг дараах байдлаар бичиж болно. Геометрийн үүднээс авч үзвэл `b` коэффициент нь шугамын налуугийн `x` тэнхлэгт хүрэх шүргэгчийг, `a` коэффициент нь шугамын `-тэй огтлолцох цэг дэх `y` утгыг илэрхийлнэ. y` тэнхлэг (`x = 0`-тай). Туршилтын хувьд хэмжилтийн алдаанаас болж 'y_i' хэмжсэн утгууд нь бодит амьдрал дээр үргэлж байдаг тул онолын шугам дээр яг таарч чадахгүй. Тиймээс шугаман тэгшитгэлийг тэгшитгэлийн системээр илэрхийлэх ёстой. Хамаарал (1) гэж бас нэрлэдэг регресс, өөрөөр хэлбэл статистикийн ач холбогдол бүхий хоёр хэмжигдэхүүн бие биенээсээ хамаарах хамаарал. Хараат байдлыг сэргээх ажил нь туршилтын цэгүүдээс [`y_i`, `x_i`] `a` ба `b` коэффициентүүдийг олох явдал юм. "a" ба "b" коэффициентийг олохын тулд ихэвчлэн ашигладаг хамгийн бага квадрат арга(MNK). Энэ нь хамгийн их магадлалын зарчмын онцгой тохиолдол юм. (1)-ийг `ε_i = y_i - a - b x_i` гэж дахин бичье. Дараа нь квадрат алдааны нийлбэр болно Хамгийн бага квадратын аргын зарчим нь `a` ба `b` параметрүүдийн нийлбэрийг (2) багасгах явдал юм.. `a` ба `b` коэффициентүүдийн нийлбэрийн (2) хэсэгчилсэн деривативууд тэгтэй тэнцүү байх үед хамгийн багадаа хүрнэ. Деривативуудыг өргөжүүлснээр бид хоёр үл мэдэгдэх хоёр тэгшитгэлийн системийг олж авна. Бид хаалтуудыг нээж, хүссэн коэффициентээс хамааралгүй нийлбэрүүдийг нөгөө хагаст шилжүүлж, шугаман тэгшитгэлийн системийг олж авна. Үүссэн системийг шийдэж, бид "a" ба "b" коэффициентүүдийн томъёог олно. `a = фрак(нийлбэр_(i=1)^(n) y_i нийлбэр_(i=1)^(n) x_i^2 - нийлбэр_(i=1)^(n) x_i нийлбэр_(i=1)^(n) ) x_iy_i) (n нийлбэр_(i=1)^(n) x_i^2 — (нийлбэр_(i=1)^(n) x_i)^2)` (3.1) `b = фрак(n нийлбэр_(i=1)^(n) x_iy_i - нийлбэр_(i=1)^(n) x_i нийлбэр_(i=1)^(n) y_i) (n нийлбэр_(i=1)^ (n) x_i^2 - (нийлбэр_(i=1)^(n) x_i)^2)` (3.2) Эдгээр томьёо нь `n > 1` (дор хаяж 2 цэг ашиглан шугамыг зурж болно) болон тодорхойлогч `D = n нийлбэр_(i=1)^(n) x_i^2 — (нийлбэр_(i= 1) үед шийдлүүдтэй байна. )^(n) x_i)^2 != 0`, i.e. Туршилтын `x_i` цэгүүд өөр байх үед (жишээ нь шугам босоо биш үед). `a` ба `b` коэффициентүүдийг тооцоолоход гарсан алдааг илүү нарийвчлалтай тооцоолохын тулд олон тооны туршилтын цэгүүдийг авах нь зүйтэй. `n = 2` үед коэффициентүүдийн алдааг тооцоолох боломжгүй, учир нь Ойролцоо шугам нь хоёр цэгээр давтагдашгүй өнгөрнө. `V` санамсаргүй хэмжигдэхүүний алдаа тодорхойлогдоно алдааны хуримтлалын хууль `a` ба `b` коэффициентүүдийн алдааны алдааны хуримтлалын хуулийг бичье. `S_y^2 = S_(y_i)^2` - `y` хэмжигдэхүүн дэх алдаа (дисвэр, квадрат стандарт хазайлт), алдааг бүх `y` утгуудын хувьд жигд байна гэж үзвэл. Үр дүнгийн илэрхийлэлд "a" ба "b"-ийг тооцоолох томъёог орлуулснаар бид олж авна. `S_a^2 = S_y^2 фрак(нийлбэр_(i=1)^(n) (нийлбэр_(i=1)^(n) x_i^2 - x_i нийлбэр_(i=1)^(n) x_i)^2 ) (D^2) = S_y^2 фрак((n нийлбэр_(i=1)^(n) x_i^2 - (нийлбэр_(i=1)^(n) x_i)^2) нийлбэр_(i=1) ^(n) x_i^2) (D^2) = S_y^2 фрак(нийлбэр_(i=1)^(n) x_i^2) (D)` (4.1) `S_b^2 = S_y^2 фрак(нийлбэр_(и=1)^(n) (n x_i - нийлбэр_(i=1)^(n) x_i)^2) (D^2) = S_y^2 фрак( n (n нийлбэр_(i=1)^(n) x_i^2 - (нийлбэр_(i=1)^(n) x_i)^2)) (D^2) = S_y^2 фрак(n) (D) ` (4.2) Ихэнх бодит туршилтуудад `Sy`-ийн утгыг хэмждэггүй. Үүнийг хийхийн тулд төлөвлөгөөний нэг буюу хэд хэдэн цэг дээр хэд хэдэн зэрэгцээ хэмжилт (туршилт) хийх шаардлагатай бөгөөд энэ нь туршилтын хугацааг (болон магадгүй зардал) нэмэгдүүлдэг. Тиймээс регрессийн шугамаас `y`-ийн хазайлтыг санамсаргүй гэж үзэж болно гэж ихэвчлэн үздэг. Энэ тохиолдолд 'y' хэлбэлзлийн үнэлгээг томъёогоор тооцоолно. `S_y^2 = S_(y, амралт)^2 = фрак(нийлбэр_(i=1)^n (y_i - a - b x_i)^2) (n-2)`. Туршилтын ижил түүврийн өгөгдлийн хоёр коэффициентийг тооцоолсны улмаас бид эрх чөлөөний зэрэглэлийн тоог бууруулсан тул хуваагч `n-2` гарч ирнэ. Энэ тооцоог мөн `S_(y, амралт)^2` регрессийн шугамтай харьцуулахад үлдэгдэл дисперс гэж нэрлэдэг. Коэффициентийн ач холбогдлын үнэлгээг оюутны шалгуурын дагуу гүйцэтгэдэг `t_a = frac(|a|) (S_a)`, `t_b = frac(|b|) (S_b)` Хэрэв тооцоолсон `t_a`, `t_b` шалгуур үзүүлэлтүүд нь `t(P, n-2)` хүснэгтийн шалгуураас бага байвал харгалзах коэффициент нь өгөгдсөн `P` магадлалаар тэгээс мэдэгдэхүйц ялгаатай биш гэж үзнэ. Шугаман харилцааны тайлбарын чанарыг үнэлэхийн тулд та Фишерийн шалгуурыг ашиглан `S_(y, амралт)^2` ба `S_(bar y)`-ийг дундажтай харьцуулж болно. `S_(бар y) = фрак(нийлбэр_(i=1)^n (y_i - багана у)^2) (n-1) = фрак(нийлбэр_(i=1)^n (y_i - (нийлбэр_(i=) 1)^n y_i) /n)^2) (n-1)` - дундажтай харьцуулахад `y`-ийн дисперсийн түүврийн тооцоо. Хамааралтай байдлыг тодорхойлох регрессийн тэгшитгэлийн үр нөлөөг үнэлэхийн тулд Фишерийн коэффициентийг тооцоолно. Хэрэв `F > F(P, n-1, n-2)` бол `y = f(x)` хамаарлыг регрессийн тэгшитгэл ашиглан тайлбарлах ба дундаж утгыг ашигласан тайлбарын хоорондох зөрүүг магадлалын хувьд статистикийн хувьд ач холбогдолтой гэж үзнэ. `P`. Тэдгээр. регресс нь дундаж утгын эргэн тойронд "y"-ийн тархалтаас илүү хамааралтай байдлыг илүү сайн тодорхойлдог. График дээр дарна уу Хамгийн бага квадратын арга нь үл мэдэгдэх параметрүүдийг тодорхойлох гэсэн үг юм a, b, c,…хүлээн зөвшөөрөгдсөн функциональ хамаарал у = f(x,a,b,c,…), Энэ нь алдааны дундаж квадратын (дисвэрийн) хамгийн бага хэмжээг өгөх болно Энд x i , y i - туршилтаас олж авсан хос тоонуудын багц. Хэд хэдэн хувьсагчийн функцийн экстремумын нөхцөл нь түүний хэсэгчилсэн дериватив нь тэгтэй тэнцүү байх нөхцөл байдаг тул параметрүүд нь a, b, c,…тэгшитгэлийн системээр тодорхойлогддог. ; ; ; … (25) Функцийн хэлбэрийн дараа параметрүүдийг сонгохдоо хамгийн бага квадратын аргыг ашигладаг гэдгийг санах нь зүйтэй у = f(x)тодорхойлсон. Хэрэв онолын үүднээс авч үзвэл эмпирик томъёо нь ямар байх ёстой талаар ямар нэгэн дүгнэлт хийх боломжгүй бол харааны дүрслэл, юуны түрүүнд ажиглагдсан өгөгдлийн график дүрслэлийг удирдан чиглүүлэх шаардлагатай. Практикт ихэвчлэн дараахь төрлийн функцээр хязгаарлагддаг. 1) шугаман 2) квадрат a .
Оршил
Дериватив гэж юу болохыг та мэдэх үү? Ялгаатай харьцааны хязгаарыг та надад хэлэх байх. Санкт-Петербургийн Улсын Их Сургуулийн математикийн нэгдүгээр курст Виктор Петрович Хавин намайг тодорхойлсонцэг дэх функцийн Тейлорын цувралын эхний гишүүний коэффициент гэж дериватив (энэ нь деривативгүйгээр Тейлорын цувралыг тодорхойлох тусдаа гимнастик байсан). Энэ тодорхойлолтыг би эцэст нь юу болохыг ойлгох хүртлээ удаан хугацаанд инээв. Дериватив гэдэг нь бидний ялгаж буй функц y=x, y=x^2, y=x^3 функцтэй хэр зэрэг төстэй болохыг харуулах хэмжүүрээс өөр зүйл биш юм.Квадрат хэлбэрийн хамгийн бага
Тиймээс векторыг өгсөн бматрицын багана-векторуудаар дамжсан хавтгай А(энэ тохиолдолд (x0,x1,x2) ба (1,1,1)) бид векторыг хайж байна. дхамгийн бага квадрат урттай. Мэдээжийн хэрэг, хамгийн багадаа зөвхөн векторын хувьд хүрэх боломжтой д, матрицын багана-векторуудаар дамжсан хавтгайд ортогональ А:Дирихлегийн хилийн нөхцөлтэй Лапласын тэгшитгэл
Одоо хамгийн энгийн бодит асуудал: тодорхой гурвалжин гадаргуу байгаа тул үүнийг тэгшлэх шаардлагатай. Жишээлбэл, миний нүүрний загварыг ачаалъя:
nlКоэффицент(нүүр[ j ], 2); nlКоэффицент(нүүр[(j+1)%3], -2);Пуассоны тэгшитгэл
Өөр нэг сайхан нэртэй болцгооё. 
Хамгийн бага квадратын аргын мөн чанар (LSM).
хамгийн бага утгыг авдаг. Энэ нь өгөгдлийг өгсөн гэсэн үг юм аболон болсон шулуун шугамаас туршилтын өгөгдлийн квадрат хазайлтын нийлбэр хамгийн бага байх болно. Энэ бол хамгийн бага квадратын аргын бүх санаа юм.Коэффициент олох томьёо гарган авах.
хувьсагчаар аболон б, бид эдгээр деривативуудыг тэгтэй тэнцүүлж байна. 
хамгийн бага утгыг авдаг. Энэ баримтыг нотлох баримтыг өгсөн болно хуудасны төгсгөлд байгаа текстийн доор.
анхны өгөгдөлд илүү ойртох, өөрөөр хэлбэл хамгийн бага квадратын аргыг ашиглан тооцоолол хийх.Хамгийн бага квадратын аргын алдааны тооцоо.
болон 
, жижиг утга нь хамгийн бага квадратын аргын хувьд анхны өгөгдөлд илүү сайн ойртсон шугамтай тохирч байна. 
Хамгийн бага квадратын аргын (LSM) график дүрслэл.
, ягаан цэгүүд нь анхны өгөгдөл юм.
, 
, энэ нь өгөгдсөн функцийн язгуурын квадратын ойролцооллыг цэгүүдийн хувьд гүйцэтгэдэг. Функц зохиох 
шаардлагатай экстремум нөхцөлийг бичнэ үү:
Хамгийн бага квадратын аргын мөн чанар (LSM).
хамгийн бага утгыг авдаг. Энэ нь өгөгдлийг өгсөн гэсэн үг юм аболон болсон шулуун шугамаас туршилтын өгөгдлийн квадрат хазайлтын нийлбэр хамгийн бага байх болно. Энэ бол хамгийн бага квадратын аргын бүх санаа юм.Коэффициент олох томьёо гарган авах.
хувьсагчаар аболон б, бид эдгээр деривативуудыг тэгтэй тэнцүүлж байна. 
хамгийн бага утгыг авдаг. Энэ баримтын нотолгоог хуудасны төгсгөлд байгаа текстэнд доор харуулав.
анхны өгөгдөлд илүү ойртох, өөрөөр хэлбэл хамгийн бага квадратын аргыг ашиглан тооцоолол хийх.Хамгийн бага квадратын аргын алдааны тооцоо.
болон 
, жижиг утга нь хамгийн бага квадратын аргын хувьд анхны өгөгдөлд илүү сайн ойртсон шугамтай тохирч байна. 
Хамгийн бага квадратын аргын (LSM) график дүрслэл.
, ягаан цэгүүд нь анхны өгөгдөл юм.
эерэг тодорхой байсан. Үүнийг үзүүлье.
мөн элементүүдийн утга нь үүнээс хамаардаггүй аболон б.
. Оноонууд нь давхцдаггүй тул тэгш бус байдал нь хатуу байна. Үүнийг дараах зүйлд тусгасан болно.
Математик индукцийн арга.
, тиймээс хамгийн бага квадратын аргын хүссэн параметрүүд юм.
Шийдэл захиалахХамгийн бага квадратын аргыг ашиглан таамаглал боловсруулах. Асуудлыг шийдэх жишээ
Прогноз боловсруулахдаа хамгийн бага квадратын аргыг ашиглах жишээ
Хамгийн бага квадрат арга
Бусад холбогдох нийтлэлүүд:
БОЯ хөтөлбөр
Өгөгдлийг оруулна уу
Өгөгдөл ба ойролцоогоор y = a + b x
x i- цэг дээрх тогтмол параметрийн утга би;
y i- цэг дээрх хэмжсэн параметрийн утга би;
ω i- цэг дээрх жинг хэмжих би;
y i, тооцоолол.- хэмжсэн утга ба регрессээс тооцсон утгын зөрүү yцэг дээр би;
S x i (x i)- алдааны тооцоо x iхэмжих үед yцэг дээр би.Өгөгдөл ба ойролцоогоор y = kx
би
x i
y i
ω i
y i, тооцоолол.
Δy би
S x i (x i)
MNC онлайн програмын хэрэглэгчийн гарын авлага.
Хамгийн бага квадратын арга (LSM).
Шугаман хамаарлын хамгийн бага квадратуудын товч онол
хаана `I` - одоогийн хүч; `R` - эсэргүүцэл; `U` - хүчдэл.
Энд `A` нь уусмалын оптик нягт; `ε` - ууссан бодисын дамжуулалт; `l` - уусмал бүхий кюветтээр гэрэл өнгөрөх үед замын урт; `C` нь ууссан бодисын концентраци юм.
`y = a + bx`.Регрессийн шугамын параметрүүдийг олох.
`y_i = a + b x_i + ε_i` (1),
Энд 'ε_i' нь 'i' туршилтын 'y' хэмжилтийн үл мэдэгдэх алдаа юм.
`Φ = нийлбэр_(i=1)^(n) ε_i^2 = нийлбэр_(i=1)^(n) (y_i - a - b x_i)^2`. (2)
`frac(хэсэгчилсэн Φ)(хэсэг a) = frac(хэсэгчилсэн нийлбэр_(i=1)^(n) (y_i - a - b x_i)^2)(хэсэг a) = 0`
`frac(хэсэгчилсэн Φ)(хэсэг b) = frac(хэсэгчилсэн нийлбэр_(i=1)^(n) (y_i - a - b x_i)^2)(хэсэг b) = 0`
`нийлбэр_(i=1)^(n) (2a + 2bx_i - 2y_i) = нийлбэр_(i=1)^(n) (a + bx_i - y_i) = 0`
`нийлбэр_(i=1)^(n) (2bx_i^2 + 2ax_i - 2x_iy_i) = нийлбэр_(i=1)^(n) (bx_i^2 + ax_i - x_iy_i) = 0`
`нийлбэр_(i=1)^(n) y_i = a n + b нийлбэр_(i=1)^(n) bx_i`
`нийлбэр_(i=1)^(n) x_iy_i = a нийлбэр_(i=1)^(n) x_i + b нийлбэр_(i=1)^(n) x_i^2`Регрессийн шугамын коэффициентүүдийн алдааны тооцоо
`S_V^2 = нийлбэр_(i=1)^p (фрак(хэсэг f)(хэсэг z_i))^2 S_(z_i)^2`,
Энд `p` нь `S_V` алдаанд нөлөөлөх `S_(z_i)` алдаатай `z_i` параметрийн тоо;
`f` нь `V`-ийн `z_i`-д хамаарах хамаарлын функц юм.
`S_a^2 = нийлбэр_(i=1)^(n)(фрак(хэсэг а)(хэсэг y_i))^2 S_(y_i)^2 + нийлбэр_(i=1)^(n)(фрак(хэсэг а) )(хэсэгчилсэн x_i))^2 S_(x_i)^2 = S_y^2 нийлбэр_(i=1)^(n)(frac(хэсэг а)(хэсэг y_i))^2 `,
`S_b^2 = нийлбэр_(i=1)^(n)(фрак(хэсэг b)(хэсэг y_i))^2 S_(y_i)^2 + нийлбэр_(i=1)^(n)(фрак(хэсэг b) )(хэсэгчилсэн x_i))^2 S_(x_i)^2 = S_y^2 нийлбэр_(i=1)^(n)(frac(хэсэг b)(хэсэг y_i))^2 `,
учир нь `S_(x_i)^2 = 0` (бид өмнө нь `x`-ын алдаа өчүүхэн гэж тэмдэглэсэн).
`F = S_(бар y) / S_(y, амрах)^2`,
Үүнийг хүснэгтийн Фишерийн коэффициент `F(p, n-1, n-2)`-тай харьцуулсан.
хүснэгтэд утгыг нэмэхХамгийн бага квадрат арга. Хамгийн бага квадратын арга гэдэг нь үл мэдэгдэх параметрүүдийг a, b, c, хүлээн зөвшөөрөгдсөн функциональ хамаарлыг тодорхойлохыг хэлнэ.
, (24)
;
