Хүснэгтийн утгууд cos. Тригонометрийн функцууд
Тангенс (tg x) ба котангенс (ctg x)-ийн лавлагаа өгөгдөл. Геометрийн тодорхойлолт, шинж чанар, график, томьёо. Шүргэгч ба котангентын хүснэгт, дериватив, интеграл, цувааны өргөтгөл. Нарийн төвөгтэй хувьсагчаар дамжуулан илэрхийлэл. Гиперболик функцуудтай холболт.
Геометрийн тодорхойлолт

|BD| - А цэг дээр төвлөрсөн тойргийн нумын урт.
α нь радианаар илэрхийлэгдсэн өнцөг юм.
шүргэгч ( tgα) нь тэгш өнцөгт гурвалжны гипотенуз ба хөлийн хоорондох α өнцгөөс хамаарах тригонометрийн функц бөгөөд эсрэг талын хөлийн уртын харьцаатай тэнцүү |BC| зэргэлдээх хөлний урт хүртэл |AB| .
Котангенс ( ctgα) нь тэгш өнцөгт гурвалжны гипотенуз ба хөлийн хоорондох α өнцгөөс хамаарах тригонометрийн функц бөгөөд зэргэлдээх хөлийн уртын харьцаатай тэнцүү |AB| эсрэг талын хөлний урт хүртэл |BC| .
Тангенс
Хаана n- бүхэлд нь.
Барууны уран зохиолд шүргэгчийг дараах байдлаар тэмдэглэсэн байдаг.
.
;
;
.
Шүргэх функцийн график, y = tg x

Котангенс
Хаана n- бүхэлд нь.
Барууны уран зохиолд котангенсыг дараах байдлаар тэмдэглэсэн байдаг.
.
Дараах тэмдэглэгээг мөн баталсан.
;
;
.
Котангенсийн функцийн график, y = ctg x

Тангенс ба котангенсын шинж чанарууд
Үе үе
Функцууд y= tg xба у= ctg xπ үетэй үечилсэн байна.
Паритет
Тангенс ба котангенс функцууд нь сондгой.
Тодорхойлолт ба утгын хүрээ, өсөх, буурах
Тангенс ба котангенс функцууд нь тодорхойлолтын талбартаа тасралтгүй байдаг (тасралтгүй байдлын баталгааг үзнэ үү). Тангенс ба котангентын үндсэн шинж чанарыг хүснэгтэд үзүүлэв ( n- бүхэл тоо).
| у= tg x | у= ctg x | |
| Хамрах хүрээ ба тасралтгүй байдал | ||
| Утгын хүрээ | -∞ < y < +∞ | -∞ < y < +∞ |
| Өгсөж байна | - | |
| Бууж байна | - | |
| Хэт их | - | - |
| Тэг, у= 0 | ||
| У тэнхлэгтэй огтлолцох цэгүүд, x = 0 | у= 0 | - |
Томъёо
Синус ба косинусын илэрхийлэл
;
;
;
;
;
Нийлбэр ба ялгаварын тангенс ба котангенсийн томъёо
Жишээлбэл, бусад томъёог олж авахад хялбар байдаг
Шүргэгчийн бүтээгдэхүүн
Шүргэгчийн нийлбэр ба зөрүүний томъёо
Энэ хүснэгтэд аргументийн зарим утгуудын шүргэгч ба котангентын утгыг харуулав. 
Комплекс тоонуудын илэрхийлэл
Гиперболын функцүүдийн илэрхийлэл
;
;
Дериватив
; .
.
Функцийн х хувьсагчийн хувьд n-р эрэмбийн дериватив:
.
Шүргэгчийн томьёо гарган авах > > > ; котангенсийн хувьд > > >
Интеграл
Цуврал болгон өргөтгөх
X-ийн зэрэглэлийн тангенсийн тэлэлтийг авахын тулд та өргөтгөлийн хэд хэдэн нөхцөлийг авах хэрэгтэй. эрчим хүчний цувралфункцүүдийн хувьд гэм хболон cos xмөн эдгээр олон гишүүнтүүдийг хооронд нь хувааж, . Үүний үр дүнд дараах томъёо гарч ирнэ.
-д.
цагт.
хаана Б н- Бернуллигийн тоо. Тэдгээрийг дахилтын хамаарлаас аль нэгээр нь тодорхойлно.
;
;
хаана.
Эсвэл Лапласын томъёоны дагуу: 
Урвуу функцууд
Урвуу функцуудшүргэгч ба котангенс нь арктангенс ба арккотангенс байна.
Арктангенс, арктг
, хаана n- бүхэлд нь.
Нуман тангенс, arcctg
, хаана n- бүхэлд нь.
Лавлагаа:
И.Н. Бронштейн, К.А. Семендяев, Дээд боловсролын байгууллагын инженер, оюутнуудад зориулсан математикийн гарын авлага, Лан, 2009 он.
Г.Корн, Судлаач, инженерүүдэд зориулсан математикийн гарын авлага, 2012 он.
Синус (), косинус (), тангенс (), котангенс () гэсэн ойлголтууд нь өнцгийн тухай ойлголттой салшгүй холбоотой байдаг. Эдгээрийг эхлээд харахад нарийн төвөгтэй ойлголтууд (олон сургуулийн сурагчдад айдас төрүүлдэг), "чөтгөр зурсан шигээ аймшигтай биш" гэдгийг сайн ойлгохын тулд эхнээс нь эхэлцгээе. мөн өнцгийн тухай ойлголтыг ойлгох.
Өнцгийн тухай ойлголт: радиан, градус
Зургийг харцгаая. Вектор цэгтэй харьцуулахад тодорхой хэмжээгээр "эргэв". Тиймээс анхны байрлалтай харьцуулахад энэ эргэлтийн хэмжүүр нь байх болно булан.
Өнцгийн тухай ойлголтын талаар өөр юу мэдэх хэрэгтэй вэ? Мэдээжийн хэрэг, өнцгийн нэгжүүд!
Геометр ба тригонометрийн аль алинд нь өнцгийг градус болон радианаар хэмжиж болно.
Өнцөг (нэг градус) нь тойргийн хэсэгтэй тэнцүү дугуй нуман дээр тулгуурласан тойргийн төв өнцөг юм. Тиймээс бүх тойрог нь дугуй нумануудын "хэсэг" -ээс бүрдэх буюу тойргийн дүрсэлсэн өнцөг нь тэнцүү байна.

Өөрөөр хэлбэл, дээрх зураг нь тэнцүү өнцгийг харуулж байна, өөрөөр хэлбэл энэ өнцөг нь тойргийн хэмжээтэй дугуй нуман дээр суурилдаг.
Радианаар хэмжигдэх өнцгийг тойргийн радиустай тэнцүү урттай дугуй нуман дээр тулгуурлан тойргийн төв өнцөг гэж нэрлэдэг. За ойлгов уу? Үгүй бол зургийг харцгаая.

Тиймээс, зураг нь радиантай тэнцүү өнцгийг харуулж байна, өөрөөр хэлбэл энэ өнцөг нь тойргийн радиустай тэнцүү дугуй нуман дээр суурилдаг (урт нь урт эсвэл радиустай тэнцүү). урттай тэнцүүнумууд). Тиймээс нумын уртыг дараах томъёогоор тооцоолно.
Радиан дахь төв өнцөг хаана байна.
За, та үүнийг мэдэж байгаа тул тойргоор дүрсэлсэн өнцөг хэдэн радиан агуулж байгааг хариулж чадах уу? Тийм ээ, үүний тулд та тойргийн тойргийн томъёог санах хэрэгтэй. Тэр тэнд байна:
За, одоо энэ хоёр томьёог харьцуулж тойргоор дүрсэлсэн өнцөг тэнцүү болохыг олж мэдье. Өөрөөр хэлбэл градус ба радиан дахь утгыг харьцуулж үзвэл бид үүнийг олж авна. Тус тусад нь, . Таны харж байгаагаар хэмжилтийн нэгж нь контекстээс ихэвчлэн тодорхой байдаг тул "градус"-аас ялгаатай нь "радиан" гэдэг үгийг орхигдуулдаг.
Хэдэн радиантай вэ? Яг зөв!
Авчихсан? Дараа нь урагшаа чангал:
Ямар нэг хүндрэл байна уу? Дараа нь хар хариултууд:
Зөв гурвалжин: синус, косинус, тангенс, өнцгийн котангенс
Тиймээс, өнцгийн тухай ойлголттой болсон. Гэхдээ өнцгийн синус, косинус, тангенс, котангенс гэж юу вэ? Үүнийг олж мэдье. Үүний тулд тэгш өнцөгт гурвалжин бидэнд тусална.

Тэгш өнцөгт гурвалжны талуудыг юу гэж нэрлэдэг вэ? Энэ нь зөв, гипотенуз ба хөл: гипотенуз нь зөв өнцгийн эсрэг талд байрлах тал юм (бидний жишээнд энэ нь тал юм); хөл нь үлдсэн хоёр тал ба (зэргэлдээх зөв өнцөг), үүнээс гадна, хэрэв бид хөлийг өнцгөөр нь авч үзвэл хөл нь зэргэлдээх хөл, харин хөл нь эсрэг талынх юм. Тэгэхээр одоо өнцгийн синус, косинус, тангенс, котангенс гэж юу вэ гэсэн асуултад хариулъя.
Өнцгийн синуснь эсрэг талын (хол) хөлийг гипотенузтай харьцуулсан харьцаа юм.
манай гурвалжинд.
Өнцгийн косинус- энэ нь зэргэлдээх (ойр) хөлний гипотенузын харьцаа юм.
манай гурвалжинд.
Өнцгийн тангенс- энэ нь эсрэг талын (алс) хөлийг зэргэлдээх (ойр) хөлтэй харьцуулсан харьцаа юм.
манай гурвалжинд.
Өнцгийн котангенс- энэ нь зэргэлдээх (ойр) хөлийн эсрэг талын (хол) харьцаа юм.
манай гурвалжинд.
Эдгээр тодорхойлолтууд зайлшгүй шаардлагатай санаж байна! Аль хөлийг юугаар хуваахыг санахад хялбар болгохын тулд та үүнийг тодорхой ойлгох хэрэгтэй шүргэгчболон котангенсзөвхөн хөл нь сууж, гипотенуз нь зөвхөн дотор гарч ирдэг синусболон косинус. Дараа нь та холбоодын гинжин хэлхээг гаргаж ирж болно. Жишээлбэл, энэ нь:
косинус→хүрч→хүрч→зэргэлдээ;
Котангенс → мэдрэгч → зэргэлдээ.
Юуны өмнө гурвалжны талуудын харьцаа болох синус, косинус, тангенс, котангенс нь эдгээр талуудын уртаас (нэг өнцгөөр) хамаардаггүй гэдгийг санах нь зүйтэй. Бүү итгэ? Дараа нь зургийг харж байгаа эсэхийг шалгаарай:

Жишээлбэл, өнцгийн косинусыг авч үзье. Тодорхойлолтоор гурвалжингаас: , гэхдээ бид гурвалжингаас өнцгийн косинусыг тооцоолж болно: . Та харж байна уу, талуудын урт нь өөр боловч нэг өнцгийн косинусын утга ижил байна. Тиймээс синус, косинус, тангенс, котангенсийн утгууд нь зөвхөн өнцгийн хэмжээнээс хамаарна.
Хэрэв та тодорхойлолтыг ойлгож байгаа бол үргэлжлүүлээд засаарай!
Доорх зурагт үзүүлсэн гурвалжны хувьд бид олно.

За, чи авсан уу? Дараа нь өөрөө оролдоод үзээрэй: булангийн хувьд адилхан тооцоол.
Нэгж (тригонометрийн) тойрог
Градус ба радиануудын тухай ойлголтыг бид радиустай тэнцүү тойргийг авч үзсэн. Ийм тойрог гэж нэрлэдэг ганц бие. Энэ нь тригонометрийн судалгаанд маш их хэрэгтэй байдаг. Тиймээс бид энэ талаар бага зэрэг нарийвчлан авч үзэх болно.

Таны харж байгаагаар энэ тойрог нь декартын координатын системд баригдсан. Тойргийн радиус нь нэгтэй тэнцүү, тойргийн төв нь эх цэг дээр байрладаг бол радиус векторын анхны байрлал нь тэнхлэгийн эерэг чиглэлийн дагуу тогтмол байдаг (бидний жишээнд энэ нь радиус юм).
Тойргийн цэг бүр нь тэнхлэгийн дагуух координат ба тэнхлэгийн дагуух координат гэсэн хоёр тоотой тохирч байна. Эдгээр координатын тоо юу вэ? Тэгээд ер нь тэд яригдаж байгаа сэдэвтэй ямар холбоотой вэ? Үүнийг хийхийн тулд тэгш өнцөгт гурвалжны талаар санаарай. Дээрх зураг дээр та бүхэл бүтэн хоёр гурвалжинг харж болно. Гурвалжинг авч үзье. Энэ нь тэнхлэгт перпендикуляр тул тэгш өнцөгт хэлбэртэй байна.
Гурвалжингаас ямар тэнцүү вэ? Яг зөв. Нэмж дурдахад энэ нь нэгж тойргийн радиус гэдгийг бид мэднэ, тиймээс, . Энэ утгыг манай косинусын томъёонд орлуулна уу. Энд юу болох вэ:
Гурвалжингаас юу тэнцүү вэ? За, мэдээжийн хэрэг! Энэ томьёонд радиусын утгыг орлуулаад дараахийг авна.
Тэгэхээр та тойрогт хамаарах цэгийн координат хэд болохыг хэлж чадах уу? За яахав дээ? Хэрэв та үүнийг ойлгож, зүгээр л тоо юм бол? Энэ нь ямар координаттай тохирч байна вэ? За, мэдээжийн хэрэг, координат! Энэ нь ямар координаттай тохирч байна вэ? Зөв шүү, зохицуулаарай! Тиймээс, цэг.

Тэгээд юу тэнцүү ба? Зөв шүү, тангенс ба котангенсийн тохирох тодорхойлолтыг ашиглаад үүнийг авъя, a.
Хэрэв өнцөг нь том бол яах вэ? Жишээлбэл, энэ зурган дээрх шиг:

Юу өөрчлөгдсөн бэ энэ жишээ? Үүнийг олж мэдье. Үүнийг хийхийн тулд бид дахин тэгш өнцөгт гурвалжин руу эргэв. Тэгш өнцөгт гурвалжинг авч үзье: өнцөг (өнцөгтэй зэргэлдээх). Өнцгийн синус, косинус, тангенс, котангенсийн утга хэд вэ? Энэ нь зөв, бид тригонометрийн функцүүдийн холбогдох тодорхойлолтыг дагаж мөрддөг.
Таны харж байгаагаар өнцгийн синусын утга нь координаттай тохирч байна; өнцгийн косинусын утга - координат; ба шүргэгч ба котангенсийн утгууд нь харгалзах харьцаатай байна. Иймээс эдгээр хамаарал нь радиус векторын аливаа эргэлтэд хамаарна.
Радиус векторын анхны байрлал нь тэнхлэгийн эерэг чиглэлийн дагуу байна гэж аль хэдийн дурдсан. Одоогоор бид энэ векторыг цагийн зүүний эсрэг эргүүлсэн боловч цагийн зүүний дагуу эргүүлбэл юу болох вэ? Ер бусын зүйл байхгүй, та бас тодорхой хэмжээний өнцөг авах болно, гэхдээ энэ нь зөвхөн сөрөг байх болно. Тиймээс радиус векторыг цагийн зүүний эсрэг эргүүлэх үед бид олж авна эерэг өнцөг, мөн цагийн зүүний дагуу эргэх үед - сөрөг.
Тэгэхээр, тойргийн эргэн тойронд радиус векторын бүхэл бүтэн эргэлт нь эсвэл гэдгийг бид мэднэ. Радиус векторыг эргүүлэх эсвэл эргүүлэх боломжтой юу? За, мэдээжийн хэрэг та чадна! Тиймээс эхний тохиолдолд радиус вектор нь нэг бүтэн эргэлт хийж, эсвэл байрлал дээр зогсох болно.
Хоёр дахь тохиолдолд, өөрөөр хэлбэл радиус вектор нь гурван бүрэн эргэлт хийж, эсвэл байрлал дээр зогсох болно.
Тиймээс, дээрх жишээнүүдээс бид өөр өөр өнцөг буюу (энэ нь ямар ч бүхэл тоо) нь радиус векторын ижил байрлалтай тохирч байна гэж дүгнэж болно.
Доорх зураг нь өнцгийг харуулж байна. Ижил зураг нь буланд тохирох гэх мэт. Энэ жагсаалтыг тодорхойгүй хугацаагаар үргэлжлүүлж болно. Эдгээр бүх өнцгийг ерөнхий томьёогоор эсвэл (энэ нь бүхэл тоо байна) бичиж болно.

Одоо үндсэн тригонометрийн функцүүдийн тодорхойлолтыг мэдэж, нэгж тойргийг ашиглан утгууд нь юутай тэнцүү вэ гэдэгт хариулахыг хичээгээрэй.
Энд танд туслах нэгж тойрог байна:

Ямар нэг хүндрэл байна уу? Дараа нь ойлгоцгооё. Тиймээс бид үүнийг мэднэ:
Эндээс бид өнцгийн тодорхой хэмжүүрт тохирох цэгүүдийн координатыг тодорхойлно. За, дарааллаар нь эхэлцгээе: өнцөг нь координаттай цэгтэй тохирч байгаа тул:
Байдаггүй;
Цаашилбал, ижил логикийг баримталснаар бид булангууд нь координаттай цэгүүдтэй тохирч байгааг олж мэдэв. Үүнийг мэдсэнээр тригонометрийн функцүүдийн утгыг харгалзах цэгүүдэд тодорхойлоход хялбар байдаг. Эхлээд өөрөө оролдоод үз, дараа нь хариултуудыг шалгана уу.
Хариултууд:
Байдаггүй
Байдаггүй
Байдаггүй
Байдаггүй
Тиймээс бид дараах хүснэгтийг хийж болно.

Энэ бүх үнэт зүйлсийг санах шаардлагагүй. Нэгж тойрог дээрх цэгүүдийн координат ба тригонометрийн функцүүдийн утгуудын хоорондын захидал харилцааг санахад хангалттай.
Гэхдээ доорхи хүснэгтэд өгөгдсөн өнцгийн тригонометрийн функцүүдийн утгууд, санаж байх ёстой:

Бүү ай, одоо бид жишээнүүдийн аль нэгийг үзүүлэх болно харгалзах утгуудыг энгийн цээжлэх:
Энэ аргыг ашиглахын тулд синусын утгыг бүх хүнд санаж байх нь чухал юм гурван арга хэмжээөнцөг (), түүнчлэн өнцгийн тангенсийн утга. Эдгээр утгыг мэдсэнээр хүснэгтийг бүхэлд нь сэргээхэд хялбар байдаг - косинусын утгуудыг сумны дагуу шилжүүлдэг, өөрөөр хэлбэл:
Үүнийг мэдсэнээр та утгыг сэргээх боломжтой. Тоолуур " " таарч, хуваагч " " таарна. Котангентын утгыг зурагт үзүүлсэн сумны дагуу шилжүүлнэ. Хэрэв та үүнийг ойлгож, диаграммыг сумаар санаж байвал хүснэгтээс бүх утгыг санахад хангалттай байх болно.
Тойрог дээрх цэгийн координатууд
Тойрог дээрх цэгийг (түүний координатыг) олох боломжтой юу? тойргийн төвийн координат, түүний радиус, эргэлтийн өнцгийг мэдэх?
За, мэдээжийн хэрэг та чадна! Гаргаад ирье ерөнхий томъёоцэгийн координатыг олох.
Жишээлбэл, энд ийм тойрог байна:

Цэг нь тойргийн төв гэдгийг бидэнд өгсөн. Тойргийн радиус тэнцүү байна. Цэгийг градусаар эргүүлэх замаар олж авсан цэгийн координатыг олох шаардлагатай.
Зургаас харахад цэгийн координат нь сегментийн урттай тохирч байна. Сегментийн урт нь тойргийн төвийн координаттай тохирч, өөрөөр хэлбэл тэнцүү байна. Косинусын тодорхойлолтыг ашиглан сегментийн уртыг илэрхийлж болно.
Дараа нь бид цэгийн координатыг авна.
Үүнтэй ижил логикоор бид цэгийн y координатын утгыг олно. Энэ замаар,
Тиймээс дотор ерөнхий үзэлцэгийн координатыг дараах томъёогоор тодорхойлно.
Тойргийн төвийн координат,
тойрог радиус,
Радиус векторын эргэлтийн өнцөг.
Таны харж байгаагаар бидний авч үзэж буй нэгж тойргийн хувьд төвийн координат нь тэг, радиус нь нэгтэй тэнцүү тул эдгээр томьёо нь мэдэгдэхүйц буурсан байна.
За, тойрог дээрх цэгүүдийг олох дасгал хийж, амтлахын тулд эдгээр томъёог туршиж үзье?
1. Нэг цэгийг эргүүлснээр олж авсан нэгж тойрог дээрх цэгийн координатыг ол.
2. Нэг цэгийг эргүүлснээр олж авсан нэгж тойрог дээрх цэгийн координатыг ол.
3. Нэг цэгийг эргүүлснээр олж авсан нэгж тойрог дээрх цэгийн координатыг ол.
4. Цэг - тойргийн төв. Тойргийн радиус тэнцүү байна. Эхний радиус векторыг эргүүлснээр олж авсан цэгийн координатыг олох шаардлагатай.
5. Цэг - тойргийн төв. Тойргийн радиус тэнцүү байна. Эхний радиус векторыг эргүүлснээр олж авсан цэгийн координатыг олох шаардлагатай.
Тойрог дээрх цэгийн координатыг олоход бэрхшээлтэй байна уу?
Эдгээр таван жишээг шийдээрэй (эсвэл шийдлийг сайн ойлгоорой), та тэдгээрийг хэрхэн олохыг сурах болно!
1.
Үүнийг харж болно. Мөн бид эхлэлийн цэгийг бүрэн эргүүлэхэд юу тохирохыг бид мэднэ. Тиймээс хүссэн цэг нь эргэх үед ижил байрлалд байх болно. Үүнийг мэдсэнээр бид цэгийн хүссэн координатыг олно.
2. Тойрог нь нэг цэгийн төвтэй нэгж бөгөөд энэ нь бид хялбаршуулсан томъёог ашиглаж болно гэсэн үг юм:
Үүнийг харж болно. Эхлэх цэгийн хоёр бүрэн эргэлтэнд юу тохирохыг бид мэднэ. Тиймээс хүссэн цэг нь эргэх үед ижил байрлалд байх болно. Үүнийг мэдсэнээр бид цэгийн хүссэн координатыг олно.
Синус ба косинус нь хүснэгтийн утгууд юм. Бид тэдний үнэ цэнийг санаж, дараахь зүйлийг авна.
Тиймээс хүссэн цэг нь координаттай байна.
3. Тойрог нь нэг цэгийн төвтэй нэгж бөгөөд энэ нь бид хялбаршуулсан томъёог ашиглаж болно гэсэн үг юм:
Үүнийг харж болно. Зураг дээр авч үзсэн жишээг дүрсэлцгээе.

Радиус нь тэнхлэгтэй тэнцүү өнцөг үүсгэдэг. Косинус ба синусын хүснэгтийн утгууд тэнцүү гэдгийг мэдэж, энд косинус авдаг болохыг тогтоов сөрөг утгатай, мөн синус эерэг байвал бидэнд:
Сэдвийн тригонометрийн функцийг багасгах томъёог судлахдаа ижил төстэй жишээнүүдийг илүү нарийвчлан шинжилдэг.
Тиймээс хүссэн цэг нь координаттай байна.
4.
Радиус векторын эргэлтийн өнцөг (нөхцөлөөр)
Синус ба косинусын харгалзах тэмдгүүдийг тодорхойлохын тулд бид нэгж тойрог ба өнцгийг байгуулна.

Таны харж байгаагаар үнэ цэнэ нь эерэг, утга нь сөрөг байна. Харгалзах тригонометрийн функцүүдийн хүснэгтийн утгыг мэдсэнээр бид дараахь зүйлийг олж авна.
Хүлээн авсан утгыг томъёонд орлуулж, координатыг олъё.
Тиймээс хүссэн цэг нь координаттай байна.
5. Энэ асуудлыг шийдэхийн тулд бид томъёог ерөнхий хэлбэрээр ашигладаг, хаана
Тойргийн төвийн координатууд (бидний жишээнд,
Тойргийн радиус (нөхцөлөөр)
Радиус векторын эргэлтийн өнцөг (нөхцөлөөр).
Томъёонд бүх утгыг орлуулаад дараахийг авна уу:
ба - хүснэгтийн утгууд. Бид тэдгээрийг санаж, томъёонд орлуулна:
Тиймээс хүссэн цэг нь координаттай байна.
ХУРААНГУЙ БА ҮНДСЭН ТОМЪЁО
Өнцгийн синус нь эсрэг талын (алс) хөлийг гипотенузтай харьцуулсан харьцаа юм.
Өнцгийн косинус нь зэргэлдээх (ойр) хөлийг гипотенузтай харьцуулсан харьцаа юм.
Өнцгийн тангенс нь эсрэг талын (алс) хөлийг зэргэлдээх (ойр) хөлтэй харьцуулсан харьцаа юм.
Өнцгийн котангенс нь зэргэлдээх (ойр) хөлийн эсрэг талын (хол) харьцаа юм.
Өгүүлэлд бид ямар харагдахыг бүрэн ойлгох болно ширээ тригонометрийн утгууд, синус, косинус, тангенс ба котангенс. Тригонометрийн функцүүдийн үндсэн утгыг 0,30,45,60,90,...,360 градусын өнцгөөс авч үзье. Тригонометрийн функцүүдийн утгыг тооцоолохдоо эдгээр хүснэгтийг хэрхэн ашиглахыг харцгаая.
Эхлээд бодож үзээрэй косинус, синус, тангенс, котангенсийн хүснэгт 0, 30, 45, 60, 90,.. градусын өнцгөөс. Эдгээр хэмжигдэхүүнүүдийн тодорхойлолт нь 0 ба 90 градусын өнцгийн функцүүдийн утгыг тодорхойлох боломжийг олгодог.
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, 00-ийн котангенс тодорхойгүй болно
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0-ийн тангенс тодорхойгүй болно
Хэрэв та авбал зөв гурвалжин 30-аас 90 градусын өнцөг. Бид авах:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Бид олж авсан бүх утгыг маягтаар илэрхийлдэг тригонометрийн хүснэгт:
Синус, косинус, тангенс, котангентын хүснэгт!
Хэрэв бид цутгамал томъёог ашиглавал хүснэгт маань нэмэгдэж, 360 градус хүртэлх өнцгийн утгууд нэмэгдэх болно. Энэ нь дараах байдлаар харагдах болно.

Мөн үелэх шинж чанарт үндэслэн z нь бүхэл тоо болох 0 0 +360 0 *z .... 330 0 +360 0 *z өнцгүүдийг орлуулж чадвал хүснэгтийг нэмэгдүүлж болно. Энэ хүснэгтэд нэг тойрог дахь цэгүүдэд тохирох бүх өнцгийн утгыг тооцоолох боломжтой.

Шийдэл дэх хүснэгтийг хэрхэн ашиглахыг тодорхой харцгаая.
Бүх зүйл маш энгийн. Учир нь бидэнд хэрэгтэй үнэ цэнэ нь бидэнд хэрэгтэй нүднүүдийн огтлолцлын цэг дээр байрладаг. Жишээлбэл, 60 градусын өнцгийн cos-ийг авч үзье, хүснэгтэд энэ нь дараах байдалтай байна.

Тригонометрийн функцүүдийн үндсэн утгуудын эцсийн хүснэгтэд бид ижил аргаар ажилладаг. Гэхдээ энэ хүснэгтээс 1020 градусын өнцгөөс шүргэгч хэр их болохыг олж мэдэх боломжтой, энэ нь = -√3 1020 0 = 300 0 +360 0 *2 гэдгийг шалгая. Хүснэгтийг олцгооё.

Брадисын ширээ. Синус, косинус, тангенс, котангенсийн хувьд.
Брэдисийн хүснэгтүүд нь хэд хэдэн хэсэгт хуваагддаг бөгөөд тэдгээр нь косинус ба синус, тангенс ба котангенсийн хүснэгтүүдээс бүрддэг бөгөөд энэ нь хоёр хэсэгт хуваагддаг (90 градус хүртэлх өнцгийн tg ба жижиг өнцгийн ctg).
Синус ба косинус


өнцөг tg 00-ээс 760 хүртэл, өнцөг ctg 140-900 хүртэл.
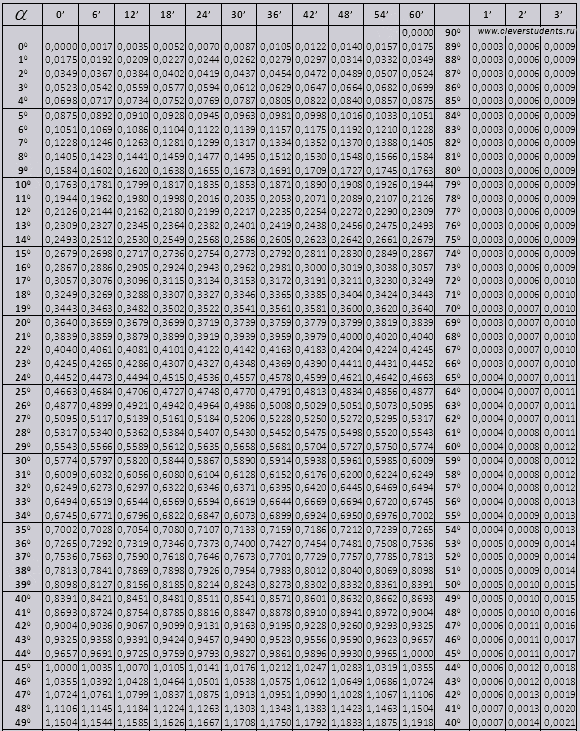

tg хүртэл 900 ба ctg жижиг өнцөгтэй.
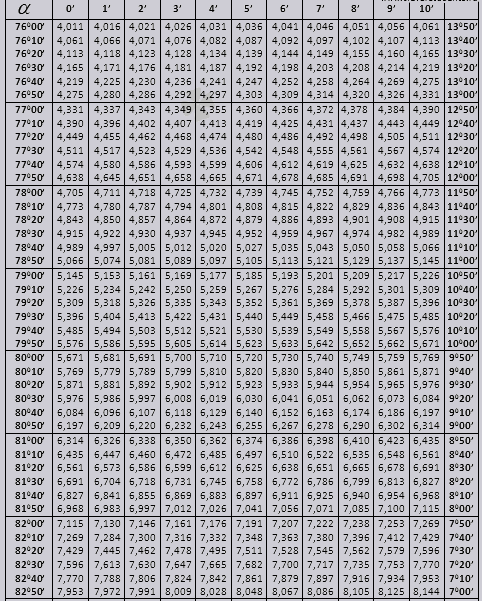

Асуудлыг шийдвэрлэхдээ Bradis хүснэгтийг хэрхэн ашиглахыг олж мэдье.
Гэм гэсэн тэмдэглэгээг олцгооё (зүүн ирмэгээс баганад байгаа тэмдэглэгээ) 42 минут (тэмдэглэгээ нь дээд мөрөнд байна). Гэмтсэнээр бид тэмдэглэгээг хайж байна, энэ нь = 0.3040 байна.
Минутын утгыг зургаан минутын интервалаар зааж өгсөн бөгөөд хэрэв бидэнд хэрэгтэй утга энэ интервалд багтаж байвал яах вэ. 44 минутыг авч үзье, хүснэгтэд ердөө 42 минут байна. Бид 42-ыг үндэс болгон авч, нэмэлт багануудыг ашиглана. баруун тал, бид 2-р нэмэлт өөрчлөлтийг авч 0.3040 + 0.0006 дээр нэмбэл 0.3046 болно.
Нүгэл 47 минутын хувьд бид 48 минутыг үндэс болгон авч, үүнээс 1 залруулга хасна, өөрөөр хэлбэл 0.3057 - 0.0003 = 0.3054.
Косыг тооцоолохдоо бид нүгэлтэй адил ажилладаг бөгөөд зөвхөн хүснэгтийн доод эгнээг үндэс болгон авдаг. Жишээ нь cos 20 0 = 0.9397
90 0 хүртэлх өнцгийн tg утгууд ба жижиг өнцгийн ор нь зөв бөгөөд тэдгээрт засвар байхгүй. Жишээлбэл, tg 78 0 37min = 4.967-г ол 
ба ctg 20 0 13 мин = 25.83 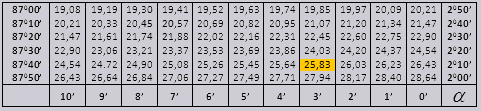
За, энд бид тригонометрийн үндсэн хүснэгтүүдийг авч үзсэн. Энэ мэдээлэл танд маш хэрэгтэй байсан гэж найдаж байна. Хүснэгт дээрх асуултууд, хэрэв байгаа бол сэтгэгдэл дээр бичихээ мартуузай!
Тайлбар: Ханын хаалт - ханыг хамгаалах самбар. Ханагүй хүрээгүй хаалт (http://www.spi-polymer.ru/otboyniki/) холбоосыг дагаж илүү ихийг олж мэдээрэй.
МЭӨ V зуунд эртний Грекийн гүн ухаантан Зенон Элеа өөрийн алдартай апориагаа томьёолсны дотор хамгийн алдартай нь "Ахиллес ба яст мэлхий" апориа юм. Энэ нь дараах байдалтай байна.Ахиллес яст мэлхийгээс арав дахин хурдан гүйж, түүнээс мянган алхмын ард байна гэж бодъё. Ахиллес энэ зайд гүйх үед яст мэлхий нэг чиглэлд зуун алхам мөлхдөг. Ахилл зуун алхам гүйхэд яст мэлхий дахиад арван алхам мөлхөх гэх мэт. Энэ үйл явц хязгааргүй үргэлжлэх бөгөөд Ахиллес яст мэлхийг хэзээ ч гүйцэхгүй.
Энэ үндэслэл нь дараагийн бүх үеийнхний хувьд логик цочрол болсон. Аристотель, Диоген, Кант, Гегель, Гилберт... Тэд бүгд нэг талаараа Зеногийн апориа гэж үзсэн. Цочрол маш хүчтэй байсан тул " ... өнөөгийн байдлаар хэлэлцүүлэг үргэлжилж, шинжлэх ухааны нийгэмлэг парадоксуудын мөн чанарын талаар нэгдсэн саналд хүрч чадаагүй байна ... математик шинжилгээ, олонлогийн онол, физик, философийн шинэ хандлага; Тэдний аль нь ч асуудлыг шийдэх нийтээр хүлээн зөвшөөрөгдсөн шийдэл болж чадаагүй ..."[Википедиа," Зеногийн Апориа "]. Хүн бүр өөрсдийгөө хуурч байгааг ойлгодог, гэхдээ хэн ч хууран мэхлэлт гэж юу болохыг ойлгодоггүй.
Математикийн үүднээс авч үзвэл Зено өөрийн апориадаа үнэ цэнээс шилжихийг тодорхой харуулсан. Энэ шилжилт нь тогтмолуудын оронд хэрэглэхийг хэлнэ. Миний ойлгож байгаагаар хувьсах хэмжлийн нэгжийг хэрэглэх математикийн аппарат хараахан болоогүй, эсвэл Зеногийн апорид хэрэглээгүй байна. Бидний ердийн логикийг ашиглах нь биднийг урхинд оруулдаг. Бид сэтгэлгээний инерцийн тусламжтайгаар цаг хугацааны тогтмол нэгжийг харилцан адилтгахад ашигладаг. Ахиллес яст мэлхийг гүйцэж түрүүлэх тэр мөчид цаг хугацаа бүрмөсөн зогсч, бие махбодийн үүднээс авч үзвэл цаг хугацаа удааширч байгаа мэт харагдана. Хэрэв цаг хугацаа зогсвол Ахиллес яст мэлхийг гүйцэж түрүүлж чадахгүй.
Хэрэв бид дассан логикоо эргүүлбэл бүх зүйл байрандаа орно. Ахиллес тогтмол хурдтайгаар гүйдэг. Замынхаа дараагийн хэсэг бүр өмнөхөөсөө арав дахин богино байна. Үүний дагуу үүнийг даван туулахад зарцуулсан хугацаа өмнөхөөсөө арав дахин бага байна. Хэрэв бид энэ нөхцөлд "хязгааргүй" гэсэн ойлголтыг хэрэглэвэл "Ахиллес яст мэлхийг хязгааргүй хурдан гүйцэх болно" гэж хэлэх нь зөв байх болно.
Энэ логик урхинаас хэрхэн зайлсхийх вэ? Тогтмол цаг хугацааны нэгжид үлдэж, харилцан хамааралтай утга руу бүү шилжинэ. Зеногийн хэлээр энэ нь дараах байдалтай байна.
Ахиллес мянган алхам гүйхэд яст мэлхий нэг зүгт зуун алхам мөлхдөг. Дараагийн цагийн интервалд эхнийхтэйгээ тэнцэх хугацаанд Ахиллес дахиад мянган алхам гүйж, яст мэлхий зуун алхам мөлхөх болно. Одоо Ахиллес яст мэлхийнээс найман зуун алхмын урд байна.
Энэ хандлага нь бодит байдлыг ямар ч логик парадоксгүйгээр хангалттай дүрсэлдэг. Гэхдээ тийм биш бүрэн шийдэлАсуудлууд. Эйнштейний гэрлийн хурдыг давж гаршгүй тухай хэлсэн үг нь Зеногийн "Ахиллес ба яст мэлхий" апориатай тун төстэй юм. Энэ асуудлыг судалж, дахин бодож, шийдэж чадаагүй л байна. Мөн шийдлийг хязгааргүй олон тоогоор бус хэмжилтийн нэгжээр хайх ёстой.
Зеногийн өөр нэг сонирхолтой апориа нь нисдэг сумны тухай өгүүлдэг:
Нисдэг сум нь цаг мөч бүрт амарч, цаг мөч бүрт амарч байдаг тул үргэлж тайван байдаг тул хөдөлгөөнгүй байдаг.
Энэ апорид логик парадоксыг маш энгийнээр даван туулдаг - цаг мөч бүрт нисдэг сум сансар огторгуйн өөр өөр цэгүүдэд байрладаг гэдгийг тодруулахад хангалттай бөгөөд энэ нь хөдөлгөөн юм. Энд бас нэг анхаарах зүйл бий. Зам дээрх машины нэг гэрэл зургаас түүний хөдөлгөөний баримт, түүнд хүрэх зайг тодорхойлох боломжгүй юм. Машины хөдөлгөөний баримтыг тодорхойлохын тулд нэг цэгээс өөр өөр цаг үед авсан хоёр гэрэл зураг шаардлагатай боловч зайг тодорхойлоход ашиглах боломжгүй юм. Машин хүртэлх зайг тодорхойлохын тулд сансар огторгуйн өөр өөр цэгээс нэгэн зэрэг авсан хоёр гэрэл зураг хэрэгтэй боловч тэдгээрийн хөдөлгөөний баримтыг тодорхойлох боломжгүй (байгалийн хэрэг танд тооцоололд нэмэлт мэдээлэл хэрэгтэй хэвээр байна, тригонометр танд туслах болно). Би юунд анхаарлаа хандуулмаар байна Онцгой анхаарал, цаг хугацааны хоёр цэг, сансар огторгуйн хоёр цэг нь өөр өөр зүйл бөгөөд андуурч болохгүй, учир нь тэдгээр нь хайгуул хийх өөр өөр боломжийг олгодог.
2018 оны 7-р сарын 4, Лхагва гараг
Багц ба олон багцын ялгааг Википедиад маш сайн тайлбарласан болно. Бид харж байна.
Таны харж байгаагаар "иж бүрдэл нь хоёр ижил элементтэй байж болохгүй", гэхдээ олонлогт ижил элементүүд байгаа бол ийм олонлогийг "олон багц" гэж нэрлэдэг. Ухаантай хүмүүс ийм утгагүй логикийг хэзээ ч ойлгохгүй. Энэ бол ярьдаг тоть, сургасан сармагчингийн түвшин бөгөөд оюун ухаан нь "бүрэн" гэсэн үгнээс ангид байдаг. Математикчид энгийн сургагч багшийн үүрэг гүйцэтгэж, өөрсдийн утгагүй санаагаа бидэнд номлодог.
Нэгэн удаа гүүрийг барьсан инженерүүд гүүрний туршилтын үеэр гүүрэн доорх завинд сууж байсан. Хэрэв гүүр нурсан бол дунд зэргийн инженер өөрийн бүтээлийн нуранги дор нас баржээ. Гүүр ачааллыг даах чадвартай бол авъяаслаг инженер өөр гүүрүүдийг барьсан.
Математикчид "намайг бод, би гэрт байна" гэсэн хэллэгийн ард хэчнээн нуугдаж байгаагаас үл хамааран "математик хийсвэр ойлголтыг судалдаг" гэсэн хэллэгийг бодит байдалтай салшгүй холбодог нэг хүйн зангилаа байдаг. Энэ хүйн бол мөнгө. Хэрэглэх боломжтой математикийн онолматематикчдад өөрсдөд нь тавьдаг.
Математикийн хичээлийг маш сайн сурсан, одоо цалингаа өгөөд кассанд сууж байна. Энд нэг математикч мөнгөө авахаар манайд ирдэг. Бид түүнд бүх дүнг тоолж, ширээн дээр өөр өөр овоолго болгон тавьж, ижил мөнгөн дэвсгэртийг тавьдаг. Дараа нь бид овоо бүрээс нэг дэвсгэрт авч, математикчдаа "математикийн цалингийн багц"-ыг өгнө. Ижил элементгүй олонлог нь ижил элементтэй олонлогтой тэнцүү биш гэдгийг нотлох үед л тэр үлдсэн үнэт цаасыг хүлээн авна гэж бид математикийг тайлбарладаг. Эндээс л зугаа цэнгэл эхэлдэг.
Юуны өмнө, депутатуудын логик ажиллах болно: "Та үүнийг бусдад хэрэглэж болно, гэхдээ надад биш!" Цаашилбал, ижил мөнгөн дэвсгэрт дээр өөр өөр мөнгөн дэвсгэрт байгаа гэсэн баталгааг гаргаж эхлэх бөгөөд энэ нь тэдгээрийг ижил элемент гэж үзэх боломжгүй гэсэн үг юм. За, бид цалингаа зоосоор тооцдог - зоосон дээр ямар ч тоо байхгүй. Энд математикч физикийг сануулах болно: өөр өөр зооснууд өөр өөр хэмжээтэй шороотой байдаг, зоос бүрийн атомын талст бүтэц, зохион байгуулалт нь өвөрмөц юм ...
Одоо надад хамгийн их байна сонирхол Асуу: олонлогийн элементүүд олонлогийн элементүүд болон эсрэгээр хувирах зааг хаана байх вэ? Ийм шугам байдаггүй - бүх зүйлийг бөө нар шийддэг, энд шинжлэх ухаан ч ойрхон байдаггүй.
Энд харах. Бид ижил талбай бүхий хөлбөмбөгийн цэнгэлдэхүүдийг сонгодог. Талбайн талбай нь ижил бөгөөд энэ нь бид олон багцтай гэсэн үг юм. Гэхдээ ижил цэнгэлдэхүүдийн нэрийг авч үзвэл нэр нь өөр учраас маш их зүйлийг олж авдаг. Таны харж байгаагаар ижил элементүүдийн багц нь нэгэн зэрэг олонлог ба олон багц юм. Хэр зөв бэ? Тэгээд энд математикч-бөө-Шуллер ханцуйнаасаа бүрээ гарган бидэнд багц эсвэл олон багцын тухай ярьж эхлэв. Ямар ч байсан тэр бидний зөв гэдэгт итгүүлэх болно.
Орчин үеийн бөө нар олонлогийн онолыг бодит байдалтай уялдуулан хэрхэн ажилладагийг ойлгохын тулд нэг олонлогийн элементүүд нөгөө олонлогийн элементүүдээс юугаараа ялгаатай вэ гэсэн нэг асуултад хариулахад хангалттай. Би та нарт ямар ч "нэг бүхэл бүтэн биш" эсвэл "нэг бүхэл бүтэн байдлаар төсөөлөгдөхгүй" гэдгийг харуулах болно.
2018 оны 3-р сарын 18, Ням гараг
Тооны цифрүүдийн нийлбэр гэдэг нь математикт огт хамааралгүй бөөгийн хэнгэрэгтэй бүжиг юм. Тийм ээ, математикийн хичээл дээр бид тооны цифрүүдийн нийлбэрийг олоод хэрэглэхийг заадаг ч тэрний төлөө бөө нар, үр хойчдоо эрдэм ухаан, мэргэн ухааныг нь зааж сургана, тэгэхгүй бол бөө нар зүгээр л үхнэ.
Танд нотлох баримт хэрэгтэй байна уу? Wikipedia-г нээгээд "Тооны цифрүүдийн нийлбэр" хуудсыг олохыг хичээ. Тэр байхгүй. Аливаа тооны цифрүүдийн нийлбэрийг олох томьёо математикт байдаггүй. Эцсийн эцэст тоо бол бидний тоо бичдэг график тэмдэг бөгөөд математикийн хэлээр даалгавар нь иймэрхүү сонсогддог: "Аливаа тоог илэрхийлэх график тэмдгийн нийлбэрийг ол." Математикчид энэ асуудлыг шийдэж чадахгүй, харин бөө нар үүнийг энгийн байдлаар шийдэж чадна.
Өгөгдсөн тооны цифрүүдийн нийлбэрийг олохын тулд юу хийж, яаж хийхийг олж мэдье. Тэгэхээр 12345 тоо байна гэж бодъё. Энэ тооны цифрүүдийн нийлбэрийг олохын тулд юу хийх хэрэгтэй вэ? Бүх алхамуудыг дарааллаар нь авч үзье.
1. Цаасан дээр тоог бич. Бид юу хийсэн бэ? Бид дугаарыг тоон график тэмдэг болгон хөрвүүлсэн. Энэ бол математикийн үйлдэл биш юм.
2. Бид хүлээн авсан нэг зургийг тусдаа тоо агуулсан хэд хэдэн зураг болгон хуваасан. Зургийг тайрах нь математикийн үйлдэл биш юм.
3. График тэмдэгтүүдийг тоо болгон хувиргах. Энэ бол математикийн үйлдэл биш юм.
4. Гарсан тоонуудыг нэм. Одоо энэ бол математик.
12345 тооны цифрүүдийн нийлбэр нь 15. Математикчдын хэрэглэдэг бөө нарын "зүсэх, оёх курс" юм. Гэхдээ энэ нь бүгд биш юм.
Математикийн үүднээс авч үзвэл бид аль тооны системд тоог бичих нь хамаагүй. Тэгэхээр, in өөр өөр системүүдТооцооллын дагуу ижил тооны цифрүүдийн нийлбэр өөр байх болно. Математикийн хувьд тооны системийг тоон баруун талд байрлах доод үсэг болгон заадаг. Олон тооны 12345 байгаа тул би толгойгоо хуурахыг хүсэхгүй байна, тухай нийтлэлээс 26 дугаарыг анхаарч үзээрэй. Энэ тоог хоёртын, наймтын, аравтын, арван зургаатын тооллын системд бичье. Бид алхам бүрийг микроскопоор авч үзэхгүй, бид үүнийг аль хэдийн хийсэн. Үр дүнг харцгаая.
Таны харж байгаагаар өөр өөр тооны системд ижил тооны цифрүүдийн нийлбэр өөр өөр байдаг. Энэ үр дүн нь математиктай ямар ч холбоогүй юм. Тэгш өнцөгтийн талбайг метр, сантиметрээр олох нь огт өөр үр дүн өгөхтэй адил юм.
Бүх тооллын системд тэг нь адилхан харагддаг бөгөөд цифрүүдийн нийлбэр байдаггүй. Үүнийг дэмжсэн өөр нэг үндэслэл нь . Математикчдад зориулсан асуулт: тоо биш гэдгийг математикт хэрхэн тэмдэглэдэг вэ? Математикчдын хувьд тооноос өөр юу ч байхгүй гэж юу вэ? Бөөгийн хувьд үүнийг зөвшөөрч болох ч эрдэмтдийн хувьд бол үгүй. Бодит байдал зөвхөн тоон дээр тогтдоггүй.
Хүлээн авсан үр дүнг тоон систем нь тоон хэмжилтийн нэгж гэдгийг нотлох баримт гэж үзэх ёстой. Эцсийн эцэст бид өөр өөр хэмжүүр бүхий тоонуудыг харьцуулж болохгүй. Хэрэв ижил хэмжигдэхүүнийг өөр өөр хэмжих нэгжүүдтэй ижил үйлдэл хийхэд хүргэдэг өөр өөр үр дүнТэднийг харьцуулсны дараа математиктай ямар ч холбоогүй болно.
Жинхэнэ математик гэж юу вэ? Энэ бол үр дүн юм математик үйлдэлтоон утга, ашигласан хэмжих нэгж, энэ үйлдлийг хэн гүйцэтгэхээс хамаарахгүй.
Өө! Энэ эмэгтэйчүүдийн бие засах газар биш гэж үү?
- Залуу эмэгтэй! Энэ бол тэнгэрт өргөгдсөн сүнснүүдийн хязгааргүй ариун байдлыг судлах лаборатори юм! Дээрээс нь Nimbus, дээшээ сум. Өөр ямар бие засах газар вэ?
Эмэгтэй... Дээд талын гэрэлт цагираг, доош сум нь эрэгтэй.
Хэрэв таны нүдний өмнө өдөрт хэд хэдэн удаа дизайны урлагийн бүтээл анивчдаг бол
Дараа нь та машиндаа гэнэт хачирхалтай дүрс олж авахад гайхах зүйл алга.
Би хувьдаа баас хийж буй хүнд хасах дөрвөн градусыг (нэг зураг) харахыг хичээдэг (хэд хэдэн зургийн найрлага: хасах тэмдэг, дөрөв, градусын тэмдэглэгээ). Би энэ охиныг физик мэдэхгүй тэнэг гэж үзэхгүй байна. Тэр зүгээр л график дүрсийг хүлээн авах хэвшмэл ойлголттой байдаг. Үүнийг математикчид бидэнд байнга заадаг. Энд нэг жишээ байна.
1А нь "хасах дөрвөн градус" эсвэл "нэг а" биш юм. Энэ бол арван зургаатын тооллын систем дэх "баасан хүн" буюу "хорин зургаа" гэсэн тоо юм. Энэ тооны системд байнга ажилладаг хүмүүс тоо, үсгийг нэг график тэмдэг болгон автоматаар хүлээн авдаг.







