Різнинне рівняння приклад. Вирішення звичайних лінійних різницевих рівнянь із постійними коефіцієнтами. Диференціальні рівняння систем автоматичного регулювання. Методика складання диференціальних рівнянь систем автоматичного регулювання

Застосування рівнянь поширене у нашому житті. Вони використовуються в багатьох розрахунках, будівництві споруд та навіть спорті. Рівняння людина використовувала ще в давнину і відтоді їх застосування лише зростає. Різнісне рівняння є рівнянням, що зв'язує значення деякої невідомої функції в будь-якій точці з її значенням в одній або декількох точках, віддалених від даної на певний інтервал. Приклад:

\[Г(z+1) = zГ(z)\]

Для різницевих рівняньз постійними коефіцієнтамиіснують детально розроблені методи знаходження рішення у замкнутій формі. Неоднорідне і однорідне різницеві рівняння n-го порядку задаються відповідно до рівнянь, де \ постійні коефіцієнти.

Однорідні різницеві рівняння.

Розглянемо рівняння n-го порядку

\[(a_nE^n +a(n-1)E^n1 + \cdots +a_1Е + a_1)y(k) = 0 \]

Пропоноване рішення слід шукати у вигляді:

де \ - Постійна величина, що підлягає визначенню. Вигляд передбачуваного рішення, що задається рівнянням, не є найпоширенішим. Допустимі значення\ служать корінням многочлена від \[ е^r.\] При \[ \beta = е^r \]передбачуване рішення стає таким:

де [beta] - підлягає визначенню постійна величина. Підставляючи рівняння та враховуючи \, отримаємо наступне характеристичне рівняння:

Неоднорідні різницеві рівняння. Метод невизначених коефіцієнтів. Розглянемо різницеве ​​рівняння n-го порядку

\[(a_nЕn +а_(n-1)Еn^-1+\cdots+ а_1Е +a_1)y(k) =F(k) \]

Відповідь має наступний вигляд:

Де можна вирішити різницеве ​​рівняння онлайн?

Вирішити рівняння можна на нашому сайті https://сайт. Безкоштовний онлайн вирішувач дозволить вирішити рівняння онлайн будь-якої складності за лічені секунди. Все, що вам необхідно зробити – це просто ввести свої дані у вирішувачі. Також ви можете переглянути відео інструкцію та дізнатися, як вирішити рівняння на нашому сайті. А якщо у вас залишилися питання, ви можете задати їх у нашій групі Вконтакте http://vk.com/pocketteacher. Вступайте до нашої групи, ми завжди раді допомогти вам.

На практиці найпростіші різницеві рівняння виникають при дослідженні, наприклад, величини банківського вкладу. Ця величина є змінною Y x , що становить суму, що накопичується за встановленим законом при цілих значеннях аргументу x. Нехай сума Y o покладена до банку за умови нарахування 100 r складних відсотків на рік. Нехай нарахування відсотків проводиться один раз на рік та xпозначає кількість років із моменту приміщення вкладу (x = 0, 1, 2,...). Позначимо величину вкладу після закінчення xроків через Y x. Ми отримуємо

Y x= (1+r)Y x-1.

Якщо початкова сума становить Y o ми приходимо до завдання відшукання рішення отриманого різницевого рівняння, підпорядкованого початковій умові Y x = Y o при x = 0. Отримане різницеве ​​рівняння містить Y x і значення цієї змінної на один рік раніше, тобто. Y x-1; в даному випадкуаргумент xявно не входить у різницеве ​​рівняння.

Взагалі кажучи, звичайне різницеве ​​рівняннявстановлює зв'язок між значеннями функції Y = Y(x ), що розглядається для ряду рівновіддалених значень аргументу x, Але можна без обмеження спільності вважати, що потрібна функція визначена для рівновіддалених значень аргументу з кроком, рівним одиниці. Таким чином, якщо початкове значення аргументу є x, то ряд його рівновіддалених значень буде x , x+1, x+2,... і у зворотному напрямку: x , x-1, x-2,.... Відповідні значення функції позначатимемо Y x, Y x+ 1, Y x+2, ... або Y x , Y x-1, Y x-2, .... Визначимо так звані різницірізних порядків функції Y x за допомогою наступних формул:

Різниці першого порядку

D Y x = Y x +1 - Y x ,

D Y x+1 = Y x+2 - Y x+1,

D Y x +2 = Y x +3 - Y x +2,

... ... ... ... ...

Різниці другого порядку

D 2 Y x = D Y x +1 - D Y x ,

D 2 Y x+1 = D Y x+2 - D Y x+1 ,

D 2 Y x+2 = D Y x+3 - D Y x+2 ,

... ... ... ... ...

Різниці третього порядку

D 3 Y x = D 2 Y x +1 - D 2 Y x ,

D 3 Y x+1 = D 2 Y x+2 - D 2 Y x+1 ,

... ... ... ... ...

Звичайним різницевим рівнянням називається рівняння, що зв'язує значення одного незалежного аргументу x, його функції Y xта різниць різних порядків цієї функції D Y x, D 2 Y x, D 3 Y x, .... Таке рівняння можна записати в загальному виглядінаступним чином:

j ( x , Y x , D Y x, D 2 Y x D 3 Y x , D n Y x ) = 0, (10.1)

якеформою аналогічно диференціальному рівнянню.

Порядкомрізницевого рівняння називається порядок найвищої різниці, що входить до цього рівняння. Різнинне рівняння (10.1) часто зручніше записати, користуючись не різницею невідомої функції, а її значеннями при послідовних значеннях аргументу, тобто виразити D Y x, D 2 Y x, D 3 Y x ,... через Y x , Y x+1 , Y x+2, .... Рівняння (10.1) можна привести до однієї з двох форм:

y ( x , Y x , Y x+1, ...,Y x+n ) = 0, (10.2)

x ( x, Y x, Y x-1, ..., Y x -n) = 0.(10.3)

Загальне дискретне рішення Y x звичайного різницевого рівняння n-го порядку представляє функцію x (x = 0, 1. 2, ...), що містить рівно nдовільних постійних:

Y x= Y(x, C 1 , C 2 ,..., C n).

Павутиноподібна модель

Нехай ринок якогось окремого товару характеризується наступними функціямипопиту та пропозиції:

D = D(P), S = S(P).

Для існування рівноваги ціна має бути такою, щоб товар на ринку був розпроданий, або

D( P) = S(P).

Ціна рівноваги задається цим рівнянням (яке може мати безліч рішень), а відповідний обсяг купівель-продажів, що позначається через, - Наступним рівнянням:

D() = S().

Динамічна модельвиходить за наявності запізнення попиту чи пропозиції. Найпростіша модельв дискретному аналізівключає постійне запізнення або відставання пропозиції на один інтервал:

D t= D (P t) та S t = S (P t-1).

Це може статися, якщо для товару, що розглядається, потрібно певний період часу, обраний за інтервал. Дія моделі така: при заданому P t-1 попереднього періоду обсяг пропозиції на ринку в поточному періоді буде S (P t-1), і величина P t повинна встановити так, щоб був куплений весь обсяг запропонованого товару. Іншими словами, P t та обсяг купівель-продажів X t характеризуються рівнянням:

X t= D(Pt) = S(Pt-1).

Отже, знаючи вихідну ціну P o за допомогою цих рівнянь ми можемо отримати значення P 1 і X 1. Потім, використовуючи наявну ціну P 1, з відповідних рівнянь отримаємо значення P 2 і X 2 і т.д. Загалом зміна P t характеризується різницевим рівнянням першого порядку ( одноінтервальневідставання):

D(Pt) = S(Pt-1).

Рішення можна проілюструвати діаграмою, представленою на рис.5, де D і S - відповідно криві попиту та пропозиції, а положення рівноваги (зі значеннямиі ) відповідає точці їх перетину Q. Ціна в початковий момент часу дорівнює P o . Відповідна точка Q o на кривій S дає обсяг пропозиції в період 1. Весь цей запропонований обсяг товару розкуповується за ціною P 1 , заданою точкою Q 1 на кривій D з тією ж ординатою (X 1), що і Q o . У другий період руху відбувається спочатку по вертикалі від точки Q 1 до точки на кривій S, що дає X 2, а потім по горизонталі - до точки Q 2 на кривій D. Остання точка характеризує P 2 . Продовження цього процесу дає графік павутинняпоказаний на рис. 5. Ціни та обсяги (купівель - продажів) у послідовні періоди часу є відповідно координатами точок Q 1 , Q 2 , Q 3 ,... на кривій попиту D. У даному випадку послідовність точок прагне до Q. При цьому точки по черзі розташовуються на лівий і правій сторонівід Q. Отже, значення ціни P t прагнуть до, по черзі по обидва боки від. Так само і з обсягами купівель - продажів (X t ).

Рішення можна отримати алгебраїчно для випадку лінійних функційпопиту та пропозиції: D = a + aP, S = b + bP. Значення рівновагиі будуть задані рівняннями

A + a = b + b ,

тобто

= (a - b) / (b - a), = (b a - a b) / (b - a). (10.4). р t-1.

(10.7) Рівняння (10.7) аналогічні (10.5), крім того, що вони описують відхилення від рівнів рівноваги (тепер відомо, що є). Обидва ці рівняння є різницевими рівняннями першого порядку. Покладемо c = b /a і підставимо його до рівняння (10.7), так що різницеве ​​рівняння щодо р t

буде р = t

c р t-1. (10.8) будеПри даному значенні

буде o в момент t = 0 з (10.8) отримуємо рішення: буде t =

o c t,

або

P t = + (P o -) c t.

Вирішення звичайних лінійних різницевих рівнянь

з постійними коефіцієнтами

,

Зв'язок виходу та входу лінійної дискретної системи може бути описаний звичайним лінійним різницевим рівнянням з постійними коефіцієнтами деy[ n] n,

- Вихідний сигнал в моментy[ x[ n,

- вхідний сигнал у моментa i , b k

- Постійні коефіцієнти.

• Для вирішення таких рівнянь можуть використовуватись два методи
• Прямий метод,

Метод Z – перетворення.

Спочатку розглянемо рішення лінійного різницевого рівняння за допомогою прямого методу. Загальне рішення неоднорідного (з відмінною від нуляправою частиною ) лінійного різницевого рівняння дорівнює сумі провищого рішення лінійного однорідного різницевого рівняння таприватного рішення не

однорідного рівняння Загальне рішення однорідного різницевого рівняння (zero-input) responsey[

y h [

.

визначається у вигляді

Підставляючи це рішення в однорідне рівняння, отримуємо Такий поліном називаютьхарактеристичний поліном системи. Він має N . Коріння може бути дійсним або комплексним і деякі коріння - збігаються (кратними).

Якщо коріння є дійсними та різними, то рішення однорідного рівняння має вигляд

де коефіцієнти

Якщо деякий корінь, наприклад, λ 1має кратність m, то відповідний йому член рішення набуває форми

Якщо всі коефіцієнти однорідного рівняння і відповідно характеристичного багаточлена дійсні, то два члени рішення, що відповідають простим комплексно пов'язаним корінням можна уявити (записати) у вигляді , при цьому коефіцієнти A,Bвизначаються за початковими умовами.

Вигляд приватного рішення y p [y[рівняння залежить від правої частини (вхідного сигналу) і визначається згідно з наведеною нижче таблицею

Таблиця 1. Вид приватного рішення для різного характеру правої частини

Вхідний сигналx[n]	Приватне рішенняy p [n]
A(Константа)

Рішення лінійного різницевого рівняння методом Z – перетворення полягає у застосуванні Z- Перетворення до рівняння з використанням властивостей лінійності та тимчасового зсуву. В результаті виходить лінійне алгебраїчне рівняннящодо Z- Зображення шуканої функції. Назад Z- Перетворення дає шукане рішення в тимчасовій області. Для отримання зворотного Z - перетворення найчастіше використовується розкладання раціонального виразу на прості (елементарні) дроби, оскільки зворотне перетворення від окремого елементарного дробу має простий вигляд.

Зауважимо, що з переходу у тимчасову область можуть використовуватися інші методи обчислення зворотного Z – перетворення.

приклад. Визначимо відгук (вихідний сигнал) системи, що описується лінійним різницевим рівнянням на вхідний сигнал

Рішення.

1. Прямий метод розв'язання рівняння.

Однорідне рівняння. Його характеристичний поліном.

Коріння полінома .

Рішення однорідного рівняння.

Оскільки то приватне рішення визначаємо у вигляді .

Підставляємо його в рівняння

Для знаходження константи Доприймемо n = 2. Тоді

Або , К = 2,33

Звідси приватне рішення і загальне рішеннярізницевого рівняння (1)

Знайдемо константи З 1і З 2. Для цього покладемо n = 0тоді з вихідного різницевого рівняння отримуємо. Для цього рівняння

Тому. З виразу (1)

Отже,

.

З виразу (1) для n = 1маємо.
Отримуємо наступні два рівняння для 1 і 2

.

Рішення цієї системи дає такі значення: 1 =0,486 і 2 = -0,816.

Отже, загальне рішення даного рівняння

2. Рішення шляхом Z – перетворення.

Візьмемо Z – перетворення від вихідного різницевого рівняння, враховуючи властивість (теорему) тимчасового зсуву 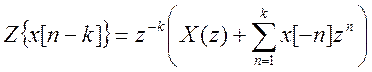. Отримуємо

Контрольні питання:

1. Яка функція називається сітковою?

2. Яке рівняння називається різницевим?

3. Які рівняння називаються різницевими рівняннями 1-го порядку?

4. Як виявляється загальне рішення неоднорідного різницевого рівняння 1-го порядку?

5. Яке рішення різницевого рівняння називається фундаментальним?

6. Чому загальне рішення однорідного рівняння з постійними коефіцієнтами має вигляд геометричній прогресії?

Завдання.

1. Написати процедуру вирішення різницевого рівняння першого порядку з початковою умовою.

2. Для заданого рівняннязнайти загальне та приватне рішення аналітично.

3. Порівняти результати обчислень за рекурентною формулою з аналітичним рішенням.

4. З'ясувати, як впливає результат обурення початкової умови, коефіцієнтів рівняння, правої частини.

				Вказівки

Знайдемо загальне рішення різницевого рівняння 1-го порядку

. (1)

Приватне рішення однорідного рівняння при отримаємо, використовуючи рекурентну формулу: . Оскільки значення Y у кожному наступному вузлі сітки подвоюється, виходить геометрична прогресія із знаменником q=2:

Приватне рішення неоднорідного рівняннязнайдемо у вигляді: , де А – невизначений коефіцієнт. Тоді , , і прирівнявши отримане значення до заданої правої частини, знайдемо невизначений коефіцієнт A =. Остаточно, загальне рішення: .

Використовуючи початкову умову, знаходимо константу: . Остаточно, приватне рішення за заданою початковою умовою:

.

Для дослідження стійкості рішення до обурення самого рішення та початкової умови розглянемо таке рівняння:

з обуреною початковою умовою

(Тут - величина обурення). Віднімаючи вихідне рівняння (1), отримаємо різницеве ​​рівняння для обурення:

з початковою умовою. Вирішення цього рівняння має вигляд: , тобто. навіть мале обурення у якомусь вузлі експоненційно зростає зі збільшенням номера вузла.

Студенту необхідно проілюструвати сказане вище: дослідити вплив збурень початкової умови, правих частин та коефіцієнтів рівняння, змінивши рекурентну формулу.

Варіант, відповідно до номера студента за списком у журналі, необхідно вирішити мовою програмування C++ (допускається використання середовища Builder) або Pascal (допускається використання середовища Delphi).

1. Рекурентна формула для одержання чисельного рішення.
2. Аналітичне рішення різницевого рівняння.
3. Загальне рішення та приватне рішення, що задовольняє заданим початковим умовам.

Дослідити стійкість рішення до обурення початкової умови та рішення аналітично.

б) при збуренні коефіцієнтів рівняння;

в) під час обурення правої частини.

Контрольні питання:

Тема:Розносні рівняння 2 порядку

1. Які рівняння називаються різницевими рівняннями 2-го порядку?

2. Що таке характеристичне рівняння?

3. Як виглядає приватне рішення однорідного різницевого рівняння 2-го порядку з дійсним корінням характеристичного рівняння?

4. Як виглядає приватне рішення однорідного різницевого рівняння 2-го порядку з комплексним корінням характеристичного рівняння?

5. Як перебуває загальне рішення неоднорідного різницевого рівняння 2-го порядку?

6. Що таке чисельне та аналітичне рішення різницевого рівняння 2-го порядку?

7. Які завдання називаються добре обумовленими?

Завдання

1. Написати процедуру вирішення різницевої крайової задачі для рівняння другого порядку з граничними умовами;

2. Для заданого рівняння знайти загальне та приватне рішення аналітично та перевірити критерій обумовленості.

3. Порівняти результати обчислень за рекурентною формулою з аналітичним рішенням.

						4. З'ясувати, як впливає на результат обурення граничних умов та правої частини. Знайдемо загальне рішення різницевого рівняння 2-го порядку можна знайти вибором довільних постійних. (Поряд із завданнями Коші, для рівнянь 2-го порядку розглядаються також двоточкові крайові завдання, в яких задані значення сіткової функції у двох вузлах, розташованих не підряд, а на кінцях деякого кінцевого відрізка: граничні умови ). Аналітичне розв'язання такого завдання можна отримати відповідним вибором довільних постійних у загальному рішенні. Однак, на відміну від завдання з початковими умовами, крайове завдання не обов'язково буде однозначно вирішуваним. Томувелике значення має з'ясування класу крайових завдань, які мають однозначну розв'язність і слабку чутливість до обурення (внаслідок помилок округлення) правих частин і граничних умов. Такі завдання називатимемо добре обумовленими Розглянемо приклад погано обумовленого крайового завдання Постановка задачі. Вихідне різницеве ​​рівняння та граничні умови. Процедура отримання чисельного рішення. Графіки чисельного рішення та аналітичного рішення (в одних осях). Графік різниці чисельного та аналітичного рішення. Графіки обурених чисельних рішеньта різниці обуреного та необуреного рішень: а) під час обурення початкової умови; б) під час обурення правої частини. Висновок про обумовленість крайового завдання.

Рівняння виду

де деякі числа називається лінійним різницевим рівнянням з постійними коефіцієнтами.

Зазвичай замість рівняння (1) розглядається рівняння, яке виходить із (1) шляхом переходу від кінцевих різниць до значення функції, тобто рівняння виду

Якщо у рівнянні (2) функція, таке рівняння називається однорідним.

Розглянемо однорідне рівняння

Теорія лінійних різницевих рівнянь аналогічна до теорії лінійних диференціальних рівнянь.

Теорема 1.

Якщо функції є рішення однорідного рівняння (3), то функція

також є розв'язком рівняння (3).

Доведення.

Підставимо функції (3)

функція є рішенням рівняння (3).

Гратчасті функції називаються лінійно залежними, якщо знайдуться такі числа, причому хоча б одне від нуля, для будь-якого n справедливо:

(4)

Якщо (4) має місце тільки за то функції називаються лінійно незалежними.

Будь-яке k лінійно незалежних рішень рівняння (3) утворюють фундаментальну системурішень.

Нехай лінійно незалежні рішення рівняння (3), тоді

є загальним рішенням рівняння (3). При знаходженні конкретної умови визначається з початкових умов

Шукатимемо рішення рівняння (3) у вигляді:

Підставимо в рівняння (3)

Поділимо рівняння (5) на

Характеристичне рівняння. (6)

Припустимо, що (6) має тільки просте коріння Неважко переконатися, що є лінійно незалежними. Загальне рішення однорідного рівняння (3) має вигляд

приклад.

Розглянемо рівняння

Характеристичне рівняння має вигляд

Рішення має вигляд

Нехай корінь має кратність r. Цьому кореню відповідає рішення

Якщо припустити, що решта коріння не є кратними, то загальне рішення рівняння (3) має вигляд

Розглянемо загальне рішення неоднорідного рівняння (2).

Приватне рішення неоднорідного рівняння (2), тоді загальне рішення

лекція 16

План лекції

1. Поняття про D та Z - перетворення.

2. Область застосування D та Z - перетворень.

3. Зворотні D та Z - перетворення.

ДИСКРЕТНЕ ПЕРЕТВОРЕННЯ ЛАПЛАСУ.

Z – ПЕРЕТВОРЕННЯ.

У прикладних дослідженнях, пов'язаних з використанням ґратчастих функцій, широко застосовується дискретне перетворенняЛапласа (Д – перетворення) та Z – перетворення. За аналогією зі звичайним перетворенням Лапласа дискретне задається у вигляді

де (1)

Символічно Д – перетворення записується як

Для зміщених ґратчастих функцій

де – зміщення.

Z - перетворення виходить з Д - перетворення підстановкою і задається співвідношенням

(3)

Для зміщеної функції

Функція називається оригіналом, якщо

2) існує показник зростання, тобто знайдуться такі і що

(4)

Найменше з чисел (або межа, до якої прагне найменше число), для якого справедлива нерівність (4), називається абсцисою абсолютної збіжності і позначається

Теорема.

Якщо функція є оригіналом, зображення визначено в області Re p > і є в цій області аналітичною функцією.

Покажемо, що з Re p > ряд (1) абсолютно сходиться. Маємо

т. до. зазначена сума є сумою членів спадної геометричної прогресії з показником Відомо, що така прогресія сходиться. Величину можна взяти як завгодно близькій величині, тобто перша частина теореми доведена.

Другу частину теореми приймемо без доказів.

Зображення є періодичною функцієюз уявним періодом

При вивченні зображення немає сенсу розглядати його на всій комплексній площині, достатньо обмежитися вивченням у будь-якій смузі шириною. яка називається основною. Т. о. Можна вважати, що зображення визначено у підлозі смузі

і є у цій підлозі смузі аналітичною функцією.

Знайдемо область визначення та аналітичності функції F(z), поклавши . Покажемо, що напівсмуга площині p перетворенням перетворюється на область на площині z: .

Справді, відрізок , що обмежує підлозі смугу на площині p, переводиться на площині z в околицю: .

Позначимо через лінію, на яку перетворення переводить відрізок . Тоді

Околиця.

Т. о. Z – перетворення F(z) визначено області і є у цій галузі аналітичної функцією.

Зворотне Д – перетворення дозволяє за зображенням відновити гратчасту функцію

(5)

Доведемо справедливість рівності.

Лежать усередині околиці.

(7)

(8)

У рівностях (7) і (8) відрахування беруться за всіма особливим точкамфункції F(s).