Курсова робота: Метод Ньютона на вирішення нелінійних рівнянь. Чисельні методи розв'язання нелінійних рівнянь. Метод Ньютона для вирішення рівнянь з однією змінною
Федеральне агентство з освіти
Сочинський державний університеттуризму та курортної справи
Факультет інформаційних технологій та математики
Кафедра загальної математики
Курсова роботаз дисципліни
"Чисельні методи"
«Метод Ньютона та його модифікації рішення систем нелінійних рівнянь»
Виконала:
студентка 3 курсу
групи 06-ІНФ
Лавренко М.В.
Перевірив:
доцент, кандидат
педагогічних наук
У зв'язку з розвитком нової обчислювальної технікиінженерна практика наших днів все частіше і частіше зустрічається з математичними завданнями, Точне рішення яких отримати дуже складно чи неможливо. У цих випадках зазвичай вдаються до тих чи інших наближених обчислень. Ось чому наближені та чисельні методи математичного аналізуотримали за Останніми рокамиширокий розвиток і набули винятково важливого значення.
У цій роботі розглядається знаменитий метод Ньютона та його модифікація рішення систем нелінійних рівнянь. Розв'язання систем нелінійних рівнянь – одне із важких завдань обчислювальної математики. Складність полягає в тому, щоб визначити: чи має система рішення, і якщо – так, то скільки. Вивчається збіжність основного та спрощеного методів Ньютона та методу, що отримується з методу Ньютона застосуванням ітераційного процесу для наближеного звернення матриць Якобі.
А також коротко описуються: методи хибного становища, метод січучих, метод Стеффенсена, який частіше виявляється найкращим виборомдля розв'язання систем нелінійних рівнянь ніж метод січень або метод хибного становища.
Знаменитий метод Ньютона є одним з найбільш ефективних методіввирішення різних нелінійних завдань. Розрахункову формулу методу можна одержати, використовуючи різні підходи. Розглянемо два із них.
1) Метод дотичних.
Виведемо розрахункову формулу методу на вирішення нелінійного рівняння
із простих геометричних міркувань. Нехай - задане початкове наближення до кореня. У точці з координатами проведемо дотичну до графіка функції і за нове наближення приймемо абсцис точки перетину цієї дотичної з віссю. Аналогічно за наближення приймемо абсцис точки перетину з віссю дотичної, проведеної до графіка в точці з координатами . Продовжуючи цей процес далі, отримаємо послідовністьРівняння дотичної, проведеної до графіка функції
у точці має вигляд: . (1.1)Вважаючи в рівності (1.1)
, зауважуємо, що з виконанні умови абсцису точки перетину дотичної з віссю задовольняє рівності: . (1.2)Висловлюючи з нього
, отримуємо розрахункову формулу методу Ньютона :Завдяки такій геометричній інтерпретації цей метод часто називають методом дотичних .
Нехай потрібно вирішити систему рівнянь
 (1) - задані, нелінійні (серед них можуть бути і лінійні)
(1) - задані, нелінійні (серед них можуть бути і лінійні) речовиннозначні функції пречових змінних
. Позначивши , ,
, цю систему(2.1) можна записати одним рівнянням
(2)щодо векторної функції Fвекторного аргументу x. Таким чином, вихідне завдання можна розглядати як задачу про нулі нелінійного відображення
У цій постановці вона є прямим узагальненням основного завдання попереднього розділу – завдання побудови методів знаходження нулів одновимірних нелінійних відображень. Фактично це те саме завдання, тільки в просторах більшої розмірності. Тому можна як наново будувати методи її вирішення на основі розроблених вище підходів, так і здійснювати формальне перенесення виведених для скалярного випадку розрахункових формул. У будь-якому випадку слід подбати про правочинність тих чи інших операцій над векторними змінними та векторними функціями, а також про збіжність одержуваних у такий спосіб ітераційних процесів. Часто теореми збіжності цих процесів є тривіальними узагальненнями відповідних результатів, отриманих для методів розв'язання скалярних рівнянь. Однак не всі результати і не всі методи можна перенести з нагоди п= 1 на випадок п≥2. Наприклад, тут уже не працюватимуть методи дихотомії, оскільки безліч векторів не впорядковано. У той же час, перехід від n= 1 до n ≥ 2 вносить у завдання знаходження нулів нелінійного відображення свою специфіку, облік якої призводить до нових методів і різних модифікацій вже наявних. Зокрема, велика варіативність методів вирішення нелінійних систем пов'язана з різноманітністю способів, якими можна вирішувати лінійні завдання алгебри, що виникають при покроковій лінеаризації даної нелінійної вектор-функції. F ( x ).2) Метод лінеаризації.
2. Метод Ньютона розв'язання систем нелінійних рівнянь.
Цей метод має набагато швидшу збіжність, ніж метод простої ітерації. В основі методу Ньютона системи рівнянь (1.1) лежить використання розкладання функцій
 , де
, де  (2.1)
(2.1)
в ряд Тейлора, причому члени, що містять другі і більше високі порядкипохідних, що відкидаються. Такий підхід дозволяє вирішення однієї нелінійної системи(1.1) замінити рішенням низки лінійних систем.
Отже, систему (1.1) вирішуватимемо методом Ньютона. В області D виберемо будь-яку точку  і назвемо її нульовим наближенням до точного рішення вихідної системи. Тепер функції (2.1) розкладемо в ряд Тейлора на околиці точки . Будемо мати
і назвемо її нульовим наближенням до точного рішення вихідної системи. Тепер функції (2.1) розкладемо в ряд Тейлора на околиці точки . Будемо мати
Т.к. ліві частини (2.2) повинні звертатися у нуль згідно з (1.1), то й праві частини (2.2) теж повинні звертатися у нуль. Тому з (2.2) маємо
Усі приватні похідні (2.3) повинні бути обчислені в точці .
(2.3) є система лінійних алгебраїчних рівняньщодо невідомих Цю систему можна вирішити методом Крамера, якщо її основний визначник буде відмінний від нуля та знайти величини
Тепер можна уточнити нульове наближення, побудувавши перше наближення з координатами
тобто.  . (2.6)
. (2.6)
З'ясуємо, чи наближення (2.6) отримано з достатнім ступенем точності. Для цього перевіримо умову
 ,
,  (2.7)
(2.7)
де  наперед задане мале додатне число(точність, з якою має бути вирішена система (1.1)). Якщо умова (2.7) буде виконано, то за наближене рішення системи (1.1) виберемо (2.6) та закінчимо обчислення. Якщо ж умова (2.7) не виконуватиметься, то виконаємо таку дію. У системі (2.3) замість
наперед задане мале додатне число(точність, з якою має бути вирішена система (1.1)). Якщо умова (2.7) буде виконано, то за наближене рішення системи (1.1) виберемо (2.6) та закінчимо обчислення. Якщо ж умова (2.7) не виконуватиметься, то виконаємо таку дію. У системі (2.3) замість  візьмемо уточнені значення
візьмемо уточнені значення
 , (2.8)
, (2.8)
тобто. виконаємо такі дії
 . (2.9)
. (2.9)
Після цього система (2.3) буде системою лінійних рівнянь алгебри щодо величин Визначивши ці величини, наступне друге наближення  до розв'язання системи (1.1) знайдемо за формулами
до розв'язання системи (1.1) знайдемо за формулами
Тепер перевіримо умову (2.7) 
Якщо ця умова виконується, то закінчуємо обчислення, взявши за наближене рішення системи (1.1) друге наближення  . Якщо ж ця умова не виконується, то продовжуємо будувати наступне наближення, прийнявши (2.3)
. Якщо ж ця умова не виконується, то продовжуємо будувати наступне наближення, прийнявши (2.3)  Будувати наближення потрібно доти, доки умова не буде виконана.
Будувати наближення потрібно доти, доки умова не буде виконана.
Робочі формули методу Ньютона на вирішення системи (1.1) можна записати як.
Обчислити послідовність
Тут  є рішенням системи
є рішенням системи
Сформулюємо алгоритм обчислень за формулами (2.11)-(2.13).
1. Виберемо нульове наближення, що належить області D.
2. У системі лінійних рівнянь алгебри (2.13) покладемо  ,а.
,а.
3. Розв'яжемо систему (2.13) і знайдемо величини  .
.
4. У формулах (2.12) покладемо  і обчислимо компоненти наступного наближення.
і обчислимо компоненти наступного наближення.
5. Перевіримо умову (2.7) на : (Див. алгоритм обчислення максимуму кількох величин.)
6. Якщо ця умова виконується, то закінчуємо обчислення, вибравши наближене рішення системи (1.1) наближення . Якщо це умова не виконується, то перейдемо до п.7.
7. Покладемо  для всіх .
для всіх .
8. Виконаємо п.3, поклавши  .
.
Геометрично цей алгоритм можна записати як.

Алгоритм. Обчислення максимуму кількох величин.

приклад. Розглянемо використання методу Ньютона на вирішення системи двох рівнянь.
Методом Ньютона з точністю вирішити наступну систему нелінійних рівнянь
 , (2.14)
, (2.14)
тут  . Виберемо нульове наближення
. Виберемо нульове наближення  , Що належить області D. Побудуємо систему лінійних рівнянь алгебри (2.3). Вона матиме вигляд
, Що належить області D. Побудуємо систему лінійних рівнянь алгебри (2.3). Вона матиме вигляд
 (2.15)
(2.15)
Позначимо
Вирішимо систему (2.15) щодо невідомих  наприклад методом Крамера. Формули Крамера запишемо у вигляді
наприклад методом Крамера. Формули Крамера запишемо у вигляді
 (2.17)
(2.17)
де основний визначник системи (2.15)
 (2.18)
(2.18)
а допоміжні визначники системи (2.15) мають вигляд

 .
.
Знайдені значення підставимо (2.16) і знайдемо компоненти першого наближення  до вирішення системи (2.15).
до вирішення системи (2.15).
Перевіримо умову
 , (2.19)
, (2.19)
якщо це умова виконується, то закінчуємо обчислення, прийнявши за наближене рішення системи (2.15) перше наближення, тобто.  . Якщо умова (2.19) не виконується, то покладемо
. Якщо умова (2.19) не виконується, то покладемо  ,
,  і збудуємо нову системулінійних рівнянь алгебри (2.15). Вирішивши її, знайдемо друге наближення
і збудуємо нову системулінійних рівнянь алгебри (2.15). Вирішивши її, знайдемо друге наближення  . Перевіримо його на . Якщо ця умова виконуватиметься, то за наближене рішення системи (2.15) виберемо
. Перевіримо його на . Якщо ця умова виконуватиметься, то за наближене рішення системи (2.15) виберемо  . Якщо умова не виконуватиметься, покладемо
. Якщо умова не виконуватиметься, покладемо  ,
,  та побудуємо наступну систему (2.15) для знаходження
та побудуємо наступну систему (2.15) для знаходження  і т.д.
і т.д.
Завдання
У всіх завданнях потрібно:
Скласти програму чисельної реалізації методу згідно із запропонованим алгоритмом.
Отримати результати обчислень.
Перевірити отримані результати.
Задано систему двох нелінійних рівнянь.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10.
11.  12.
12. 
13.  14.
14. 
15.  .
.
Глава 3. Чисельні методи розв'язання систем лінійних рівнянь алгебри (СЛАУ).
Мета роботи. Знайомство з деякими наближеними методами рішення СЛАУ та їх чисельною реалізацією на ПК.
Попередні зауваження.Усі методи рішення СЛАУ зазвичай поділяють на великі групи. До першої групи належать методи, які називають точними. Ці методи дозволяють будь-яких систем знайти точні значення невідомих після кінцевого числа арифметичних операцій, кожна з яких виконується точно.
До другої групи відносяться всі методи, які не є точними. Їх називають ітераційними, чи чисельними, чи наближеними. Точне рішення при використанні таких методів виходить в результаті нескінченного процесу наближень. Привабливою рисоютаких методів є їх самовиправність та простота реалізації на ПК.
Розглянемо деякі наближені методи рішення СЛАУ та побудуємо алгоритми їх чисельної реалізації. Наближене рішення СЛАУ будемо отримувати з точністю до , де дуже маленьке позитивне число.
1. Метод ітерації.
Нехай СЛАУ задана у вигляді
 (1.1)
(1.1)
Цю систему можна записати у матричному вигляді
 , (1.2)
, (1.2)
де  - матриця коефіцієнтів при невідомих у системі (1.1),
- матриця коефіцієнтів при невідомих у системі (1.1),  - стовпець вільних членів,
- стовпець вільних членів,  - Стовпець невідомих системи (1.1).
- Стовпець невідомих системи (1.1).
 . (1.3)
. (1.3)
Розв'яжемо систему (1.1) методом ітерації. Для цього виконаємо такі дії.
По перше. Виберемо нульове наближення
 (1.4)
(1.4)
до точного рішення (1.3) системи (1.1). Компонентами нульового наближення можуть бути будь-які числа. Але зручніше компоненти нульового наближення взяти чи нулі  , чи вільні члени системи (1.1)
, чи вільні члени системи (1.1) 
По-друге. Компоненти нульового наближення підставимо в праву частинусистеми (1.1) та обчислимо
 (1.5)
(1.5)
Величини, що стоять зліва (1.5) є компонентами першого наближення  Дії, у яких вийшло перше наближення, називаються ітерацією.
Дії, у яких вийшло перше наближення, називаються ітерацією.
По-третє. Перевіримо нульове та перше наближення на
 (1.6)
(1.6)
Якщо умови (1.6) виконуються, то за наближене рішення системи (1.1) виберемо, або , або однаково, т.к. вони відрізняються один від одного не більше ніж на і закінчимо обчислення. Якщо хоча б одну з умов (1.6) не буде виконано, то перейдемо до наступної дії.
По-четверте. Виконаємо таку ітерацію, тобто. у праву частину системи (1.1) підставимо компоненти першого наближення та обчислимо компоненти другого наближення  , де
, де

У п'ятих. Перевіримо  і , тобто. перевіримо умову (1.6) цих наближень. Якщо умови (1.6) будуть виконані, то за наближене рішення системи (1.1) виберемо, або , або однаково, т.к. вони відрізняються один від одного не більше ніж на . В іншому випадку будуватимемо наступну ітерацію, підставивши компоненти другого наближення в праву частину системи (1.1).
і , тобто. перевіримо умову (1.6) цих наближень. Якщо умови (1.6) будуть виконані, то за наближене рішення системи (1.1) виберемо, або , або однаково, т.к. вони відрізняються один від одного не більше ніж на . В іншому випадку будуватимемо наступну ітерацію, підставивши компоненти другого наближення в праву частину системи (1.1).
Ітерації потрібно будувати доти, доки два сусідні наближення  і відрізнятимуться один від одного не більше, ніж на .
і відрізнятимуться один від одного не більше, ніж на .
Робочу формулуметоду ітерації рішення системи (1.1) можна записати як
Алгоритм чисельної реалізації формули (1.7) може бути таким.

Достатні умовизбіжності методу ітерації для системи (1.1) мають вигляд
1.  , .
, .
2.  ,
,  .
.
3. 
2. Метод простої ітерації.
Нехай система лінійних рівнянь алгебри (СЛАУ) задана у вигляді
 (2.1)
(2.1)
Щоб систему (2.1) вирішити методом простої ітерації, спочатку треба привести до виду
 (2.2)
(2.2)
У системі (2.2)  -ое рівняння є -ое рівняння системи (2.1), дозволене щодо -ой невідомої (
-ое рівняння є -ое рівняння системи (2.1), дозволене щодо -ой невідомої (  ).
).
Метод розв'язання системи (2.1), що полягає у зведенні її до системи (2.2) з наступним рішенням системи (2.2) методом ітерації, називається методом простої ітерації для системи (2.1).
Таким чином, робочі формули методу простої ітерації рішення системи (2.1) матимуть вигляд
 (2.3)
(2.3)
Формули (2.3) можна записати у вигляді
Алгоритм чисельної реалізації методу простої ітерації для системи (2.1) за формулами (2.4) може бути таким.
Цей алгоритм можна записати геометрично.

Достатні умови збіжності методу простої ітерації для системи (2.1) мають вигляд
1.  , .
, .
2.  ,
,  .
.
3. 
3. Стаціонарний метод Зейделя.
Метод Зейделя рішення СЛАУ відрізняється від методу ітерації тим, що знайшовши якесь наближення для тієї компоненти, ми відразу ж використовуємо його для відшукання наступних  ,
,  , …,
, …,  -ий компонент. Такий підхід дозволяє забезпечити вищу швидкість збіжності методу Зейделя проти методом ітерації.
-ий компонент. Такий підхід дозволяє забезпечити вищу швидкість збіжності методу Зейделя проти методом ітерації.
Нехай СЛАУ задана у вигляді
 (3.1)
(3.1)
Нехай  - нульове наближення до точного рішення
- нульове наближення до точного рішення  Системи (3.1). І нехай знайдено
Системи (3.1). І нехай знайдено  -е наближення
-е наближення  . Визначимо компоненти
. Визначимо компоненти  -ого наближення за формулами
-ого наближення за формулами
 (3.2)
(3.2)
Формули (3.2) можна записати у компактному вигляді
 ,
,  ,
,  (3.3)
(3.3)
Алгоритм чисельної реалізації методу Зейделя рішення системи (3.1) за формулами (3.3) може бути таким.
1. Виберемо, наприклад,  ,
, 
2. Покладемо.
3. Для всіх обчислимо.
4. Для всіх перевіримо умови  .
.
5. Якщо всі умови п.4 будуть виконані, то за наближене рішення системи (3.1) виберемо або , або і закінчимо обчислення. Якщо хоча б одна умова у п.4 не буде виконана, перейдемо до п.6.
6. Покладемо та перейдемо до п.3.
Цей алгоритм можна записати геометрично.

Достатня умова збіжності методу Зейделя для системи (3.1) має вигляд  , .
, .
4. Нестаціонарний метод Зейделя.
Цей метод рішення СЛАУ (3.1) забезпечує ще більшу швидкість збіжності методу Зейделя.
Нехай якимось чином для системи (3.1) знайдені компоненти -ого наближення і наближення.
Обчислимо вектор поправки
Підрахуємо величини
 , (4.2)
, (4.2)
Розташуємо величини  , у порядку їх спадання.
, у порядку їх спадання.
У такому порядку перепишемо рівняння в системі (3.1) і невідомі в цій системі. Лінійнаалгебраі нелінійні ... Керівництводлялабораторних робітпо ... методичнівказівки дляпрактичнихробітпо длястудентів ...
Навчальна література (природничі науки та технічні) 2000-2011 цикл опд – 10 років цикл сд – 5 років
Література... Природнінаукив цілому 1. Астрономія [Текст]: посібник для ... Чисельніметоди: Лінійнаалгебраі нелінійні ... Керівництводлялабораторних робітпо ... методичнівказівки дляпрактичнихробітподисципліни "Економіка транспорту" длястудентів ...
- природничі науки (1)
Навчальний посібник... керівництводлястудентівта викладачів, призначене длявикористання не лише при вивченні методівроботи... вироблення практичнихнавичок із використанням реальних даних. Методичнірекомендації повиконання залікової роботиподаному...
- природничі науки - фізико-математичні науки - хімічні науки - науки про землю (геодезичні геофізичні геологічні та географічні науки)
Документ... длястудентівприродно- ... робітподисципліни "Генетика та селекція", присвячених актуальним проблемамцією науки. Систематизовано самостійну роботастудентівпотеоретичному та практичному ... лінійного, нелінійного, динамічний. Усе методи ...
- природничі науки - фізико-математичні науки - хімічні науки - науки про землю (геодезичні геофізичні геологічні та географічні науки) (7)
Список підручниківВизначник Єрьоміна в лінійноїі нелінійноюалгебри : лінійнеі нелінійнепрограмування: новий метод/ Єрьомін, Михайло... Длястудентівта викладачів геологічних спеціальностей вузів. кх-1 1794549 99. Д3 П 693 Практичнекерівництвопо ...
ДЕРЖАВНИЙ ОСВІТНИЙ УСТАНОВА
«Придністровський державний університет ім. Т.Г. Шевченка»
Рибницька філія
Кафедра фізики, математики та інформатики
Курсова робота
з дисципліни: «Практикум щодо вирішення завдань на ЕОМ»
"Метод Ньютона для вирішення нелінійних рівнянь"
Виконала:
студентка ІІІ курсу;
330-ї групи
спеціальності: «Інформатика
з дод. спеціальністю англійська
Ністор А. Р..
Перевірила:
викладач Панченко Т.О.
Впровадження ЕОМ у всі сфери людської діяльності вимагає від фахівців різного профілю оволодіння навичками використання обчислювальної техніки. Підвищується рівень підготовки студентів вузів, які вже з перших курсів долучаються до використання ЕОМ та найпростіших чисельних методів, не кажучи вже про те, при виконанні курсових та дипломних проектів застосування обчислювальної техніки стає нормою в переважній більшості вузів.
Обчислювальна техніка використовується зараз у інженерних розрахунках і економічних науках, а й таких традиційно нематематичних спеціальностях, як медицина, лінгвістика, психологія. У зв'язку з цим можна констатувати, що застосування ЕОМ набуло масового характеру. Виникла численна категорія фахівців – користувачів ЕОМ, яким необхідні знання щодо застосування ЕОМ у своїй галузі – навички роботи з вже наявним програмним забезпеченням, а також створення свого власного програмного забезпечення, пристосованого для вирішення конкретної задачі І тут на допомогу користувачеві приходять описи мов програмування високого рівнята чисельні методи.
Численні методи розробляють та досліджують, як правило, висококваліфіковані фахівці-математики. Для більшості користувачів головним завданням є розуміння основних ідей та методів, особливостей та областей застосування. Однак, користувачі хочуть працювати з ЕОМ не тільки як з високоінтелектуальним калькулятором, а ще і як з помічником повсякденній роботі, сховищем інформації зі швидким та впорядкованим доступом, а також із джерелом та обробником графічної інформації. Всі ці функції сучасної ЕОМ я припускаю продемонструвати у цій роботі.
Цілі і завдання.
Метою даної курсової роботи є вивчення та реалізація в програмному продуктірозв'язання нелінійних рівнянь з допомогою методу Ньютона. Ця роботаскладається з трьох розділів, висновків та додатків. Перший розділ – теоретичний і містить загальні відомостіпро метод Ньютона. Другий – це практична частина. Тут описується метод Ньютона розібраний на конкретні приклади. Третій присвячений тестуванню програми та аналізу результатів. Наприкінці подано висновок про виконану роботу.
Метою даної курсової є програмна реалізація методу Ньютона на вирішення нелінійних рівнянь.
Для цього необхідно виконати такі завдання:
1. Вивчити потрібну літературу.
2. Оглядово розглянути існуючі методиу вирішенні нелінійних рівнянь.
3. Вивчити метод Ньютона на вирішення нелінійних рівнянь.
4. Розглянути рішення нелінійних рівнянь методом Ньютона на конкретних прикладах.
5. Розробити програму на вирішення нелінійних рівнянь методом Ньютона.
6. Проаналізувати результати.
Розглянемо задачу знаходження коріння нелінійного рівняння
Корінням рівняння (1) називаються такі значення х, які при підстановці перетворюють його на тотожність. Тільки найпростіших рівнянь вдається визначити рішення як формул, тобто. аналітичному вигляді. Найчастіше доводиться вирішувати рівняння наближеними методами, найбільшого поширення серед яких, у зв'язку з появою комп'ютерів, набули чисельні методи.
Алгоритм знаходження коренів наближеними методами можна розбити на два етапи. На першому вивчається розташування коренів та проводиться їх поділ. Знаходиться область , де існує корінь рівняння чи початкове наближення до кореня x 0 . Найпростіший спосіброзв'язання цієї задачі є дослідження графіка функції f(x). У випадку для її вирішення необхідно залучати всі засоби математичного аналізу.
Існування на знайденому відрізку принаймні одного кореня рівняння (1) випливає з умови Больцано:
f(a)*f(b)<0 (2)
При цьому мається на увазі, що функція f(x) безперервна на даному відрізку. Однак ця умова не відповідає на питання про кількість коренів рівняння на заданому відрізку. Якщо ж вимогу безперервності функції доповнити ще вимогою її монотонності, але це випливає з знаковості першої похідної , можна стверджувати існування єдиного кореня на заданому відрізку.
При локалізації коренів важливо також знання основних властивостей даного типу рівняння. Наприклад, нагадаємо, деякі властивості рівнянь алгебри:
де речові коефіцієнти.
а) Рівняння ступеня n має n коріння, серед яких можуть бути як речові, так і комплексні. Комплексне коріння утворює комплексно-сполучені пари і, отже, рівняння має парне число таких коренів. При непарному значенні n є щонайменше один речовий корінь.
б) Число позитивних речових коренів менше або дорівнює кількості змінних знаків у послідовності коефіцієнтів. Заміна х на –х у рівнянні (3) дозволяє у такий самий спосіб оцінити кількість негативних коренів.
З другого краю етапі рішення рівняння (1), використовуючи отримане початкове наближення, будується ітераційний процес, що дозволяє уточнювати значення кореня з деякою, наперед заданою точністю . Ітераційний процес полягає у послідовному уточненні початкового наближення. Кожен такий крок називається ітерацією. В результаті процесу ітерації знаходиться послідовність наближених значень коренів рівняння. Якщо ця послідовність зі зростанням n наближається до справжнього значення кореня x, то ітераційний процес сходиться. Кажуть, що ітераційний процес сходиться щонайменше з порядком m, якщо виконано умову:
![]() , (4)
, (4)
де С>0 деяка константа. Якщо m=1 , то говорять про збіжність першого порядку; m=2 - про квадратичну, m=3 - про кубічну збіжність.
Ітераційні цикли закінчуються, якщо за заданої допустимої похибки виконуються критерії по абсолютним чи відносним відхиленням:
або трохи нев'язки:
Ця робота присвячена вивченню алгоритму розв'язання нелінійних рівнянь за допомогою методу Ньютона.
1.1 Огляд існуючих методів розв'язання нелінійних рівнянь
існує багато різних методіввирішення нелінійних рівнянь, деякі з них представлені нижче:
1)Метод ітерацій. При вирішенні нелінійного рівняння методом ітерацій скористаємося записом рівняння як x=f(x). Визначаються початкове значення аргументу x 0 і точність ε. Перше наближення рішення x 1 знаходимо з виразу x 1 = f (x 0), друге - x 2 = f (x 1) і т.д. У загальному випадку i+1 наближення знайдемо за формулою xi+1 = f(xi). Зазначену процедуруповторюємо поки що |f(xi)|>ε. Умова збіжності методу ітерацій | f "(x) |<1.
2)Метод Ньютона. При вирішенні нелінійного рівняння методом Ньтона задаються початкове значення аргументу х 0 і точність ε. Потім у точці (x 0 F (x 0)) проводимо дотичну до графіка F (x) і визначаємо точку перетину дотичної з віссю абсцис x 1 . У точці (x 1 F (x 1)) знову будуємо дотичну, знаходимо наступне наближення шуканого рішення x 2 і т.д. Зазначену процедуру повторюємо поки що |F(xi)| > ε. Для визначення точки перетину (i+1) дотичної з віссю абсцис скористаємося наступною формулою x i+1 =x i -F(xi) F'(xi). Умова збіжності методу дотичних F(x 0)∙F""(x)>0, та ін.
3). Метод дихотомії.Методика рішення зводиться до поступового поділу початкового інтервалу невизначеності навпіл за формулою С к = а к + в к /2.
Для того щоб вибрати з двох відрізків необхідний, треба знаходити значення функції на кінцях відрізків, що виходять, і розглядати той на якому функція буде змінювати свій знак, тобто повинна виконуватися умова f (а к) * f (в к)<0.
Процес розподілу відрізка проводиться до тих пір, поки довжина поточного інтервалу невизначеності не буде меншою за задану точність, тобто
в Як< E. Тогда в качестве приближенного решения уравнения будет точка, соответствующая середине интервала неопределённости.
4). Метод хорд. Ідея методу полягає в тому, що на відрізку будується хорда стягує кінці дуги графіка функції y=f(x), а точка c перетину хорди з віссю абсцис вважається наближеним значенням кореня
c = a - (f(a)Ч (a-b)) / (f(a) - f(b)),
c = b - (f(b)Ч(a-b)) / (f(a) - f(b)).
Наступне наближення шукається на інтервалі або в залежності від символів значень функції в точках a, b, c
x* Про якщо f(с)Ч f(а) > 0 ;
x* Про якщо f(c)Ч f(b)< 0 .
Якщо f"(x) не змінює знак на , то позначаючи c = x 1 і вважаючи початковим наближенням a або b отримаємо ітераційні формули методу хорд із закріпленою правою або лівою точкою.
x 0 =a, x i+1 = x i - f(xi) (b-xi) / (f(b)-f(xi), при f "(x) Ч f "(x) > 0;
x 0 = b, x i + 1 = x i - f (x i) (xi -a) / (f (xi) - f (a), при f "(x) Ч f "(x)< 0 .

Збіжність методу хорд лінійна.
1.2 Алгоритм методу Ньютона
Побудуємо ефективний алгоритм обчислення коренів рівняння. Нехай задано початкове наближення. Обчислимо в цій точці значення функції та її похідної. Розглянемо графічну ілюстрацію методу:
![]() .
.
![]() (8)
(8)
Продовжуючи цей процес, отримаємо відому формулуНьютона:
![]() (9)
(9)

Наведемо найпростішу рекурсивну підпрограму-функцію:
function X_Newt(x,eps:real):real;
y:=x-f(x)/f1(x);
if abs(f(x)) > eps
then X_Newt:=X_Newt(y,eps)
Метод Ньютона (дотичних) характеризується квадратичною швидкістю збіжності, тобто. кожної ітерації подвоюється число вірних символів. Проте це метод який завжди призводить до потрібного результату. Розглянемо це докладніше.
Перетворимо рівняння (1) до еквівалентного рівняння виду:
У разі методу дотичних ![]() . Якщо відомо початкове наближення до кореня x=x 0 то наступне наближення знайдемо з рівняння x 1 =g(x 0), далі x 2 =g(x 1),... Продовжуючи цей процес, отримаємо рекурентну формулу методу простої ітерації
. Якщо відомо початкове наближення до кореня x=x 0 то наступне наближення знайдемо з рівняння x 1 =g(x 0), далі x 2 =g(x 1),... Продовжуючи цей процес, отримаємо рекурентну формулу методу простої ітерації
x k + 1 = g (x k) (11)
Ітераційний процес триває доти, доки не будуть виконані умови (5-7).
Чи завжди описаний обчислювальний процес призводить до шуканого рішення? За яких умов він буде схожим? Для відповіді на ці питання знову звернемося до геометричної ілюстрації методу.
Корінь рівняння є точкою перетину функцій y=x та y=g(x). Як видно із рис. 3(а), якщо виконується умова , процес сходиться, інакше – розходиться (рис3(б)).

Отже, щоб ітераційний процес був схожим і призводив до шуканого результату, потрібно виконання умови:
Перехід від рівняння f(x)=0 до рівняння х=g(x) можна здійснювати у різний спосіб. При цьому важливо, щоб обрана функція g(x) задовольняла умову (12). Наприклад, якщо функцію f(x) помножити довільну константу q і додати до обох частин рівняння (1) змінну х, то g(x)=q*f(x)+x . Виберемо константу q такий, щоб швидкість збіжності алгоритму була найвищою. Якщо 1 Метод Ньютона має високу швидкість збіжності, проте він не завжди сходиться. Умова збіжності , де g(x) = x – f(x)/ f'(x) зводиться до вимоги . У практичних розрахунках важливо вибирати початкове значення якомога ближче до шуканого значення, а в програмі встановлювати запобіжник від зациклювання. Недоліком методу і те, що у кожному кроці необхідно обчислювати як функцію, а й її похідну. Це не завжди зручно. Одна з модифікацій методу Ньютона - обчислення похідної лише першої ітерації: Інший метод модифікації – заміна похідної кінцевої різниці Тоді Геометричний зміст такої зміни алгоритму Ньютона полягає в тому, що від дотичної ми приходимо до січної. Метод січень поступається методу Ньютона у швидкості збіжності, але не вимагає обчислення похідної. Зауважимо, що початкові наближення в методі січучих можуть розташовуватися як з різних боків від кореня, так і з одного боку. Запишемо у вигляді алгоритм методу Ньютона. 1. Задати початкове наближення х (0) так, щоб виконалася умова f(x(0))*f''(x(0))>0. (16) Задати мале позитивне число ε як точність обчислень. Покласти до = 0. 2. Обчислити х (к+1) за формулою (9): 3. Якщо | x(k+1) - x(k) |< ε, то процесс вычисления прекратить и положить х* = x (k+1)
.
Інакше збільшити на 1 (к = до + 1) і перейти до пункту 2. Вирішимо вручну кілька нелінійних рівнянь методом Ньютона, а потім звіримо результати з тими, що вийдуть при реалізації програмного продукту. Приклад 1 sin x 2 + cosx 2 – 10x. = 0. F'(x)=2x cosx 2 - 2x sinx 2 - 10. F''(x)=2cosx 2 - 4x 2 sinx 2 - 2sinx 2 - 4x 2 cosx 2 = cosx 2 (2-4x 2) - sinx 2 (2+4x 2). Тепер, виходячи з графіка, візьмемо перший наближений корінь і перевіримо умову (16): f(x(0)) * f'(x(0)) > 0. Нехай x(0) = 0,565, тоді f(0.565)*f''(0.565) = -4. 387 * (-0. 342) = 1. 5 > 0, Умова виконується, отже беремо x(0) = 0,565. Звідси випливає, що корінь рівняння х = 0,101. Приклад 2 Вирішити рівняння методом Ньютона. cos x - e-x2/2 + x - 1 = 0 Обчислення з точністю ε = 0, 001. Обчислимо першу похідну функції. F'(x) = 1 - sin x + x * e -x2/2. Тепер обчислимо другу похідну функції. F''(x) = e -x2/2 * (1-x 2) - cos x. Побудуємо наближений графік цієї функції. Тепер, виходячи з графіка, візьмемо перший наближений корінь і перевіримо умову (16): f(x(0)) * f'(x(0)) > 0. Нехай x(0) = 2, тоді f(2)*f’’(2) = 0. 449 * 0. 010 = 0.05 > 0, Умова виконується, отже, беремо x(0) = 2. Тепер складемо таблицю значень для вирішення даного рівняння. Звідси випливає, що корінь рівняння х = 1.089. Приклад 3 Вирішити рівняння методом Ньютона. Обчислення з точністю ε = 0, 001. Обчислимо першу похідну функції. F'(x) = 2 * x + e-x. Тепер обчислимо другу похідну функції. F''(x) = 2 - e-x. Побудуємо наближений графік цієї функції. Тепер, виходячи з графіка, візьмемо перший наближений корінь і перевіримо умову (16): f(x(0)) * f'(x(0)) > 0. Нехай x(0) = 1, тоді f(2)*f''(2) = 0. 632 * 1, 632 = 1, 031 > 0, Тепер складемо таблицю значень для вирішення даного рівняння. Звідси випливає, що корінь рівняння х = 0,703. Вирішити рівняння методом Ньютона. cos x -e-x/2 + x-1 = 0. Обчислимо першу похідну функції. F'(x) = -sin x + e-x/2/2+1. Тепер обчислимо другу похідну функції. F''(x) = -cos x - e-x/2/4. Побудуємо наближений графік цієї функції. Тепер, виходячи з графіка, візьмемо перший наближений корінь і перевіримо умову (16): f(x(0)) * f'(x(0)) > 0. Нехай x(0) = 1, тоді f(2)*f''(2) = -0. 066 * (-0.692) = 0. 046 > 0, Умова виконується, отже, беремо x (0) = 1. Тепер складемо таблицю значень для вирішення даного рівняння. Звідси випливає, що корінь рівняння х = 1. 162. Приклад 5 Вирішити рівняння методом Ньютона. 2+e x - e-x = 0. Обчислимо першу похідну функції. F'(x) = e x + e-x. Тепер обчислимо другу похідну функції. F''(x) = e x -e -x. Побудуємо наближений графік цієї функції. Тепер, виходячи з графіка, візьмемо перший наближений корінь і перевіримо умову (16): f(x(0)) * f'(x(0)) > 0. Нехай x(0) = 1, тоді f(2)*f''(2) = 0. 350 * 2, 350 = 0. 823 > 0, Умова виконується, отже, беремо x (0) = 1. Тепер складемо таблицю значень для вирішення даного рівняння. Звідси випливає, що корінь рівняння х = 0,881. Ця програма створена для роботи в текстовому та графічному режимі. Вона складається з модуля Graph, Crt, трьох функцій та трьох процедур. 1. модуль Crt призначений забезпечення контролю над текстовими режимами екрана, розширеними кодами клавіатури, кольорами, вікнами і звуком; 2. модуль Graph призначений забезпечення контролю над графічними об'єктами; 3. procedure GrafInit – ініціалізує графічний режим; 4. function VF - обчислює значення функції; 5. function f1 - обчислює значення першої похідної функції; 6. function X_Newt – реалізує алгоритм розв'язання рівняння методом Ньютона. 7. procedure FGraf – реалізує побудову графіка заданої функції f(x); Ots=35 - константа, визначальна кількість точок для відступу від меж монітора; fmin, fmax – максимальні та мінімальні значення функції; SetColor(4) – процедура, яка встановлює поточний колір графічного об'єкта, використовуючи палітру, даному випадкуце червоний колір; SetBkColor(9) – процедура, яка встановлює поточний колір фону, використовуючи палітру, в даному випадку це світло-синій колір. 8. Procedure MaxMinF – обчислять максимальні та мінімальні значення функції f(x). Line – процедура, яка малює лінію з точки з координатами (x1, у1) у точку з координатами (х2, у2); MoveTo - процедура, що переміщає покажчик (СР) в точку з координатами (х, у); TextColor(5) – процедура, яка встановлює поточний колір символів, у разі – це рожевий; Outtexty(х, у, 'рядок') – процедура, яка виводить рядок, починаючи з позиції (х, у) CloseGraph – процедура, яка закриває графічну систему. Для тестування програми візьмемо приклади, які вирішували в практичній частині роботи, щоб звірити результати та перевірити правильність роботи програми. 1) sin x 2 + cosx 2 – 10x. = 0. Введіть а = -1 Введіть b=1 = [-1, 1] (виведення графіка функції) Отримаємо: х = 0, 0000002 2) cos x - e-x2 / 2 + x - 1 = 0. Ця програма обчислює коріння нелінійного рівняння методом Ньютона з точністю eps і креслить приблизний графік функції на відрізку. Введіть а = -3 Введіть b=3 = [-3, 3] (виведення графіка функції) Корінь рівняння, знайдений методом Ньютона: зробимо перевірку, підставивши отриману відповідь у рівняння. Отримаємо: х=-0, 0000000 3) x 2 - e-x = 0. Ця програма обчислює коріння нелінійного рівняння методом Ньютона з точністю eps і креслить приблизний графік функції на відрізку. Введіть а = -1 Введіть b=1 = [-1, 1] Введіть точність обчислення eps=0. 01 (виведення графіка функції) Корінь рівняння, знайдений методом Ньютона: зробимо перевірку, підставивши отриману відповідь у рівняння. Отримаємо: х = 0, 0000000 4) cos x -e-x / 2 + x-1 = 0. Ця програма обчислює коріння нелінійного рівняння методом Ньютона з точністю eps і креслить приблизний графік функції на відрізку. Введіть а = -1,5 Введіть b=1,5 = [-1,5, 1,5 ] Введіть точність обчислення eps=0. 001 (виведення графіка функції) Корінь рівняння, знайдений методом Ньютона: зробимо перевірку, підставивши отриману відповідь у рівняння. Отримаємо: х = 0, 0008180 5) -2+e x - e-x = 0. Ця програма обчислює коріння нелінійного рівняння методом Ньютона з точністю eps і креслить приблизний графік функції на відрізку. Введіть а = -0,9 Введіть b=0,9 = [-0,9, 0,9] Введіть точність обчислення eps=0. 001 (виведення графіка функції) Корінь рівняння, знайдений методом Ньютона: Зробимо перевірку, підставивши отриману відповідь у рівняння. Метою роботи було створити програму, яка обчислює корінь нелінійного рівняння методом Ньютона. Виходячи з цього, можна зробити висновок, що мети досягнуто, тому що для її здійснення були вирішені такі завдання: 1. Вивчено необхідну літературу. 2.Оглядно розглянуті існуючі методи вирішення нелінійних рівнянь. 3. Вивчений метод Ньютона на вирішення нелінійних рівнянь. 4.Розглянуто рішення нелінійних рівнянь методом Ньютона з прикладу. 5.Проведено тестування та налагодження програми. 1. Б.П. Демидович, І.А Марон. Основи обчислювальної математики. - Москва, вид. "Наука"; 1970. 2. В.М. Вержбицький. Чисельні методи (лінійна алгебра та нелінійні рівняння). - Москва, " вища школа»; 2000. 3. Н.С.Бахвалов, А.В.Лапін, Є.В.Чіжонков. Чисельні методи у завданнях та вправах. - Москва, «Вища школа»; 2000. 4. Метьюз, Джон, Г., Фінк, Куртіс, Д. Чисельні методи MATLAB, 3-е видання. - Москва, «Вільяс»; 2001.![]() (13)
(13)![]() (14)
(14)![]() (15)
(15)![]() .
.
k
x(k)
f(x(k))
f'(x(k))
| x(k+1) - x(k) |
0
0. 565
-4. 387
-9. 982
0. 473
1
0. 092
0. 088
-9. 818
0. 009
2
0. 101
0. 000
-9. 800
0. 000
3
0. 101

k
x(k)
f(x(k))
f'(x(k))
| x(k+1) - x(k) |
0
2
0. 449
0. 361
1. 241
1
-0. 265
0. 881
0. 881
0. 301
2
-0. 021
0. 732
0. 732
0. 029
3
0. 000
0. 716
0. 716
0. 000
4
1. 089

k
x(k)
f(x(k))
f'(x(k))
| x(k+1) - x(k) |
0
1, 000
0, 632
2, 368
0, 267
1
0, 733
0, 057
1, 946
0, 029
2
0, 704
0, 001
1, 903
0, 001
3
0, 703

k
x(k)
f(x(k))
f'(x(k))
| x(k+1) - x(k) |
0
1, 000
-0. 066
0. 462
0. 143
1
1. 161
-0. 007
0. 372
0. 018
2
1. 162
0. 0001.
0. 363
0. 001
3
1. 162

k
x(k)
f(x(k))
f'(x(k))
| x(k+1) - x(k) |
0
1, 000
0, 350
3, 086
0, 114
1
0, 886
0, 013
2, 838
0, 005
2
0, 881
0, 001
2, 828
0, 000
3
0, 881
3.1 Опис програми
3.2 Тестування програми
Список використаної літератури
p align="justify"> Метод Ньютона (також відомий як метод дотичних) - це ітераційний чисельний метод знаходження кореня (нуля) заданої функції. Метод був вперше запропонований англійським фізиком, математиком та астрономом Ісааком Ньютоном (1643-1727), під ім'ям якого і знайшов свою популярність.
Метод був описаний Ісааком Ньютоном у рукописі De analysi per aequationes numero terminorum infinitas (лат .Про баналізі рівняннями нескінченних рядів), адресованої в 1669 Барроу, і в роботі De metodis fluxionum et serierum infinitarum (лат.Метод флюксій і нескінченні ряди) або Geometria analytica ( лат.аналітичнагеометрія) у зборах праць Ньютона, яка була написана у 1671 році. Проте опис методу суттєво відрізнявся від його нинішнього викладу: Ньютон застосовував свій метод виключно поліномам. Він обчислював не послідовні наближення xn, а послідовність поліномів і в результаті отримував наближене рішення x.
Вперше метод був опублікований в трактаті Алгебра Джона Валліса в 1685, на прохання якого він був коротко описаний самим Ньютоном. У 1690 році Джозеф Рафсон опублікував спрощений опис у роботі Analysis aequationum universalis (лат. Загальний аналізрівнянь).Рафсон розглядав метод Ньютона як суто алгебраїчний і обмежив його застосування поліномами, проте при цьому він описав метод на основі послідовних наближень x n замість більш тяжкої для розуміння послідовності поліномів, використаної Ньютоном.
Нарешті, в 1740 метод Ньютона був описаний Томасом Сімпсоном як ітеративний метод першого порядку вирішення нелінійних рівнянь з використанням похідної в тому вигляді, в якому він викладається тут. У тій же публікації Сімпсон узагальнив метод на випадок системи з двох рівнянь і зазначив, що метод Ньютона також може бути застосований для вирішення задач оптимізації шляхом знаходження похідної нуля або градієнта.
Відповідно до даного методу завдання пошуку кореня функції зводиться до задачі пошуку точки перетину з віссю абсцис дотичної, побудованої до графіка функції .
Рис.1 . Графік зміни функції
Проведена в будь-якій точці дотична лінія до графіка функції визначається похідною цієї функції в точці, що розглядається, яка в свою чергу визначається тангенсом кута α (). Точка перетину дотичної з віссю абсцис визначається виходячи з наступного співвідношення прямокутному трикутнику: тангенс кута.у прямокутному трикутнику визначається ставленням протилежного катета до прилеглого катета трикутника. Таким чином, на кожному кроці будується дотична до графіка функції у точці чергового наближення . Крапка перетину дотичної з віссю Ox буде наступною точкою наближення. Відповідно до розглянутого методу розрахунок наближеного значення кореня наi-ітерації проводиться за формулою:
Нахил прямий підлаштовується на кожному кроці найкращим чиномОднак слід звернути увагу на те, що алгоритм не враховує кривизну графіка і отже в процесі розрахунку залишається невідомо в яку сторону може відхилитися графік.
Умовою закінчення ітераційного процесу є виконання наступної умови:
де ˗ допустима похибка визначення кореня.
Метод має квадратичну збіжність. Квадратична швидкість збіжності означає, що кількість вірних знаків у наближеному значенні подвоюється з кожною ітерацією.
Математичне обґрунтування
Нехай дана речова функція, яка визначена і безперервна на ділянці, що розглядається. Необхідно знайти речовий корінь розглянутої функції.
Висновок рівняння заснований на методі простих ітерацій, відповідно до якого рівняння призводять до еквівалентного рівняння за будь-якої функції . Введемо поняття стискаючого відображення, що визначається співвідношенням .
Для найкращої збіжності методу у точці чергового наближення має виконуватися умова. Ця вимогаозначає, що корінь функції повинен відповідати екстремуму функції.
Похідна стискаючого відображеннявизначається у такому вигляді:
Виразимо з цього вираз зміннуза умови прийнятого раніше твердження про те, що за умови необхідно забезпечити умову . В результаті отримаємо вираз для визначення змінної:
З урахуванням цього стискаюча функція прийому наступний вид:
Таким чином алгоритм знаходження чисельного рішення рівняння зводиться до ітераційної процедури обчислення:
Алгоритм знаходження кореня нелінійного рівняння методом
1. Задати початкову точку наближеного значення кореня функції, і навіть похибка розрахунку (мале позитивне число ) і початковий крок ітерації ().
2. Виконати розрахунок наближеного значення кореня функції відповідно до формули:
3. Перевіряємо наближене значення кореня щодо заданої точності, у разі:
Якщо різницю двох послідовних наближень стане менше заданої точності , то ітераційний процес закінчується.
Якщо різниця двох послідовних наближень не досягає необхідної точності, необхідно продовжити ітераційний процес і перейти до п.2 аналізованого алгоритму.
Приклад розв'язування рівнянь
за методомНьютона для рівняння з однією змінною
Як приклад, розглянемо рішення нелінійного рівняння методомНьютона для рівняння з однією змінною. Корінь необхідно знайти з точністю як перший наближення.
Варіант розв'язання нелінійного рівняння у програмному комплексіMathCADпредставлений малюнку 3.
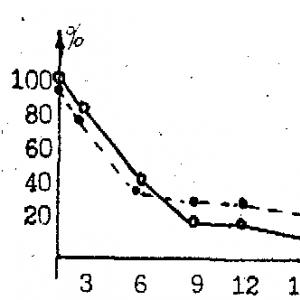
Результати розрахунків, саме динаміка зміни наближеного значення кореня, і навіть похибки розрахунку кроку ітерації представлені у графічній формі (див. рис.2).
Рис.2. Результати розрахунку за методом Ньютона для рівняння з однією змінною
Для забезпечення заданої точності при пошуку наближеного значення кореня рівняння в діапазоні необхідно виконати 4 ітерації. на останньому кроціітерації наближене значення кореня нелінійного рівняння визначатиметься значенням: .
Рис.3 . Лістинг програми вMathCad
Модифікації методу Ньютона для рівняння з однією змінною
Існує кілька модифікацій методу Ньютона, спрямованих спрощення обчислювального процесу.
Спрощений метод Ньютона
Відповідно до методу Ньютона потрібно обчислювати похідну функції f(x) на кожному кроці ітерації, що веде до збільшення обчислювальних витрат. Для зменшення витрат, пов'язаних з обчисленням похідної на кожному кроці розрахунку, можна провести заміну похідної f'(x n ) у точці x n у формулі на похідну f'(x 0) у точці x 0 . Відповідно до даного методу розрахунку наближене значення кореня визначається за такою формулою:Модифікований метод Ньютона
Різнисний метод Ньютона
У результаті наближене значення кореня функції f(x) визначатиметься виразом різницевого методу Ньютона:
Двох кроковий метод Ньютона
Відповідно до методу Ньютона потрібно обчислювати похідну функції f(x) кожному кроці ітерації, що завжди зручно, котрий іноді практично неможливо. Цей спосібдозволяє похідну функції замінити різницевим ставленням (наближеним значенням):
В результаті наближене значення кореня функції f(x) визначатиметься таким виразом:
де
Рис.5 . Двох кроковий метод Ньютона
Метод січучих є дво кроковим, тобто нове наближеннявизначається двома попередніми ітераціямита . У методі необхідно задавати два початкові наближеннята . Швидкість збіжності методу буде лінійною.
- назад
- Вперед
Для того, щоб додати коментар до статті, будь ласка, зареєструйтесь на сайті.
Метод Ньютона (метод дотичних)
Нехай корінь рівняння f(x)=0 відокремлений на відрізку , причому перша та друга похідні f'(x) і f""(x)безперервні та знакопостійні при хÎ.
Нехай на деякому етапі уточнення кореня отримано (вибрано) чергове наближення до кореня х n . Тоді припустимо, що наступне наближення отримане за допомогою поправки h n , призводить до точного значеннякореня
x = х n + h n. (1.2.3-6)
Вважаючи h nмалою величиною, представимо f(х n + h n) у вигляді ряду Тейлора, обмежуючись лінійними доданками
f(хn+hn)» f(хn) + hnf'(хn). (1.2.3-7)
Враховуючи, що f(x) = f(xn + hn) = 0, отримаємо f(xn) + hnf '(xn) »0.
Звідси h n» - f(х n)/f'(х n). Підставимо значення h nв (1.2.3-6) і замість точного значення кореня xотримаємо чергове наближення
Формула (1.2.3-8) дозволяє отримати послідовність наближень x,тобто 
Геометрична інтерпретація методу Ньютонаполягає в наступному
(Рис.1.2.3-6). Приймемо за початкове наближення x 0 правий кінець відрізка b і у відповідній точці 0 на графіку функції y = f(x) побудуємо дотичну. Точка перетину дотичної з віссю абсцис приймається за нове точніше наближення х 1 . Багаторазове повторення цієї процедури дозволяє отримати послідовність наближень х 0 х 1 х 2 , .
.
., яка прагне точного значення кореня x.

Розрахункова формула методу Ньютона (1.2.3-8) можна отримати з геометричного побудови. Так у прямокутному трикутнику х 0 В 0 х 1 катет
х 0 х 1 = х 0 0 /tga. Враховуючи, що точка 0 знаходиться на графіку функції f(x),а гіпотенуза утворена дотичною до графіка f(x) у точці В 0 отримаємо
 (1.2.3-9)
(1.2.3-9)
 (1.2.3-10)
(1.2.3-10)
Ця формула збігається з (1.2.3-8) для n-го наближення.
З рис.1.2.3-6 видно, що вибір як початкового наближення точки а може призвести до того, що наступне наближення х 1 виявиться поза відрізком , на якому відокремлений корінь x. І тут збіжність процесу не гарантована. У загальному випадку вибір початкового наближення здійснюється відповідно до наступним правилом: за початкове наближення слід прийняти таку точку х 0 Î, у якій f(х 0)×f''(х 0)>0, тобто знаки функції та її другий похідний збігаються.
Умови збіжності методу Ньютона сформульовані у наступній теоремі.
Якщо корінь рівняння відокремлений на відрізку, причому f'(х 0)і f''(х) відмінні від нуля і зберігають свої знаки прихÎ, то, якщо вибрати як початкове наближення таку точкух 0 Î , що f(х 0).f¢¢(х 0)>0 , то корінь рівняння f(x)=0 може бути обчислений з будь-яким ступенем точності.
Оцінка похибки методу Ньютона визначається так:
 (1.2.3-11)
(1.2.3-11)
де - найменше значення  при
при 
Процес обчислень припиняється, якщо  ,
,
де - задана точність.
Крім того, умовою досягнення заданої точності при уточненні кореня методом Ньютона можуть бути такі вирази:

Схема алгоритму методу Ньютона наведено на рис. 1.2.3-7.
Ліва частинавихідного рівняння f(x) та її похідна f'(x) в алгоритмі оформлені у вигляді окремих програмних модулів.
Мал. 1.2.3-7. Схема алгоритму методу Ньютона
Приклад 1.2.3-3. Уточнити методом Ньютона корені рівняння x-ln(x+2) = 0 за умови, що коріння цього рівняння відокремлено на відрізках x 1 Î[-1.9;-1.1] та x 2 Î [-0.9;2 ].
Перша похідна f'(x) = 1 – 1/(x+2) зберігає свій знак кожному з відрізків:
f’(x)<0 при хÎ [-1.9; -1.1],
f’(x)>0 при хÎ [-0.9; 2].
Друга похідна f"(x) = 1/(x+2) 2 > 0 за будь-яких х.
Отже, умови збіжності виконуються. Оскільки f""(x)>0на всій області допустимих значень, то для уточнення кореня за початкове наближення x 1виберемо х 0 =-1,9 (оскільки f(-1,9)×f”(-1.9)>0). Отримаємо послідовність наближень:

Продовжуючи обчислення, отримаємо наступну послідовність перших чотирьох наближень: -1.9; -1.8552, -1.8421; -1.8414 . Значення функції f(x) у точці x=-1.8414 дорівнює f(-1.8414)=-0.00003 .
Для уточнення кореня x 2 Î[-0.9;2] виберемо як початкове наближення 0 =2 (f(2)×f”(2)>0). З х 0 = 2, отримаємо послідовність наближень: 2.0;1.1817; 1.1462; 1.1461. Значення функції f(x) у точці x=1.1461 дорівнює f(1.1461)=-0.00006.
Метод Ньютона має високу швидкість збіжності, проте кожному кроці він вимагає обчислення як значення функції, а й її похідної.
Метод хорд
Геометрична інтерпретація методу хордполягає в наступному
(Рис.1.2.3-8).

Проведемо відрізок прямої через точки A та B. Чергове наближення x 1 є абсцисою точки перетину хорди з віссю 0х. Побудуємо рівняння відрізка прямої:

Покладемо y=0і знайдемо значення х=х 1 (чергове наближення):

Повторимо процес обчислень для отримання чергового наближення до кореня - х 2 :

У разі (рис.1.2.11)  і розрахункова формула методу хорд матиме вигляд
і розрахункова формула методу хорд матиме вигляд
Ця формула справедлива, коли за нерухому точку приймається точка b, а як початкове наближення виступає точка a.
Розглянемо інший випадок (рис. 1.2.3-9), коли  .
.
 |
Рівняння прямої для цього випадку має вигляд

Чергове наближення х 1 за y = 0

Тоді рекурентна формула методу хорд для цього випадку має вигляд
Слід зазначити, що за нерухому точку методу хорд вибирають той кінець відрізка , для якого виконується умова f (x)∙f¢¢ (x)>0.
Таким чином, якщо за нерухому точку прийняли точку а , то як початкове наближення виступає х 0 = b, і навпаки.
Достатні умови, які забезпечують обчислення кореня рівняння f(x)=0 за формулою хорд, будуть тими самими, що й методу дотичних (метод Ньютона), тільки замість початкового наближення вибирається нерухома точка. Метод хорд є модифікацією методу Ньютона. Різниця полягає в тому, що як чергове наближення в методі Ньютона виступає точка перетину дотичної з віссю 0Х, а в методі хорд - точка перетину хорди з віссю 0Х - наближення сходяться до кореня з різних сторін.
Оцінка похибки методу хорд визначається виразом
 (1.2.3-15)
(1.2.3-15)
Умова закінчення процесу ітерацій за методом хорд
 (1.2.3-16)
(1.2.3-16)
Якщо M 1<2m 1 , то для оценки погрешности метода может быть использована формула | x n -x n -1 |£e.
Приклад 1.2.3-4. Уточнити корінь рівняння e x - 3x = 0, відокремлений на відрізку з точністю 10 -4.
Перевіримо умову збіжності:

Отже, за нерухому точку слід вибрати а=0, а як початкове наближення прийняти х 0 =1, оскільки f(0)=1>0 і f(0)*f"(0)>0.

 при
при