Власний векторний визначення. Власні числа та власні вектори матриці

Як вставити математичні формулина сайт?

Якщо потрібно колись додавати одну-дві математичні формули на веб-сторінку, то найпростіше зробити це, як описано в статті: математичні формули легко вставляються на сайт у вигляді картинок, які автоматично генерує Вольфрам Альфа. Крім простоти, цей універсальний спосіб допоможе покращити видимість сайту пошукових системах. Він працює давно (і, гадаю, працюватиме вічно), але морально вже застарів.

Якщо ви постійно використовуєте математичні формули на своєму сайті, я рекомендую вам використовувати MathJax - спеціальну бібліотеку JavaScript, яка відображає математичні позначення у веб-браузерах з використанням розмітки MathML, LaTeX або ASCIIMathML.

Є два способи, як почати використовувати MathJax: (1) за допомогою простого коду можна швидко підключити до вашого сайту скрипт MathJax, який автоматично підвантажуватиметься з віддаленого сервера (список серверів); (2) завантажити скрипт MathJax з віддаленого сервера на свій сервер та підключити до всіх сторінок свого сайту. Другий спосіб – більш складний та довгий – дозволить прискорити завантаження сторінок вашого сайту, і якщо батьківський сервер MathJax з якихось причин стане тимчасово недоступним, це ніяк не вплине на ваш власний сайт. Незважаючи на ці переваги, я вибрав перший спосіб, як більш простий, швидкий і не потребує технічних навичок. Наслідуйте мій приклад, і вже через 5 хвилин ви зможете використовувати всі можливості MathJax на своєму сайті.

Підключити скрипт бібліотеки MathJax з віддаленого сервера можна за допомогою двох варіантів коду, взятого на головному сайті MathJax або на сторінці документації:

Один з цих варіантів коду потрібно скопіювати і вставити в код вашої веб-сторінки, бажано між тегами або відразу після тега . За першим варіантом MathJax підвантажується швидше і менше гальмує сторінку. Натомість другий варіант автоматично відстежує та підвантажує свіжі версії MathJax. Якщо вставити перший код, його потрібно буде періодично оновлювати. Якщо вставити другий код, то сторінки завантажуватимуться повільніше, зате вам не потрібно буде постійно стежити за оновленнями MathJax.

Підключити MathJax найпростіше в Blogger або WordPress: в панелі керування сайтом додайте віджет, призначений для вставки стороннього коду JavaScript, скопіюйте в нього перший або другий варіант коду завантаження, представленого вище, і розмістіть віджет ближче до початку шаблону (до речі, це зовсім не обов'язково , оскільки скрипт MathJax завантажується асинхронно). От і все. Тепер вивчіть синтаксис розмітки MathML, LaTeX та ASCIIMathML, і ви готові вставляти математичні формули на веб-сторінки свого сайту.

Будь-який фрактал будується по певному правилу, Яке послідовно застосовується необмежену кількість разів. Щоразу називається ітерацією.

Ітеративний алгоритм побудови губки Менгера досить простий: вихідний куб зі стороною 1 ділиться площинами, що паралельні його граням, на 27 рівних кубів. З нього видаляються один центральний куб і 6 прилеглих до нього на грані кубів. Виходить безліч, що складається з 20 менших кубів, що залишилися. Поступаючи так само з кожним із цих кубів, отримаємо безліч, що складається вже з 400 менших кубів. Продовжуючи цей процес безкінечно, отримаємо губку Менгера.

Найбільш просто влаштовані матриці діагонального вигляду. Виникає питання, чи не можна знайти базис, у якому матриця лінійного оператора мала б діагональний вигляд. Такий базис існує.
Нехай дано лінійний простір R n і лінійний оператор A, що діє в ньому; у цьому випадку оператор A переводить R n у себе, тобто A: R n → R n .

Визначення. Ненульовий вектор називається власним вектором оператора A якщо оператор A переводить в колінеарний йому вектор, тобто . Число λ називається власним значенням або власним числом оператора A, що відповідає власному вектору.
Зазначимо деякі властивості власних чисел та власних векторів.
1. Будь-яка лінійна комбінація власних векторів оператора A, відповідальних одному й тому власному числу λ, є власним вектором з тим самим власним числом.
2. Власні вектори оператора A з попарно різними власними числами λ 1 , λ 2 , …, λ m лінійно незалежні.
3. Якщо власні числа λ 1 =λ 2 = λ m = λ, то власному числу λ відповідає не більше m лінійно незалежних власних векторів.

Отже, якщо є n лінійно незалежних власних векторів , відповідних різним власним числам λ 1 , λ 2 , …, λ n , всі вони лінійно незалежні, отже, їх можна вважати базис простору R n . Знайдемо вид матриці лінійного оператора A у базисі з його власних векторів, для чого подіємо оператором A на базисні вектори: тоді .
Таким чином, матриця лінійного оператора A в базисі його власних векторів має діагональний вигляд, причому по діагоналі стоять власні числа оператора A.
Чи існує інший базис, у якому матриця має діагональний вигляд? Відповідь на поставлене запитання дає така теорема.

Теорема. Матриця лінійного оператора A у базисі (i = 1..n) має діагональний вигляд тоді і лише тоді, коли всі вектори базису - власні вектори оператора A.

Правило відшукання власних чисел і власних векторів Нехай дано вектор , де x 1 x 2 … x n - координати вектора щодо базису і - власний вектор лінійного оператора A, що відповідає власному числу , тобто . Це співвідношення можна записати у матричній формі

. (*)

Рівняння (*) можна як рівняння для відшукання , причому , тобто нас цікавлять нетривіальні рішення, оскільки власний вектор може бути нульовим. Відомо, що нетривіальні рішення однорідної системи лінійних рівняньіснують тоді і тільки тоді, коли det(A - E) = 0. Таким чином, для того, щоб λ було власним числом оператора A необхідно і достатньо, щоб det(A - E) = 0.
Якщо рівняння (*) докладно розписати в координатній формі, то отримаємо систему лінійних однорідних рівнянь:

(1)
де - матриця лінійного оператора.

Система (1) має ненульове рішення, якщо її визначник D дорівнює нулю

Здобули рівняння для знаходження власних чисел.
Це рівняння називається характеристичним рівнянням, яке ліва частина- характеристичним многочленом матриці (оператора) A. Якщо характеристичний многочлен немає речових коренів, то матриця A немає власних векторів і його не можна призвести до діагональному виду.
Нехай λ 1 , λ 2 , …, λ n - речові корені характеристичного рівняння, причому серед них можуть бути і кратні. Підставляючи по черзі ці значення систему (1), знаходимо власні вектори.

Приклад 12 Лінійний оператор A діє в R 3 згідно із законом , де x 1 , x 2 ,.., x n - координати вектора в базисі , , . Знайти власні числа та власні вектори цього оператора.
Рішення. Будуємо матрицю цього оператора:
.
Складаємо систему визначення координат власних векторів:

Складаємо характеристичне рівнянняі вирішуємо його:

.
λ 1,2 = -1, λ 3 = 3.
Підставляючи λ = -1 у систему, маємо:
або
Так як , то залежних змінних два, а вільне одне.
Нехай x 1 - вільне невідоме, тоді Вирішуємо цю систему будь-яким способом і знаходимо загальне рішенняцієї системи: Фундаментальна системарішень складається з одного рішення, оскільки n – r = 3 – 2 = 1.
Безліч власних векторів, що відповідають своєму числу λ = -1, має вигляд: , де x 1 - будь-яке число, відмінне від нуля. Виберемо з цієї множини один вектор, наприклад, поклавши x 1 = 1: .
Розмірковуючи аналогічно, знаходимо власний вектор, що відповідає власному числу = 3: .
У просторі R 3 базис складається з трьох лінійно незалежних векторів, ми отримали тільки два лінійно незалежних власних вектора, з яких базис в R 3 скласти не можна. Отже, матрицю A лінійного оператора призвести до діагонального вигляду не можемо.

приклад 13. Дана матриця .
1. Довести, що вектор є власним вектором матриці A. Знайти власне число, що відповідає цьому власному вектору.
2. Знайти базис, у якому матриця A має діагональний вигляд.
Рішення.
1. Якщо , то - власний вектор

.
Вектор (1, 8, -1) – власний вектор. Власне число = -1.
Діагональний вигляд матриця має в базисі, що складається зі своїх векторів. Один із них відомий. Знайдемо решту.
Власні вектори шукаємо із системи:

Характеристичне рівняння: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Знайдемо власний вектор, що відповідає власному числу = -3:

Ранг матриці цієї системи дорівнює двом і дорівнює числу невідомих, тому ця система має тільки нульове рішення x 1 = x 3 = 0. x 2 тут може бути будь-яким, відмінним від нуля, наприклад, x 2 = 1. Таким чином, вектор (0 ,1,0) є власним вектором, що відповідає λ = -3. Перевіримо:
.
Якщо λ = 1, то одержуємо систему
Ранг матриці дорівнює двом. Останнє рівняння викреслюємо.
Нехай x 3 – вільне невідоме. Тоді x 1 = -3 x 3, 4 x 2 = 10 x 1 - 6 x 3 = -30 x 3 - 6 x 3, x 2 = -9 x 3.
Вважаючи x 3 = 1, маємо (-3,-9,1) - власний вектор, що відповідає власному числу λ = 1. Перевірка:

.
Так як власні числа дійсні і різні, то вектори, що їм відповідають, лінійно незалежні, тому їх можна прийняти за базис R 3 . Таким чином, у базисі , , матриця A має вигляд:
.
Не будь-яку матрицю лінійного оператора A:R n → R n можна призвести до діагонального вигляду, оскільки для деяких лінійних операторів лінійно незалежних власних векторів може бути менше n. Однак, якщо матриця симетрична, кореню характеристичного рівняння кратності m відповідає рівно m лінійно незалежних векторів.

Визначення. Симетричною матрицею називається квадратна матриця, В якій елементи, симетричні щодо головної діагоналі, рівні, тобто в якій .
Зауваження. 1. Усі власні числа симетричної матриці речові.
2. Власні вектори симетричної матриці, що відповідають попарно різним власним числам, ортогональні.
Як один з численних додатків вивченого апарату, розглянемо завдання визначення виду кривої другого порядку.

Визначення 9.3.Вектор хназивається власним вектором матриці Аякщо знайдеться таке число λ, що виконується рівність: Ах = λх,тобто результатом застосування до хлінійного перетворення, що задається матрицею А, є множення цього вектора на число λ . Саме число λ називається власним числом матриці А.

Підставивши формули (9.3) x` j = λx j ,отримаємо систему рівнянь визначення координат власного вектора:

. (9.5)

Ця лінійна однорідна системабуде мати нетривіальне рішеннялише у разі, якщо її головний визначник дорівнює 0 (правило Крамера). Записавши цю умову у вигляді:

отримаємо рівняння для визначення власних чисел λ , що називається характеристичним рівнянням . Коротко його можна уявити так:

| A - λE | = 0, (9.6)

оскільки в його лівій частині стоїть визначник матриці А-λЕ. Багаточлен щодо λ | A - λE| називається характеристичним багаточленом матриці А.

Властивості характеристичного багаточлена:

1) Характеристичний многочлен лінійного перетворення залежить від вибору базису. Доведення. (див. (9.4)), але отже, . Таким чином, не залежить від вибору базису. Отже, та | A-λE| не змінюється під час переходу до нового базису.

2) Якщо матриця Алінійного перетворення є симетричною (тобто. а ij = a ji), то всі коріння характеристичного рівняння (9.6) – дійсні числа.

Властивості власних чисел та власних векторів:

1) Якщо вибрати базис із власних векторів х 1, х 2, х 3, що відповідають власним значенням λ 1 , λ 2 , λ 3матриці А, то цьому базисі лінійне перетворення А має матрицю діагонального виду:

(9.7) Доказ цієї якості випливає з визначення власних векторів.

2) Якщо власні значення перетворення Арізні, відповідні їм власні вектори лінійно незалежні.

3) Якщо характеристичний багаточлен матриці Амає три різні корені, то в деякому базисі матриця Амає діагональний вигляд.

Знайдемо власні числа та власні вектори матриці Складемо характеристичне рівняння: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Знайдемо координати власних векторів, які відповідають кожному знайденому значенню λ. З (9.5) випливає, що якщо х (1) ={x 1 x 2 x 3) – власний вектор, відповідний λ 1 =-2, то

- Спільна, але невизначена система. Її рішення можна записати у вигляді х (1) ={a,0,-a), де а - будь-яке число. Зокрема, якщо вимагати, щоб | x (1) |=1, х (1) =

Підставивши систему (9.5) λ 2 =3, отримаємо систему визначення координат другого власного вектора - x (2) ={y 1 ,y 2 ,y 3}:

, звідки х (2) ={b,-b,b) або, за умови | x (2) |=1, x (2) =

Для λ 3 = 6 знайдемо власний вектор x (3) ={z 1 , z 2 , z 3}:

, x (3) ={c,2c,c) або в нормованому варіанті

х (3) = Можна помітити, що х (1) х (2) = ab – ab= 0, x (1) x (3) = ac – ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Таким чином, власні вектори цієї матриці попарно ортогональні.

лекція 10.

Квадратичні форми та їх зв'язок із симетричними матрицями. Властивості власних векторів та власних чисел симетричної матриці. Приведення квадратичної форми до канонічного вигляду.

Визначення 10.1.Квадратичною формою дійсних змінних х 1, х 2, ..., х nназивається многочлен другого ступеня щодо цих змінних, що не містить вільного члена та членів першого ступеня.

Приклади квадратичних форм:

(n = 2),

(n = 3). (10.1)

Нагадаємо дане в минулій лекції визначення симетричної матриці:

Визначення 10.2.Квадратна матриця називається симетричною, якщо, тобто якщо рівні елементи матриці, симетричні щодо головної діагоналі.

Властивості власних чисел та власних векторів симетричної матриці:

1) Усі власні числа симетричної матриці дійсні.

Доказ (для n = 2).

Нехай матриця Амає вигляд: . Складемо характеристичне рівняння:

(10.2) Знайдемо дискримінант:

Отже, рівняння має лише дійсне коріння.

2) Власні вектори симетричної матриці ортогональні.

Доказ (для n= 2).

Координати власних векторів повинні задовольняти рівнянням.

У першій частині викладено положення, мінімально необхідні для розуміння хемометрики, а в другій частині - факти, які необхідно знати для більш глибокого розуміння методів багатовимірного аналізу. Виклад ілюструється прикладами, виконаними в робочій книзі Excel Matrix.xls, що супроводжує цей документ.

Посилання на приклади розміщені в тексті як об'єкти Excel. Ці приклади мають абстрактний характер, вони не прив'язані до завдань аналітичної хімії. Реальні прикладиВикористання матричної алгебри в хемометриці розглянуті в інших текстах, присвячених різноманітним хемометричним додаткам.

Більшість вимірів, які проводяться в аналітичній хімії, є не прямими, а непрямими. Це означає, що в експерименті замість значення шуканого аналіту C (концентрації) виходить інша величина x(Сигнал), пов'язана, але не рівна C, тобто. x(C) ≠ С. Як правило, вид залежності x(C) не відомий, однак, на щастя, в аналітичній хімії більшість вимірів пропорційні. Це означає, що при збільшенні концентрації С aраз, сигнал X збільшиться стільки ж., тобто. x(a C) = a x(C). Крім того, сигнали ще й адитивні, так що сигнал від проби, в якій присутні дві речовини з концентраціями C 1 і C 2 буде дорівнює сумісигналів кожного компонента, тобто. x(C 1 + C 2) = x(C 1)+ x(C 2). Пропорційність та адитивність разом дають лінійність. Можна навести багато прикладів, що ілюструють принцип лінійності, але досить згадати два самих яскравих прикладів- хроматографію та спектроскопію. Друга особливість, властива експерименту в аналітичній хімії – це багатоканальність. Сучасне аналітичне обладнання одночасно вимірює сигнали багатьох каналів. Наприклад, вимірюється інтенсивність пропускання світла одночасно кількох довжин хвиль, тобто. Спектр. Тому в експерименті ми маємо справу з безліччю сигналів x 1 , x 2 ,...., x n , що характеризують набір концентрацій C 1 ,C 2 , ..., C m речовин, присутніх в системі, що вивчається.

Мал. 1 Спектри

Отже, аналітичний експеримент характеризується лінійністю та багатовимірністю. Тому зручно розглядати експериментальні дані як вектори та матриці та маніпулювати з ними, використовуючи апарат матричної алгебри. Плідність такого підходу ілюструє приклад, показаний на де представлені три спектри, зняті для 200 довжин хвиль від 4000 до 4796 cm -1 . Перший (x 1) і другий (x 2) спектри отримані для стандартних зразків, у яких концентрація двох речовин A і B відомі: у першому зразку [A] = 0.5, [B] = 0.1, а в другому зразку [A] = 0.2, [B] = 0.6. Що можна сказати про новий, невідомий зразок, спектр якого позначений x 3?

Розглянемо три експериментальних спектри x 1 , x 2 і x 3 як три вектори розмірності 200. Засобами лінійної алгебри можна легко показати, що x 3 = 0.1 x 1 +0.3 x 2 тому у третьому зразку очевидно присутні тільки речовини A і B в концентраціях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 та [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Базові відомості 1.1 Матриці

Матрицеюназивається прямокутна таблиця чисел, наприклад

Мал. 2 Матриця

Матриці позначаються великими напівжирними літерами (A ), які елементи - відповідними малими літерамиіз індексами, тобто. a ij. Перший індекс нумерує рядки, а другий – стовпці. У хемометриці прийнято позначати максимальне значенняіндексу тієї ж літерою, як і сам індекс, але великої. Тому матрицю A можна також записати як ( a ij , i = 1,..., I; j = 1,..., J). Для наведеної у прикладі матриці I = 4, J= 3 і a 23 = −7.5.

Пара чисел Iі Jназивається розмірністю матриці та знається як I× J. Прикладом матриці в хемометриці може бути набір спектрів, отриманий для Iзразків на Jдовжини хвиль.

1.2. Найпростіші операції з матрицями

Матриці можна множити на числа. У цьому кожен елемент множиться цього числа. Наприклад -

Мал. 3 Розмноження матриці на число

Дві матриці однакової розмірності можна поелементно складатиі віднімати. Наприклад,

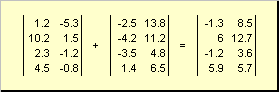
Мал. 4 Додавання матриць

В результаті множення на число та додавання виходить матриця тієї ж розмірності.

Нульовою матрицею називається матриця, що складається з нулів. Вона позначається O. Вочевидь, що A +O = A , A −A = O і 0A = O .

Матрицю можна транспонувати. У цій операції матриця перевертається, тобто. рядки та стовпці змінюються місцями. Транспонування позначається штрихом, A " або індексом A t. Таким чином, якщо A = ( a ij , i = 1,..., I; j = 1,...,J), то A t = ( a ji , j = 1,...,J; i = 1,..., I). Наприклад

Мал. 5 Транспонування матриці

Очевидно, що (A t) t = A, (A + B) t = A t + B t.

1.3. Розмноження матриць

Матриці можна перемножуватиале тільки в тому випадку, коли вони мають відповідні розмірності. Чому це так, буде ясно з визначення. Добутком матриці A , розмірністю I× K, та матриці B , розмірністю K× J, називається матриця C розмірністю I× J, елементами якої є числа

Таким чином для добутку AB необхідно, щоб число стовпців у лівій матриці A дорівнювало числу рядків у правій матриці B . Приклад твору матриць -

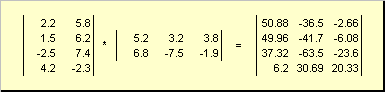
Рис.6 Добуток матриць

Правило перемноження матриць можна сформулювати так. Для того, щоб знайти елемент матриці C , що стоїть на перетині i-ого рядка та j-ого стовпця ( c ij) треба поелементно перемножити i-у рядок першої матриці A на jстовпець другої матриці B і скласти всі результати. Так у наведеному прикладі, елемент з третього рядка та другого стовпця, виходить як сума поелементних творів третього рядка A та другого стовпця B

Рис.7 Елемент твору матриць

Добуток матриць залежить від порядку, тобто. AB ≠ BA , хоча б з міркувань розмірності. Говорять, що воно некомутативно. Однак добуток матриць асоціативний. Це означає, що ABC = (AB) C = A (BC). З іншого боку, воно ще й дистрибутивно, тобто. A (B + C) = AB + AC. Очевидно, що AO = O.

1.4. Квадратні матриці

Якщо число стовпців матриці дорівнює числу її рядків ( I = J = N), то така матриця називається квадратною. У цьому розділі ми розглядатимемо лише такі матриці. Серед цих матриць можна виділити матриці, що мають особливі властивості.

Одиничноюматрицею (позначається I, котрий іноді E ) називається матриця, яка має всі елементи рівні нулю, крім діагональних, які рівні 1, тобто.

Вочевидь AI = IA = A .

Матриця називається діагональної, якщо всі її елементи, крім діагональних ( a ii) Дорівнюють нулю. Наприклад

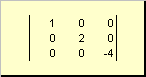
Мал. 8 Діагональна матриця

Матриця A називається верхньою трикутної, якщо її елементи, лежачі нижче діагоналі, дорівнюють нулю, тобто. a ij= 0, при i>j. Наприклад

Мал. 9 Верхня трикутна матриця

Аналогічно визначається нижня трикутна матриця.

Матриця A називається симетричноюякщо A t = A . Іншими словами a ij = a ji. Наприклад

Мал. 10 Симетрична матриця

Матриця A називається ортогональна, якщо

A t A = AA t = I.

Матриця називається нормальноюякщо

1.5. Слід та визначник

Слідомквадратної матриці A (позначається Tr(A ) або Sp(A )) називається сума її діагональних елементів,

Наприклад,

Мал. 11 Слід матриці

Очевидно, що

Sp(α A ) = α Sp(A ) та

Sp (A + B) = Sp (A) + Sp (B).

Можна показати, що

Sp(A ) = Sp(A t), Sp(I ) = N,

а також, що

Sp(AB) = Sp(BA).

Інший важливою характеристикоюквадратної матриці є її визначник(позначається det(A)). Визначення визначника в загальному випадкудосить складно, тому ми почнемо з найпростішого варіанта – матриці A розмірністю (2×2). Тоді

Для матриці (3×3) визначник дорівнюватиме

У разі матриці ( N× N) визначник обчислюється як сума 1 · 2 · 3 · ... · N= N! доданків, кожен з яких дорівнює

Індекси k 1 , k 2 ,..., k Nвизначаються як всілякі впорядковані перестановки rчисел у наборі (1, 2, ... , N). Обчислення визначника матриці – це складна процедура, яку практично здійснюється за допомогою спеціальних програм. Наприклад,

Мал. 12 Визначник матриці

Відзначимо лише очевидні властивості:

det(I ) = 1, det(A ) = det(A t),

det(AB) = det(A)det(B).

1.6. Вектори

Якщо матриця складається лише з одного стовпця ( J= 1), то такий об'єкт називається вектором. Точніше, вектором-стовпцем. Наприклад

Можна розглядати і матриці, що складаються з одного рядка, наприклад

Цей об'єкт також є вектором, але вектор-рядок. При аналізі даних важливо розуміти, з якими векторами ми маємо справу – зі стовпцями чи рядками. Так спектр, знятий одного зразка можна як вектор-рядок. Тоді набір спектральних інтенсивностей на якійсь довжині хвилі для всіх зразків слід трактувати як вектор-стовпець.

Розмірністю вектора називається кількість його елементів.

Зрозуміло, кожен вектор-стовпець можна перетворити на вектор-рядок транспонуванням, тобто.

У тих випадках, коли форма вектора спеціально не обговорюється, а просто говориться вектор, то мають на увазі вектор-стовпець. Ми також дотримуватимемося цього правила. Вектор позначається малою прямою напівжирною літерою. Нульовим вектором називається вектор, всі елементи якого рани нулю. Він позначається 0 .

1.7. Найпростіші операції з векторами

Вектори можна складати і множити числа так само, як це робиться з матрицями. Наприклад,

Мал. 13 Операції з векторами

Два вектори x та y називаються колінеарнимиякщо існує таке число α, що

1.8. Твори векторів

Два вектори однакової розмірності Nможна перемножити. Нехай є два вектори x = ( x 1 , x 2 ,...,x N) t та y = ( y 1 , y 2 ,...,y N) t. Керуючись правилом перемноження "рядок на стовпець", ми можемо скласти з них два твори: x t y та xy t . Перший твір

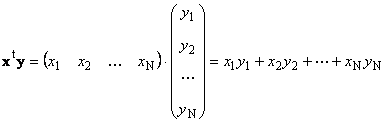
називається скалярнимабо внутрішнім. Його результат – це число. Для нього також використовується позначення (x, y) = x t y. Наприклад,

Мал. 14 Внутрішній (скалярний) твір

Другий твір

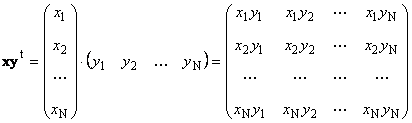
називається зовнішнім. Його результат – це матриця розмірності ( N× N). Наприклад,

Мал. 15 Зовнішній твір

Вектор, скалярний добутокяких одно нулю, називаються ортогональними.

1.9. Норма вектора

Скалярний добуток самого себе називається скалярним квадратом. Ця величина

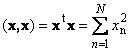
визначає квадрат довжинивектора x. Для позначення довжини (названої також нормоювектора) використовується позначення

Наприклад,

Мал. 16 Норма вектора

Вектор одиничної довжини (||x || = 1) називається нормованим. Ненульовий вектор (x ≠ 0 ) можна унормувати, розділивши його на довжину, тобто. x = | | x | | (x/ ||x ||) = ||x || e. Тут e = x/ | | x | | - Нормований вектор.

Вектори називаються ортонормованими, якщо всі вони нормовані та попарно ортогональні.

1.10. Кут між векторами

Скалярний твір визначає і кутφ між двома векторами x та y

Якщо вектори ортогональні, то cosφ = 0 і φ = π/2, а якщо вони колінеарні, то cosφ = 1 та φ = 0.

1.11. Векторне подання матриці

Кожну матрицю розміру A I× Jможна подати як набір векторів

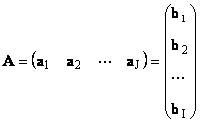
Тут кожен вектор a jє j-им стовпцем, а вектор-рядок b iє i-им рядком матриці A

1.12. Лінійно залежні вектори

Вектори однакової розмірності ( N) можна складати та множити на число, також як матриці. В результаті вийде вектор тієї ж розмірності. Нехай є кілька векторів однієї розмірності x 1 , x 2 ,...,x K і стільки ж чисел α α 1 , α 2 ,...,α K. Вектор

y = α 1 x 1 + α 2 x 2 +...+ α K x K

називається лінійною комбінацієювекторів x k .

Якщо є такі ненульові числа α k ≠ 0, k = 1,..., K, Що y = 0, то такий набір векторів x kназивається лінійно залежним. Інакше вектори називаються лінійно незалежними. Наприклад, вектори x 1 = (2, 2) t та x 2 = (−1, −1) t лінійно залежні, т.к. x 1 +2x 2 = 0

1.13. Ранг матриці

Розглянемо набір з Kвекторів x 1 , x 2 ,...,x Kрозмірності N. Ранг цієї системи векторів називається максимальне число лінійно-незалежних векторів. Наприклад у наборі

є тільки два лінійно незалежних вектор, Наприклад x 1 і x 2 тому її ранг дорівнює 2.

Очевидно, що якщо векторів у наборі більше, ніж їх розмірність ( K>N), то вони обов'язково лінійно залежні.

Рангом матриці(позначається rank(A)) називається ранг системи векторів, з яких вона складається. Хоча будь-яку матрицю можна уявити двома способами (вектори стовпці чи рядки), це впливає величину рангу, т.к.

1.14. зворотна матриця

Квадратна матриця A називається невиродженою, якщо вона має єдину зворотнуматрицю A -1 , що визначається умовами

AA −1 = A −1 A = I .

Зворотна матриця існує для всіх матриць. Необхідною та достатньою умовою невиродженості є

det(A ) ≠ 0 або rank(A ) = N.

Звернення матриці – це складна процедура, для виконання якої існують спеціальні програми. Наприклад,

Мал. 17 Звернення матриці

Наведемо формули для найпростішого випадку - матриці 2×2

Якщо матриці A і B невироджені, то

(AB) −1 = B −1 A −1 .

1.15. Псевдо зворотна матриця

Якщо матриця A вироджена та зворотна матриця не існує, то в деяких випадках можна використовувати псевдозворотнуматрицю, що визначається як така матриця A + , що

AA + A = A.

Псевдобрітельна матриця - не єдина і її вид залежить від способу побудови. Наприклад, для прямокутної матриці можна використовувати метод Мура-Пенроуза.

Якщо кількість стовпців менше числарядків, то

A + =(A t A ) −1 A t

Наприклад,

Мал. 17a Псевдообіг матриці

Якщо ж число стовпців більше числа рядків, то

A + =A t (AA t) −1

1.16. Розмноження вектора на матрицю

Вектор x можна множити на матрицю A відповідної розмірності. При цьому вектор-стовпець множиться праворуч Ax, а вектор рядок - зліва x t A. Якщо розмірність вектора J, а розмірність матриці I× Jто в результаті вийде вектор розмірності I. Наприклад,

Мал. 18 Розмноження вектора на матрицю

Якщо матриця A – квадратна ( I× I), вектор y = Ax має ту ж розмірність, що і x . Очевидно, що

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Тому матриці можна розглядати як лінійні перетвореннявекторів. Зокрема Ix = x, Ox = 0.

2. Додаткова інформація 2.1. Системи лінійних рівнянь

Нехай A – матриця розміром I× J, а b - вектор розмірності J. Розглянемо рівняння

Ax = b

щодо вектора x , розмірності I. По суті - це система з Iлінійних рівнянь з Jневідомими x 1 ,...,x J. Рішення існує в тому, і тільки в тому випадку, коли

rank(A ) = rank(B ) = R,

де B – це розширена матриця розмірності I×( J+1), що складається з матриці A, доповненої стовпцем b, B = (A b). Інакше рівняння несумісні.

Якщо R = I = J, то рішення єдине

x = A −1 b.

Якщо R < I, то існує безліч різних рішень, які можна виразити через лінійну комбінацію J−Rвекторів. Система однорідних рівнянь Ax = 0 із квадратною матрицею A ( N× N) має нетривіальне рішення (x ≠ 0 ) тоді і лише тоді, коли det(A ) = 0. Якщо R= Rank (A) 0.

Аналогічно визначаються негативно(x t Ax< 0), невід'ємно(x t Ax ≥ 0) та позитивно(x t Ax ≤ 0) певні матриці.

2.4. Розкладання Холецького

Якщо симетрична матриця A позитивно визначена, існує єдина трикутна матриця U з позитивними елементами, для якої

A = U t U.

Наприклад,

Мал. 19 Розкладання Холецького

2.5. Полярне розкладання

Нехай A – це невироджена квадратна матриця розмірності N× N. Тоді існує однозначне полярнеподання

A = SR,

де S – це невід'ємна симетрична матриця, а R – це ортогональна матриця. Матриці S і R можуть бути явно визначені:

S 2 = AA t або S = (AA t) ½ і R = S −1 A = (AA t) −½ A .

Наприклад,

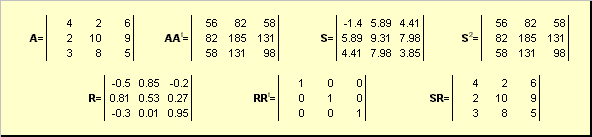
Мал. 20 Полярне розкладання

Якщо матриця A вироджена, то розкладання не єдине - а саме: S як і одна, а ось R може бути багато. Полярне розкладання представляє матрицю A як комбінацію стиснення/розтягування S та повороту R .

2.6. Власні вектори та власні значення

Нехай A – це квадратна матриця. Вектор v називається власним векторомматриці A якщо

Av = λv ,

де число λ називається власним значеннямматриці A. Таким чином, перетворення, яке виконує матриця A над вектором v , зводиться до простого розтягування або стиснення з коефіцієнтом λ. Власний вектор визначається з точністю до множення константу α ≠ 0, тобто. якщо v – власний вектор, то й αv – теж власний вектор.

2.7. Власні значення

У матриці A розмірністю ( N× N) не може бути більше ніж Nвласних значень. Вони задовольняють характеристичного рівняння

det(A − λI ) = 0,

що є алгебраїчним рівнянням N-го порядку. Зокрема, для матриці 2×2 характеристичне рівняння має вигляд

Наприклад,

Мал. 21 Власні значення

Набір власних значень λ 1 ,..., λ Nматриці A називається спектром A.

Спектр має різноманітні властивості. Зокрема

det(A ) = λ 1 ×...×λ N Sp(A) = λ 1 +...+λ N.

Власні значення довільної матриці можуть бути комплексними числами, проте якщо матриця симетрична (A t = A ), її власні значення речові.

2.8. Власні вектори

У матриці A розмірністю ( N× N) не може бути більше ніж Nвласних векторів, кожен із яких відповідає своєму власному значенню. Для визначення власного вектора v nпотрібно вирішити систему однорідних рівнянь

(A − λ n I) v n = 0 .

Вона має нетривіальне рішення, оскільки det(A − λ n I) = 0.

Наприклад,

Мал. 22 Власні вектори

Власні вектори симетричної матриці ортогональні.