2 чудовий. Калькулятор онлайн.Рішення меж

Формула другої чудової межі має вигляд lim x → ∞ 1 + 1 x x = e. Інша форма запису має такий вигляд: lim x → 0 (1 + x) 1 x = e .

Коли говоримо про другий чудовому межі, нам доводиться мати справу з невизначеністю виду 1 ∞ , тобто. одиницею нескінченною мірою.

Yandex.RTB R-A-339285-1

Розглянемо завдання, у яких нам знадобиться вміння обчислювати другий чудова межа.

Приклад 1

Знайдіть межу lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 .

Рішення

Підставимо потрібну формулу і виконаємо обчислення.

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞

У нас у відповіді вийшла одиниця в міру нескінченність. Щоб визначитися з методом розв'язання, використовуємо таблицю невизначеностей. Виберемо другу чудову межу і зробимо заміну змінних.

t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2

Якщо x → ∞ , то t → - ∞ .

Подивимося, що в нас вийшло після заміни:

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2

Відповідь: lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 .

Приклад 2

Обчисліть межу lim x → ∞ x - 1 x + 1 x.

Рішення

Підставимо нескінченність і отримаємо таке.

lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞

У відповіді у нас знову вийшло те саме, що й у попередньому завданні, отже, ми можемо знову скористатися другою чудовою межею. Далі нам потрібно виділити на підставі статечної функціїцілу частину:

x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1

Після цього межа набуває наступного вигляду:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x

Замінюємо змінні. Припустимо, що t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1; якщо x → ∞, то t → ∞.

Після цього записуємо, що в нас вийшло у вихідній межі:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t · 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t · lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 t t - 2 · 1 + 1 ∞ = e - 2 · (1 + 0) - 1 = e - 2

Щоб виконати це перетворення, ми використовували основні властивості меж і ступенів.

Відповідь: lim x → ∞ x - 1 x + 1 x = e-2.

Приклад 3

Обчисліть межу lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 .

Рішення

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞

Після цього нам потрібно виконати перетворення функції для застосування другої чудової межі. У нас вийшло таке:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

Оскільки зараз у нас є однакові показники ступеня в чисельнику і знаменнику дробу (рівні шести), то межа дробу на нескінченності дорівнюватиме відношенню даних коефіцієнтів при старших ступенях.

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3

При заміні t = x 2 + 2 x 2 – 1 – 2 x 2 + 2 у нас вийде друга чудова межа. Значить, що:

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3

Відповідь: lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e-3.

Висновки

Невизначеність 1 ∞, тобто. одиниця в нескінченній мірі, є статечною невизначеністю, отже, її можна розкрити, використовуючи правила знаходження меж показово статечних функцій.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

З вищевказаної статті Ви зможете дізнатися, що ж таке межа, і з чим її їдять – це дуже важливо. Чому? Можна не розуміти, що таке визначники та успішно їх вирішувати, можна зовсім не розуміти, що таке похідна та знаходити їх на «п'ятірку». Але якщо Ви не розумієте, що таке межа, то з вирішенням практичних завдань доведеться туго. Також не зайвим буде ознайомитись із зразками оформлення рішень та моїми рекомендаціями щодо оформлення. Вся інформація викладена у простій та доступній формі.

А для цілей цього уроку нам знадобляться такі методичні матеріали: Чудові межіі Тригонометричні формули. Їх можна знайти на сторінці. Найкраще методички роздрукувати - це значно зручніше, до того ж до них часто доведеться звертатися в офлайні.

Чим чудові межі? Чудовість цих меж полягає в тому, що вони доведені найбільшими розумами знаменитих математиків, і вдячним нащадкам не доводиться мучитися страшними межами з нагромадженням. тригонометричних функцій, логарифмів, ступенів. Тобто при знаходженні меж ми користуватимемося готовими результатами, які доведені теоретично.

Чудових меж існує кілька, але на практиці у студентів-заочників у 95% випадків фігурують дві чудові межі: Перша чудова межа, Друга чудова межа. Слід зазначити, що це назви, що історично склалися, і, коли, наприклад, говорять про «першу чудову межу», то мають на увазі під цим цілком певну річ, а не якусь випадкову, взяту зі стелі межу.

Перша чудова межа

Розглянемо наступна межа: (замість рідної літери «хе» я використовуватиму грецьку літеру «альфа», це зручніше з погляду подачі матеріалу).

Згідно з нашим правилом знаходження меж (див. статтю Межі. Приклади рішень) Пробуємо підставити нуль у функцію: в чисельнику у нас виходить нуль (синус нуля дорівнює нулю), у знаменнику, очевидно, теж нуль. Таким чином, ми стикаємося з невизначеністю виду, яку, на щастя, не треба розкривати. В курсі математичного аналізу, доводиться, що:

Цей математичний факт зветься Першої чудової межі. Аналітичний доказ межі наводити не буду, а ось його геометричний зміст розглянемо на уроці про нескінченно малих функціях.

Нерідко в практичних завданнях функції можуть бути по-іншому, це нічого не змінює:

– та сама перша чудова межа.

Але самостійно переставляти чисельник та знаменник не можна! Якщо дана межа у вигляді , то і вирішувати його потрібно в такому вигляді, нічого не переставляючи.

На практиці як параметр може виступати не тільки змінна, але і елементарна функція, складна функція. Важливо лише, щоб вона прагнула нуля.

Приклади:
, , ,

Тут , , , , і все гуд - перша чудова межа застосовується.

А ось наступний запис – єресь:

Чому? Тому що багаточлен не прагне нуля, він прагне п'ятірки.

До речі, питання на засипку, а чому дорівнює межа ? Відповідь можна знайти наприкінці уроку.

На практиці не все так гладко, майже ніколи студенту не запропонують вирішити халявну межу та отримати легкий залік. Хммм… Пишу ці рядки, і спала на думку дуже важлива думка – все-таки «халявні» математичні визначення та формули начебто краще пам'ятати напам'ять, це може надати неоціненну допомогу на заліку, коли питання вирішуватиметься між «двійкою» та «трійкою», і викладач вирішить поставити студенту якесь просте питання або запропонувати вирішити найпростіший приклад («а може він(а) все-таки знає чого?!»).

Переходимо до розгляду практичних прикладів:

Приклад 1

Знайти межу

Якщо ми помічаємо в межі синус, то це нас відразу має наштовхувати на думку про можливість застосування першої чудової межі.

Спочатку пробуємо підставити 0 у вираз під знак межі (робимо це подумки або на чернетці):

Отже, у нас є невизначеність виду, її обов'язково вказуємов оформленні рішення. Вираз під знаком межі у нас схоже на першу чудову межу, але це не зовсім він, під синусом знаходиться , а в знаменнику.

У подібних випадках перша чудова межа нам потрібно організувати самостійно, використовуючи штучний прийом. Хід міркувань може бути таким: "під синусом у нас, значить, у знаменнику нам теж потрібно отримати".
А робиться це дуже просто:

Тобто знаменник штучно множиться в даному випадкуна 7 і ділиться на ту ж сімку. Тепер запис у нас набув знайомих обрисів.
Коли завдання оформляється від руки, то перша чудова межа бажано помітити простим олівцем:

Що сталося? По суті, обведений вираз у нас перетворився на одиницю і зник у творі:

Тепер тільки залишилося позбутися триповерховості дробу:

Хто забув спрощення багатоповерхових дробів, будь ласка, освіжіть матеріал у довіднику Гарячі формули шкільного курсу математики .

Готово. Остаточна відповідь:

Якщо не хочеться використовувати позначки олівцем, то рішення можна оформити так:

“

Використовуємо першу чудову межу

“

Приклад 2

Знайти межу

Знову ми бачимо межі дріб і синус. Пробуємо підставити в чисельник і знаменник нуль:

Справді, у нас невизначеність і, отже, треба спробувати організувати першу чудову межу. На уроці Межі. Приклади рішеньми розглядали правило, що коли у нас є невизначеність, то потрібно розкласти чисельник та знаменник на множники. Тут – те саме, ступеня ми представимо як твори (множників):

Аналогічно попередньому прикладу, обводимо олівцем чудові межі (тут їх дві), і вказуємо, що вони прагнуть одиниці:

Власне, відповідь готова:

У наступних прикладах, я не займатимуся мистецтвами в Пейнті, думаю, як правильно оформляти рішення у зошиті – Вам вже зрозуміло.

Приклад 3

Знайти межу

Підставляємо нуль у вираз під знаком межі:

Отримано невизначеність, яку потрібно розкривати. Якщо в межі є тангенс, то майже завжди його перетворюють на синус і косинус за відомою тригонометричною формулою (до речі, з котангенсом роблять приблизно те саме, див. методичний матеріал Гарячі тригонометричні формулина сторінці Математичні формули, таблиці та довідкові матеріали).

В даному випадку:

Косинус нуля дорівнює одиниці, і його легко позбутися (не забуваємо помітити, що він прагне одиниці):

Отже, якщо межі косинус є МНОЖИТЕЛЕМ, його, грубо кажучи, треба перетворити на одиницю, що зникає у творі.

Тут все вийшло простіше, без жодних помножень і поділів. Перша чудова межа теж перетворюється на одиницю і зникає у творі:

У результаті отримано нескінченність, буває таке.

Приклад 4

Знайти межу

Пробуємо підставити нуль у чисельник та знаменник:

Отримана невизначеність (косинус нуля, як ми пам'ятаємо, дорівнює одиниці)

Використовуємо тригонометричну формулу. Візьміть на замітку! Межі із застосуванням цієї формули чомусь зустрічаються дуже часто.

Постійні множники винесемо за значок межі:

Організуємо першу чудову межу:

Тут у нас тільки одна чудова межа, яка перетворюється на одиницю і зникає у творі:

Позбавимося триповерховості:

Межа фактично вирішена, вказуємо, що синус, що залишився, прагне до нуля:

Приклад 5

Знайти межу

Цей приклад складніший, спробуйте розібратися самостійно:

Деякі межі можна звести до 1-ї чудової межі шляхом заміни змінної, про це можна прочитати трохи пізніше в статті Методи розв'язання меж.

Друга чудова межа

Теоретично математичного аналізу доведено, що:

Цей факт має назву другої чудової межі.

Довідка: - Це ірраціональне число.

Як параметр може бути як змінна , а й складна функція. Важливо лише, щоб вона прагнула нескінченності.

Приклад 6

Знайти межу

Коли вираз під знаком межі перебуває у ступені – це перша ознака того, що потрібно спробувати застосувати другу чудову межу.

Але спочатку, як завжди, пробуємо підставити нескінченно велике числоу вираз , за яким принципом це робиться, розібрано на уроці Межі. Приклади рішень.

Неважко помітити, що за основа ступеня , а показник – , тобто є, невизначеність виду:

Ця невизначеність якраз і розкривається за допомогою другої чудової межі. Але, як часто буває, друга чудова межа не лежить на блюдечку з блакитною облямівкою, і його потрібно штучно організувати. Розмірковувати можна так: даному прикладіПараметр, отже, у показнику нам теж потрібно організувати. Для цього зводимо основу в ступінь , і щоб вираз не змінилося - зводимо в ступінь :

Коли завдання оформляється від руки, позначаємо олівцем:

Практично все готово, страшний ступінь перетворився на симпатичну букву:

При цьому сам значок межі переміщуємо до показника:

Приклад 7

Знайти межу

Увага! Межа подібного типу зустрічається дуже часто, будь ласка, дуже уважно вивчіть цей приклад.

Пробуємо підставити нескінченно велике число у вираз, що стоїть під знаком межі:

В результаті отримано невизначеність. Але друга чудова межа застосовується до невизначеності виду. Що робити? Потрібно перетворити основу ступеня. Розмірковуємо так: у знаменнику у нас, значить, у чисельнику теж треба організувати.

У цій темі ми розберемо ті формули, які можна отримати, використовуючи другу чудову межу (тема, присвячена безпосередньо другій чудовій межі, знаходиться ). Нагадаю дві формулювання другої чудової межі, які знадобляться в цьому розділі: $\lim_(x\to\infty)\left(1+\frac(1)(x)\right)^x=e$ і $\lim_(x \to\ 0)\left(1+x\right)^\frac(1)(x)=e$.

Зазвичай формули я наводжу без доказів, але для цієї сторінки, гадаю, зроблю виняток. Справа в тому, що доказ наслідків з другої чудової межі містить деякі прийоми, які бувають корисними при безпосередньому вирішенні завдань. Ну, і взагалі кажучи, бажано знати, як доводиться та чи інша формула. Це дозволяє краще розуміти її внутрішню структуру, а також межі застосування. Але оскільки докази можуть бути цікаві не всім читачам, то приховую їх під примітки, які після кожного слідства.

Наслідок №1

\begin(equation) \lim_(x\to\ 0) \frac(\ln(1+x))(x)=1\end(equation)

Доказ слідства №1: показати/сховати

Так як при $ x \ to 0 $ маємо $ \ ln (1 + x) \ to 0 $, то в межах, що розглядається, є невизначеність виду $ \ frac (0) (0) $. Для розкриття цієї невизначеності представимо вираз $\frac(\ln(1+x))(x)$ у такому вигляді: $\frac(1)(x)\cdot\ln(1+x)$. Тепер внесемо множник $\frac(1)(x)$ у ступінь виразу $(1+x)$ і застосуємо другу чудову межу:

$$ \lim_(x\to\ 0) \frac(\ln(1+x))(x)=\left| \frac(0)(0) \right|= \lim_(x\to\ 0) \left(\frac(1)(x)\cdot\ln(1+x)\right)=\lim_(x\ to\ 0)\ln(1+x)^(\frac(1)(x))=\ln e=1. $$

Знову маємо невизначеність виду $ frac (0) (0) $. Будемо спиратися на вже доведену нами формулу. Так як $ log_a t = frac (l t) (l a) $, то $ log_a (1 + x) = frac (l (1 + x)) (l a) $.

$$ \lim_(x\to\ 0) \frac(\log_a (1+x))(x)=\left| \frac(0)(0) \right|=\lim_(x\to\ 0)\frac(\ln(1+x))( x \ln a)=\frac(1)(\ln a)\ lim_(x\to\ 0)\frac(\ln(1+x))( x)=\frac(1)(\ln a)\cdot 1=\frac(1)(\ln a). $$

Слідство №2

\begin(equation) \lim_(x\to\ 0) \frac(e^x-1)(x)=1\end(equation)

Доказ слідства №2: показати/сховати

Оскільки при $x\to 0$ маємо $e^x-1\to 0$, то розглянутому межі є невизначеність виду $\frac(0)(0)$. Для розкриття цієї невизначеності здійснимо заміну змінної, позначивши $t=e^x-1$. Оскільки $x\to 0$, то $t\to 0$. Далі, з формули $t=e^x-1$ отримаємо: $e^x=1+t$, $x=\ln(1+t)$.

$$ \lim_(x\to\ 0) \frac(e^x-1)(x)=\left| \frac(0)(0) \right|=\left | \begin(aligned) & t=e^x-1;\; t\to 0. \\ x =\ln(1+t).\end (aligned) \right|= \lim_(t\to 0)\frac(t)(\ln(1+t))= \lim_(t\to 0)\frac(1)(\frac(\ln(1+t))(t))=\frac(1)(1)=1. $$

Знову маємо невизначеність виду $ frac (0) (0) $. Будемо спиратися на вже доведену нами формулу. Оскільки $a^x=e^(x\ln a)$, то:

$$ \lim_(x\to\ 0) \frac(a^(x)-1)(x)=\left| \frac(0)(0) \right|=\lim_(x\to 0)\frac(e^(x\ln a)-1)(x)=\ln a\cdot \lim_(x\to 0 )\frac(e^(x\ln a)-1)(x \ln a)=\ln a \cdot 1=\ln a. $$

Слідство №3

\begin(equation) \lim_(x\to\ 0) \frac((1+x)^\alpha-1)(x)=\alpha \end(equation)

Доказ слідства №3: ​​показати/сховати

Знову маємо справу з невизначеністю виду $\frac(0)(0)$. Оскільки $(1+x)^\alpha=e^(\alpha\ln(1+x))$, то отримаємо:

$$ \lim_(x\to\ 0) \frac((1+x)^\alpha-1)(x)= \left| \frac(0)(0) \right|= \lim_(x\to\ 0)\frac(e^(\alpha\ln(1+x))-1)(x)= \lim_(x\to \ 0)\left(\frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x))\cdot \frac(\alpha\ln(1+x) )(x) \right)=\\ =\alpha\lim_(x\to\ 0) \frac(e^(\alpha\ln(1+x))-1)(\alpha\ln(1+x ))\cdot \lim_(x\to\ 0)\frac(\ln(1+x))(x)=\alpha\cdot 1\cdot 1=\alpha. $$

Приклад №1

Обчислити межу $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)$.

Маємо невизначеність виду $ frac (0) (0) $. Для розкриття цієї невизначеності використовуватимемо формулу . Щоб підігнати нашу межу під цю формулуслід пам'ятати, що вирази у ступеня числа $e$ й у знаменнику мають збігатися. Іншими словами, синусу у знаменнику не місце. У знаменнику має бути $9x$. Крім того, при вирішенні цього прикладу буде використано першу чудову межу .

$$ \lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\left|\frac(0)(0) \right|=\lim_(x\to\) 0) \left(\frac(e^(9x)-1)(9x)\cdot\frac(9x)(\sin 5x) \right) =\frac(9)(5)\cdot\lim_(x\ to\ 0) \left(\frac(e^(9x)-1)(9x)\cdot\frac(1)(\frac(\sin 5x)(5x)) \right)=\frac(9)( 5) cdot 1 cdot 1 = frac (9) (5). $$

Відповідь: $\lim_(x\to\ 0) \frac(e^(9x)-1)(\sin 5x)=\frac(9)(5)$.

Приклад №2

Обчислити межу $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)$.

Маємо невизначеність виду $ frac (0) (0) $ (нагадаю, що $ ln cos 0 = ln 1 = 0 $). Для розкриття цієї невизначеності використовуватимемо формулу . Спочатку врахуємо, що $\cos x=1-2\sin^2 \frac(x)(2)$ (див. роздрук за тригонометричними функціями). Тепер $\ln\cos x=\ln\left(1-2\sin^2 \frac(x)(2)\right)$, тому в знаменнику слід отримати вираз $-2\sin^2 \frac(x )(2)$ (щоб підігнати наш приклад під формулу). У подальшому рішенні буде використано першу чудову межу.

$$ \lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=\left| \frac(0)(0) \right|=\lim_(x\to\ 0) \frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(x ^2)= \lim_(x\to\ 0) \left(\frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(-2\sin^2 \frac(x)(2))\cdot\frac(-2\sin^2 \frac(x)(2))(x^2) \right)=\\ =-\frac(1)(2) \lim_(x\to\ 0) \left(\frac(\ln\left(1-2\sin^2 \frac(x)(2)\right))(-2\sin^2 \frac(x) )(2))\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)(2))\right)^2 \right)=-\frac(1)( 2) cdot 1 cdot 1^2=-frac(1)(2). $$

Відповідь: $\lim_(x\to\ 0) \frac(\ln\cos x)(x^2)=-\frac(1)(2)$.

Чудових меж існує кілька, але найвідомішими є перший і другий чудові межі. Чудовість цих меж полягає в тому, що вони мають широке застосуванняі з їхньою допомогою можна знайти й інші межі, що зустрічаються в численних завданнях. Цим ми і займатимемося в практичній частині цього уроку. Для вирішення завдань шляхом приведення до першої або другої чудової межі не потрібно розкривати невизначеності, що містяться в них, оскільки значення цих меж вже давно вивели великі математики.

Першою чудовою межеюназивається межа відношення синуса нескінченно малої дуги до тієї ж дуги, вираженої в радіанній мірі:

Переходимо до вирішення завдань на першу чудову межу. Зауважимо: якщо під знаком межі знаходиться тригонометрична функція, це майже вірна ознака того, що цей вираз можна привести до першої чудової межі.

приклад 1.Знайти межу.

Рішення. Підстановка замість xнуля призводить до невизначеності:

.

У знаменнику - синус, отже, вираз можна призвести до першої чудової межі. Починаємо перетворення:

.

У знаменнику - синус трьох ікс, а в чисельнику лише один ікс, отже, потрібно отримати три ікс і в чисельнику. Для чого? Щоб уявити 3 x = aі отримати вираз.

І приходимо до різновиду першої чудової межі:

тому що не має значення, яка літера (змінна) у цій формулі стоїть замість ікса.

Помножуємо ікс на три і відразу ділимо:

.

Відповідно до поміченої першої чудової межі робимо заміну дробового виразу:

Тепер можемо остаточно вирішити цю межу:

.

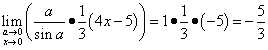приклад 2.Знайти межу.

Рішення. Безпосередня підстановка знову призводить до невизначеності "нуль ділити на нуль":

.

Щоб отримати першу чудову межу, потрібно, щоб ікс під знаком синуса в чисельнику і просто ікс у знаменнику були з тим самим коефіцієнтом. Нехай цей коефіцієнт дорівнюватиме 2. Для цього представимо нинішній коефіцієнт при іксі як і далі, роблячи дії з дробами, отримуємо:

.

приклад 3.Знайти межу.

Рішення. При підстановці знову отримуємо невизначеність "нуль ділити на нуль":

.

Напевно, вам уже зрозуміло, що з вихідного виразу можна отримати першу чудову межу, помножену на першу чудову межу. Для цього розкладаємо квадрати ікса в чисельнику і синуса в знаменнику на однакові множники, а щоб отримати у іксів і синуса однакові коефіцієнти, ікси в чисельникі ділимо на 3 і відразу множимо на 3. Отримуємо:

.

приклад 4.Знайти межу.

Рішення. Знову отримуємо невизначеність "нуль ділити на нуль":

.

Можемо отримати відношення двох перших чудових меж. Ділимо і чисельник, і знаменник на ікс. Потім, щоб коефіцієнти при синусах і при іксах збігалися, верхній ікс множимо на 2 і відразу ділимо на 2, а нижній ікс множимо на 3 і відразу ділимо на 3. Отримуємо:

Приклад 5.Знайти межу.

Рішення. І знову невизначеність "нуль ділити на нуль":

Пам'ятаємо з тригонометрії, що тангенс - це ставлення синуса до косінус, а косинус нуля дорівнює одиниці. Виробляємо перетворення та отримуємо:

.

Приклад 6.Знайти межу.

Рішення. Тригонометрична функція під знаком межі знову наштовхує на думку про застосування першої чудової межі. Представляємо його як ставлення синуса до косінус.

Знайти чудові межіважко не лише багатьом студентам першого, другого курсу навчання, які вивчають теорію меж, а й деяким викладачам.

Формула першої чудової межі

Наслідки першої чудової межі запишемо формулами
1. 2. 3. 4. Але власними силами загальні формулиЧудові межі нікому на іспиті або тесті не допомагають. Суть у тому, що реальні завдання побудовані так що до вищезаписаних формул потрібно ще прийти. І більшість студентів, які пропускають пари, заочно вивчають цей курс або мають викладачів, які самі не завжди розуміють, про що пояснюють, не можуть вирахувати самих елементарних прикладівна чудові межі. З формул першої чудової межі бачимо, що з їхньою допомогою можна дослідити невизначеності типу нуль розділити на нуль для виразів із тригонометричними функціями. Розглянемо спочатку ряд прикладів на першу чудову межу, а потім вивчимо другу чудову межу.

Приклад 1. Знайти межу функції sin(7*x)/(5*x)
Рішення: Як бачите функція під межею близька до першої чудової межі, але сама межа функції точно не дорівнює одиниці. У таких завданнях на межі слід у знаменнику виділити змінну з таким самим коефіцієнтом, який міститься при змінній під синусом. У цьому випадку слід розділити та помножити на 7

Деяким така деталізація здасться зайвою, але більшості студентів, яким важко даються межі, допоможе краще зрозуміти правила і засвоїти. теоретичний матеріал.
Також, якщо є зворотний виглядфункції - це також перша чудова межа. А все тому, що чудова межа дорівнює одиниці

Це правило стосується і наслідків 1 чудової межі. Тому якщо Вас запитають "Чому дорівнює перша чудова межа?" Ви без вагань повинні відповісти, що це одиниця.

Приклад 2. Знайти межу функції sin(6x)/tan(11x)
Рішення: Для розуміння кінцевого результату розпишемо функцію у вигляді

Щоб застосувати правила чудової межі помножимо та розділимо на множники

Далі межу добутку функцій розпишемо через добуток меж

Без складних формулми знайшли межу годинника тригонометричних функцій. Для засвоєння простих формул спробуйте придумати та знайти межу на 2 та 4 формулу слідства 1 чудової межі. Ми розглянемо складніші завдання.

Приклад 3. Обчислити межу (1-cos(x))/x^2
Рішення: Під час перевірки підстановкою отримаємо невизначеність 0/0 . Багатьом невідомо, як звести такий приклад до 1 чудової межі. Тут слід використовувати тригонометричну формулу

При цьому межа перетвориться на зрозумілий вигляд

Нам удалося звести функцію до квадрата чудової межі.

Приклад 4. Знайти межу
Рішення: При підстановці отримаємо знайому особливість 0/0. Однак змінна прагне Pi, а не нуля. Тому для застосування першої чудової межі виконаємо таку заміну змінної х, щоб нова змінна прямувала до нуля. Для цього знаменник позначимо за нову змінну Pi-x=y

Таким чином, використавши тригонометричну формулу, яка наведена в попередньому завданні, приклад зведений до 1 чудової межі.

Приклад 5. Обчислити межу
Рішення: Спочатку неясно, як спростити межі. Але якщо є приклад, то має бути і відповідь. Те, що змінна прямує до одиниці, дає при підстановці особливість виду нуль помножити на нескінченність, тому тангенс потрібно замінити за формулою.

Після цього отримаємо необхідність 0/0. Далі виконуємо заміну змінних у межі, і використовуємо періодичність котангенсу

Останні заміни дозволяють використовувати наслідок 1 чудової межі.

Друга чудова межа дорівнює експоненту

Це класика до якої реальних завданнях межі який завжди легко прийти.
У обчисленнях Вам знадобляться межі - наслідки другої чудової межі:
1. 2. 3. 4.
Завдяки другій чудовій межі та її наслідків можна дослідити невизначеності типу нуль розділити на нуль, одиниця в ступеня нескінченність, і нескінченність розділити на нескінченність, та ще й у такому ж ступені

Почнемо для ознайомлення з простих прикладів.

Приклад 6. Знайти межу функції
Рішення: Безпосередньо застосувати 2 чудові межі не вийде. Спочатку слід перетворити показник, щоб він мав вигляд зворотний до доданку в дужках

Це і є техніка зведення до 2 чудової межі та по суті - виведення 2 формули слідства межі.

Приклад 7. Знайти межу функції
Рішення: Маємо завдання на 3 формулу слідства 2 чудової межі. Підстановка нуля дає особливість 0/0. Для зведення межі під правило перетворимо знаменник, щоб при змінній був той самий коефіцієнт що і на логарифм

Це також легко зрозуміти та виконати на іспиті. Труднощі у студентів при обчисленні меж починаються з наступних завдань.

Приклад 8. Обчислити межу функції[(x+7)/(x-3)]^(x-2)
Рішення: Маємо особливість типу 1 ступеня нескінченність. Якщо не вірите, можете скрізь замість "ікс" підставити нескінченність і переконатись у цьому. Для зведення під правило поділимо в дужках чисельник на знаменник, для цього заздалегідь виконаємо маніпуляції

Підставимо вираз у межу і перетворимо до 2 чудової межі

Межа дорівнює експоненті 10 ступеня. Константи, які є доданками при змінній як у дужках так і ступеня ніякої "погоди" не вносять - слід пам'ятати. А якщо Вас спитають викладачі - "Чому не перетворюєте показник?" (Для цього прикладу в x-3), то скажіть що "Коли змінна прагне до нескінченності то до неї хоч додай 100 хоч забирай 1000, а межа залишиться такою як і був!".
Існує і другий спосіб обчислювати межі такого типу. Про нього розповімо у наступному завданні.

Приклад 9. Знайти межу
Рішення: Тепер винесемо змінну в чисельнику і знаменнику і перетворимо особливість на іншу. Для отримання кінцевого значення використовуємо формулу слідства 2 чудової межі

приклад 10. Знайти межу функції
Рішення: Задана межа знайти під силу не кожному. Для зведення під 2 межу уявімо, що sin (3x) це змінна, а потрібно перетворити показник

Далі показник запишемо як ступінь ступеня


У дужках описані проміжні міркування. В результаті використання першої та другої чудової межі отримали експоненту в кубі.

Приклад 11. Обчислити межу функції sin(2*x)/ln(3*x+1)
Рішення: Маємо невизначеність 0/0. Крім цього бачимо, що функцію слід перетворювати на використання обох чудових меж. Виконаємо попередні математичні перетворення

Далі легко межа прийме значення

Ось так вільно Ви почуватиметеся на контрольних роботах, тестах, модулях, якщо навчитеся швидко розписувати функції і зводити під першу чи другу чудову межу. Якщо завчити наведені методики знаходження меж Вам важко, завжди можете замовити контрольну роботуна межі у нас.
Для цього заповніть форму, вкажіть дані та вкладіть файл із прикладами. Ми допомогли багатьом студентам – зможемо допомогти і Вам!