සම්මත අපගමනය ඉක්මවා නැත. මධ්යන්ය රේඛීය සහ සම්මත අපගමනය
සම්මත අපගමනය ඉන් එකකි සංඛ්යානමය නියමයන්සංස්ථාපිත ලෝකයේ, සංවාදයක් හෝ ඉදිරිපත් කිරීමක් අතරතුර එය සාර්ථකව අවුල් කිරීමට සමත් වූ පුද්ගලයින්ගේ අධිකාරිය ඉහළ නැංවීමට ඔබට ඉඩ සලසයි, සහ එය කුමක්දැයි නොදන්නා නමුත් විමසීමට පසුබට වන අයට නොපැහැදිලි වැරදි වැටහීමක් ඇති කරයි. ඇත්ත වශයෙන්ම, බොහෝ කළමනාකරුවන් සම්මත අපගමනය පිළිබඳ සංකල්පය තේරුම් නොගන්නා අතර, ඔබ ඔවුන්ගෙන් කෙනෙකු නම්, ඔබ බොරුවෙන් ජීවත් වීම නැවැත්වීමට කාලයයි. අද ලිපියෙන්, මම ඔබට පෙන්වන්නේ මෙම අවතක්සේරු කළ සංඛ්යාලේඛන ඔබට ඔබ වැඩ කරන දත්ත වඩා හොඳින් තේරුම් ගැනීමට උපකාර වන ආකාරයයි.
සම්මත අපගමනය මනිනු ලබන්නේ කුමක්ද?
ඔබ සාප්පු දෙකක හිමිකරු බව සිතන්න. පාඩු වළක්වා ගැනීම සඳහා, කොටස් ශේෂය පිළිබඳ පැහැදිලි පාලනයක් තිබීම වැදගත්ය. හොඳම කොටස් කළමණාකරු කවුදැයි සොයා ගැනීමට උත්සාහ කිරීමේදී, ඔබ පසුගිය සති හය තුළ කොටස් විශ්ලේෂණය කිරීමට තීරණය කරයි. ගබඩා දෙකෙහිම තොගයේ සාමාන්ය සතිපතා පිරිවැය ආසන්න වශයෙන් සමාන වන අතර එය සාම්ප්රදායික ඒකක 32ක් පමණ වේ. මුලින්ම බැලූ බැල්මට, කොටස්වල සාමාන්ය අගය පෙන්නුම් කරන්නේ කළමනාකරුවන් දෙදෙනාම එකම ආකාරයකින් ක්රියා කරන බවයි.

නමුත් ඔබ දෙවන ගබඩාවේ ක්රියාකාරිත්වය දෙස සමීපව බැලුවහොත්, සාමාන්ය අගය නිවැරදි වුවද, කොටස් විචල්යතාවය ඉතා ඉහළ මට්ටමක පවතින බව ඔබට පෙනේ (10 සිට 58 USD දක්වා). මේ අනුව, මධ්යන්යය සෑම විටම දත්ත නිවැරදිව තක්සේරු නොකරන බව නිගමනය කළ හැකිය. මෙන්න එය ප්රයෝජනවත් වේ සම්මත අපගමනය.
සම්මත අපගමනය පෙන්නුම් කරන්නේ අගයන් අපගේ අගයට සාපේක්ෂව බෙදා හරින ආකාරයයි. වෙනත් වචන වලින් කිවහොත්, සතියෙන් සතියට ගලා යාම කොතරම් විශාලද යන්න ඔබට තේරුම් ගත හැකිය.
අපගේ උදාහරණයේ දී, අපි භාවිතා කර ඇත එක්සෙල් කාර්යයමධ්යන්යය සමඟ සම්මත අපගමන ලකුණු ගණනය කිරීමට STDEV.

පළමු කළමනාකරු සම්බන්ධයෙන් ගත් කල, සම්මත අපගමනය 2 විය. මෙයින් අපට පවසන්නේ නියැදියේ එක් එක් අගය සාමාන්යයෙන් මධ්යන්යයෙන් 2 කින් අපගමනය වන බවයි. ඒක හොඳයි? අපි ප්රශ්නය වෙනත් කෝණයකින් බලමු - 0 හි සම්මත අපගමනය අපට පවසන්නේ නියැදියේ එක් එක් අගය එහි මධ්යන්ය අගයට සමාන වන බවයි (අපගේ නඩුවේදී, 32.2). උදාහරණයක් ලෙස, 2 හි සම්මත අපගමනය 0 ට වඩා බොහෝ වෙනස් නොවේ, බොහෝ අගයන් මධ්යන්යයට ආසන්න බව පෙන්නුම් කරයි. සම්මත අපගමනය 0 ට ආසන්න වන තරමට මධ්යන්යය වඩාත් විශ්වාසදායක වේ. තවද, 0 ට ආසන්න සම්මත අපගමනය දත්තවල සුළු විචල්යතාවයක් පෙන්නුම් කරයි. එනම්, 2 හි සම්මත අපගමනය සහිත සින්ක් අගයක් පළමු කළමනාකරුගේ ඇදහිය නොහැකි අනුකූලතාව පෙන්නුම් කරයි.
දෙවන ගබඩාව සම්බන්ධයෙන්, සම්මත අපගමනය 18.9 කි. එනම්, ගලා යාමේ පිරිවැය සතියෙන් සතියට සාමාන්ය අගයෙන් 18.9 කින් සාමාන්යයෙන් අපගමනය වේ. පිස්සු පැතිරෙනවා! තවදුරටත් සම්මත අපගමනය 0 සිට, මධ්යන්යය අඩු නිවැරදි වේ. අපගේ නඩුවේදී, 18.9 හි රූපය පෙන්නුම් කරන්නේ සාමාන්ය අගය (සතියකට ඩොලර් 32.8) සරලව විශ්වාස කළ නොහැකි බවයි. සතිපතා ගලායාම ඉතා විචල්ය වන බව ද එය අපට කියයි.
මෙය කෙටියෙන් සම්මත අපගමනය පිළිබඳ සංකල්පයයි. එය අනෙකුත් වැදගත් සංඛ්යාන මිනුම් (ප්රකාරය, මධ්යස්ථ...) පිළිබඳ අවබෝධයක් ලබා නොදෙන නමුත් ඇත්ත වශයෙන්ම සම්මත අපගමනය බොහෝ සංඛ්යානමය ගණනය කිරීම් වලදී තීරණාත්මක කාර්යභාරයක් ඉටු කරයි. සම්මත අපගමනය පිළිබඳ මූලධර්ම අවබෝධ කර ගැනීම ඔබේ ක්රියාකාරකම්වල බොහෝ ක්රියාවලීන්ගේ සාරය මත ආලෝකය විහිදුවයි.
සම්මත අපගමනය ගණනය කරන්නේ කෙසේද?
ඉතින්, දැන් අපි සම්මත අපගමනය රූපය පවසන දේ දන්නවා. අපි බලමු කොහොමද ගණන් ගන්නේ කියලා.
10 කින් වර්ධක 10 සිට 70 දක්වා දත්ත කට්ටලයක් සලකා බලන්න. ඔබට පෙනෙන පරිදි, මම දැනටමත් සෛල H2 (තැඹිලි) හි STDEV ශ්රිතය භාවිතයෙන් ඒවා සඳහා සම්මත අපගමනය ගණනය කර ඇත.

එක්සෙල් 21.6ට පැමිණීමට ගන්නා පියවර පහත දැක්වේ.
සියලු ගණනය කිරීම් වඩා හොඳ අවබෝධයක් සඳහා දෘශ්යමාන කර ඇති බව කරුණාවෙන් සලකන්න. ඇත්ත වශයෙන්ම, Excel හි, ගණනය කිරීම ක්ෂණිකව සිදු වන අතර, තිරය පිටුපස සියලු පියවර තබයි.
Excel මුලින්ම නියැදියේ මධ්යන්යය සොයා ගනී. අපගේ නඩුවේදී, සාමාන්යය 40 ක් බවට පත් වූ අතර එය ඊළඟ පියවරේදී එක් එක් නියැදි අගයෙන් අඩු කරනු ලැබේ. එක් එක් ප්රතිඵලය වන වෙනස වර්ග කර සාරාංශ කර ඇත. අපට 2800 ට සමාන එකතුවක් ලැබුණි, එය නියැදි මූලද්රව්ය සංඛ්යාවෙන් බෙදිය යුතු අතර එය 1 අඩු කළ යුතුය. අපට මූලද්රව්ය 7 ක් ඇති බැවින්, අපට 2800 න් 6 න් බෙදිය යුතු බව පෙනේ. ප්රතිඵලයෙන් අපට වර්ගමූලය, මෙම රූපය සොයා ගනී. සම්මත අපගමනය වනු ඇත.

දෘශ්යකරණය භාවිතයෙන් සම්මත අපගමනය ගණනය කිරීමේ මූලධර්මය මත සම්පූර්ණයෙන්ම පැහැදිලි නැති අය සඳහා, මම මෙම අගය සොයා ගැනීම සඳහා ගණිතමය අර්ථකථනයක් ලබා දෙමි.

Excel හි සම්මත අපගමනය ගණනය කිරීමේ කාර්යයන්
Excel හි සම්මත අපගමන සූත්ර වර්ග කිහිපයක් තිබේ. ඔබට අවශ්ය වන්නේ =STDEV ටයිප් කිරීම පමණක් වන අතර ඔබට එය පෙනෙනු ඇත.

STDEV.V සහ STDEV.G (ලැයිස්තුවේ පළමු සහ දෙවන ශ්රිත) ශ්රිතයන් කලින් සමග ගැළපීම සඳහා රඳවාගෙන සිටි STDEV සහ STDEV (ලැයිස්තුවේ පස්වන සහ හයවන ශ්රිත) ශ්රිත අනුපිටපත් කරන බව සඳහන් කිරීම වටී. Excel හි අනුවාද.
සාමාන්යයෙන්, .V සහ .G ශ්රිතවල අවසානයෙහි වෙනස පෙන්නුම් කරන්නේ නියැදි සම්මත අපගමනය ගණනය කිරීමේ මූලධර්මය හෝ ජනගහනය. මම කලින් එකේ මේ array දෙකේ වෙනස පැහැදිලි කරලා තියෙනවා.
STDEV සහ STDEVPA ශ්රිතවල ලක්ෂණයක් (ලැයිස්තුවේ තුන්වන සහ සිව්වන ශ්රිත) අරාවක සම්මත අපගමනය ගණනය කිරීමේදී තාර්කික සහ පෙළ අගයන් සැලකිල්ලට ගනී. පෙළ සහ සත්ය බූලියන 1 වන අතර ව්යාජ බූලියන 0. මෙම ශ්රිත දෙක මට අවශ්ය වේ යැයි මට සිතීම දුෂ්කර ය, එබැවින් ඒවා නොසලකා හැරිය හැකි යැයි මම සිතමි.
උපදෙස්
සංලක්ෂිත සංඛ්යා කිහිපයක් තිබිය යුතුය - හෝ සමජාතීය ප්රමාණ. උදාහරණයක් ලෙස, මිනුම්, කිරුම්, සංඛ්යාන නිරීක්ෂණ ආදියෙහි ප්රතිඵල. ඉදිරිපත් කරන ලද සියලුම ප්රමාණ එකම මිනුමකින් මැනිය යුතුය. සොයා ගැනීමට සම්මත අපගමනය, පහත දේ කරන්න.
සියලුම සංඛ්යා වල අංක ගණිත මධ්යන්යය නිර්ණය කරන්න: සියලුම සංඛ්යා එකතු කර එකතුව බෙදන්න සමස්තඅංක.
සංඛ්යාවල විසරණය (විසුරුම) නිර්ණය කරන්න: කලින් සොයාගත් අපගමනයන්හි වර්ග එකතු කර ලැබෙන එකතුව සංඛ්යා ගණනින් බෙදන්න.
සෙල්සියස් අංශක 34, 35, 36, 37, 38, 39 සහ 40 උෂ්ණත්වය සහිත වාට්ටුවේ රෝගීන් හත් දෙනෙක් සිටිති.
සාමාන්යයෙන් සිට සාමාන්ය අපගමනය තීරණය කිරීම අවශ්ය වේ.
විසඳුමක්:
"වාට්ටුවේ": (34+35+36+37+38+39+40)/7=37 ºС;
සාමාන්යයෙන් උෂ්ණත්ව අපගමනය (in මෙම නඩුවසාමාන්ය අගය): 34-37, 35-37, 36-37, 37-37, 38-37, 39-37, 40-37, එය හැරෙනවා: -3, -2, -1, 0, 1, 2 , 3 (ºС);
කලින් ලබාගත් සංඛ්යා එකතුව ඒවායේ අංකයෙන් බෙදන්න. ගණනය කිරීමේ නිරවද්යතාවය සඳහා, කැල්කියුලේටරය භාවිතා කිරීම වඩා හොඳය. බෙදීමේ ප්රතිඵලය සාරාංශවල අංක ගණිත මධ්යන්යය වේ.
අවම වශයෙන් එක් ගණනය කිරීමක දෝෂයක් වැරදි අවසාන දර්ශකයකට තුඩු දෙනු ඇති බැවින්, ගණනය කිරීමේ සියලුම අදියර කෙරෙහි අවධානය යොමු කරන්න. එක් එක් අදියරේදී ලැබුණු ගණනය කිරීම් පරීක්ෂා කරන්න. අංක ගණිත සාමාන්යයට සංඛ්යාවල එකතුවට සමාන මීටරයක් ඇත, එනම්, ඔබ සාමාන්ය පැමිණීම තීරණය කරන්නේ නම්, සියලුම දර්ශක “පුද්ගලයා” වනු ඇත.
මෙම ක්රමයගණනය කිරීම භාවිතා කරනුයේ ගණිතමය සහ සංඛ්යානමය ගණනය කිරීම් වලදී පමණි. උදාහරණයක් ලෙස, පරිගණක විද්යාවේ අංක ගණිත මධ්යන්යය වෙනස් ගණනය කිරීමේ ඇල්ගොරිතමයක් ඇත. අංක ගණිත මධ්යන්යය ඉතා කොන්දේසි සහිත දර්ශකයකි. එය සිදුවීමක සම්භාවිතාව පෙන්නුම් කරයි, එයට ඇත්තේ එක් සාධකයක් හෝ දර්ශකයක් පමණි. වඩාත් ගැඹුරු විශ්ලේෂණයක් සඳහා, බොහෝ සාධක සැලකිල්ලට ගත යුතුය. මේ සඳහා වඩාත් පොදු ප්රමාණ ගණනය කිරීම භාවිතා වේ.
ගණිතය සහ සංඛ්යානමය ගණනය කිරීම් වලදී බහුලව භාවිතා වන මධ්යම ප්රවණතාවයේ මිනුම් වලින් එකක් අංක ගණිත මධ්යන්යය වේ. අගයන් කිහිපයක ගණිතමය සාමාන්යය සොයා ගැනීම ඉතා සරල ය, නමුත් සෑම කාර්යයකටම තමන්ගේම සූක්ෂ්මතා ඇත, ඒවා නිවැරදි ගණනය කිරීම් සිදු කිරීම සඳහා දැන ගැනීම අවශ්ය වේ.
එවැනි අත්හදා බැලීම්වල ප්රමාණාත්මක ප්රතිඵල.
ගණිත මධ්යන්යය සොයා ගන්නේ කෙසේද
සාමාන්යයක් සොයා ගැනීම අංක ගණිත අංකයසංඛ්යා මාලාවක් සඳහා, ඔබ ආරම්භ කළ යුත්තේ මෙම අගයන්හි වීජීය එකතුව නිර්ණය කිරීමෙනි. උදාහරණයක් ලෙස, අරාවෙහි අංක 23, 43, 10, 74 සහ 34 අඩංගු වේ නම්, ඒවායේ වීජීය එකතුව 184 වනු ඇත. ලිවීමේදී අංක ගණිත මධ්යන්යය μ (mu) හෝ x (x තීරුවක් සහිත) අක්ෂරයෙන් දැක්වේ. . ඊළඟට වීජීය එකතුව අරාවේ ඇති සංඛ්යා ගණනින් බෙදිය යුතුය. මෙම උදාහරණයේ සංඛ්යා පහක් තිබූ බැවින් අංක ගණිත මධ්යන්යය 184/5 වන අතර 36.8 වනු ඇත.සෘණ සංඛ්යා සමඟ වැඩ කිරීමේ විශේෂාංග
අරාව අඩංගු නම් සෘණ සංඛ්යා, එවිට ගණිත මධ්යන්යය සොයා ගැනීම සමාන ඇල්ගොරිතමයකට අනුව සිදු වේ. වෙනසක් ඇත්තේ ක්රමලේඛන පරිසරය තුළ ගණනය කිරීමේදී හෝ කාර්යය තිබේ නම් පමණි අතිරේක කොන්දේසි. මෙම අවස්ථා වලදී, සමඟ සංඛ්යා වල අංක ගණිත මධ්යන්යය සොයා ගැනීම විවිධ සංඥාපියවර තුනක් දක්වා පහත වැටේ:1. සම්මත ක්රමය මගින් පොදු අංක ගණිත මධ්යන්යය සොයා ගැනීම;
2. සෘණ සංඛ්යා වල ගණිත මධ්යන්යය සොයා ගැනීම.
3. ධන සංඛ්යා වල අංක ගණිත මධ්යන්යය ගණනය කිරීම.
එක් එක් ක්රියාවන්හි ප්රතිචාර කොමාවෙන් වෙන්කර ලියා ඇත.
ස්වභාවික හා දශම භාගය
ඉලක්කම් මාලාවක් ඉදිරිපත් කරන්නේ නම් දශම, නිඛිලවල අංක ගණිත මධ්යන්යය ගණනය කිරීමේ ක්රමයට අනුව විසඳුම සිදු වේ, නමුත් පිළිතුරේ නිරවද්යතාවය සඳහා ගැටලුවේ අවශ්යතා අනුව ප්රති result ලය අඩු වේ.සමඟ වැඩ කරන විට ස්වභාවික කොටස්ඔවුන් වෙත ගෙන ආ යුතුය පොදු හරය, එය අරාවේ ඇති සංඛ්යා ගණනින් ගුණ කරනු ලැබේ. පිළිතුරේ සංඛ්යාංකය මුල් භාගික මූලද්රව්යවල දී ඇති සංඛ්යාවල එකතුව වනු ඇත.
මෙම ලිපියෙන් මම ඒ ගැන කතා කරමි සාමාන්යය සොයා ගන්නේ කෙසේද සම්මත අපගමනය . ගණිතය පිළිබඳ පූර්ණ අවබෝධයක් සඳහා මෙම ද්රව්යය අතිශයින්ම වැදගත් වේ, එබැවින් ගණිත උපදේශකයෙකු එය අධ්යයනය කිරීම සඳහා වෙනම පාඩමක් හෝ කිහිපයක් පවා කැප කළ යුතුය. මෙම ලිපියෙන්, සම්මත අපගමනය යනු කුමක්ද සහ එය සොයා ගන්නේ කෙසේද යන්න පැහැදිලි කරන සවිස්තරාත්මක සහ තේරුම්ගත හැකි වීඩියෝ නිබන්ධනයකට සබැඳියක් ඔබට සොයාගත හැකිය.
සම්මත අපගමනයයම් පරාමිතියක් මැනීමේ ප්රතිඵලයක් ලෙස ලබාගත් අගයන් පැතිරීම තක්සේරු කිරීමට හැකි වේ. එය සංකේතයක් (ග්රීක අකුර "සිග්මා") මගින් දැක්වේ.
ගණනය කිරීම සඳහා සූත්රය තරමක් සරල ය. සම්මත අපගමනය සොයා ගැනීමට, ඔබ විචලනයේ වර්ගමූලය ගත යුතුය. එබැවින් දැන් ඔබට අසන්නට ඇත්තේ "විචලනය යනු කුමක්ද?"
විසරණය යනු කුමක්ද
විචලනය පිළිබඳ අර්ථ දැක්වීම පහත පරිදි වේ. විසරණය යනු මධ්යන්යයෙන් අගයන්හි වර්ග අපගමනයන්හි අංක ගණිත මධ්යන්යය වේ.
විචලනය සොයා ගැනීමට, පහත ගණනය කිරීම් අනුපිළිවෙලින් සිදු කරන්න:
- මධ්යන්යය (අගය මාලාවක සරල ගණිත මධ්යන්ය) නිර්ණය කරන්න.
- ඉන්පසු එක් එක් අගයන්ගෙන් සාමාන්යය අඩු කර ලැබෙන වෙනස වර්ග කරන්න (අපට ලැබුණි වෙනස වර්ග).
- මීලඟ පියවර වන්නේ ලබාගත් වෙනස්කම්වල වර්ගවල අංක ගණිත මධ්යන්යය ගණනය කිරීමයි (ඔබට හරියටම වර්ග පහතින් ඇත්තේ මන්දැයි සොයා ගත හැක).
අපි උදාහරණයක් බලමු. ඔබ සහ ඔබේ මිතුරන් ඔබේ බල්ලන්ගේ උස (මිලිමීටර වලින්) මැනීමට තීරණය කළ බව කියමු. මිනුම්වල ප්රති result ලයක් ලෙස, ඔබට පහත උස මිනුම් (මැලවී යාමේදී) ලැබුණි: 600 mm, 470 mm, 170 mm, 430 mm සහ 300 mm.
මධ්යන්ය, විචලනය සහ සම්මත අපගමනය ගණනය කරමු.
අපි මුලින්ම සාමාන්යය සොයා ගනිමු. ඔබ දැනටමත් දන්නා පරිදි, මේ සඳහා ඔබ මනින ලද සියලුම අගයන් එකතු කර මිනුම් ගණනින් බෙදිය යුතුය. ගණනය කිරීමේ ප්රගතිය:
සාමාන්ය මි.මී.
ඉතින්, සාමාන්ය (අංක ගණිත මධ්යන්ය) 394 මි.මී.
දැන් අපි නිර්වචනය කළ යුතුයි එක් එක් සුනඛයාගේ උස සාමාන්යයෙන් බැහැර වීම:

අවසාන, විචලනය ගණනය කිරීමට, ලබාගත් එක් එක් වෙනස්කම් වර්ග කර ඇති අතර, පසුව ලබාගත් ප්රතිඵලවල අංක ගණිත මධ්යන්යය අපි සොයා ගනිමු:
විසරණය mm 2 .
මේ අනුව, විසුරුම 21704 mm 2 වේ.
සම්මත අපගමනය සොයා ගන්නේ කෙසේද
එසේනම් විචලනය දැනගෙන සම්මත අපගමනය ගණනය කරන්නේ කෙසේද? අපට මතක ඇති පරිදි, එහි වර්ග මූලය ගන්න. එනම්, සම්මත අපගමනය:
mm (මි.මී. වලින් ආසන්නතම සම්පූර්ණ සංඛ්යාවට වට කර ඇත).
මෙම ක්රමය භාවිතා කිරීමෙන්, සමහර සුනඛයන් (උදාහරණයක් ලෙස, Rottweilers) ඉතා හොඳ බව අපට පෙනී ගියේය විශාල බල්ලන්. නමුත් ඉතා කුඩා සුනඛයන් ද ඇත (උදාහරණයක් ලෙස, ඩච්ෂුන්ඩ්, නමුත් ඔබ මෙය ඔවුන්ට නොකිය යුතුය).
වඩාත්ම සිත්ගන්නා කරුණ නම් සම්මත අපගමනය දරයි ප්රයෝජනවත් තොරතුරු. දැන් අපට සාමාන්ය (එහි දෙපැත්තේම) සම්මත අපගමනයෙන් වෙන් කළහොත් අපට ලැබෙන පරතරය තුළ වර්ධනය මනින ලද ප්රතිඵල මොනවාදැයි පෙන්විය හැක.
එනම්, සම්මත අපගමනය භාවිතා කරමින්, අපට සාමාන්ය (සංඛ්යාන සාමාන්ය) සහ අසාමාන්ය ලෙස විශාල හෝ අනෙක් අතට කුඩා අගයන් මොනවාදැයි සොයා ගැනීමට ඔබට ඉඩ සලසන “සම්මත” ක්රමයක් ලැබේ.
සම්මත අපගමනය යනු කුමක්ද?
නමුත් ... අපි විශ්ලේෂණය කළහොත් දේවල් ටිකක් වෙනස් වනු ඇත නියැදීමදත්ත. අපගේ උදාහරණයේදී අපි සලකා බැලුවෙමු සාමාන්ය ජනතාව.එනම්, අපගේ සුනඛයන් 5 දෙනා අපට උනන්දුවක් දැක්වූ ලෝකයේ එකම සුනඛයන්ය.
නමුත් දත්ත නියැදියක් නම් (විශාල ජනගහනයකින් තෝරාගත් අගයන්), එවිට ගණනය කිරීම් වෙනස් ආකාරයකින් සිදු කළ යුතුය.
අගයන් තිබේ නම්, එසේ නම්:
සාමාන්යය තීරණය කිරීම ඇතුළුව අනෙකුත් සියලුම ගණනය කිරීම් එකම ආකාරයකින් සිදු කෙරේ.
නිදසුනක් වශයෙන්, අපගේ සුනඛයන් පස්දෙනා සුනඛ ගහනයක (පෘථිවියේ සිටින සියලුම සුනඛයන්) නියැදියක් පමණක් නම්, අප විසින් බෙදිය යුතුය 5 වෙනුවට 4එනම්:
නියැදි විචලනය = ![]() mm 2
mm 2
මෙම අවස්ථාවේදී, නියැදිය සඳහා සම්මත අපගමනය සමාන වේ ![]() මි.මී. (ළඟම සම්පූර්ණ අංකයට වටකුරු).
මි.මී. (ළඟම සම්පූර්ණ අංකයට වටකුරු).
අපගේ අගයන් කුඩා නියැදියක් වන විට අපි යම් "නිවැරදි කිරීමක්" කළ බව අපට පැවසිය හැකිය.
සටහන. වෙනස්කම්වල වර්ග හරියටම ඇයි?
නමුත් විචලනය ගණනය කිරීමේදී අපි වෙනස්කම්වල වර්ග ගන්නේ ඇයි? යම් පරාමිතියක් මැනීමේදී අපි පිළිගනිමු, ඔබට පහත අගයන් කට්ටලය ලැබී ඇත: 4; හතර; -හතර; -හතර. අපි එකිනෙකා අතර මධ්යන්ය (වෙනස) වලින් නිරපේක්ෂ අපගමනය එකතු කළහොත්... සෘණ අගයන්ධනාත්මක ඒවා සමඟ එකිනෙකා අවලංගු කරන්න:
![]() .
.
මෙම විකල්පය නිෂ්ඵල බව පෙනී යයි. එවිට අපගමනයන්හි නිරපේක්ෂ අගයන් (එනම්, මෙම අගයන්හි මොඩියුල) උත්සාහ කිරීම වටී ද?
මුලින්ම බැලූ බැල්මට එය නරක නොවන බව පෙනේ (ප්රතිඵලයක් ලෙස ලැබෙන අගය, මධ්යන්ය නිරපේක්ෂ අපගමනය ලෙස හැඳින්වේ), නමුත් සෑම අවස්ථාවකදීම නොවේ. අපි තවත් උදාහරණයක් උත්සාහ කරමු. මිනුම් ප්රතිඵලය පහත අගයන් සමූහයට ඉඩ දෙන්න: 7; එක; -6; -2. එවිට මධ්යන්ය නිරපේක්ෂ අපගමනය වන්නේ:
Blimey! වෙනස්කම් වඩා විශාල ව්යාප්තියක් තිබුණද, අපට නැවතත් ප්රතිඵලය 4 ලැබුණි.
දැන් අපි බලමු වෙනස්කම් වර්ග කළොත් (ඊට පස්සේ ඒවායේ එකතුවේ වර්ගමූලය ගන්න) මොකද වෙන්නේ කියලා.
පළමු උදාහරණය සඳහා, ඔබට ලැබෙන්නේ:
![]() .
.
දෙවන උදාහරණය සඳහා, ඔබට ලැබෙන්නේ:
දැන් එය සම්පූර්ණයෙන්ම වෙනස් කාරණයක්! මූල-මධ්යන්-චතුරස්ර අපගමනය වැඩි වන තරමට වෙනස්කම් පැතිරීම වැඩි වේ ... අප උත්සාහ කළේ එයයි.
ඇත්ත වශයෙන්ම, තුළ මෙම ක්රමයලකුණු අතර දුර ගණනය කිරීමේදී එම අදහසම භාවිතා වේ, වෙනත් ආකාරයකින් පමණක් යොදනු ලැබේ.
සහ ගණිතමය දෘෂ්ටි කෝණයකින්, වර්ග භාවිතය සහ වර්ග මුල්අපගමනයන්හි නිරපේක්ෂ අගයන්ගෙන් අපට ලබාගත හැකි අගයට වඩා වැඩි අගයක් ලබා දෙයි, එම නිසා සම්මත අපගමනය අනෙකුත් ගණිතමය ගැටළු සඳහා අදාළ වේ.
සම්මත අපගමනය සොයා ගන්නේ කෙසේදැයි සර්ජි Valerievich ඔබට කීවේය
$X$. පළමුව, පහත අර්ථ දැක්වීම සිහිපත් කරමු:
අර්ථ දැක්වීම 1
ජනගහන-- දී ඇති වර්ගයක අහඹු ලෙස තෝරාගත් වස්තු සමූහයක්, අහඹු විචල්යයක නිශ්චිත අගයන් ලබා ගැනීම සඳහා නිරීක්ෂණ සිදු කරනු ලබන අතර, දී ඇති වර්ගයක අහඹු විචල්යයක් අධ්යයනය කිරීමේදී නොවෙනස්ව පවතින තත්වයන් යටතේ සිදු කෙරේ.
අර්ථ දැක්වීම 2
සාමාන්ය විචලනය-- සාමාන්ය ජනගහනයේ ප්රභේදයේ අගයන් ඔවුන්ගේ මධ්යන්ය අගයෙන් වර්ග කළ අපගමනයන්හි අංක ගණිත මධ්යන්යය.
$x_1,\ x_2,\dots ,x_k$ යන විචල්යයේ අගයන් පිළිවෙලින් $n_1,\ n_2,\dots ,n_k$ සංඛ්යාත ඇති කිරීමට ඉඩ දෙන්න. එවිට සාමාන්ය විචලනය සූත්රය මගින් ගණනය කරනු ලැබේ:
සලකා බලන්න විශේෂ අවස්ථාවක්. සියලුම ප්රභේද $x_1,\ x_2,\dots ,x_k$ වෙනස් වීමට ඉඩ දෙන්න. මෙම අවස්ථාවේදී $n_1,\ n_2,\dots ,n_k=1$. මෙම අවස්ථාවේදී සාමාන්ය විචලනය සූත්රය මගින් ගණනය කරනු ලබන බව අපට ලැබේ:
මෙම සංකල්පයට සම්බන්ධ වන්නේ සාමාන්ය සම්මත අපගමනය යන සංකල්පයයි.
අර්ථ දැක්වීම 3
සාමාන්ය සම්මත අපගමනය
\[(\sigma )_r=\sqrt(D_r)\]
නියැදි විචලනය
$X$ සසම්භාවී විචල්යයක් සම්බන්ධයෙන් අපට නියැදි කට්ටලයක් ලබා දෙමු. පළමුව, පහත අර්ථ දැක්වීම සිහිපත් කරමු:
අර්ථ දැක්වීම 4
නියැදි ජනගහනය-- සාමාන්ය ජනගහනයෙන් තෝරාගත් වස්තූන්ගෙන් කොටසක්.
අර්ථ දැක්වීම 5
නියැදි විචලනය-- සාමාන්ය අංක ගණිත අගයන්නියැදි විකල්පය.
$x_1,\ x_2,\dots ,x_k$ යන විචල්යයේ අගයන් පිළිවෙලින් $n_1,\ n_2,\dots ,n_k$ සංඛ්යාත ඇති කිරීමට ඉඩ දෙන්න. එවිට නියැදි විචලනය සූත්රය මගින් ගණනය කරනු ලැබේ:
අපි විශේෂ අවස්ථාවක් සලකා බලමු. සියලුම ප්රභේද $x_1,\ x_2,\dots ,x_k$ වෙනස් වීමට ඉඩ දෙන්න. මෙම අවස්ථාවේදී $n_1,\ n_2,\dots ,n_k=1$. මෙම අවස්ථාවේදී, නියැදි විචලනය සූත්රය මගින් ගණනය කරනු ලබන බව අපට ලැබේ:
මෙම සංකල්පයට සම්බන්ධ වන්නේ නියැදි සම්මත අපගමනය පිළිබඳ සංකල්පය ද වේ.
අර්ථ දැක්වීම 6
නියැදි සම්මත අපගමනය-- සාමාන්ය විචලනයේ වර්ගමූලය:
\[(\sigma )_v=\sqrt(D_v)\]
නිවැරදි කළ විචලනය
නිවැරදි කළ විචලනය $S^2$ සොයා ගැනීමට, නියැදි විචලනය $\frac(n)(n-1)$ භාගයෙන් ගුණ කිරීම අවශ්ය වේ, i.e.
මෙම සංකල්පය නිවැරදි කරන ලද සම්මත අපගමනය පිළිබඳ සංකල්පය සමඟ ද සම්බන්ධ වේ, එය සූත්රය මගින් සොයාගත හැකිය:
ප්රභේදයේ අගය විවික්ත නොවන නමුත් කාල පරතරයන් වන විට, සාමාන්ය හෝ නියැදි විචල්යයන් ගණනය කිරීමේ සූත්රවල $x_i$ හි අගය $ වන පරතරයේ මැද අගය ලෙස ගනු ලැබේ. x_i.$ අයත් වේ
විචලනය සහ සම්මත අපගමනය සොයා ගැනීමේ ගැටලුවක උදාහරණයක්
උදාහරණ 1
නියැදි ජනගහනය පහත බෙදාහැරීමේ වගුව මගින් ලබා දී ඇත:
පින්තූරය 1.
ඒ සඳහා නියැදි විචලනය, නියැදි සම්මත අපගමනය, නිවැරදි කළ විචලනය සහ නිවැරදි කළ සම්මත අපගමනය සොයන්න.
මෙම ගැටළුව විසඳීම සඳහා, පළමුව අපි ගණනය කිරීමේ වගුවක් සාදන්නෙමු:
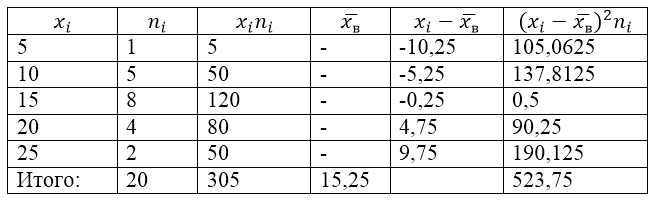
රූපය 2.
වගුවේ ඇති $\overline(x_v)$ (නියැදි සාමාන්යය) හි අගය සූත්රය මගින් සොයා ගැනේ:
\[\overline(x_in)=\frac(\sum\සීමා^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\සීමා^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15.25\]
සූත්රය භාවිතයෙන් නියැදි විචලනය සොයන්න:
නියැදි සම්මත අපගමනය:
\[(\sigma )_v=\sqrt(D_v)\ආසන්න වශයෙන් 5,12\]
නිවැරදි කළ විචලනය:
\[(S^2=\frac(n)(n-1)D)_v=\frac(20)(19)\cdot 26.1875\ආසන්න 27.57\]
සම්මත අපගමනය නිවැරදි කරන ලදී.
විචලනයේ වඩාත්ම පරිපූර්ණ ලක්ෂණය වන්නේ සම්මත අපගමනය වන අතර එය සම්මත (හෝ සම්මත අපගමනය) ලෙස හැඳින්වේ. සම්මත අපගමනය() ගණිතමය මධ්යන්යයෙන් තනි ලක්ෂණ අගයන්හි අපගමනයන්හි මධ්යන්ය වර්ග මූලයට සමාන වේ:
සම්මත අපගමනය සරලයි:


සමූහගත දත්ත සඳහා බරිත සම්මත අපගමනය යොදනු ලැබේ:

මූල අතර චතුරස්රය සහ මධ්යන්යය රේඛීය අපගමනයකොන්දේසි යටතේ සාමාන්ය බෙදාහැරීමේපහත අනුපාතය සිදු වේ: ~ 1.25.
සම්මත අපගමනය, විචලනයේ ප්රධාන නිරපේක්ෂ මිනුම වන අතර, සාමාන්ය බෙදාහැරීමේ වක්රයේ ඕඩිනේට් වල අගයන් නිර්ණය කිරීමේදී, නියැදි නිරීක්ෂණ සංවිධානයට අදාළ ගණනය කිරීම් වලදී සහ නියැදි ලක්ෂණවල නිරවද්යතාවය තහවුරු කිරීමේදී භාවිතා වේ. සමජාතීය ජනගහනයක ලක්ෂණයක විචලනයේ සීමාවන් තක්සේරු කිරීම.
විසුරුම, එහි වර්ග, සම්මත අපගමනය.
අහඹු විචල්යයක විචලනය- දී ඇති අහඹු විචල්යයක පැතිරීමේ මිනුමක්, එනම් එහි අපගමනය ගණිතමය අපේක්ෂාව. සංඛ්යා ලේඛනවල, තනතුර හෝ බොහෝ විට භාවිතා වේ. වර්ගමුලයවිචලනය සම්මත අපගමනය, සම්මත අපගමනය හෝ සම්මත පැතිරීම ලෙස හැඳින්වේ.
සම්පූර්ණ විචලනය (σ2) මෙම විචලනය ඇතිවීමට හේතු වූ සියලු සාධකවල බලපෑම යටතේ සමස්ත ජනගහනය තුළම ලක්ෂණයක විචලනය මනිනු ලැබේ. ඒ අතරම, කණ්ඩායම් ක්රමයට ස්තූතිවන්ත වන අතර, කණ්ඩායම් ලක්ෂණය හේතුවෙන් විචලනය හුදකලා කිරීමට සහ මැනිය හැකි අතර, ගණන් නොගත් සාධකවල බලපෑම යටතේ සිදුවන විචලනය.
අන්තර් කණ්ඩායම් විචලනය (σ 2 m.gr) ක්රමානුකූල විචලනය සංලක්ෂිත කරයි, එනම්, ලක්ෂණයේ බලපෑම යටතේ පැන නගින අධ්යයනය කරන ලද ලක්ෂණයේ විශාලත්වයේ වෙනස්කම් - කණ්ඩායම්කරණයට පාදක වන සාධකය.
සම්මත අපගමනය(සමාන පද: සම්මත අපගමනය, සම්මත අපගමනය, වර්ග අපගමනය; අදාළ නියමයන්: සම්මත අපගමනය, සම්මත පැතිරීම) - සම්භාවිතා න්යාය සහ සංඛ්යාලේඛන තුළ, එහි ගණිතමය අපේක්ෂාවට සාපේක්ෂව අහඹු විචල්යයක අගයන් විසුරුවා හැරීමේ වඩාත් පොදු දර්ශකය. සීමිත අගයන් සාම්පල සමඟ, ගණිතමය අපේක්ෂාව වෙනුවට, සාම්පල කට්ටලයේ අංක ගණිත මධ්යන්යය භාවිතා වේ.
සම්මත අපගමනය වඩාත්ම අහඹු විචල්යයේ ඒකක වලින් මනිනු ලබන අතර එය ගණනය කිරීමේදී භාවිතා වේ සම්මත දෝෂයක්අංක ගණිත මධ්යන්යය, ගොඩනඟන විට විශ්වාස කාලාන්තර, සංඛ්යානමය වශයෙන් උපකල්පන පරීක්ෂා කරන විට, අතර රේඛීය සම්බන්ධතාවයක් මනින විට අහඹු විචල්යයන්. එය සසම්භාවී විචල්යයක විචල්යයේ වර්ගමූලය ලෙස අර්ථ දැක්වේ.
සම්මත අපගමනය:

සම්මත අපගමනය(අහඹු විචල්යයක සම්මත අපගමනය ඇස්තමේන්තු කිරීම xඑහි විචලනය පිළිබඳ අපක්ෂපාතී ඇස්තමේන්තුවක් මත පදනම්ව එහි ගණිතමය අපේක්ෂාවට සාපේක්ෂව):

විසුරුම කොහෙද; - මම-වන නියැදි මූලද්රව්යය; - නියැදි ප්රමාණය; - නියැදියේ අංක ගණිත මධ්යන්යය:
![]()
ඇස්තමේන්තු දෙකම පක්ෂග්රාහී බව සැලකිල්ලට ගත යුතුය. හිදී සාමාන්ය නඩුවඅපක්ෂපාතී ඇස්තමේන්තුවක් ගොඩනගා ගත නොහැක. කෙසේ වෙතත්, අපක්ෂපාතී විචල්යතා ඇස්තමේන්තුවක් මත පදනම් වූ ඇස්තමේන්තුවක් අනුකූල වේ.
මාදිලිය සහ මධ්යන්ය නිර්ණය කිරීම සඳහා සාරය, විෂය පථය සහ ක්රියා පටිපාටිය.
විචල්ය ගුණාංගයක විශාලත්වයේ සාපේක්ෂ ලක්ෂණයක් සඳහා සංඛ්යාලේඛනවල බල-නීති සාමාන්යවලට අමතරව සහ අභ්යන්තර ව්යුහයබෙදාහැරීමේ ශ්රේණි ව්යුහාත්මක සාමාන්ය භාවිතා කරයි, ඒවා ප්රධාන වශයෙන් නිරූපණය කෙරේ මාදිලිය සහ මධ්යන්ය.
විලාසිතා- මෙය මාලාවේ වඩාත් පොදු ප්රභේදයයි. උදාහරණයක් ලෙස, ගැනුම්කරුවන් අතර වැඩිම ඉල්ලුමක් ඇති ඇඳුම්, සපත්තු ප්රමාණය තීරණය කිරීමේදී විලාසිතා භාවිතා වේ. විවික්ත ශ්රේණියක් සඳහා වන මාදිලිය යනු ඉහළම සංඛ්යාතය සහිත ප්රභේදයයි. පරතරය සඳහා මාදිලිය ගණනය කිරීමේදී විචලනය මාලාවක්පළමුව මාදිලියේ පරතරය (උපරිම සංඛ්යාතය අනුව) තීරණය කිරීම අවශ්ය වේ, පසුව සූත්රය අනුව ගුණාංගයේ මාදිලියේ අගයේ අගය:

- - විලාසිතා වටිනාකම
- - මාදිලියේ පරතරයේ පහළ සීමාව
- - විරාම අගය
- - මාදිලි විරාම සංඛ්යාතය
- - මාදිලියට පෙර විරාමයේ සංඛ්යාතය
- - මාදිලියෙන් පසු විරාමයේ වාර ගණන
මධ්යස්ථ -ශ්රේණිගත ශ්රේණියට යටින් පවතින විශේෂාංගයේ අගය මෙය වන අතර මෙම ශ්රේණිය සංඛ්යාවෙන් සමාන කොටස් දෙකකට බෙදා ඇත.
තුළ මධ්යන්ය තීරණය කිරීමට විවික්ත මාලාවක්සංඛ්යාත ඉදිරියේ, සංඛ්යාතවල අර්ධ එකතුව පළමුව ගණනය කරනු ලබන අතර, පසුව එය මතට වැටෙන ප්රභේදයේ අගය තීරණය කරනු ලැබේ. (අනුපිළිවෙළට සකසන ලද පේළියේ ඔත්තේ විශේෂාංග සංඛ්යාවක් තිබේ නම්, මධ්ය අංකය සූත්රය මගින් ගණනය කෙරේ:
M e \u003d (n (සමස්තයේ ඇති විශේෂාංග ගණන) + 1) / 2,
ලක්ෂණ ඉරට්ටේ සංඛ්යාවකදී, මධ්යස්ථය පේළියේ මැද ඇති ලක්ෂණ දෙකේ සාමාන්යයට සමාන වේ).
ගණනය කරන විට මධ්යන්යවිරාම විචල්ය ශ්රේණියක් සඳහා, පළමුව මධ්යස්ථය පිහිටා ඇති මධ්ය පරතරය තීරණය කරන්න, පසුව සූත්රය අනුව මධ්යයේ අගය තීරණය කරන්න:

- අපේක්ෂිත මධ්යන්ය වේ
- මධ්යස්ථය අඩංගු අන්තරයේ පහළ මායිම වේ
- - විරාම අගය
- - සංඛ්යාතවල එකතුව හෝ මාලාවේ සාමාජිකයන් සංඛ්යාව
මධ්යයට පෙර ඇති විරාමවල සමුච්චිත සංඛ්යාතවල එකතුව
- මධ්යස්ථ අන්තරයේ සංඛ්යාතය වේ
උදාහරණයක්. මාදිලිය සහ මධ්යන්ය සොයන්න.
විසඳුමක්:
හිදී මෙම උදාහරණයමෙම කාල පරතරය ඉහළම සංඛ්යාතය (1054) සඳහා හේතු වන බැවින්, මාදිලි පරතරය අවුරුදු 25-30 අතර වයස් කාණ්ඩය තුළ වේ.
මාදිලියේ අගය ගණනය කරමු:
මෙයින් අදහස් කරන්නේ සිසුන්ගේ මාදිලියේ වයස අවුරුදු 27 ක් බවයි.
මධ්යන්ය ගණනය කරන්න. මධ්ය පරතරය අවුරුදු 25-30 අතර වයස් කාණ්ඩයේ වේ, මන්ද මෙම කාල පරතරය තුළ ජනගහනය සමාන කොටස් දෙකකට බෙදන ප්රභේදයක් ඇත (Σf i /2 = 3462/2 = 1731). ඊළඟට, අපි අවශ්ය සංඛ්යාත්මක දත්ත සූත්රයට ආදේශ කර මධ්යයේ අගය ලබා ගනිමු:

මෙයින් අදහස් කරන්නේ සිසුන්ගෙන් අඩක් වයස අවුරුදු 27.4 ට අඩු වන අතර අනෙක් භාගය අවුරුදු 27.4 ට වැඩි බවයි.
මාදිලියට සහ මධ්යයට අමතරව, quartiles වැනි දර්ශක භාවිතා කළ හැක, ශ්රේණිගත ශ්රේණි සමාන කොටස් 4 කට බෙදීම, දශමයන්- කොටස් 10 ක් සහ ප්රතිශත - කොටස් 100 කට.
වරණාත්මක නිරීක්ෂණ සංකල්පය සහ එහි විෂය පථය.
වරණාත්මක නිරීක්ෂණයඅඛණ්ඩ නිරීක්ෂණ යොදන විට අදාළ වේ භෞතිකව කළ නොහැකි යවිශාල දත්ත ප්රමාණයක් නිසා හෝ ආර්ථික වශයෙන් ප්රායෝගික නැත. භෞතික නොහැකියාව ඇතිවේ, නිදසුනක් වශයෙන්, මගී ප්රවාහයන් අධ්යයනය කරන විට, වෙළෙඳපොළ මිල, පවුලේ අයවැය. ඔවුන්ගේ විනාශයට සම්බන්ධ භාණ්ඩවල ගුණාත්මකභාවය තක්සේරු කිරීමේදී ආර්ථික අකාර්යක්ෂමතාව සිදු වේ, උදාහරණයක් ලෙස, රස බැලීම, ශක්තිය සඳහා ගඩොල් පරීක්ෂා කිරීම යනාදිය.
නිරීක්ෂණ සඳහා තෝරාගත් සංඛ්යාන ඒකක නියැදියක් හෝ නියැදියක් සෑදී ඇති අතර ඒවායේ සම්පූර්ණ අරාව - සාමාන්ය ජනගහනය (GS). මෙම අවස්ථාවේදී, නියැදියේ ඒකක ගණන දක්වයි n, සහ සමස්ත HS හි - එන්. ආකල්පය n/Nසාම්පලයේ සාපේක්ෂ විශාලත්වය හෝ අනුපාතය ලෙස හැඳින්වේ.
නියැදීමේ ප්රතිඵලවල ගුණාත්මක භාවය රඳා පවතින්නේ නියැදියේ නියෝජනත්වය මත ය, එනම් HS හි එය කෙතරම් නියෝජනය වේ ද යන්නයි. නියැදියේ නියෝජිතත්වය සහතික කිරීම සඳහා, එය නිරීක්ෂණය කිරීම අවශ්ය වේ ඒකක අහඹු තේරීමේ මූලධර්මය, නියැදියට HS ඒකකයක් ඇතුළත් කිරීම අහඹු ලෙස හැර වෙනත් කිසිදු සාධකයකින් බලපෑම් කළ නොහැකි බව උපකල්පනය කරයි.
පවතී අහඹු තේරීමේ ක්රම 4 ක්නියැදි කිරීමට:
- ඇත්තටම අහඹුසංඛ්යාලේඛන පවරන විට තේරීම හෝ "ලොටෝ ක්රමය" අනුක්රමික අංක, යම් යම් වස්තූන් මත ගෙන එන ලද (උදාහරණයක් ලෙස, kegs), පසුව යම් බහාලුම් (උදාහරණයක් ලෙස, බෑගයක) මිශ්ර කර අහඹු ලෙස තෝරා ගනු ලැබේ. ප්රායෝගිකව, මෙම ක්රමය අහඹු සංඛ්යා උත්පාදක යන්ත්රයක් හෝ අහඹු සංඛ්යා ගණිතමය වගු භාවිතයෙන් සිදු කෙරේ.
- යාන්ත්රිකතෝරාගැනීම, ඒ අනුව ( N/n)-සාමාන්ය ජනගහනයේ අගය. උදාහරණයක් ලෙස, එහි අගයන් 100,000ක් තිබේ නම් සහ ඔබට 1,000ක් තෝරා ගැනීමට අවශ්ය නම්, සෑම 100,000 / 1000 = 100 වැනි අගයක්ම නියැදියට වැටේ. එපමණක්ද නොව, ඒවා ශ්රේණිගත කර නොමැති නම්, පළමු එක පළමු සියයෙන් අහඹු ලෙස තෝරාගෙන ඇති අතර අනෙක් අයගේ සංඛ්යාව තවත් සියයක් වනු ඇත. උදාහරණයක් ලෙස, ඒකක අංක 19 පළමු නම්, අංක 119 ඊළඟ විය යුතුය, පසුව අංක 219, පසුව අංක 319, සහ යනාදිය. ජනගහන ඒකක ශ්රේණිගත කර ඇත්නම්, පළමුව #50, පසුව #150, ඉන්පසු #250, සහ යනාදිය තෝරා ගනු ලැබේ.
- විෂමජාතීය දත්ත අරාවකින් අගයන් තෝරාගැනීම සිදු කෙරේ ස්ථරීකෘත(ස්ථරගත) ක්රමය, සාමාන්ය ජනගහනය කලින් සමජාතීය කණ්ඩායම්වලට බෙදා ඇති විට, අහඹු හෝ යාන්ත්රික තෝරා ගැනීමක් යෙදේ.
- විශේෂ නියැදීමේ ක්රමයකි මාලාවතෝරා ගැනීම, තනි ප්රමාණ අහඹු ලෙස හෝ යාන්ත්රිකව තෝරා නොගන්නා නමුත්, ඒවායේ ශ්රේණි (සමහර සංඛ්යාවක සිට පේළියක සමහරක් දක්වා අනුපිළිවෙල), අඛණ්ඩ නිරීක්ෂණ සිදු කරනු ලැබේ.
නියැදි නිරීක්ෂණවල ගුණාත්මකභාවය ද රඳා පවතී නියැදි වර්ගය: නැවත නැවතත්හෝ පුනරාවර්තන නොවන.
හිදී නැවත තෝරා ගැනීමනියැදියට වැටුණු සංඛ්යානමය අගයන් හෝ ඒවායේ ශ්රේණි භාවිතයෙන් පසු සාමාන්ය ජනතාව වෙත නැවත ලබා දෙන අතර, නව නියැදියකට ඇතුල් වීමට අවස්ථාවක් ලැබේ. ඒ අතරම, සාමාන්ය ජනගහනයේ සියලුම අගයන් නියැදියට ඇතුළත් කිරීමට සමාන සම්භාවිතාවක් ඇත.
පුනරාවර්තන නොවන තේරීමඑයින් අදහස් වන්නේ නියැදියට ඇතුළත් කර ඇති සංඛ්යානමය අගයන් හෝ ඒවායේ ශ්රේණි භාවිතයෙන් පසු සාමාන්ය ජනතාව වෙත ආපසු ලබා නොදෙන අතර එම නිසා ඊළඟ නියැදියට ඇතුළු වීමේ සම්භාවිතාව පසුකාලීන ඉතිරි අගයන් සඳහා වැඩි වන බවයි.
පුනරාවර්තන නොවන තේරීම වැඩිපුර ලබා දෙයි නිවැරදි ප්රතිඵලඑබැවින් නිතර නිතර භාවිතා වේ. නමුත් එය යෙදිය නොහැකි අවස්ථා තිබේ (මගී ප්රවාහ අධ්යයනය, පාරිභෝගික ඉල්ලුම ආදිය) පසුව නැවත තෝරා ගැනීමක් සිදු කෙරේ.
නිරීක්ෂණ නියැදියේ ආන්තික දෝෂය, සාම්පලයේ සාමාන්ය දෝෂය, ඒවා ගණනය කරනු ලබන අනුපිළිවෙල.
නියැදි ජනගහනයක් සෑදීමේ ඉහත ක්රම සහ මෙම නඩුවේ පැන නගින දෝෂ පිළිබඳව අපි විස්තරාත්මකව සලකා බලමු. නියෝජනය .
ඇත්ත වශයෙන්ම - අහඹුනියැදිය පදනම් වී ඇත්තේ සාමාන්ය ජනගහණයෙන් ඒකක තෝරා ගැනීම මත අහඹු ලෙස අනුකූලතාවයේ කිසිදු අංගයක් නොමැතිව ය. තාක්ෂණික වශයෙන්, නිසි අහඹු තේරීම සිදු කරනු ලබන්නේ කැබලි අක්ෂර ඇඳීමෙන් (උදාහරණයක් ලෙස, ලොතරැයි) හෝ අහඹු අංක වගුවක් මගිනි.
නිසි අහඹු තේරීම පිරිසිදු ස්වරූපය» වරණාත්මක නිරීක්ෂණ භාවිතයේ දී කලාතුරකින් භාවිතා වේ, නමුත් එය අනෙකුත් තේරීම් වර්ග අතර ආරම්භක වේ, එය වරණාත්මක නිරීක්ෂණයේ මූලික මූලධර්ම ක්රියාත්මක කරයි. සරල අහඹු නියැදියක් සඳහා නියැදි ක්රමයේ න්යාය සහ දෝෂ සූත්රය පිළිබඳ ප්රශ්න කිහිපයක් අපි සලකා බලමු.
නියැදි දෝෂයක්- මෙය සාමාන්ය ජනගහනයේ පරාමිතියේ අගය සහ නියැදි නිරීක්ෂණ ප්රතිඵල වලින් ගණනය කරන ලද එහි අගය අතර වෙනසයි. සාමාන්ය ප්රමාණාත්මක ලක්ෂණයක් සඳහා, නියැදි දෝෂය තීරණය කරනු ලැබේ
දර්ශකය ආන්තික නියැදීමේ දෝෂය ලෙස හැඳින්වේ.
නියැදි මධ්යන්යය යනු ගත හැකි අහඹු විචල්යයකි විවිධ අර්ථනියැදියට ඇතුළත් කර ඇති ඒකක මත පදනම්ව. එබැවින්, නියැදි දෝෂ ද අහඹු විචල්ය වන අතර විවිධ අගයන් ගත හැකිය. එබැවින්, සාමාන්යය තීරණය වේ විය හැකි දෝෂ - නියැදි දෝෂයක් අදහස් වේ, රඳා පවතින්නේ:
නියැදි ප්රමාණය: විශාල සංඛ්යාවක්, කුඩා සාමාන්ය දෝෂය;
අධ්යයනය කරන ලද ලක්ෂණයේ වෙනස් වීමේ මට්ටම: ගතිලක්ෂණයේ විචලනය කුඩා වන අතර, ඒ අනුව, විචලනය, අඩු වේ වැරදි අදහස්සාම්පල.
හිදී අහඹු ලෙස නැවත තෝරා ගැනීමසාමාන්ය දෝෂය ගණනය කරනු ලැබේ:
.
ප්රායෝගිකව, සාමාන්ය විචලනය හරියටම දන්නේ නැත, නමුත් තුළ සම්භාවිතා න්යායකියලා ඔප්පු කළා ![]() .
.
ප්රමාණවත් තරම් විශාල n සඳහා අගය 1 ට ආසන්න බැවින්, අපට එය උපකල්පනය කළ හැකිය. එවිට මධ්යන්ය නියැදි දෝෂය ගණනය කළ හැක:
.
නමුත් කුඩා නියැදියක (n සඳහා<30) коэффициент необходимо учитывать, и среднюю ошибку малой выборки рассчитывать по формуле  .
.
හිදී අහඹු නියැදීමලබා දී ඇති සූත්ර අගය මගින් නිවැරදි කරනු ලැබේ. එවිට නියැදි නොකිරීමේ සාමාන්ය දෝෂය වන්නේ:  හා
හා  .
.
නිසා සෑම විටම ට වඩා අඩු වේ, එවිට සාධකය () සෑම විටම 1 ට වඩා අඩු වේ. මෙයින් අදහස් කරන්නේ පුනරාවර්තන නොවන තේරීමේ සාමාන්ය දෝෂය නැවත නැවත තේරීමට වඩා අඩු බවයි.
යාන්ත්රික නියැදීමසාමාන්ය ජනගහනය යම් ආකාරයකින් ඇණවුම් කළ විට භාවිතා වේ (උදාහරණයක් ලෙස, අකාරාදී පිළිවෙලට ඡන්ද හිමි නාමලේඛන, දුරකථන අංක, නිවාස අංක, මහල් නිවාස). ඒකක තෝරාගැනීම නිශ්චිත කාල පරතරයකින් සිදු කරනු ලැබේ, එය නියැදියේ ප්රතිශතයේ අන්යෝන්ය අගයට සමාන වේ. එබැවින්, 2% සාම්පලයක් සමඟ, සෑම ඒකක 50 ක් = 1 / 0.02 තෝරා ගනු ලැබේ, 5% බැගින්, සාමාන්ය ජනගහනයේ ඒකක 1 / 0.05 = 20 බැගින්.
මූලාරම්භය විවිධ ආකාරවලින් තෝරා ඇත: අහඹු ලෙස, අන්තරයේ මැද සිට, ආරම්භයේ වෙනසක් සමඟ. ප්රධාන දෙය වන්නේ ක්රමානුකූල දෝෂ වළක්වා ගැනීමයි. උදාහරණයක් ලෙස, 5% සාම්පලයක් සමඟ, 13 වැනි පළමු ඒකකය ලෙස තෝරාගෙන තිබේ නම්, ඊළඟ 33, 53, 73, ආදිය.
නිරවද්යතාවය අනුව, යාන්ත්රික තේරීම නිසි අහඹු නියැදීමකට ආසන්න වේ. එබැවින්, යාන්ත්රික නියැදීමේ සාමාන්ය දෝෂය තීරණය කිරීම සඳහා, නිසි අහඹු තේරීමේ සූත්ර භාවිතා කරනු ලැබේ.
හිදී සාමාන්ය තේරීම සමීක්ෂණයට ලක් කරන ලද ජනගහනය මූලික වශයෙන් සමජාතීය, තනි වර්ගයේ කණ්ඩායම් වලට බෙදා ඇත. උදාහරණයක් ලෙස, ව්යවසායන් මැන බැලීමේදී, මේවා කර්මාන්ත, උප අංශ, ජනගහනය අධ්යයනය කරන විට - ප්රදේශ, සමාජ හෝ වයස් කාණ්ඩ විය හැකිය. එවිට එක් එක් කණ්ඩායමෙන් යාන්ත්රික හෝ නිසි අහඹු ආකාරයෙන් ස්වාධීන තේරීමක් සිදු කරනු ලැබේ.
සාමාන්ය නියැදීම අනෙකුත් ක්රමවලට වඩා නිවැරදි ප්රතිඵල ලබා දෙයි. සාමාන්ය ජනගහනයේ ටයිප් කිරීම නියැදියේ එක් එක් ටයිපොලොජිකල් කණ්ඩායම නියෝජනය කිරීම සහතික කරයි, එමඟින් සාමාන්ය නියැදි දෝෂය මත අන්තර් කණ්ඩායම් විචල්යයේ බලපෑම බැහැර කිරීමට හැකි වේ. එබැවින්, විචල්ය එකතු කිරීමේ රීතියට අනුව සාමාන්ය නියැදියක දෝෂය සොයා ගැනීමේදී (), කණ්ඩායම් විචල්යයන්ගේ සාමාන්යය පමණක් සැලකිල්ලට ගත යුතුය. එවිට මධ්යන්ය නියැදි දෝෂය වන්නේ:
නැවත තෝරාගැනීමේදී
,
පුනරාවර්තන නොවන තේරීම සමඟ  ,
,
කොහෙද  නියැදියේ අන්තර්-කණ්ඩායම් විචල්යයන්ගේ මධ්යන්යය වේ.
නියැදියේ අන්තර්-කණ්ඩායම් විචල්යයන්ගේ මධ්යන්යය වේ.
අනුක්රමික (හෝ කැදලි) තේරීම
නියැදි සමීක්ෂණය ආරම්භ කිරීමට පෙර ජනගහනය ශ්රේණි හෝ කණ්ඩායම්වලට බෙදා ඇති විට භාවිතා වේ. මෙම මාලාව නිමි භාණ්ඩ, ශිෂ්ය කණ්ඩායම්, කණ්ඩායම්වල පැකේජ විය හැකිය. විභාගය සඳහා ශ්රේණි යාන්ත්රිකව හෝ අහඹු ලෙස තෝරා ගනු ලබන අතර මාලාව තුළ ඒකක පිළිබඳ සම්පූර්ණ සමීක්ෂණයක් සිදු කරනු ලැබේ. එබැවින්, සාමාන්ය නියැදි දෝෂය රඳා පවතින්නේ සූත්රය මගින් ගණනය කරනු ලබන අන්තර් කණ්ඩායම් (අන්තර් ශ්රේණි) විචලනය මත පමණි: 
r යනු තෝරාගත් ශ්රේණි ගණන;
- i-th ශ්රේණියේ සාමාන්යය.
සාමාන්ය අනුක්රමික නියැදීමේ දෝෂය ගණනය කෙරේ:
නැවත තෝරාගත් විට:
,
පුනරාවර්තන නොවන තේරීම සමඟ:  ,
,
මෙහි R යනු ශ්රේණිවල මුළු සංඛ්යාවයි.
ඒකාබද්ධතෝරා ගැනීමතෝරා ගැනීමේ සලකා බලන ලද ක්රමවල එකතුවකි.
ඕනෑම තේරීමක් ක්රමයක් සඳහා සාමාන්ය නියැදීමේ දෝෂය ප්රධාන වශයෙන් නියැදියේ නිරපේක්ෂ ප්රමාණය මත රඳා පවතින අතර, අඩු වශයෙන්, නියැදියේ ප්රතිශතය මත රඳා පවතී. ඒකක 4,500 ක ජනගහනයකින් පළමු අවස්ථාවේ දී නිරීක්ෂණ 225 ක් සහ දෙවන අවස්ථාවේ දී ඒකක 225,000 කින් නිරීක්ෂණ සිදු කර ඇතැයි සිතමු. අවස්ථා දෙකෙහිම විචල්යයන් 25 ට සමාන වේ. එවිට, පළමු අවස්ථාවේ දී, 5% තේරීමක් සමඟ, නියැදි දෝෂය වනුයේ: 
දෙවන අවස්ථාවේදී, 0.1% තේරීමක් සමඟ, එය සමාන වනු ඇත:

මේ ක්රමයෙන්, නියැදි ප්රතිශතය 50 ගුණයකින් අඩු වීමත් සමඟ, නියැදි ප්රමාණය වෙනස් නොවූ බැවින් නියැදි දෝෂය තරමක් වැඩි විය.
නියැදි ප්රමාණය නිරීක්ෂණ 625 දක්වා වැඩි වී ඇතැයි උපකල්පනය කරන්න. මෙම අවස්ථාවේදී, නියැදීමේ දෝෂය වන්නේ: 
සාමාන්ය ජනගහනයේ එකම ප්රමාණය සමඟ නියැදිය 2.8 ගුණයකින් වැඩි වීම නියැදි දෝෂයේ ප්රමාණය 1.6 ගුණයකට වඩා අඩු කරයි.
නියැදි ජනගහනයක් සෑදීමේ ක්රම සහ ක්රම.
සංඛ්යාලේඛනවලදී, නියැදි කට්ටල සෑදීමේ විවිධ ක්රම භාවිතා කරනු ලැබේ, එය අධ්යයනයේ අරමුණු අනුව තීරණය වන අතර අධ්යයනයේ වස්තුවේ විශේෂතා මත රඳා පවතී.
නියැදි සමීක්ෂණයක් පැවැත්වීම සඳහා ප්රධාන කොන්දේසිය වන්නේ සාමාන්ය ජනගහනයේ සෑම ඒකකයකටම නියැදියට ඇතුළු වීමට සමාන අවස්ථා පිළිබඳ මූලධර්මය උල්ලංඝනය කිරීමෙන් පැන නගින ක්රමානුකූල දෝෂ ඇතිවීම වැළැක්වීමයි. නියැදි ජනගහනයක් ගොඩනැගීම සඳහා විද්යාත්මකව පදනම් වූ ක්රම භාවිතා කිරීමේ ප්රතිඵලයක් ලෙස ක්රමානුකූල දෝෂ වැළැක්වීම සාක්ෂාත් කරගනු ලැබේ.
සාමාන්ය ජනගහනයෙන් ඒකක තෝරා ගැනීමට පහත ක්රම තිබේ:
1) තනි තේරීම - නියැදියේ තනි ඒකක තෝරා ගනු ලැබේ;
2) කණ්ඩායම් තේරීම - ගුණාත්මකව සමජාතීය කණ්ඩායම් හෝ අධ්යයනය යටතේ පවතින ඒකක මාලාව නියැදියට වැටේ;
3) ඒකාබද්ධ තේරීම යනු තනි සහ කණ්ඩායම් තේරීමේ එකතුවකි.
තෝරා ගැනීමේ ක්රම තීරණය කරනු ලබන්නේ නියැදීම් ජනගහනය ගොඩනැගීම සඳහා නීති රීති මගිනි.
නියැදිය විය හැක්කේ:
- නිසි අහඹුසාමාන්ය ජනගහනයෙන් තනි ඒකක අහඹු ලෙස (නොදැනුවත්ව) තෝරාගැනීමේ ප්රතිඵලයක් ලෙස නියැදිය සෑදී ඇත. මෙම අවස්ථාවෙහිදී, නියැදි කට්ටලයේ තෝරාගත් ඒකක ගණන සාමාන්යයෙන් නියැදියේ පිළිගත් අනුපාතය මත තීරණය වේ. නියැදි කොටස යනු නියැදි ජනගහනයේ ඒකක සංඛ්යාවේ අනුපාතයයි n සාමාන්ය ජනගහනයේ ඒකක ගණනට, i.e.
- යාන්ත්රිකනියැදියේ ඒකක තෝරා ගැනීම සාමාන්ය ජනගහනයෙන් සිදු කර ඇති අතර එය සමාන කාල පරතරයන්ට (කණ්ඩායම්) බෙදා ඇත. මෙම අවස්ථාවෙහිදී, සාමාන්ය ජනගහනයේ පරතරයේ විශාලත්වය නියැදියේ සමානුපාතිකයේ ප්රතිවර්තයට සමාන වේ. එබැවින්, 2% නියැදියක් සමඟ, සෑම 50 වන ඒකකයක්ම තෝරා ගනු ලැබේ (1:0.02), 5% නියැදියක් සමඟ, සෑම 20 වන ඒකක (1:0.05) ආදිය. මේ අනුව, තෝරා ගැනීමේ පිළිගත් අනුපාතයට අනුකූලව, සාමාන්ය ජනගහනය යාන්ත්රිකව සමාන කණ්ඩායම් වලට බෙදා ඇත. නියැදියේ එක් කණ්ඩායමකින් තෝරාගනු ලබන්නේ එක් ඒකකයක් පමණි.
- සාමාන්ය -එහිදී සාමාන්ය ජනගහනය මුලින්ම සමජාතීය සාමාන්ය කණ්ඩායම්වලට බෙදා ඇත. ඉන්පසුව, එක් එක් සාමාන්ය කණ්ඩායමකින්, නියැදියට ඒකක තනි තේරීමක් අහඹු හෝ යාන්ත්රික නියැදියක් මගින් සිදු කෙරේ. සාමාන්ය නියැදියක වැදගත් ලක්ෂණයක් වන්නේ නියැදියක ඒකක තෝරාගැනීමේ වෙනත් ක්රමවලට සාපේක්ෂව වඩා නිවැරදි ප්රතිඵල ලබා දීමයි;
- මාලාව- සාමාන්ය ජනගහනය එකම ප්රමාණයේ කණ්ඩායම් වලට බෙදා ඇත - ශ්රේණිය. නියැදි කට්ටලය තුළ මාලාව තෝරා ඇත. මාලාව තුළ, මාලාවට වැටුණු ඒකක අඛණ්ඩ නිරීක්ෂණයක් සිදු කරනු ලැබේ;
- ඒකාබද්ධ- නියැදීම අදියර දෙකකින් විය හැකිය. මෙහිදී සාමාන්ය ජනතාව ප්රථමයෙන් කණ්ඩායම්වලට බෙදා ඇත. ඉන්පසු කණ්ඩායම් තෝරා ගනු ලබන අතර, දෙවැන්න තුළ තනි ඒකක තෝරා ගනු ලැබේ.
සංඛ්යාලේඛනවලදී, නියැදියක ඒකක තෝරා ගැනීමේ පහත ක්රම වෙන්කර හඳුනාගත හැකිය::
- තනි අදියරනියැදිය - තෝරාගත් සෑම ඒකකයක්ම ලබා දී ඇති පදනම මත වහාම අධ්යයනයට ලක් කෙරේ (ඇත්ත වශයෙන්ම අහඹු සහ අනුක්රමික සාම්පල);
- බහු අදියරනියැදීම - තේරීම සිදු කරනු ලබන්නේ තනි කණ්ඩායම්වල සාමාන්ය ජනගහනයෙන් වන අතර තනි ඒකක කණ්ඩායම් වලින් තෝරා ගනු ලැබේ (නියැදි ජනගහනයේ ඒකක තෝරා ගැනීමේ යාන්ත්රික ක්රමයක් සහිත සාමාන්ය නියැදියක්).
මීට අමතරව, ඇත:
- නැවත තෝරා ගැනීම- ආපසු පන්දුවේ යෝජනා ක්රමය අනුව. මෙම අවස්ථාවෙහිදී, නියැදියට වැටී ඇති සෑම ඒකකයක් හෝ මාලාවක්ම සාමාන්ය ජනතාව වෙත ආපසු ලබා දෙන අතර එබැවින් නැවත නියැදියට ඇතුළත් කිරීමට අවස්ථාවක් තිබේ;
- පුනරාවර්තන නොවන තේරීම- ආපසු නොඑන පන්දුවේ යෝජනා ක්රමය අනුව. එය එකම නියැදි ප්රමාණය සඳහා වඩාත් නිවැරදි ප්රතිඵල ඇත.
අවශ්ය නියැදි ප්රමාණය තීරණය කිරීම (ශිෂ්ය වගුව භාවිතා කිරීම).
නියැදීමේ සිද්ධාන්තයේ එක් විද්යාත්මක මූලධර්මයක් වන්නේ ප්රමාණවත් ඒකක සංඛ්යාවක් තෝරාගෙන ඇති බව සහතික කිරීමයි. න්යායාත්මකව, මෙම මූලධර්මයට අනුකූල වීමේ අවශ්යතාවය සම්භාවිතා න්යායේ සීමිත ප්රමේයවල සාක්ෂිවල ඉදිරිපත් කර ඇති අතර, එමඟින් සාමාන්ය ජනගහනයෙන් ඒකක කීයක් තෝරා ගත යුතුද යන්න තහවුරු කිරීමට ඔබට ඉඩ සලසයි, එවිට එය ප්රමාණවත් වන අතර නියැදියේ නියෝජිතත්වය සහතික කරයි.
නියැදියේ සම්මත දෝෂයේ අඩු වීමක් සහ, ඒ අනුව, ඇස්තමේන්තු වල නිරවද්යතාවයේ වැඩි වීමක් සෑම විටම නියැදි ප්රමාණයේ වැඩි වීමක් සමඟ සම්බන්ධ වේ, එබැවින්, දැනටමත් නියැදි නිරීක්ෂණයක් සංවිධානය කිරීමේ අදියරේදී තීරණය කිරීම අවශ්ය වේ. නිරීක්ෂණ ප්රතිඵලවල අවශ්ය නිරවද්යතාව සහතික කිරීම සඳහා නියැදි ප්රමාණය කුමක් විය යුතුද? අවශ්ය නියැදි ප්රමාණය ගණනය කිරීම, ආන්තික නියැදීම් දෝෂ (A) සඳහා සූත්ර වලින් ලබාගත් සූත්ර භාවිතයෙන් ගොඩනගා ඇත, එක් හෝ තවත් වර්ගයකට සහ තෝරාගැනීමේ ක්රමයට අනුරූප වේ. එබැවින්, අහඹු පුනරාවර්තන නියැදි ප්රමාණය (n) සඳහා, අපට ඇත්තේ:

මෙම සූත්රයේ සාරය නම්, අවශ්ය සංඛ්යාව අහඹු ලෙස නැවත තෝරා ගැනීමත් සමඟ, නියැදි ප්රමාණය විශ්වාස සංගුණකයේ වර්ගයට සෘජුව සමානුපාතික වීමයි. (t2)සහ විචල්ය ලක්ෂණයේ විචලනය (?2) සහ ආන්තික නියැදි දෝෂයේ (?2) වර්ගයට ප්රතිලෝමව සමානුපාතික වේ. විශේෂයෙන්ම, ආන්තික දෝෂය දෙගුණ කිරීමෙන්, අවශ්ය නියැදි ප්රමාණය හතර ගුණයකින් අඩු කළ හැකිය. පරාමිති තුනෙන්, දෙකක් (t සහ?) පර්යේෂකයා විසින් සකසා ඇත.
ඒ අතරම, පර්යේෂකයානියැදි සමීක්ෂණයේ අරමුණු සඳහා, ප්රශ්නය තීරණය කළ යුතුය: ප්රශස්ත ප්රභේදය ලබා දීම සඳහා මෙම පරාමිතීන් ඇතුළත් කිරීමට වඩා හොඳ ප්රමාණාත්මක සංයෝජනය කුමක්ද? එක් අවස්ථාවක, ඔහු ලබා ගත් ප්රතිඵලවල විශ්වසනීයත්වය (t) නිරවද්යතාව (?) මිනුමට වඩා සෑහීමකට පත් විය හැකිය, අනෙක් - අනෙක් අතට. ආන්තික නියැදීමේ දෝෂයේ වටිනාකම පිළිබඳ ගැටළුව විසඳීම වඩා දුෂ්කර ය, නියැදි නිරීක්ෂණයක් සැලසුම් කිරීමේ අදියරේදී පර්යේෂකයාට මෙම දර්ශකය නොමැති බැවින්, ප්රායෝගිකව, ආන්තික නියැදීමේ දෝෂය සැකසීම සිරිතකි. රීතියක්, ලක්ෂණයේ අපේක්ෂිත සාමාන්ය මට්ටමෙන් 10%ක් ඇතුළත. උපකල්පිත සාමාන්ය මට්ටමක් ස්ථාපිත කිරීම විවිධ ආකාරවලින් ප්රවේශ විය හැකිය: සමාන පෙර සමීක්ෂණ වලින් දත්ත භාවිතා කිරීම, හෝ නියැදි රාමුවෙන් දත්ත භාවිතා කිරීම සහ කුඩා නියමු නියැදියක් ගැනීම.
නියැදි නිරීක්ෂණ සැලසුම් කිරීමේදී ස්ථාපනය කිරීමට වඩාත්ම දුෂ්කර දෙය වන්නේ සූත්රයේ (5.2) තුන්වන පරාමිතියයි - නියැදි ජනගහනයේ විචලනය. මෙම අවස්ථාවෙහිදී, පෙර සමාන හා නියමු සමීක්ෂණ වලින් ලබාගත් විමර්ශකයාට ලබා ගත හැකි සියලු තොරතුරු භාවිතා කිරීම අවශ්ය වේ.
නිර්වචනය පිළිබඳ ප්රශ්නයනියැදි සමීක්ෂණයට නියැදි ඒකකවල ලක්ෂණ කිහිපයක් අධ්යයනය කිරීම ඇතුළත් නම් අවශ්ය නියැදි ප්රමාණය වඩාත් සංකීර්ණ වේ. මෙම අවස්ථාවෙහිදී, එක් එක් ලක්ෂණවල සාමාන්ය මට්ටම් සහ ඒවායේ විචලනය, රීතියක් ලෙස, වෙනස් වන අතර, එබැවින් අරමුණ සහ අරමුණු සැලකිල්ලට ගනිමින් මනාප ලබා දිය යුත්තේ කුමන ලක්ෂණ වලින් කුමන විසරණයටද යන්න තීරණය කළ හැකිය. සමීක්ෂණය.
නියැදි නිරීක්ෂණයක් සැලසුම් කිරීමේදී, යම් අධ්යයනයක අරමුණු සහ නිරීක්ෂණ ප්රතිඵල මත පදනම්ව නිගමනවල සම්භාවිතාව අනුව අවසර ලත් නියැදි දෝෂයේ පූර්ව නිශ්චිත අගයක් උපකල්පනය කෙරේ.
සාමාන්යයෙන්, නියැදි මධ්යන්ය අගයෙහි ආන්තික දෝෂය සඳහා සූත්රය ඔබට තීරණය කිරීමට ඉඩ සලසයි:
නියැදි ජනගහනයේ දර්ශක වලින් සාමාන්ය ජනගහනයේ දර්ශකවල ඇති විය හැකි අපගමනයන්හි විශාලත්වය;
අවශ්ය නියැදි ප්රමාණය, අවශ්ය නිරවද්යතාවය සැපයීම, සිදුවිය හැකි දෝෂයක සීමාවන් නිශ්චිත අගයක් නොඉක්මවනු ඇත;
නියැදියේ දෝෂයට දී ඇති සීමාවක් තිබීමේ සම්භාවිතාව.
ශිෂ්ය බෙදාහැරීමසම්භාවිතා න්යාය අනුව, එය පරම අඛණ්ඩ ව්යාප්ති එක් පරාමිති පවුලකි.
ගතික ශ්රේණි (විරාමය, මොහොත), ගතික ශ්රේණි වසා දැමීම.
ගතික මාලාව- මේවා යම් කාලානුක්රමික අනුපිළිවෙලකින් ඉදිරිපත් කර ඇති සංඛ්යාන දර්ශකවල අගයන් වේ.
සෑම කාල මාලාවක්ම සංරචක දෙකක් අඩංගු වේ:
1) කාල සීමාවන් (අවුරුදු, කාර්තු, මාස, දින හෝ දින) දර්ශක;
2) ශ්රේණියේ මට්ටම් ලෙස හැඳින්වෙන කාල පරිච්ඡේද සඳහා හෝ අදාළ දිනයන් සඳහා අධ්යයනයට ලක්ව ඇති වස්තුව සංලක්ෂිත දර්ශක.
මාලාවේ මට්ටම් ප්රකාශිත වේනිරපේක්ෂ සහ සාමාන්ය හෝ සාපේක්ෂ අගයන් දෙකම. දර්ශකවල ස්වභාවය අනුව, නිරපේක්ෂ, සාපේක්ෂ සහ සාමාන්ය අගයන්හි ගතික ශ්රේණි ගොඩනගා ඇත. සාපේක්ෂ සහ සාමාන්ය අගයන්හි ගතික ශ්රේණි ගොඩනගා ඇත්තේ නිරපේක්ෂ අගයන්හි ව්යුත්පන්න ශ්රේණියේ පදනම මත ය. ගතිකයේ අන්තරාලය සහ මොහොත ශ්රේණි ඇත.
ගතික විරාම මාලාවනිශ්චිත කාල පරිච්ඡේද සඳහා දර්ශකවල අගයන් අඩංගු වේ. විරාම ශ්රේණියේ දී, මට්ටම් සාරාංශ කළ හැකි අතර, දිගු කාලයක් සඳහා සංසිද්ධියේ පරිමාව ලබා ගැනීම හෝ ඊනියා සමුච්චිත එකතු කිරීම් ලබා ගත හැකිය.
ගතික මොහොත මාලාවනිශ්චිත වේලාවක (වේලාවේ දිනය) දර්ශකවල අගයන් පිළිබිඹු කරයි. මොහොත ශ්රේණියේ දී, පර්යේෂකයා උනන්දුවක් දක්වන්නේ සංසිද්ධිවල වෙනස ගැන පමණක් වන අතර, මෙහි මට්ටම්වල එකතුවට සැබෑ අන්තර්ගතයක් නොමැති බැවින්, යම් යම් දිනයන් අතර ශ්රේණියේ මට්ටමේ වෙනස පිළිබිඹු කරයි. සමුච්චිත එකතුව මෙහි ගණනය නොකෙරේ.
ගතික ශ්රේණිවල නිවැරදි ඉදිකිරීම සඳහා වඩාත්ම වැදගත් කොන්දේසිය වන්නේ විවිධ කාල පරිච්ඡේදවලට අදාළ ශ්රේණිවල මට්ටම්වල සංසන්දනය කිරීමයි. මට්ටම් සමජාතීය ප්රමාණවලින් ඉදිරිපත් කළ යුතුය, සංසිද්ධියේ විවිධ කොටස් ආවරණය කිරීමේ එකම සම්පූර්ණත්වය තිබිය යුතුය.
වෙතසැබෑ ගතිකත්වය විකෘති කිරීම වළක්වා ගැනීම සඳහා, කාල ශ්රේණියේ සංඛ්යානමය විශ්ලේෂණයට පූර්වගාමී වන සංඛ්යාන අධ්යයනයේ (කාල මාලාව වසා දැමීම) මූලික ගණනය කිරීම් සිදු කරනු ලැබේ. කාල ශ්රේණිය වැසීම යනු ශ්රේණි දෙකක් හෝ වැඩි ගණනක් එක් ශ්රේණියකට එකතු කිරීම ලෙස වටහාගෙන ඇති අතර, ඒවායේ මට්ටම් විවිධ ක්රමවේදයන්ට අනුව ගණනය කරනු ලැබේ හෝ භෞමික මායිම් වලට අනුරූප නොවේ. ගතික ශ්රේණිය වසා දැමීමෙන් ගතික ශ්රේණියේ නිරපේක්ෂ මට්ටම් පොදු පදනමකට අඩු කිරීම ද ගම්ය විය හැකි අතර එමඟින් ගතික ශ්රේණියේ මට්ටම්වල නොගැලපීම ඉවත් කරයි.
කාල ශ්රේණි, සංගුණක, වර්ධන සහ වර්ධන අනුපාත සංසන්දනය කිරීමේ සංකල්පය.
ගතික මාලාව- මේවා කාලයාගේ ඇවෑමෙන් ස්වාභාවික හා සමාජ සංසිද්ධිවල වර්ධනය සංලක්ෂිත සංඛ්යානමය දර්ශක මාලාවකි. රුසියාවේ රාජ්ය සංඛ්යාලේඛන කමිටුව විසින් ප්රකාශයට පත් කරන ලද සංඛ්යාන එකතුවෙහි වගු ආකාරයෙන් කාල ශ්රේණි විශාල ප්රමාණයක් අඩංගු වේ. ගතික ශ්රේණි මගින් අධ්යයනය කරන ලද සංසිද්ධිවල වර්ධනයේ රටා හෙළිදරව් කිරීමට ඉඩ සලසයි.
කාල ශ්රේණියේ දර්ශක වර්ග දෙකක් අඩංගු වේ. කාල දර්ශක(වසර, කාර්තු, මාස, ආදිය) හෝ කාලය තුළ ලකුණු (වසර ආරම්භයේ දී, එක් එක් මාසය ආරම්භයේ දී, ආදිය). පේළි මට්ටමේ දර්ශක. කාල ශ්රේණියේ මට්ටම්වල දර්ශක නිරපේක්ෂ අගයන් (ටොන් හෝ රූබල් වලින් නිෂ්පාදනයක් නිෂ්පාදනය කිරීම), සාපේක්ෂ අගයන් (නාගරික ජනගහනයේ කොටස% වලින්) සහ සාමාන්ය අගයන් (කර්මාන්ත සේවකයින්ගේ සාමාන්ය වැටුප්) වලින් ප්රකාශ කළ හැකිය. වසර, ආදිය). වගු ආකාරයෙන්, කාල ශ්රේණියේ තීරු දෙකක් හෝ පේළි දෙකක් අඩංගු වේ.
කාල ශ්රේණියේ නිවැරදි ගොඩනැගීම අවශ්යතා ගණනාවක් සපුරාලීම ඇතුළත් වේ:
- ගතික ශ්රේණියක සියලුම දර්ශක විද්යාත්මකව සනාථ කළ යුතු, විශ්වාසදායක විය යුතුය;
- ගතික ශ්රේණියක දර්ශක කාලානුරූපව සැසඳිය යුතුය, i.e. එකම කාල පරිච්ඡේද සඳහා හෝ එකම දිනවලදී ගණනය කළ යුතුය;
- ගතිකත්වයන් ගණනාවක දර්ශක භූමිය පුරා සැසඳිය යුතුය;
- ගතික ශ්රේණියක දර්ශක අන්තර්ගතයේ සැසඳිය යුතුය, i.e. එකම ක්රමවේදයකට අනුව ගණනය කරනු ලැබේ;
- ගතික මාලාවක දර්ශක සලකා බලන ගොවිපල පරාසය හරහා සැසඳිය යුතුය. ගතික ශ්රේණියක සියලුම දර්ශක එකම මිනුම් ඒකකවල ලබා දිය යුතුය.
සංඛ්යාන දර්ශකයම් කාල පරිච්ඡේදයක් තුළ අධ්යයනයට ලක්වන ක්රියාවලියේ ප්රතිඵල හෝ අධ්යයනයට ලක්ව ඇති සංසිද්ධි තත්ත්වය යම් නිශ්චිත අවස්ථාවකදී සංලක්ෂිත කළ හැක, i.e. දර්ශක අන්තරාලය (ආවර්තිතා) සහ ක්ෂණික විය හැක. ඒ අනුව, මුලින් ගතික ශ්රේණිය අන්තරය හෝ මොහොත විය හැකිය. ගතිකයේ මොහොත ශ්රේණිය, අනෙක් අතට, සමාන හා අසමාන කාල පරතරයන් සමඟ විය හැකිය.
ගතිකයේ ආරම්භක ශ්රේණිය සාමාන්ය අගයන් මාලාවක් සහ සාපේක්ෂ අගයන් මාලාවක් (දාමය සහ පාදය) බවට පරිවර්තනය කළ හැකිය. එවැනි කාල ශ්රේණි ව්යුත්පන්න කාල ශ්රේණි ලෙස හැඳින්වේ.
ගතික ශ්රේණියේ සාමාන්ය මට්ටම ගණනය කිරීමේ ක්රමය ගතික මාලාවේ වර්ගය නිසා වෙනස් වේ. උදාහරණ භාවිතා කරමින්, සාමාන්ය මට්ටම ගණනය කිරීම සඳහා කාල ශ්රේණි සහ සූත්ර වර්ග සලකා බලන්න.
නිරපේක්ෂ වාසි (Δy) පෙර මට්ටමට සාපේක්ෂව (තීරුව 3. - දාම නිරපේක්ෂ වර්ධක) හෝ ආරම්භක මට්ටමට සාපේක්ෂව (තීරුව 4. - මූලික නිරපේක්ෂ වර්ධක) ශ්රේණියේ පසු මට්ටම ඒකක කීයක් වෙනස් වී ඇත්ද යන්න පෙන්වන්න. ගණනය කිරීමේ සූත්ර පහත පරිදි ලිවිය හැකිය:

ශ්රේණියේ නිරපේක්ෂ අගයන් අඩුවීමත් සමඟ, පිළිවෙලින් "අඩුවීමක්", "අඩුවීමක්" සිදුවනු ඇත.
නිරපේක්ෂ වර්ධනයේ දර්ශක පෙන්නුම් කරන්නේ, උදාහරණයක් ලෙස, 1998 දී "A" නිෂ්පාදනයේ නිෂ්පාදනය 1997 ට සාපේක්ෂව ටොන් 4,000 කින් සහ 1994 ට සාපේක්ෂව ටොන් 34,000 කින් වැඩි වූ බවයි. වෙනත් වසර සඳහා, වගුව බලන්න. ග්රෑම් 11.5 3 සහ 4.
වර්ධන සාධකයශ්රේණියේ මට්ටම පෙර එකට සාපේක්ෂව (5 තීරුව - දාම වර්ධනය හෝ පරිහානිය සාධක) හෝ ආරම්භක මට්ටමට සාපේක්ෂව (6 තීරුව - මූලික වර්ධන හෝ පරිහානිය සාධක) කොපමණ වාර ගණනක් වෙනස් වී ඇත්දැයි පෙන්වයි. ගණනය කිරීමේ සූත්ර පහත පරිදි ලිවිය හැකිය:

වර්ධන අනුපාතශ්රේණියේ මීළඟ මට්ටම පෙර පැවති මට්ටමට (තීරු 7 - දාම වර්ධන අනුපාත) හෝ ආරම්භක මට්ටමට (8 තීරුව - මූලික වර්ධන අනුපාත) සසඳන විට සියයට කීයක් පෙන්වන්න. ගණනය කිරීමේ සූත්ර පහත පරිදි ලිවිය හැකිය:

උදාහරණයක් ලෙස, 1997 දී, 1996 ට සාපේක්ෂව "A" නිෂ්පාදනයේ නිෂ්පාදන පරිමාව 105.5% ක් විය (
වර්ධන වේගයවාර්තාකරණ කාලපරිච්ඡේදයේ මට්ටම පෙර එකට සාපේක්ෂව (තීරුව 9 - දාම වර්ධන අනුපාත) හෝ ආරම්භක මට්ටමට සාපේක්ෂව (තීරුව 10 - මූලික වර්ධන අනුපාත) සියයට කීයක් වැඩි වී ඇත්දැයි පෙන්වන්න. ගණනය කිරීමේ සූත්ර පහත පරිදි ලිවිය හැකිය:
T pr \u003d T p - 100% හෝ T pr \u003d නිරපේක්ෂ වැඩි වීම / පෙර කාල සීමාවේ මට්ටම * 100%
උදාහරණයක් ලෙස, 1995 ට සාපේක්ෂව 1996 දී "A" නිෂ්පාදනය 3.8% (103.8% - 100%) හෝ (8:210) x 100% කින් සහ 1994 ට සාපේක්ෂව - 9% කින් ( 109% - 100%).
ශ්රේණියේ නිරපේක්ෂ මට්ටම් අඩු වුවහොත්, එම අනුපාතය 100% ට වඩා අඩු වනු ඇති අතර, ඒ අනුව, පහත වැටීමේ අනුපාතයක් (අඩු ලකුණක් සහිත වර්ධන වේගය) ඇත.
නිරපේක්ෂ අගය 1% වැඩි වීම(11 තීරුව) පෙර කාල පරිච්ඡේදයේ මට්ටම 1% කින් වැඩි වීම සඳහා දී ඇති කාල සීමාව තුළ ඒකක කීයක් නිෂ්පාදනය කළ යුතුද යන්න පෙන්වයි. අපගේ උදාහරණයේ දී, 1995 දී ටොන් 2.0 දහසක් නිෂ්පාදනය කිරීමට අවශ්ය වූ අතර, 1998 දී - ටොන් 2.3 දහසක්, i.e. වඩා විශාලයි.
1% වර්ධනයේ නිරපේක්ෂ අගයේ විශාලත්වය තීරණය කිරීමට ක්රම දෙකක් තිබේ:
පෙර කාල පරිච්ඡේදයේ මට්ටම 100 න් බෙදන්න;
නිරපේක්ෂ දාම වර්ධන අනුපාත අනුරූප දාම වර්ධන අනුපාතයන් මගින් බෙදන්න.
නිරපේක්ෂ අගය 1% වැඩිවීම = 
ගතිකත්වයේ දී, විශේෂයෙන් දිගු කාලයක් පුරා, එක් එක් ප්රතිශතයේ වැඩිවීමේ හෝ අඩුවීමේ අන්තර්ගතය සමඟ ඒකාබද්ධව වර්ධන වේගය විශ්ලේෂණය කිරීම වැදගත් වේ.
කාල ශ්රේණි විශ්ලේෂණය කිරීම සඳහා සලකා බලන ලද ක්රමවේදය කාල ශ්රේණි සඳහා යන දෙකටම අදාළ වන බව සලකන්න, ඒවායේ මට්ටම් නිරපේක්ෂ අගයන් (t, රූබල් දහසක්, සේවක සංඛ්යාව, ආදිය) සහ කාල ශ්රේණි සඳහා, මට්ටම් ඒවා සාපේක්ෂ දර්ශක වලින් ප්රකාශ වේ (සීතල %, ගල් අඟුරු වල අළු අන්තර්ගතය, ආදිය) හෝ සාමාන්ය අගයන් (c/ha හි සාමාන්ය අස්වැන්න, සාමාන්ය වැටුප්, ආදිය).
පෙර හෝ ආරම්භක මට්ටමට සාපේක්ෂව එක් එක් වර්ෂය සඳහා ගණනය කරන ලද සලකා බැලූ විශ්ලේෂණ දර්ශක සමඟ, කාල ශ්රේණිය විශ්ලේෂණය කිරීමේදී, කාල සීමාව සඳහා සාමාන්ය විශ්ලේෂණ දර්ශක ගණනය කිරීම අවශ්ය වේ: ශ්රේණියේ සාමාන්ය මට්ටම, සාමාන්ය වාර්ෂික නිරපේක්ෂ වැඩි වීම (අඩු වීම) සහ සාමාන්ය වාර්ෂික වර්ධන වේගය සහ වර්ධන වේගය.
ගතික ශ්රේණියක සාමාන්ය මට්ටම ගණනය කිරීමේ ක්රම ඉහත සාකච්ඡා කරන ලදී. අප සලකා බලන ගතික විරාම ශ්රේණියේ දී, ශ්රේණියේ සාමාන්ය මට්ටම ගණනය කරනු ලබන්නේ ගණිත මධ්යන්ය සරල සූත්රයෙනි:
1994-1998 සඳහා නිෂ්පාදනයේ සාමාන්ය වාර්ෂික නිමැවුම. ටොන් 218.4 දහසක් විය.
සාමාන්ය වාර්ෂික නිරපේක්ෂ වැඩිවීම සරල අංක ගණිත මධ්යන්යයේ සූත්රය මගින් ද ගණනය කෙරේ:
වාර්ෂික නිරපේක්ෂ වර්ධක වසර ගණනාවක් පුරා ටොන් 4 සිට 12 දහසක් දක්වා වෙනස් විය (බලන්න gr. 3), සහ 1995 - 1998 කාලය සඳහා නිෂ්පාදනයේ සාමාන්ය වාර්ෂික වැඩිවීම. ටොන් 8.5 දහසක් විය.
සාමාන්ය වර්ධන වේගය සහ සාමාන්ය වර්ධන වේගය ගණනය කිරීම සඳහා ක්රම වඩාත් සවිස්තරාත්මක සලකා බැලීම අවශ්ය වේ. වගුවේ දක්වා ඇති ශ්රේණි මට්ටමේ වාර්ෂික දර්ශකවල උදාහරණයෙන් ඒවා සලකා බලමු.
ගතික පරාසයේ මැද මට්ටම.
ගතික ශ්රේණි (හෝ කාල ශ්රේණි)- මේවා අනුක්රමික අවස්ථා හෝ කාල පරිච්ඡේදවල (එනම් කාලානුක්රමික අනුපිළිවෙලට සකස් කර ඇති) යම් සංඛ්යානමය දර්ශකයක සංඛ්යාත්මක අගයන් වේ.
ගතික ශ්රේණියක් සෑදෙන විශේෂිත සංඛ්යාන දර්ශකයක සංඛ්යාත්මක අගයන් ලෙස හැඳින්වේ. අංකයක මට්ටම්සහ සාමාන්යයෙන් අක්ෂරයෙන් දැක්වේ y. මාලාවේ පළමු සාමාජිකයා y 1ආරම්භක හෝ මූලික රේඛාව, සහ අන්තිම y n - අවසාන. මට්ටම් යොමු කරන අවස්ථා හෝ කාල පරිච්ඡේද මගින් දක්වනු ලැබේ ටී.
ගතික ශ්රේණි, රීතියක් ලෙස, වගුවක් හෝ ප්රස්ථාරයක් ආකාරයෙන් ඉදිරිපත් කර ඇති අතර, x-අක්ෂය ඔස්සේ කාල පරිමාණයක් ගොඩනගා ඇත. ටී, සහ ඕඩිනේට් දිගේ - ශ්රේණියේ මට්ටම්වල පරිමාණය y.
ගතික ශ්රේණියක සාමාන්ය දර්ශක
ගතිකයේ සෑම මාලාවක්ම නිශ්චිත කට්ටලයක් ලෙස සැලකිය හැකිය nසාමාන්යයන් ලෙස සාරාංශගත කළ හැකි කාලය වෙනස් වන දර්ශක. විවිධ කාලවලදී, විවිධ රටවල, එක් හෝ තවත් දර්ශකයක වෙනස්කම් සංසන්දනය කිරීමේදී එවැනි සාමාන්ය (සාමාන්ය) දර්ශක විශේෂයෙන් අවශ්ය වේ.
ගතික ශ්රේණියක සාමාන්යකරණය වූ ලක්ෂණයක් විය හැක්කේ, ප්රථමයෙන්, සාමාන්ය පේළි මට්ටම. සාමාන්ය මට්ටම ගණනය කිරීමේ ක්රමය රඳා පවතින්නේ එය මොහොත ශ්රේණියක් ද නැතහොත් විරාම (කාලසීමාව) ශ්රේණියක් ද යන්න මතය.
කවදා ද පරතරයශ්රේණිය, එහි සාමාන්ය මට්ටම තීරණය වන්නේ ශ්රේණියේ මට්ටම්වල සරල අංක ගණිත මධ්යන්යයක සූත්රයෙනි, i.e.
=
තිබේ නම් මොහොතපේළිය අඩංගු nමට්ටම් ( y1, y2, ..., yn) දිනයන් (කාල ලක්ෂ්ය) අතර සමාන කාල පරතරයන් සහිතව, එවැනි ශ්රේණියක් සාමාන්ය අගයන් මාලාවක් බවට පහසුවෙන් පරිවර්තනය කළ හැකිය. ඒ අතරම, එක් එක් කාල පරිච්ඡේදයේ ආරම්භයේ දී දර්ශකය (මට්ටම) පෙර කාල සීමාව අවසානයේ දී එකවරම දර්ශකය වේ. එවිට එක් එක් කාල සීමාව සඳහා දර්ශකයේ සාමාන්ය අගය (දින අතර පරතරය) අගයන්හි අර්ධ එකතුවක් ලෙස ගණනය කළ හැක. හිදීකාල පරිච්ඡේදයේ ආරම්භයේ සහ අවසානයේ, i.e. කෙසේද . එවැනි සාමාන්ය සංඛ්යාවක් වනු ඇත. කලින් සඳහන් කළ පරිදි, සාමාන්ය ශ්රේණි සඳහා, සාමාන්ය මට්ටම ගණනය කරනු ලබන්නේ අංක ගණිත සාමාන්යයෙන් ය.
එබැවින්, අපට ලිවිය හැකිය: .
.
සංඛ්යාංකය පරිවර්තනය කිරීමෙන් පසු, අපට ලැබෙන්නේ: ,
,
කොහෙද Y1හා Yn- මාලාවේ පළමු සහ අවසාන මට්ටම්; යී- අතරමැදි මට්ටම්.
මෙම සාමාන්යය සංඛ්යාලේඛනවල හඳුන්වන්නේ සාමාන්ය කාලානුක්රමිකමොහොත මාලාව සඳහා. කාලයත් සමඟ වෙනස් වන දර්ශක වලින් ගණනය කර ඇති බැවින් ඇයට මෙම නම ලැබුණේ "cronos" (කාලය, lat.) යන වචනයෙනි.
අසමාන අවස්ථාවකදින අතර කාල පරතරයන්, මොහොත ශ්රේණියේ කාලානුක්රමික සාමාන්යය, දින අතර ඇති දුර (කාල පරතරයන්) මගින් බර කරන ලද එක් එක් අවස්ථාවන් යුගල සඳහා මට්ටම්වල සාමාන්ය අගයන්හි අංක ගණිත සාමාන්යය ලෙස ගණනය කළ හැකිය, i.e.  .
.
මේ අවස්ථාවේ දීදිනයන් අතර කාල පරතරයන් තුළ මට්ටම් විවිධ අගයන් ලබා ගත් බව උපකල්පනය කර ඇති අතර, අපි දන්නා දෙකකින් ( යිහා yi+1) අපි සාමාන්යයන් තීරණය කරමු, ඉන් පසුව අපි සමස්ත විශ්ලේෂණ කාලය සඳහා සමස්ත සාමාන්යය ගණනය කරමු.
එය එක් එක් අගය උපකල්පනය කරන්නේ නම් යිමීලඟ තෙක් නොවෙනස්ව පවතී (i+ 1)-
th moment, i.e. මට්ටම්වල වෙනස් වීමේ නිශ්චිත දිනය දන්නා අතර, බර අංක ගණිත මධ්යන්ය සූත්රය භාවිතයෙන් ගණනය කිරීම සිදු කළ හැකිය:
,
මට්ටම නොවෙනස්ව පැවති කාලය කොහිද?
ගතික ශ්රේණියේ සාමාන්ය මට්ටමට අමතරව, අනෙකුත් සාමාන්ය දර්ශක ද ගණනය කරනු ලැබේ - ශ්රේණියේ මට්ටම්වල සාමාන්ය වෙනසක් (මූලික සහ දාම ක්රම), වෙනස් වීමේ සාමාන්ය අනුපාතය.
මූලික අර්ථය නිරපේක්ෂ වෙනසක්වෙනස්කම් ගණනින් බෙදූ අවසාන මූලික නිරපේක්ෂ වෙනසෙහි ප්රතිශතය වේ. එනම්
දාමය යනු නිරපේක්ෂ වෙනසක් යන්නයි ශ්රේණියක මට්ටම් යනු සියලු දාම නිරපේක්ෂ වෙනස්කම්වල එකතුව වෙනස්කම් ගණනින් බෙදීමේ ප්රමාණයයි, i.e.
සාමාන්ය නිරපේක්ෂ වෙනස්කම්වල සංඥාව මගින්, සංසිද්ධියෙහි වෙනස් වීමේ ස්වභාවය ද සාමාන්යයෙන් විනිශ්චය කරනු ලැබේ: වර්ධනය, පරිහානිය හෝ ස්ථාවරත්වය.
මූලික සහ දාම නිරපේක්ෂ වෙනස්කම් පාලනය කිරීම සඳහා රීතියෙන්, මූලික සහ දාම සාමාන්ය වෙනස්කම් සමාන විය යුතු බව අනුගමනය කරයි.
සාමාන්ය නිරපේක්ෂ වෙනසක් සමඟින්, සාමාන්ය ඥාතියෙකු ද මූලික සහ දාම ක්රම භාවිතයෙන් ගණනය කෙරේ.
මූලික සාමාන්ය සාපේක්ෂ වෙනසක්සූත්රය මගින් තීරණය කරනු ලැබේ:
දාමය යනු සාපේක්ෂ වෙනස් වීමයිසූත්රය මගින් තීරණය කරනු ලැබේ:
ස්වාභාවිකවම, මූලික හා දාම සාමාන්ය සාපේක්ෂ වෙනස්කම් සමාන විය යුතු අතර, ඒවා 1 හි නිර්ණායක අගය සමඟ සංසන්දනය කිරීමෙන්, සාමාන්යයෙන් සංසිද්ධියේ වෙනස් වීමේ ස්වභාවය පිළිබඳව නිගමනයකට එළඹේ: වර්ධනය, පහත වැටීම හෝ ස්ථාවරත්වය.
පාදයේ හෝ දාමයේ සාමාන්ය සාපේක්ෂ වෙනස් වීමෙන් 1 අඩු කිරීමෙන්, අනුරූප වේ වෙනස් වීමේ සාමාන්ය අනුපාතය, මෙම ගතික ශ්රේණියෙන් පිළිබිඹු වන අධ්යයනයට භාජනය වන සංසිද්ධියේ වෙනස්වීමේ ස්වභාවය ද විනිශ්චය කළ හැකි ලකුණක් මගින්.
සෘතුමය උච්චාවචනයන් සහ සෘතුමය දර්ශක.
සෘතුමය උච්චාවචනයන් ස්ථායී අන්තර්-වාර්ෂික උච්චාවචනයන් වේ.
උපරිම බලපෑම ලබා ගැනීම සඳහා කළමනාකරණය කිරීමේ මූලික මූලධර්මය වන්නේ ආදායම උපරිම කිරීම සහ පිරිවැය අවම කිරීමයි. සෘතුමය උච්චාවචනයන් අධ්යයනය කිරීමෙන්, වසරේ එක් එක් මට්ටම්වල උපරිම සමීකරණයේ ගැටළුව විසඳනු ලැබේ.
සෘතුමය උච්චාවචනයන් අධ්යයනය කරන විට, අන්තර් සම්බන්ධිත කාර්යයන් දෙකක් විසඳනු ලැබේ:
1. අන්තර්-වාර්ෂික ගතිකත්වයේ සංසිද්ධිය වර්ධනය කිරීමේ විශේෂතා හඳුනා ගැනීම;
2. සෘතුමය තරංග ආකෘතියක් ඉදිකිරීම සමඟ සෘතුමය උච්චාවචනයන් මැනීම;
සෘතුමය තුර්කිය සාමාන්යයෙන් ගණනය කරනු ලබන්නේ සෘතුමය බව මැනීම සඳහාය. පොදුවේ ගත් කල, ඒවා සංසන්දනය කිරීම සඳහා පදනමක් ලෙස සේවය කරන න්යායික සමීකරණවලට ගතික මාලාවක මුල් සමීකරණවල අනුපාතය අනුව තීරණය වේ.
සෘතුමය උච්චාවචනයන් මත අහඹු අපගමනයන් අධිස්ථාපනය වන බැවින්, ඒවා ඉවත් කිරීම සඳහා සෘතුමය දර්ශක සාමාන්යය වේ.
මෙම අවස්ථාවෙහිදී, වාර්ෂික චක්රයේ එක් එක් කාල පරිච්ඡේදය සඳහා, සාමාන්යකරණය කරන ලද දර්ශක සාමාන්ය සෘතුමය දර්ශක ආකාරයෙන් තීරණය වේ:
සෘතුමය උච්චාවචනයන් පිළිබඳ සාමාන්ය දර්ශක ප්රධාන සංවර්ධන ප්රවණතාවයේ අහඹු අපගමනයන්ගේ බලපෑමෙන් නිදහස් වේ.
ප්රවණතාවයේ ස්වභාවය අනුව, සාමාන්ය සෘතුමය දර්ශකය සඳහා සූත්රය පහත ආකාර ගත හැක:
1.උච්චාරණය කරන ලද ප්රධාන සංවර්ධන ප්රවණතාවක් සහිත අන්තර්-වාර්ෂික ගතිකතා මාලාවක් සඳහා:
2. ඉහළට හෝ පහළට නැඹුරුවක් නොමැති, හෝ නොවැදගත් වන අන්තර්-වාර්ෂික ගතික ශ්රේණි සඳහා:
සාමාන්ය සාමාන්යය කොහිද;
ප්රධාන ප්රවණතාවය විශ්ලේෂණය කිරීමේ ක්රම.
කාලයාගේ ඇවෑමෙන් සංසිද්ධි වර්ධනය වීම ස්වභාවයෙන්ම වෙනස් වන සාධක සහ බලපෑමේ ශක්තිය බලපායි. ඒවායින් සමහරක් අහඹු ස්වභාවයක් ගනී, අනෙක් ඒවා පාහේ නියත බලපෑමක් ඇති අතර ගතිකතා මාලාවේ යම් සංවර්ධන ප්රවණතාවක් සාදයි.
සංඛ්යාලේඛනවල වැදගත් කාර්යයක් වන්නේ විවිධ අහඹු සාධකවල ක්රියාකාරිත්වයෙන් මිදී ගතික ශ්රේණියේ ප්රවණතාවක් හඳුනා ගැනීමයි. මෙම කාර්යය සඳහා කාල ශ්රේණිය සකසනු ලබන්නේ විරාම විශාල කිරීම, චලනය වන සාමාන්යය සහ විශ්ලේෂණාත්මක පෙළගැස්ම යනාදියෙනි.
විරාම රළු කිරීමේ ක්රමයගතික ශ්රේණියක මට්ටම් ඇතුළත් කාල පරිච්ඡේදවල විශාල වීම මත පදනම් වේ, i.e. කුඩා කාල පරිච්ඡේදවලට අදාළ දත්ත විශාල කාල පරිච්ඡේදවල දත්ත සමඟ ප්රතිස්ථාපනය කිරීමයි. මාලාවේ ආරම්භක මට්ටම් කෙටි කාලයක් සඳහා වන විට එය විශේෂයෙන් ඵලදායී වේ. උදාහරණයක් ලෙස, දෛනික සිදුවීම්වලට අදාළ දර්ශක මාලාව සතිපතා, මාසිකව, ආදියට අදාළ ශ්රේණි මගින් ප්රතිස්ථාපනය වේ. මෙය වඩාත් පැහැදිලිව පෙන්වනු ඇත "සංසිද්ධියේ වර්ධනයේ අක්ෂය". සාමාන්යය, විශාල කරන ලද කාල පරතරයන් මත පදනම්ව, ප්රධාන සංවර්ධන ප්රවණතාවයේ දිශාව සහ චරිතය (වර්ධන ත්වරණය හෝ අඩුවීම) හඳුනා ගැනීමට හැකි වේ.
චලනය වන සාමාන්ය ක්රමයපෙර එකට සමාන, නමුත් මෙම අවස්ථාවෙහිදී, සත්ය මට්ටම් අනුක්රමිකව චලනය වන (ස්ලයිඩින්) විශාල කරන ලද විරාම ආවරණය සඳහා ගණනය කරන ලද සාමාන්ය මට්ටම් මගින් ප්රතිස්ථාපනය වේ. එම්පේළි මට්ටම්.
උදාහරණ වශයෙන්පිළිගන්නවා නම් m=3,පසුව, පළමුව, ශ්රේණියේ පළමු මට්ටම් තුනේ සාමාන්යය ගණනය කරනු ලැබේ, පසුව - එකම මට්ටම් ගණනකින්, නමුත් පේළියේ දෙවැන්නෙන් ආරම්භ වේ, පසුව - තුන්වන සිට ආරම්භ වේ. මේ අනුව, සාමාන්යය, ගතික ශ්රේණිය දිගේ "ස්ලයිඩ්" ලෙස, එක් කාල පරිච්ඡේදයක් සඳහා චලනය වේ. සිට ගණනය කර ඇත එම්චලනය වන සාමාන්ය වල සාමාජිකයින් එක් එක් කාල පරතරයේ මැද (මැද) වෙත යොමු වේ.
මෙම ක්රමය අහඹු උච්චාවචනයන් පමණක් ඉවත් කරයි. ශ්රේණියේ සෘතුමය තරංගයක් තිබේ නම්, එය චලනය වන සාමාන්ය ක්රමය මගින් සුමට කිරීමෙන් පසුව පවතිනු ඇත.
විශ්ලේෂණාත්මක පෙළගැස්ම. අහඹු උච්චාවචනයන් ඉවත් කිරීම සහ ප්රවණතාවක් හඳුනා ගැනීම සඳහා, ශ්රේණියේ මට්ටම් විශ්ලේෂණාත්මක සූත්ර (හෝ විශ්ලේෂණාත්මක පෙළගැස්ම) අනුව පෙළගස්වනු ලැබේ. එහි සාරය නම්, යම් සමීකරණයකට අනුව ගණනය කරනු ලබන අනුභූතික (සැබෑ) මට්ටම් න්යායාත්මක ඒවා සමඟ ප්රතිස්ථාපනය කිරීමයි, ප්රවණතාවයේ ගණිතමය ආකෘතියක් ලෙස ගනු ලැබේ, එහිදී න්යායික මට්ටම් කාලයෙහි ශ්රිතයක් ලෙස සැලකේ: . මෙම අවස්ථාවෙහිදී, සෑම තථ්ය මට්ටමක්ම සංරචක දෙකක එකතුවක් ලෙස සලකනු ලැබේ: , ක්රමානුකූල සංරචකයක් වන අතර යම් සමීකරණයකින් ප්රකාශිත වන අතර එය ප්රවණතාවය වටා උච්චාවචනයන් ඇති කරන අහඹු විචල්යයකි.
විශ්ලේෂණාත්මක එකලස් කිරීමේ කාර්යය පහත පරිදි වේ:
1. අධ්යයනයට භාජනය වන දර්ශකයේ සංවර්ධන ප්රවණතාවය වඩාත් ප්රමාණවත් ලෙස පිළිබිඹු කළ හැකි උපකල්පිත ශ්රිතයේ වර්ගය සත්ය දත්ත මත පදනම්ව තීරණය කිරීම.
2. ආනුභවික දත්ත වලින් නිශ්චිත ශ්රිතයේ (සමීකරණයේ) පරාමිතීන් සොයා ගැනීම
3. න්යායික (මට්ටම් සහිත) මට්ටම්වල සොයාගත් සමීකරණය අනුව ගණනය කිරීම.
කිසියම් කාර්යයක් තෝරාගැනීම, රීතියක් ලෙස, ආනුභවික දත්තවල චිත්රක නිරූපණයක් මත සිදු කරනු ලැබේ.
ආකෘති යනු ප්රතිගාමී සමීකරණ වන අතර ඒවායේ පරාමිතීන් අවම වර්ග ක්රමය මගින් ගණනය කෙරේ
පහත දැක්වෙන්නේ කාල ශ්රේණි මට්ටම් කිරීම සඳහා බහුලව භාවිතා වන ප්රතිගාමී සමීකරණ, ඒවා පරාවර්තනය කිරීමට වඩාත් සුදුසු සංවර්ධන ප්රවණතා පෙන්නුම් කරයි.
ඉහත සමීකරණවල පරාමිතීන් සොයා ගැනීම සඳහා, විශේෂ ඇල්ගොරිතම සහ පරිගණක වැඩසටහන් තිබේ. විශේෂයෙන්, සරල රේඛාවක සමීකරණයේ පරාමිතීන් සොයා ගැනීමට, පහත ඇල්ගොරිතම භාවිතා කළ හැකිය:

St = 0 ලැබෙන පරිදි කාල පරිච්ඡේද හෝ අවස්ථා අංකනය කර ඇත්නම්, ඉහත ඇල්ගොරිතම සැලකිය යුතු ලෙස සරල කර ඒවා බවට හැරෙනු ඇත.

ප්රස්ථාරයේ පෙළගැස්වූ මට්ටම් මෙම ගතික ශ්රේණියේ සත්ය මට්ටම්වලින් ආසන්නතම දුරින් ගමන් කරන එක් සරල රේඛාවක් මත පිහිටයි. වර්ග අපගමනයන්හි එකතුව අහඹු සාධකවල බලපෑම පිළිබිඹු කිරීමකි.
එහි ආධාරයෙන්, අපි සමීකරණයේ සාමාන්ය (සම්මත) දෝෂය ගණනය කරමු:

මෙහි n යනු නිරීක්ෂණ ගණන වන අතර, m යනු සමීකරණයේ ඇති පරාමිති ගණන (අපට ඒවායින් දෙකක් ඇත - b 1 සහ b 0).
ප්රධාන ප්රවණතාවය (ප්රවණතාවය) මඟින් ක්රමානුකූල සාධක ගතික ශ්රේණියක මට්ටම්වලට බලපාන ආකාරය පෙන්නුම් කරයි, සහ ප්රවණතාවය වටා ඇති මට්ටම්වල උච්චාවචනය () අවශේෂ සාධකවල බලපෑම පිළිබඳ මිනුමක් ලෙස ක්රියා කරයි.
භාවිතා කරන කාල ශ්රේණියේ ආකෘතියේ ගුණාත්මකභාවය තක්සේරු කිරීම සඳහා, එය ද භාවිතා වේ ෆිෂර්ගේ එෆ් පරීක්ෂණය. එය විචල්ය දෙකක අනුපාතයයි, එනම් ප්රතිගාමීත්වය නිසා ඇතිවන විචල්යයේ අනුපාතය, i.e. අධ්යයනය කරන ලද සාධකය, අහඹු හේතූන් නිසා ඇතිවන විසරණයට, i.e. අවශේෂ විචලනය:
![]()
විස්තීරණ ආකාරයෙන්, මෙම නිර්ණායකය සඳහා සූත්රය පහත පරිදි නිරූපණය කළ හැකිය:
![]()
මෙහි n යනු නිරීක්ෂණ ගණන, i.e. පේළි මට්ටම් ගණන,
m යනු සමීකරණයේ ඇති පරාමිති ගණන, y යනු ශ්රේණියේ සත්ය මට්ටමයි,
පේළියේ පෙළගැස්වූ මට්ටම, - පේළියේ සාමාන්ය මට්ටම.
අනෙක් අයට වඩා සාර්ථක වන අතර, ආකෘතිය සෑම විටම ප්රමාණවත් තරම් සතුටුදායක නොවිය හැකිය. එය එසේ හඳුනාගත හැක්කේ ඒ සඳහා වන F නිර්ණායකය යම් තීරණාත්මක සීමාවක් ඉක්මවා ගියහොත් පමණි. මෙම මායිම F බෙදාහැරීමේ වගු භාවිතයෙන් සකසා ඇත.
දර්ශකවල සාරය සහ වර්ගීකරණය.
සංඛ්යාලේඛනවල දර්ශක සාපේක්ෂ දර්ශකයක් ලෙස වටහාගෙන ඇති අතර එය කාලය, අවකාශය හෝ ඕනෑම ප්රමිතියකට සාපේක්ෂව සංසිද්ධියක විශාලත්වයේ වෙනස සංලක්ෂිත වේ.
දර්ශක සම්බන්ධතාවයේ ප්රධාන අංගය වන්නේ සුචිගත අගයයි. සුචිගත අගයක් සංඛ්යානමය ජනගහනයක ලකුණක අගය ලෙස වටහාගෙන ඇති අතර, එහි වෙනස අධ්යයනයේ පරමාර්ථය වේ.
දර්ශක ප්රධාන අරමුණු තුනක් ඉටු කරයි:
1) සංකීර්ණ සංසිද්ධියක වෙනස්කම් තක්සේරු කිරීම;
2) සංකීර්ණ සංසිද්ධියක් වෙනස් කිරීම සඳහා තනි සාධකවල බලපෑම තීරණය කිරීම;
3) යම් සංසිද්ධියක විශාලත්වය පසුගිය කාල පරිච්ඡේදයේ විශාලත්වය, වෙනත් භූමියක විශාලත්වය මෙන්ම ප්රමිති, සැලසුම්, පුරෝකථනයන් සමඟ සංසන්දනය කිරීම.
දර්ශක නිර්ණායක 3 කට අනුව වර්ගීකරණය කර ඇත:
2) ජනගහනයේ මූලද්රව්යවල ආවරණ මට්ටම අනුව;
3) සාමාන්ය දර්ශක ගණනය කිරීමේ ක්රම මගින්.
අන්තර්ගතය අනුවසුචිගත අගයන්, දර්ශක ප්රමාණාත්මක (පරිමාමිතික) දර්ශක සහ ගුණාත්මක දර්ශකවල දර්ශකවලට බෙදා ඇත. ප්රමාණාත්මක දර්ශකවල දර්ශක - කාර්මික නිෂ්පාදනයේ භෞතික පරිමාවේ දර්ශක, විකුණුම්වල භෞතික පරිමාව, සංඛ්යාව, ආදිය. ගුණාත්මක දර්ශකවල දර්ශක - මිල, පිරිවැය, ශ්රම ඵලදායිතාව, සාමාන්ය වැටුප්, ආදිය.
ජනගහනයේ ඒකක ආවරණය කිරීමේ මට්ටම අනුව, දර්ශක පන්ති දෙකකට බෙදා ඇත: තනි සහ සාමාන්ය. ඒවා සංලක්ෂිත කිරීම සඳහා, දර්ශක ක්රමය භාවිතා කිරීමේ භාවිතයේදී අනුගමනය කරන ලද පහත සඳහන් සම්මුතීන් අපි හඳුන්වා දෙන්නෙමු:
q- ඕනෑම භාණ්ඩයක ප්රමාණය (පරිමාව). ; ආර්- නිෂ්පාදන ඒකක මිල; z- නිෂ්පාදන ඒකක පිරිවැය; ටී- නිමැවුම් ඒකකයක් නිෂ්පාදනය සඳහා ගත කරන කාලය (ශ්රම තීව්රතාවය) ; w- නිෂ්පාදන නිමැවුම කාලය ඒකකයකට වටිනාකම අනුව; v- කාල ඒකකයකට භෞතික වශයෙන් ප්රතිදානය; ටී- ගත කළ මුළු කාලය හෝ සේවක සංඛ්යාව.
සුචිගත අගයන් අයත් වන්නේ කුමන කාල පරිච්ඡේදයට හෝ වස්තුවටද යන්න වෙන්කර හඳුනා ගැනීම සඳහා, පහළ දකුණේ ඇති අනුරූප සංකේතයට පසුව උපසිරැසි තැබීම සිරිතකි. උදාහරණයක් ලෙස, ගතිකයේ දර්ශකවල, රීතියක් ලෙස, සංසන්දනාත්මක (වත්මන්, වාර්තාකරණ) කාල පරිච්ඡේද සඳහා, උපසිරැසි 1 භාවිතා කරනු ලබන අතර, සංසන්දනය කරන කාල පරිච්ඡේද සඳහා,
තනි දර්ශකසංකීර්ණ සංසිද්ධියක තනි මූලද්රව්යවල වෙනස ගුනාංගීකරනය කිරීමට සේවය කරයි (උදාහරණයක් ලෙස, එක් වර්ගයක නිෂ්පාදනයක නිමැවුම් පරිමාවේ වෙනසක්). ඒවා ගතිකත්වයේ සාපේක්ෂ අගයන්, වගකීම් ඉටු කිරීම, සුචිගත අගයන් සංසන්දනය කිරීම නියෝජනය කරයි.
නිෂ්පාදනයේ භෞතික පරිමාවේ තනි දර්ශකය තීරණය කරනු ලැබේ
විශ්ලේෂණාත්මක දෘෂ්ටි කෝණයකින්, ලබා දී ඇති තනි ගතික දර්ශක වර්ධන සංගුණක (අනුපාත) වලට සමාන වන අතර මූලික එක හා සසඳන විට වත්මන් කාල පරිච්ෙඡ්දය තුළ සුචිගත අගයෙහි වෙනස ගුනාංගීකරනය කරයි, එනම් එය කොපමණ වාරයක් වැඩි වී ඇත්ද (අඩු වී තිබේද යන්න පෙන්වන්න. ) හෝ එය සියයට කීයක් වර්ධනය (අඩු වීම). දර්ශක අගයන් සංගුණක හෝ ප්රතිශත වලින් ප්රකාශ වේ.
සාමාන්ය (සංයුක්ත) දර්ශකයසංකීර්ණ සංසිද්ධියක සියලුම අංගවල වෙනස පිළිබිඹු කරයි.
සමස්ථ දර්ශකයදර්ශකයේ මූලික ස්වරූපය වේ. එහි සංඛ්යාව සහ හරය "සමස්ථ" කට්ටලයක් වන බැවින් එය සමස්ථය ලෙස හැඳින්වේ.
සාමාන්ය දර්ශක, ඒවායේ නිර්වචනය.
සමස්ථ දර්ශක වලට අමතරව, ඒවායේ තවත් ආකාරයක් සංඛ්යා ලේඛනවල භාවිතා වේ - බර සාමාන්ය දර්ශක. පවතින තොරතුරු සාමාන්ය සමස්ත දර්ශකය ගණනය කිරීමට ඉඩ නොදෙන විට ඔවුන්ගේ ගණනය කිරීම සිදු කෙරේ. එබැවින්, මිල පිළිබඳ දත්ත නොමැති නම්, නමුත් වත්මන් කාල සීමාව තුළ නිෂ්පාදනවල පිරිවැය පිළිබඳ තොරතුරු තිබේ නම් සහ එක් එක් නිෂ්පාදනය සඳහා තනි මිල දර්ශක දන්නා නම්, සාමාන්ය මිල දර්ශකය සමස්ථ එකක් ලෙස තීරණය කළ නොහැකිය, නමුත් එය කළ හැකිය. එක් එක් අයගේ සාමාන්යය ලෙස එය ගණනය කිරීමට. එලෙසම, නිෂ්පාදනය කරන ලද තනි නිෂ්පාදන ප්රමාණයන් නොදන්නේ නම්, නමුත් තනි දර්ශක සහ මූලික කාලපරිච්ඡේදයේ නිෂ්පාදන පිරිවැය දන්නේ නම්, නිෂ්පාදන භෞතික පරිමාවේ සමස්ත දර්ශකය බරිත සාමාන්යයක් ලෙස තීරණය කළ හැකිය.
සාමාන්ය දර්ශකය -මෙයතනි දර්ශකවල සාමාන්යයක් ලෙස ගණනය කරන ලද දර්ශකයකි. සමස්ථ දර්ශකය යනු සාමාන්ය දර්ශකයේ මූලික ස්වරූපයයි, එබැවින් සාමාන්ය දර්ශකය සමස්ථ දර්ශකයට සමාන විය යුතුය. සාමාන්ය දර්ශක ගණනය කිරීමේදී, සාමාන්ය ආකාර දෙකක් භාවිතා වේ: අංක ගණිතය සහ ප්රතිමූර්තිය.
තනි දර්ශකවල බර සමස්ථ දර්ශකයේ හරයේ නියමයන් නම්, ගණිත මධ්යන්ය දර්ශකය සමස්ථ දර්ශකයට සමාන වේ. මෙම අවස්ථාවේ දී පමණක් අංක ගණිත මධ්යන්ය සූත්රය මගින් ගණනය කරන ලද දර්ශකයේ අගය සමස්ත දර්ශකයට සමාන වේ.







